基于LSSVM和GA的镍铬合金薄膜制备工艺参数优化

郜冉，武文革，宋丁

中北大学机械工程学院

1 引言

镍铬合金薄膜具有高电阻率与可靠性[1]，因此被广泛应用于传感器上。许多研究人员对Ni-Cr合金薄膜的结构与性能进行了相应的研究[2-4]，发现其性能在薄膜制备过程中受到工艺参数的影响，因此对镍铬合金薄膜制备参数进行优化十分重要。Asafa T.B.等[5]运用灰色田口方法优化了CVD沉积多晶硅薄膜的性能。Li J.等[6]利用CFD和遗传算法对MOCVD制备氧化锌薄膜工艺参数进行研究和优化。Yücel Ersin等[7]采用响应面法对硫化镉薄膜的工艺参数进行了优化。此外，响应曲面法、人工神经网络及粒子群算法等也可优化相关的工艺参数。

由于镍铬合金薄膜性能研究的试验数据样本较少，使用上述方法优化镍铬合金薄膜存在优化精度不高的问题，不能很好适用于本研究。支持向量机由Vapnik V.提出，可以用于非线性回归[8]并具有多种优点，当试验数据量少时，其解总是全局的，易于计算，因此被广泛应用。梁耀东等[9]提出一种改进PSO算法的混合核函数LSSVM模型，实现了大坝水平变形的时间序列预测方法。刘昕玥等[10]建立基于组合核函数的流量预测支持向量机模型，将线性核函数与多项式核函数线性组合，运用改进的自适应遗传算法对组合系数进行寻优。Chen Y.等[11]提出了一种结合径向基(RBF)和基于洛伦兹函数的核函数的新组合核函数，通过LSSVM建立电价预测模型。Tian Zhongda等[12]将高斯核和多项式核混合，利用IFS算法得到了混合核LSSVM的最优参数，建立了预测模型。本文提出基于LSSVM建立工艺参数与镍铬合金薄膜性能间的预测模型，通过遗传算法得到最佳工艺参数，这对分析工艺参数与薄膜性能间的映射关系具有重要意义。

2 镍铬合金薄膜制备工艺的正交试验设计及分析

2.1 试验及结果

本研究利用FJL-560a型磁控与离子束复合溅射沉积系统在304不锈钢基底上沉积溅射Al2O3薄膜，采用SI-500D等离子沉积机沉积Si3N4薄膜，在此基础上通过磁控与离子束复合溅射沉积系统磁控溅射制备沉积镍铬合金薄膜。试验控制功率、压强、基底温度和偏压四个因素，采用四因素四水平正交试验进行16组试验，得到16组样品。利用OLS4100激光共聚焦显微镜测量镍铬合金薄膜的表面粗糙度值，利用P-7台阶仪测量薄膜厚度，获得镍铬合金薄膜的平均沉积速率，试验数据见表1。

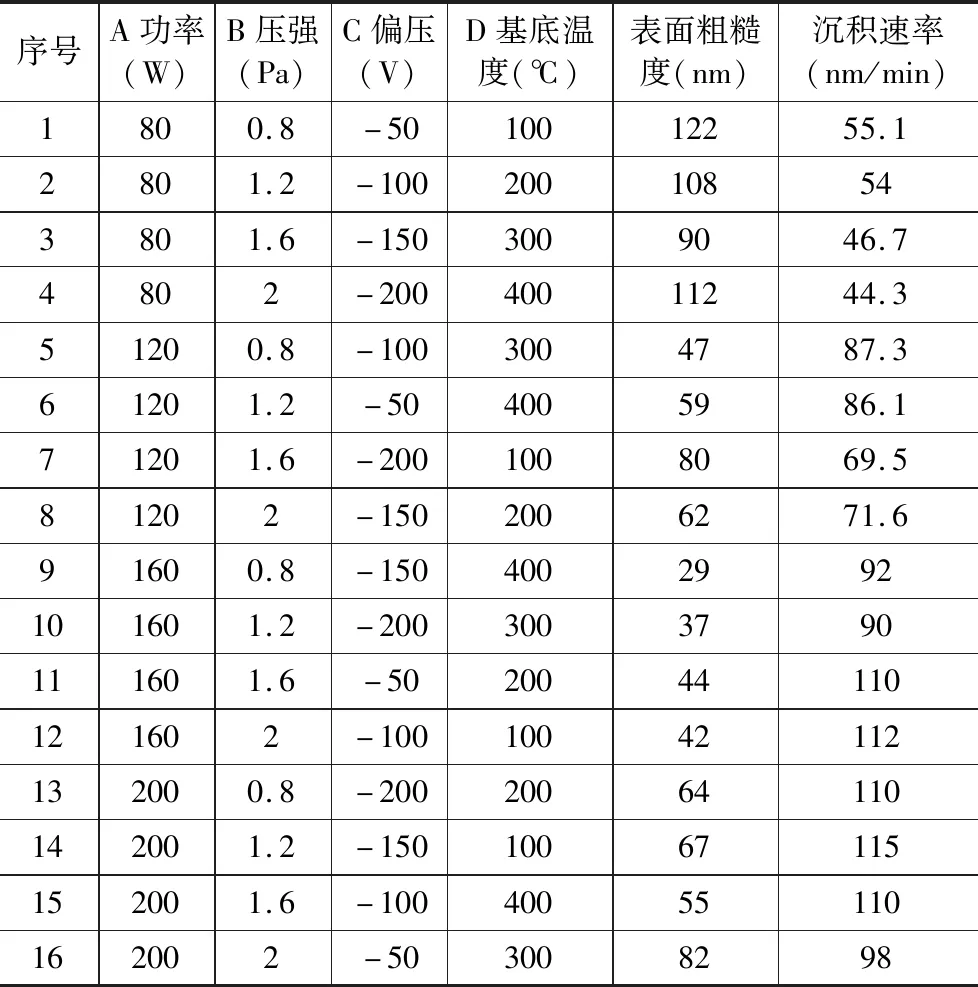
表1 正交试验设计结果

2.2 极差分析

通过极差分析法分析功率、压强、偏压和温度分别对表面粗糙度和电阻率沉积速率的影响，分析四种因素对薄膜性能的影响程度。K1，K2，K3，K4分别为各因素的四个水平对应的试验结果总和；分别表示各水平对应的试验结果平均值。R是极差，即中最大值与最小值的差值。

由表2可知，各因素对表面粗糙度影响按照降序排列为功率、偏压、基底温度和压强。正交试验设计得到的最佳工艺参数为A1B2C1D1，即功率为80W，压强为1.2Pa，偏压为50V，基底温度为100℃。

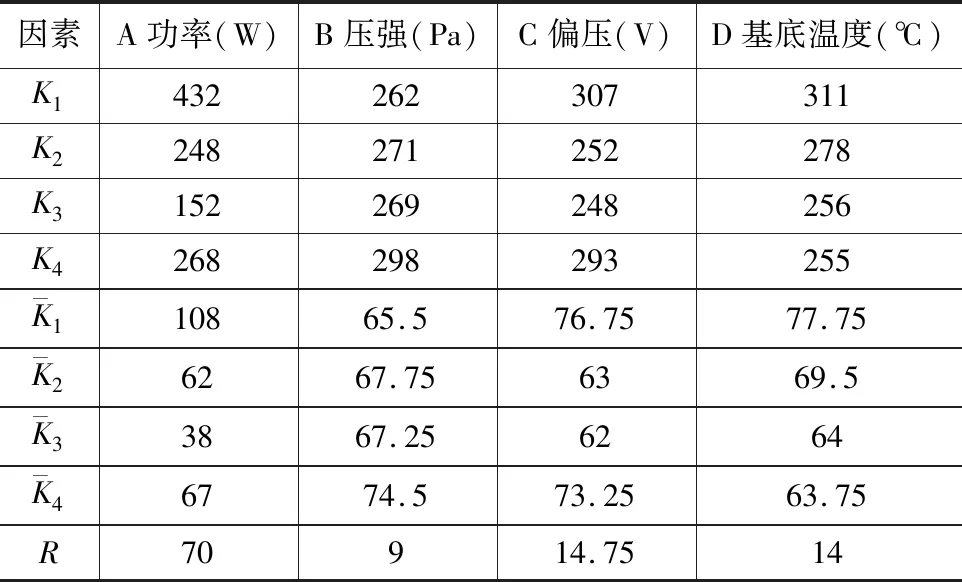
表2 表面粗糙度的极差分析

由表3可得，各因素对沉积速率影响按照降序排列为功率、偏压、基底温度和压强。正交试验设计可得到的最佳工艺参数为A4B2C2D1，即功率为80W，压强为1.2Pa，偏压为50V，基底温度为100℃。

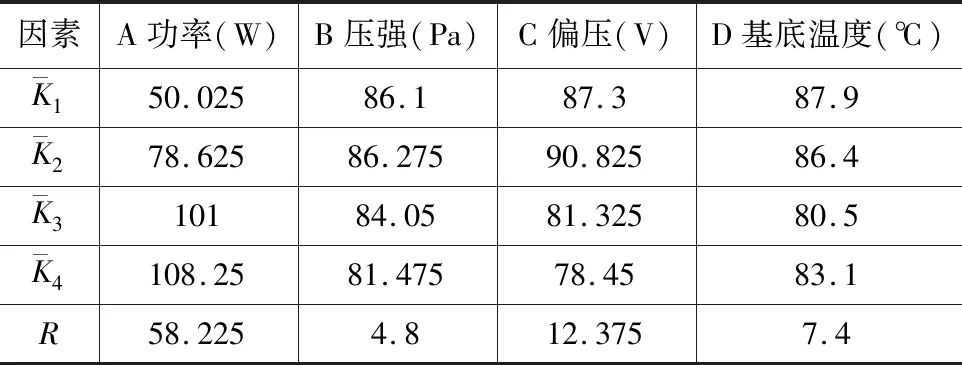
表3 沉积速率的极差分析

极差分析法只能在正交试验基础上得出最佳工艺参数组合，并不能得出某个工艺参数区间内的最佳工艺参数，这对预测薄膜最佳性能有较大影响。因此，本文提出了PSO-LSSVM和GA结合联合工艺参数方法，以此得到某区间内的最佳工艺参数组合。

3 LSSVM和GA联合多工艺参数优化

3.1 多工艺参数优化原理

本文提出了LSSVM和GA联合多工艺参数优化方法获得薄膜的最佳性能，其原理是在正交试验设计结果基础上，利用LSSVM建立功率、压强、偏压和基底温度四种工艺参数对镍铬合金薄膜表征性能的非线性回归函数模型，通过该模型得到非线性回归函数，并进行GA算法寻优。多工艺参数优化流程见图1，其中，采用混合核函数并优化核函数参数对模型建立有着重要作用。

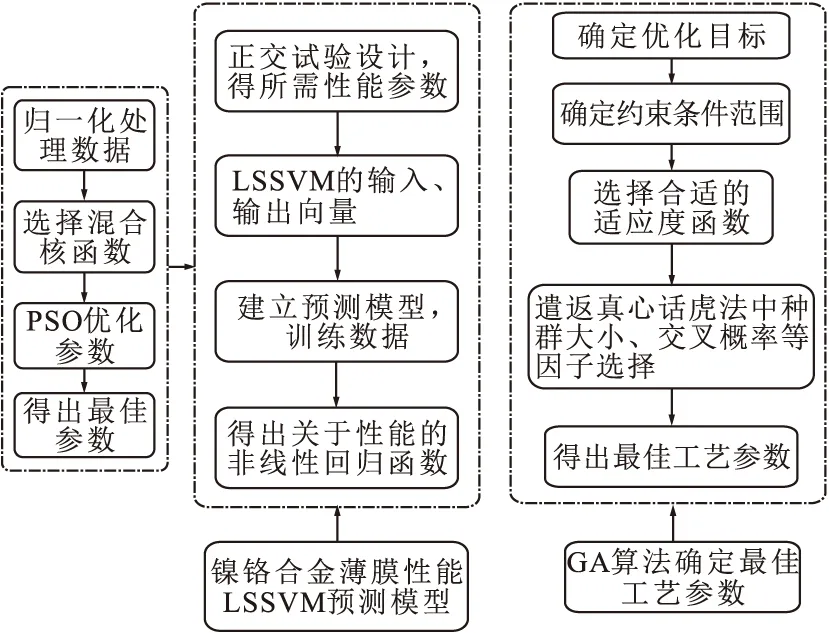
图1 PSO-LSSVM和GA联合多工艺参数优化流程

3.2 建立PSO-LSSVM非线性回归函数模型

选择PSO-LSSVM法建立镍铬合金薄膜的单一性能函数模型，可描述为

(1)

由于四种不同工艺参数的量纲在正交试验中训练数据时会影响算法，造成镍铬合金薄膜模型预测精度不准确，所以对试验数据进行归一化处理，有

x′=[x-min(x)]/[max(x)-min(x)]

(2)

通过式(2)将正交试验数据归一化到[0，1]区间内。

当LSSVM处理试验数据间的关系时，核函数对数据处理能力有着非常重要的作用。混合核函数能够提高模型的预测精度，本文采用高斯与多项式混合的核函数，有

(3)

式中，η为权重因子，η∈[0，1]；γ为惩罚系数，γ∈[0.1，100]；σ2为RBF核宽度，σ∈[0.1，100]；d为多项式核的阶次，d∈{1，2，3，4，5}。

上述四个参数决定镍铬合金薄膜预测模型的精度，本文通过PSO算法对四个参数进行多目标优化，并给出四个参数的取值范围，通过优化得到四个参数值。

均方误差是反映估计量与被估计量之间差异程度的一种度量。选择均方误差(MSE)评估预测模型的性能，通过均方误差可以评估预测模型的准确性，其计算式为

(4)

式中，yi是实验值；是模型的预测值；n为样本数据的数量。

通过MATLAB软件运行程序可以得到如图2所示的输出模型建模结果。表面粗糙度的均方误差为0.0045474，沉积速率的均方误差为0.0047055。最终可以得到功率、压强、基底温度和偏压分别对表面粗糙度、沉积速率的回归函数为

(5)

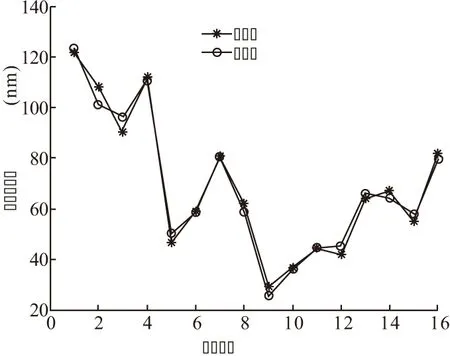
(a)表面粗糙度

3.3 GA算法多工艺参数优化

遗传算法可得出非线性回归函数最优值，本文的优化目标为薄膜表面粗糙度和薄膜沉积速率。以沉积功率、压强、偏压和基底温度四个因素作为遗传算法的输入变量，以薄膜表面粗糙度和薄膜沉积速率作为输出变量，遗传算法中需要选择输入变量的范围为

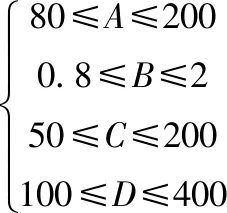
(6)

GA的迭代次数设为50次，种群规模为20，交叉概率为0.6，变异概率为0.01。为获得最小薄膜表面粗糙度和最大沉积速率，在表面粗糙度的遗传算法寻最佳工艺参数时应选择LSSVM所得回归函数为适应度函数，可表示为

(7)

沉积速率寻最佳工艺参数时，选择LSSVM所得回归函数的倒数为适应度函数，可表示为

(8)

经过不断选择、交叉、变异迭代和进化，最终分别得到薄膜表面粗糙度和薄膜沉积速率倒数的最小值，镍铬合金薄膜表面粗糙度的最佳工艺参数为功率172W，压强0.8Pa，偏压 129V，基底温度 400℃，对应的表面粗糙度为23.7nm；沉积速率的最佳工艺参数为功率200W，压强为1.2Pa，偏压为50V，基底温度100℃，对应的沉积速率为126.6nm/min；适应度函数收敛情况如图3所示。

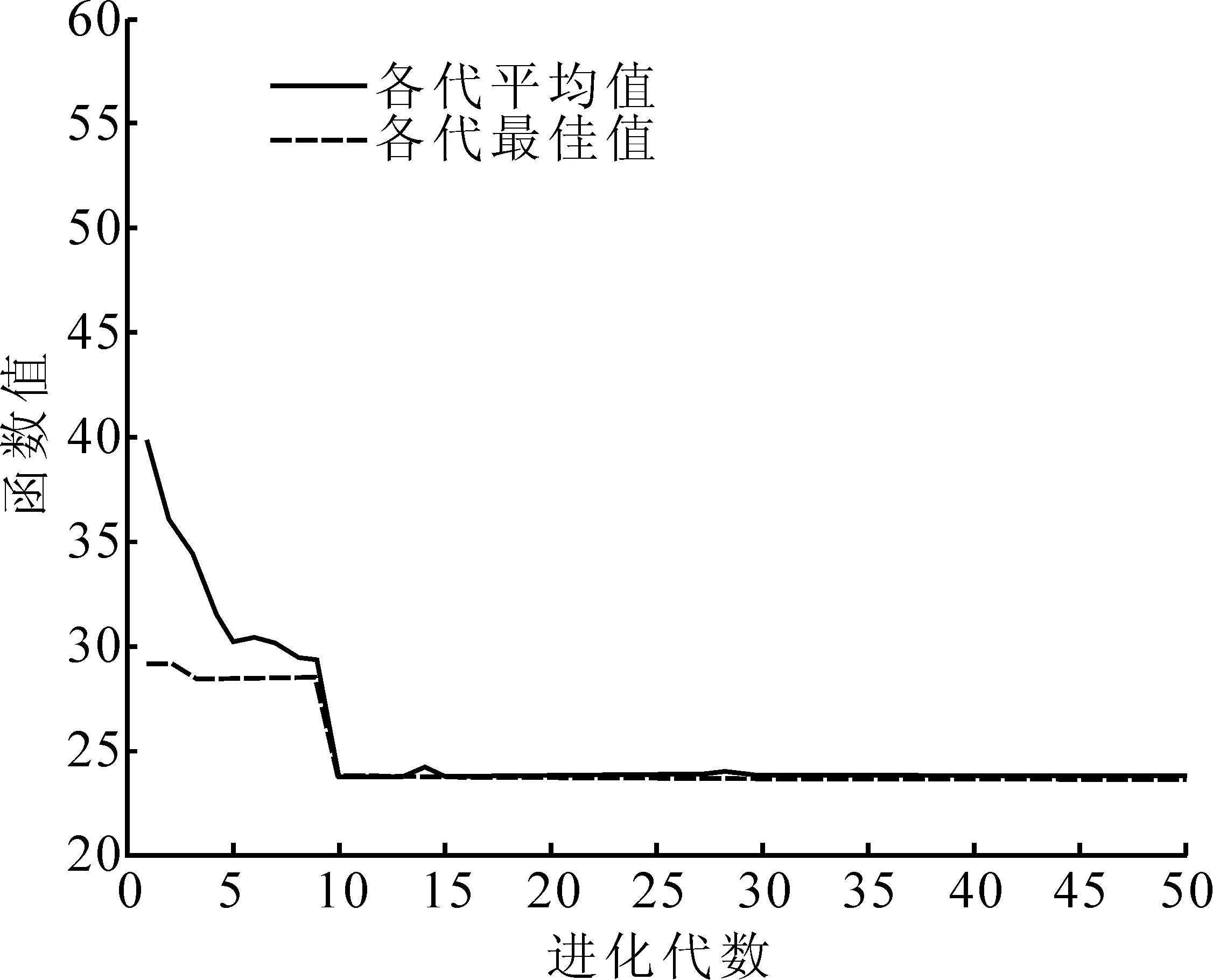
(a)表面粗糙度GA适应度函数值曲线

4 结语

本文研究了镍铬合金薄膜多工艺参数对单一薄膜性能的影响，并对镍铬合金薄膜的工艺参数进行了优化，主要得出以下结论。

(1)研究了镍铬合金薄膜的工艺参数对单一薄膜沉积性能的映射关系，分别建立了功率、压强、负偏压及基底温度与表面粗糙度和沉积速率的LSSVM预测模型。

(2)利用混合核函数作为LSSVM预测模型的核函数，并通过粒子群算法优化了混合核函数的参数，提高了预测模型的精度，最终得到LSSVM的非线性回归函数。

(3)通过遗传算法得到了薄膜沉积性能对应的工艺参数，表面粗糙度的最佳工艺参数为功率172W，压强0.8Pa，偏压129V，基底温度400℃；沉积速率的最佳工艺参数为功率200W，压强1.2Pa，偏压50V，基底温度100℃。

(4)建立了LSSVM和GA算法联合优化镍铬合金薄膜的优化模型，对今后开展试验研究和分析工艺参数与薄膜性能间的映射关系具有重要意义。