智能汽车换道轨迹的燃油经济性研究

金辉，赵延杰，光昊

（北京理工大学 机械与车辆学院，北京 100081）

智能汽车是一个集环境感知，运动规划和决策控制等多功能于一体的智能系统. 随着计算机、传感器及人工智能等技术的快速发展，智能汽车技术也有了长足的进步，这对提高智能汽车行驶安全性、驾驶舒适性及燃油经济性具有重大意义. 而在智能汽车技术发展的过程中，为了能让汽车进行安全快速经济地换道，汽车换道轨迹模型成为了国内外学者研究的热点.

目前理想的车辆换道轨迹模型主要有4 种：等速偏移换道轨迹模型、正弦函数换道轨迹模型、梯形加速度换道轨迹模型以及圆弧换道轨迹模型等.等速偏移换道轨迹模型在换道的初始与结束时刻，车辆的运动方向发生了突变，故该模型在实际的行驶中是无法实现的；圆弧换道轨迹模型在两段圆弧的两端点处曲率不连续，会发生跃变，因此该模型在实际行驶也是无法实现的；梯形加速度换道轨迹模型不够灵活，在调整换道过程会较为困难；而正弦函数换道轨迹模型在换道起点和终点处的路径曲率出现了最大值，不满足曲率要求. 基于这些理想换道轨迹模型，ZHOU 等[1]将3 次多项式函数作为换道轨迹，但其平滑性不好；李玮等[2]提出了正弦函数和双曲正切函数加权换道轨迹模型，其平滑性较好且曲率不会过大而其起点和终点曲率不为0；ZHANG 等[3]提出了等速偏移和正弦函数加权换道轨迹模型，该模型满足了曲率连续变化，起点和终点曲率为0，且曲率最大值较小.

根据石油输出组织的统计与预测，在2016-2040 年间的交通运输领域的能源消耗将占到全球总能耗的66.7%[4]；并依据国际能源署统计，总重量小于3 500 kg 的轻型汽车是全球化石燃料的主要消耗源，是污染物及温室气体的主要排放源. 随着节能意识和环保意识的日益加深，减少交通能耗，汽车节能减排刻不容缓，对智能汽车燃油经济性有了更高的要求[5]. 智能汽车变道作为车辆行驶中必不可少的驾驶行为之一，提高换道过程的经济性，优化汽车的换道轨迹，对燃油经济性，驾驶舒适性等方面具有重大意义.

文中基于智能汽车行驶的空间约束及运动轨迹曲率约束等，对换道轨迹模型进行设计，以实现车辆在换道过程中燃油经济性的最优.基于发动机瞬态油耗模型，确定平路行驶的最经济车速，并建立能满足各种约束的3 阶贝塞尔换道轨迹模型，且与现有的换道轨迹模型进行对比，通过Matlab/Simulink 与Carsim联合仿真验证，验证其经济性，最后对实验结果总结分析.

1 瞬态油耗模型

虽然国家在大力推广新能源汽车战略，但在2020 年全年汽车销量达到2 531.1 万辆的情况下，新能源汽车销量仅为136.7 万辆，占比为5.4%，故文中选择燃油车作为研究对象，对车道换道轨迹设计，使车辆进行经济换道，具有现实应用意义. 基于课题组的研究，采用GUANG 等[6]提出的BIT-TFCM3 燃油消耗模型. 为了兼顾油耗模型的准确性和运算速度，该模型是由2 部分瞬态油耗模型组成的. 当输入的车辆的速度v和加速度a满足式（1）时，则使用第1瞬态油耗模型，其预测精度较高；否则使用第2 瞬态油耗模型，其计算速度较快.

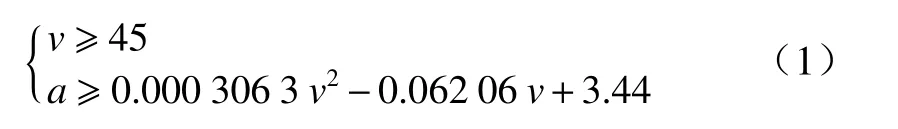
1.1 第1 瞬态油耗模型

第1 瞬态油耗模型[7]的稳态估计模块是以steadystate 循环匀速数据为基础建立Map 图，其输入为发动机的转速和转矩，通过二维插值得到稳态燃油消耗率m˙s；瞬态修正模块的输入为车辆的瞬时速度和加速度，该模块基于车辆比功率VSP(vehicle specific power, VSP)分区对油耗差值进行修正.

当VSP≥0 时，修正结构表达式为

当VSP＜0 时，采用2 个与速度有关的常数进行油耗率修正.

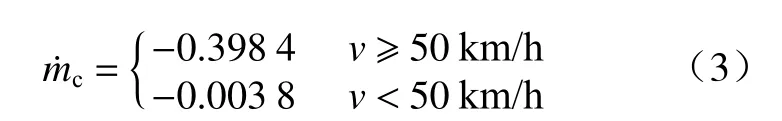
故可得修正后的油耗率为

1.2 第2 瞬态油耗模型

第2 瞬态油耗模型[8]的稳态估计模型也是采用steady-state 循环工况的测试数据为基础进行建模，通过多项式拟合的形式得到对数稳态燃油消耗率，如式（5）所示.

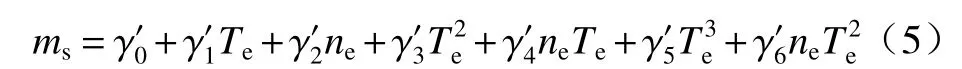
瞬态模块的建模数据来自UDDS 和US06，也利用多项式形式进行修正.

2 经济性评价条件

2.1 车辆行驶轨迹约束条件

目前大多数学者认为换道轨迹模型应该满足的2 个条件：车辆换道过程中的轨迹曲率应该是连续的，没有突变发生；在换道的开始与结束时刻路径曲率应为0，且易于转向操作.

根据车辆行驶的空间约束、车辆自身状态约束，并结合学者的观点，得到车辆在行驶时运动路径应该满足的3 个条件：①空间约束：在行驶过程中车辆的空间位置应该是连续变化的，不能出现位置瞬时突变现象，这就要求车辆的行驶轨迹是连续的；②车辆自身状态约束：在行驶过程中车辆的前轮转角应该是连续变化的，其角度值不应发生突变，这体现在运动轨迹函数中其导数应是连续变化的；③运动轨迹曲率约束：车辆行驶轨迹的曲率应该是连续变化的，没有突变现象. 由于直线行驶时轨迹的曲率为0，故当车辆发生换道行为前后均为直线行驶，这与学者所认同的第2 个条件约束相同.

2.2 直线行驶的最经济车速

SCHWARZKOPF 等指出，当车辆行驶于平直道路或者单一曲率道路上时，匀速行驶的燃油经济性最好. 因此，在进行换道轨迹经济性评价时，应把车辆在平路上直线行驶的经济性最佳车速作为换道行为前后的目标车速. 如图1 所示，当车速一定时，单位行驶燃油消耗量随挡位的升高而减少；当挡位一定时，燃油消耗量随车速的增加总体上呈现先降低再升高的趋势. 图中标出的坐标点表示车辆以6 挡行驶，以56 km/h 的车速每行驶1 m 的燃油消耗为0.051 7 mL，该点是曲线束的最低点. 故分析可知，采用瞬态油耗模型求出的直线行驶的经济车速及最优单位行驶距离燃油消耗量为

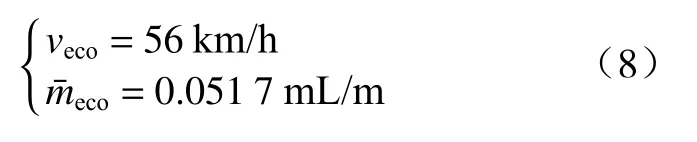
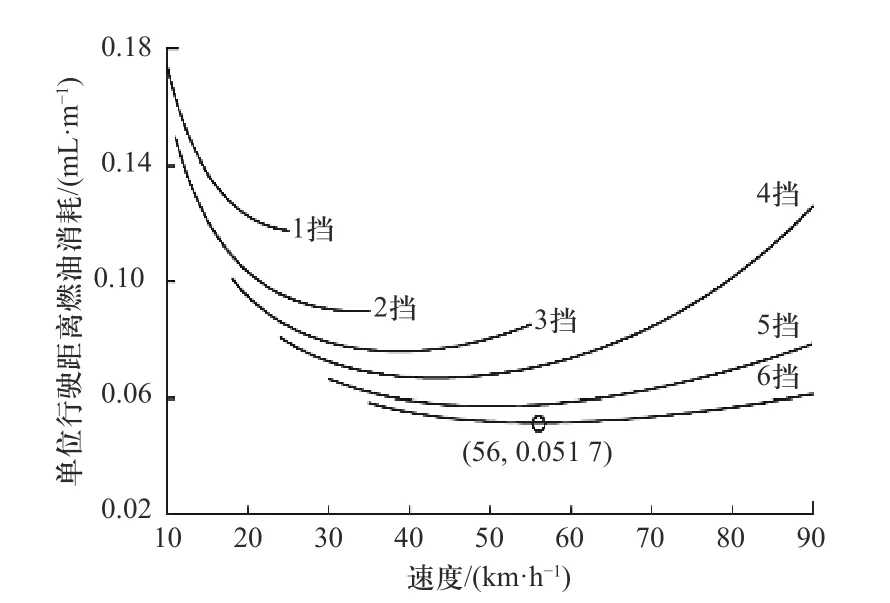
图1 单位行驶距离燃油消耗Fig. 1 Fuel consumption in unit distance

在车辆换道过程中运动方向变化不大，但仍存在着轨迹弯曲度不为0 的变化过程. 有研究表明，在行驶轨迹弯曲度不同的情况下，车辆的稳态最优经济车速以及对应的单位距离燃油消耗是不同的，利用瞬态油耗模型绘制了相应的变化曲线，如图2 所示. 由图2 可知，当轨迹弯曲度为0 时，两条曲线与左右两纵轴的交点值对应为56 km/h 和0.051 7 mL/m.当轨迹弯曲度开始增加时，最优经济车速曲线的下降十分缓慢，近似于水平线，故在换道的过程中，我们把直线行驶的最经济车速作为车速. 而单位距离燃油消耗出现了小幅度的增加，这是由于车轮开始受到侧偏力的作用；随着轨迹弯曲度不断增加，最优经济车速曲线开始明显下降，单位距离油耗开始明显增加. 故轨迹曲率对换道经济性有着明显的影响.

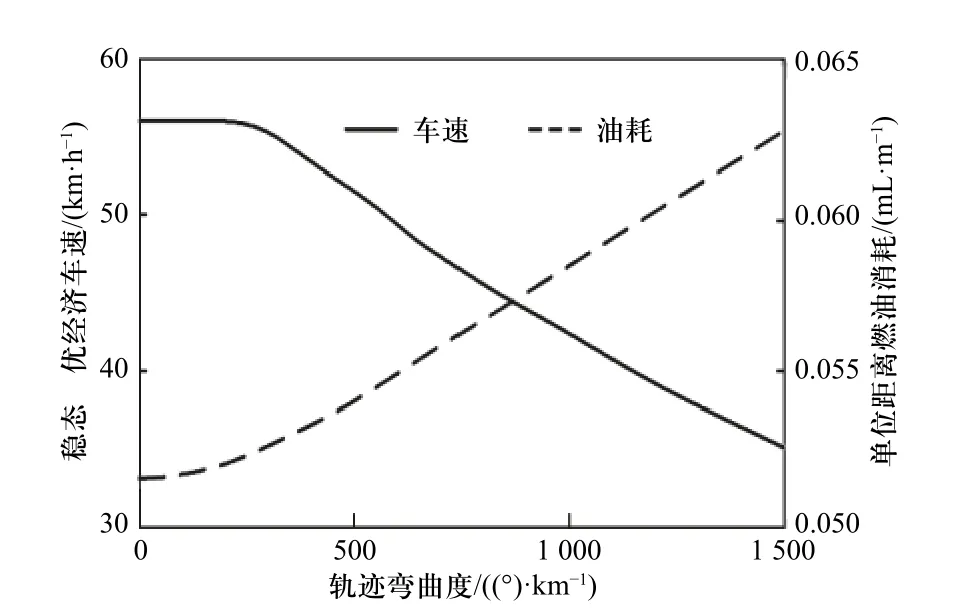
图2 经济车速及单位距离油耗变化曲线Fig. 2 Curve of economic speed and fuel consumption in unit distance

3 换道轨迹模型

3.1 对比换道轨迹

由于多项式函数的可调节性较好，可通过增减项次以及调整系数来调节轨迹的平滑性，文中选择在国外知名期刊发表的论文中的3 次多项式换道轨迹（下文统一简称polynomial）作为一个对比组，其表达式为

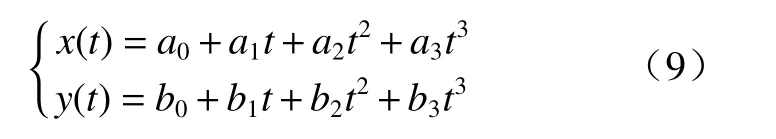
式中：x(t)为纵向位移；y(t)为横向位移；t为换道时间.

通过边界及求导条件可知

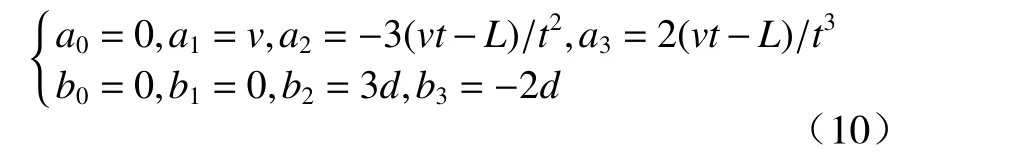
式中：v为车速，m/s ；t为换道总时间，s;L为换道纵向长度，m;d为换道横向长度，m.

正弦函数和双曲正切函数加权换道轨迹（下文统一简称sin-tanh）以及等速偏移和正弦函数加权换道轨迹（下文统一简称x-sin），是两种计算相对简单的平滑过渡曲线，而且它们的曲率都是连续变化的，符合车辆的实际行驶条件，并结合前言部分对换道轨迹优缺点的分析，发现sin-tanh 和x-sin 两种换道轨迹模型性能较优且被广泛使用，因此文中把sin-tanh和x-sin 两种换道轨迹作为对比组，最终来进行实验结果分析，其表达式分别为

3.2 3 阶贝塞尔换道轨迹

贝塞尔曲线在起始与终点的曲率为零，是被包含于所有控制点组成的凸包内，该曲线整体连续平滑，为了满足汽车行驶的约束条件，采用3 阶贝塞尔曲线（下面统一简称Bezier）. 在车辆换道过程不考虑碰撞的危险，故把整个换道路径分为2 个对称部分，文中对第1 部分路径研究贝塞尔曲线，从而得到整体换道轨迹曲线. 这里假设车道宽度即为两车道中心线的间距d，完成换道的过程中车辆沿车道线行驶的位移为L，车辆运行时的初始方向为坐标轴的正方向，车辆向左侧变道，Bezier 换道轨迹示意图如图3所示.

图中共有4 个点，其坐标A0(X0，Y0),A1(X1,Y1),A2(X2,Y2)，A3(X3,Y3).其余在图3 已进行了说明. 基于贝塞尔曲线的换道轨迹重点在于控制点的选取，控制点对轨迹的位置和形状有着决定性的影响. 文中根据车辆的起始点和行驶约束条件确定控制点的坐标. 换道轨迹的参数方程为

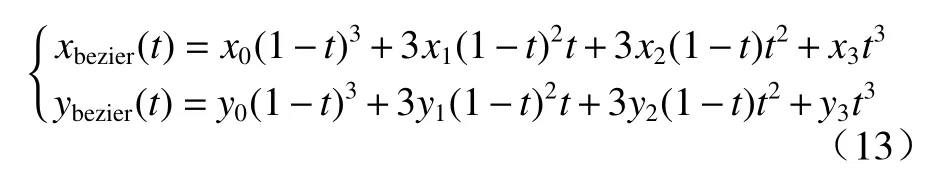
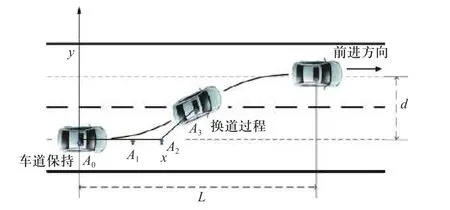
图3 贝塞尔换道轨迹示意图Fig. 3 Schematic diagram of Bezier lane changing trajectory

通过边界条件及求导条件可得A0、A1、A2、A3，控制点确定后，其换道轨迹曲线如图4 所示.

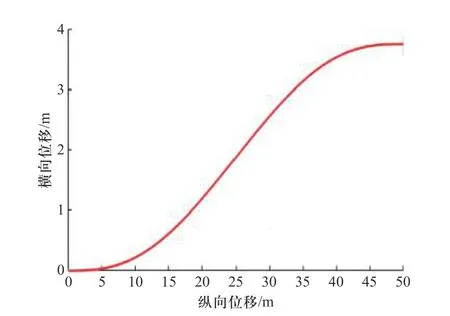
图4 贝塞尔换道轨迹示意图Fig. 4 Curve of Bezier lane changing trajectory

4 实验结果分析

4.1 联合仿真模型

在换道轨迹经济性评价中将用到联合仿真，选择Carsim 软件中某轿车作为仿真车辆，搭建的联合仿真整体模型如图5 所示，主要是由速度控制模块和瞬态油耗模块组成. 在Carsim 中输入要用到的换道轨迹模型，车辆按照预期道路轨迹行驶. 文中采用定速巡航算法（cruise control, CC），车辆以直道上的经济车速行驶，并在Simulink 中设计速度控制模块，通过对车辆的油门信号和制动信号进行控制，进而达到对车速控制的目的. 设置Carsim 的外部接口，将Carsim 中设置的车型配置信息、换道仿真场景发送到Simulink 仿真模型中，作为瞬态油耗模块的输入量，来计算其燃油消耗，评价经济性.

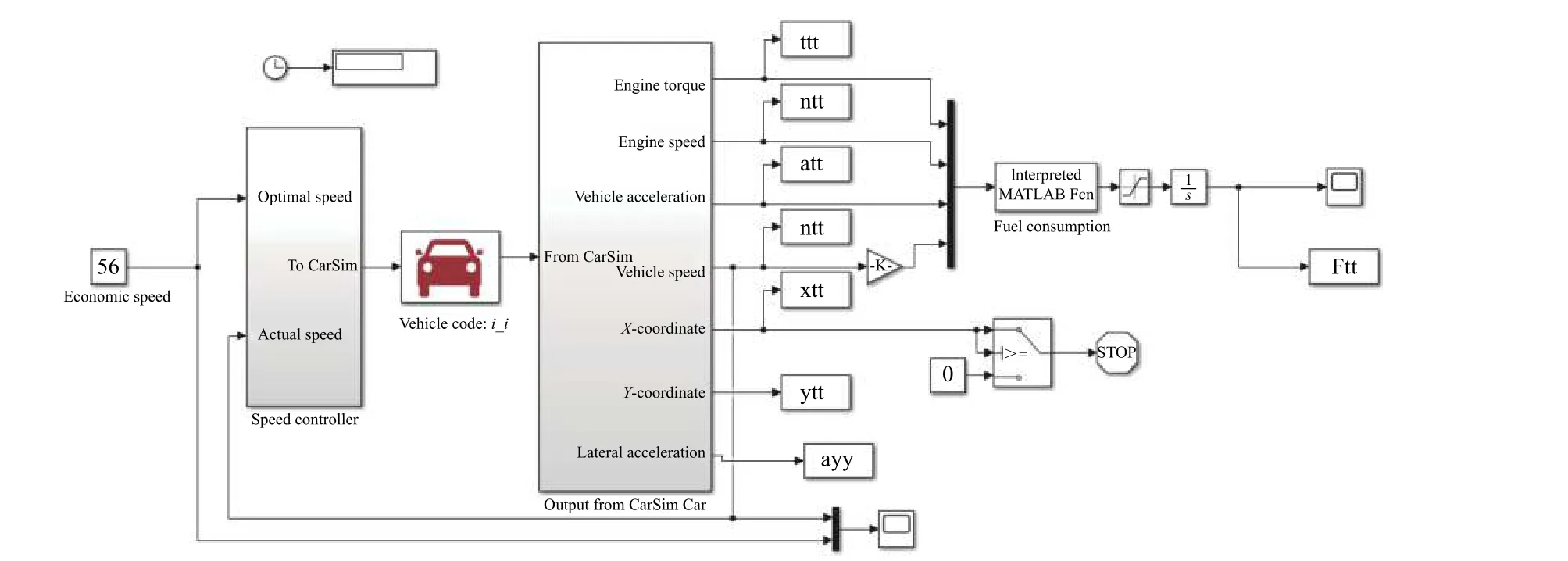
图5 联合仿真整体模型示意图Fig. 5 Schematic diagram of co-simulation overall model

4.2 仿真结果分析

车辆以56 km/h 的经济车速行驶，换道纵向距离分别为50 m 的条件下对Polynomial 及Bezier 两种换道轨迹进行仿真结果数据如表1 所示，其曲率变化比较如图6 所示.

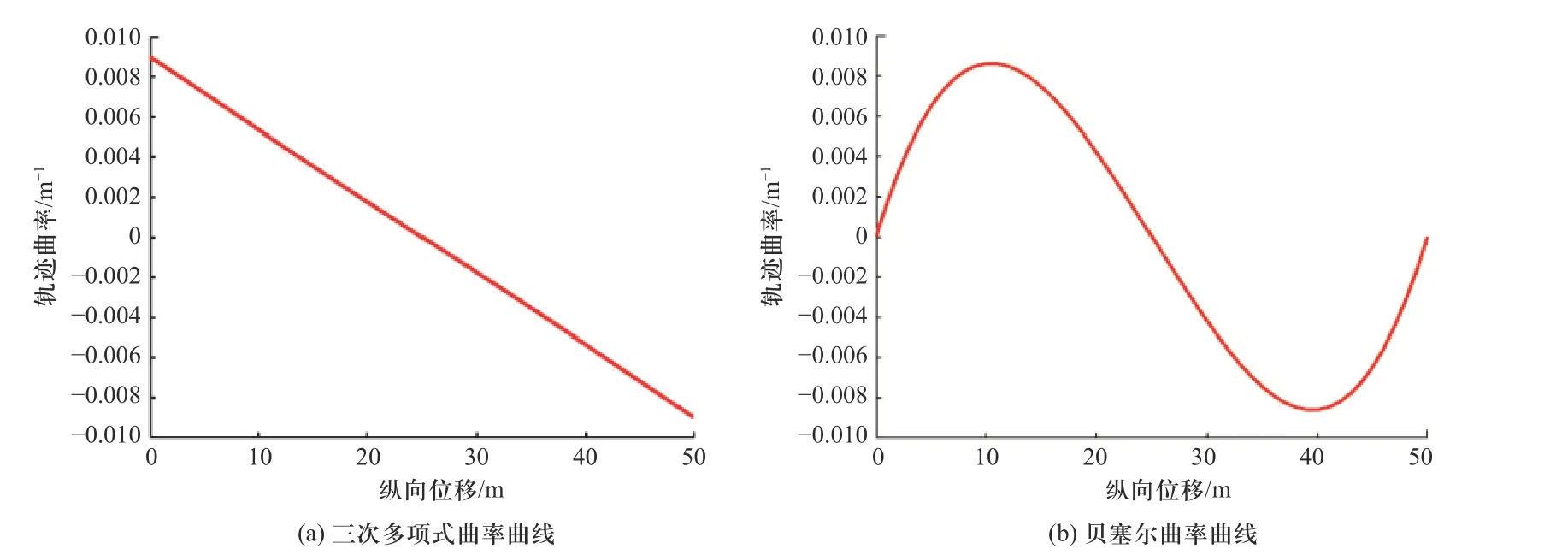
图6 曲率变化示意图Fig. 6 Schematic diagram of curvature change

表1 换道轨迹经济性比较Tab. 1 Economic comparison of lane changing trajectory

根据表1 可知，3 次多项式比贝塞尔换道轨迹的燃油消耗与最大横向加速度值稍小些，但从图6 来看，3 次多项式换道轨迹在起点和终点的曲率值较大，这极大地降低了行驶安全性，Bezier 换道轨迹模型的曲率变化连续且轨迹初末位置的曲率为0，同时保证了换道开始与结束时刻的车辆前轮转角为0，与车辆实际运行状况相符. 故虽然3 次多项式的经济性更好些，但综合安全性考虑，文中的贝塞尔换道轨迹能更好地应用于实际换道中.

车辆以56 km/h 的经济车速行驶，换道纵向距离为50 m 的条件下对sin-tanh、x-sin 及Bezier 3 种换道轨迹进行仿真结果数据如表2 所示.

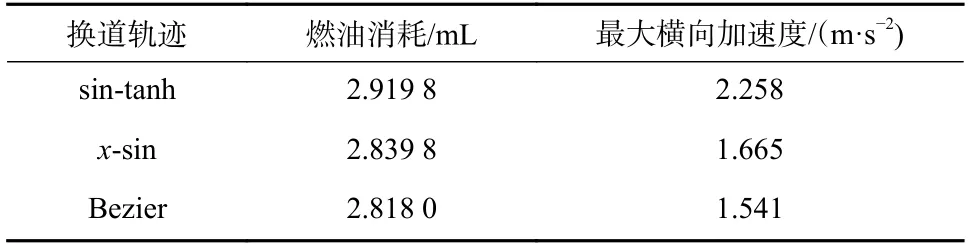
表2 换道轨迹经济性比较Tab. 2 Economic comparison of lane changing trajectory

由表2 可知，Bezier 比sin-tanh 和x-sin 换道轨迹分别节油约3.49%和0.77%，Bezier 换道燃油消耗最低； bezier 的最大横向加速度值比sin-tanh 和x-sin 分别降低了约31.75%及7.45%，车辆的横向加速度均小于2.5 m/s2，在合理的横向加速度区间内，这保证了轮胎工作在线性区间内，且根据三者数值的比较，Bezier 换道轨迹是最优的.

为了证明在不同的换道纵向距离下，Bezier 换道轨迹模型仍是最优的，文中给出了在换道的目标车速为56 km/h 时，仿真出3 种换道轨迹下的换道单位距离燃油消耗随换道纵向距离变化曲线图如，如图7(a)所示. 由图可知，当换道纵向位移较小时，3 种换道轨迹模型的单位燃油消耗都随着位移的增加而急剧减少，当距离达到90 米时，减少的趋势开始明显变慢了，在换道纵向位移小于120 米时，3 种换道方法的燃油消耗还是有着明显的差距的，sin-tanh 换道轨迹的油耗最高，x-sin 的换道轨迹的油耗稍高于Bezier 换道轨迹；但在位移大于120 后，三者的油耗变化曲线逐渐接近并趋于重合，且当换道纵向位移足够长时，将无限接近前面所求的直线行驶经济车速所对应的单位行驶距离燃油消耗量.

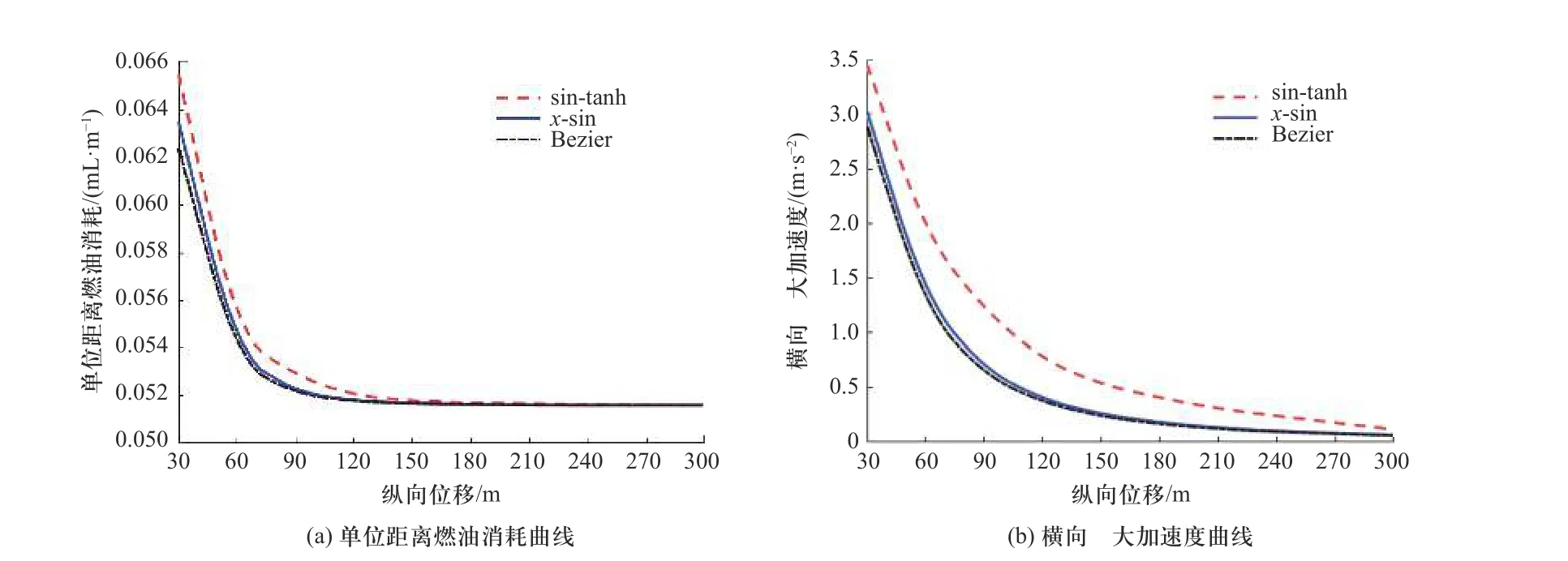
图7 换道轨迹经济性综合分析Fig. 7 Economic comprehensive analysis of lane changing trajectory

图7(b)给出了换道过程的目标车速为56 km/h时，在不同换道纵向位移下采用以上3 种轨迹进行车道变换时的最大横向加速度变化曲线图.由图可知，当换道纵向长度小于40 米，sin-tanh 和x-sin 换道轨迹的横向加速度最大值超过了2.5 m/s2，而对于贝塞尔换道轨迹来说，这个值是37 米，因此，贝塞尔轨迹能在更短的纵向位移内实现车道的变换，也就是说，贝塞尔换道轨迹可以允许的换道纵向位移的范围是最大的. 当换道纵向位移较小时，3 种换道轨迹的最大横向加速度都随着换道纵向位移的增加而急剧减小，直到120 米左右减小趋势开始明显变缓慢；另外，随着车辆换道纵向位移的增加，3 个最大横向加速度变化曲线都在逐渐变小并相互接近，而在150 米以后，x-sin 换道轨迹和贝塞尔换道轨迹开始趋于重合，而sin-tanh 换道轨迹的最大横向加速度仍然稍高一点.

通过图7 可知，3 种换道轨迹的燃油消耗和加速度变化曲线是对应相似的，而且通过3 条换道轨迹的比较可知，贝塞尔换道轨迹的油耗是最少的，最大横向加速度值也是最小的，在保证燃油经济性的同时，这有利于减少轮胎的磨损，提高车辆的乘坐舒适性，充分地证明了贝塞尔换道轨迹模型的优越性.

5 结 论

文中提出了一种基于瞬态油耗模型进行换道轨迹经济性评价的方法. 利用发动机瞬态油耗模型求出了车辆直线行驶的经济车速及对应的最优单位行驶距离的燃油消耗，在保证换道安全、舒适及满足换道轨迹约束的条件下，设计了换道轨迹模型.通过Matlab/Simulink 和Carsim 联合仿真，对不同类型的换道轨迹模型进行了燃油经济性评价，得到不同换道轨迹对应的油耗及横向加速度. 通过仿真结果可知，文中设计的曲率更小，轨迹更平滑的贝塞尔换道轨迹的油耗分别比已有的sin-tanh 和x-sin 换道轨迹节油3.49%和0.77%，其最大横向加速度值也分别比sin-tanh 和x-sin 换道轨迹降低了31.75%及7.45%. 因此在保证智能汽车安全舒适行驶的前提下，贝塞尔换道轨迹的油耗是最少的，最大横向加速度值也是最小的，这充分证明了贝塞尔换道轨迹模型的优越性.