变构型陆空平台动态起降轨迹规划研究

魏巍，范康迪，王若琳，赵默雷，赵之然，王剑峰

（1. 北京理工大学 车辆传动国家重点实验室, 北京 100081；2. 北京理工大学 重庆创新中心, 重庆 401120；3. 北京千方创新科技有限公司, 北京 102299）

陆空平台具有行驶时续航时间长的优点，也具备飞行时的高通过性. 许多国内外学者设计了不同构型的陆空平台，有飞行与行驶机构独立驱动且不可变形的陆空平台，如南安普顿大学的SuperB[1]和清华大学的“猛狮”[2]；有飞行机构提供行驶动力的陆空平台，如伊利诺伊理工大学的HyTAQ[3]；有飞行机构可偏转的陆空平台，如北京理工大学设计的变构型陆空平台[4-5]和瑞典的Linnaeus 概念平台[6]. 陆空平台的多域机动能力使其能在隧道巡检、灾区搜救等复杂场景应用，陆空平台静态起降时存在多次减速停止的情况，而动态起降具有连续机动能力，为满足陆空平台机动性能方面的要求，需要对动态切换的轨迹基于时间进行优化.

国内外许多学者对移动机器人轨迹规划进行了研究. 牛国臣等[7]采用两次改进的5 次多项式进行规划，避免与物体的碰撞. 王莹等[8]针对可动边界问题，通过选定一系列终点候选位置，利用三次多项式拟合路径，最终根据目标函数选取最优轨迹. 唐刚等[9]在目标函数中添加走廊约束，并建立偏离评估函数，基于最小snap 方法生成接近直线的轨迹. 张洲宇等[10]定义时间、航程和燃料的多目标函数，基于二次贝塞尔曲线规划无人机轨迹.

目前陆空平台对飞行与行驶状态研究较多，针对陆空模式的转换研究较少. 为探究陆空模式转换的机动性问题，规划静态切换与动态切换两种陆空切换模式的轨迹，对比两者时间证明动态切换的高机动性，设计飞行控制器验证动态切换轨迹的可控性.

1 飞行动力学模型

变构型陆空平台如图1 所示，飞行模式下，4 个空用电机驱动旋翼提供升力，涵道提供附加升力.行驶模式下，4 个陆用电机驱动涵道提供行驶动力. 陆空切换模式下，2 个舵机带动涵道旋翼进行偏转. 此构型冗余质量较小，飞行升力高，旋翼安全性好.

图1 变构型陆空平台示意图Fig. 1 Schematic of deformable aerial-ground platform

1.1 坐标系建立

地面坐标系即惯性坐标系为Oxyz，机体坐标系为Obxbybzb，如图2 所示.

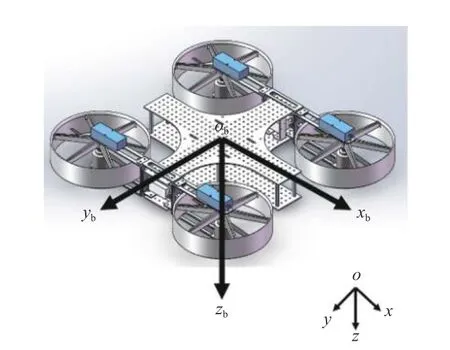
图2 坐标系Fig. 2 Coordinate system

1.2 受力分析

对模型做出如下假设：

①陆空平台为刚体.②质量为常数，重心位置不变.

③陆空平台只受重力和旋翼拉力.

④地面为惯性参考系.

基于牛顿-欧拉方程，有：

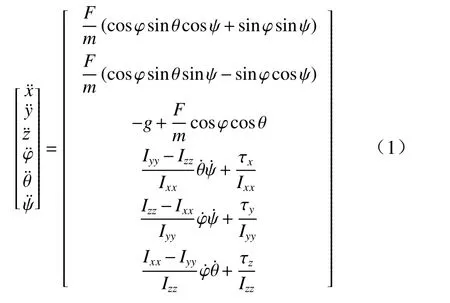
式中：F为在机体坐标系zb轴的旋翼总拉力；m为陆空平台质量；g为重力加速度； φ为滚转角； θ为俯仰角；ψ为偏航角； τx、 τy、 τz分别为xb、yb、zb轴力矩；Ixx、Iyy、Izz分别为陆空平台沿xb、yb、zb轴的转动惯量；转动惯量与偏转角的关系如图3 所示.

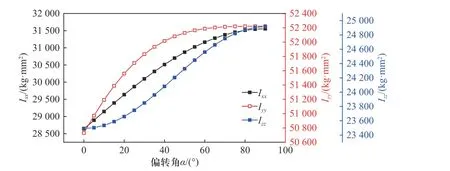
图3 随偏转角变化的转动惯量曲线Fig. 3 Moment of inertia curve varying with deflection angle

陆空平台所受拉力F、力矩 τx、 τy、 τz与4 个飞行电机转速 ω1、 ω2、 ω3、 ω4的关系为

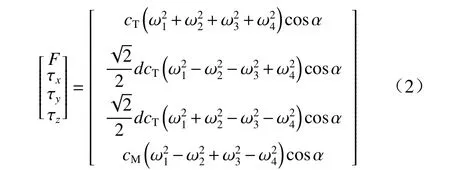
式中：cT为旋翼的升力系数；cM为旋翼的转矩系数；α为涵道偏转角；d为旋翼质心到机体质心的距离.

2 动态切换轨迹规划

陆空平台的动态切换为Obxbzb内的二维平面运动，y方向位移与偏航角 ψ不变，因此规划目标为平面位置x、z和偏转角 α.

研究由陆到空的模式切换如图4 所示.

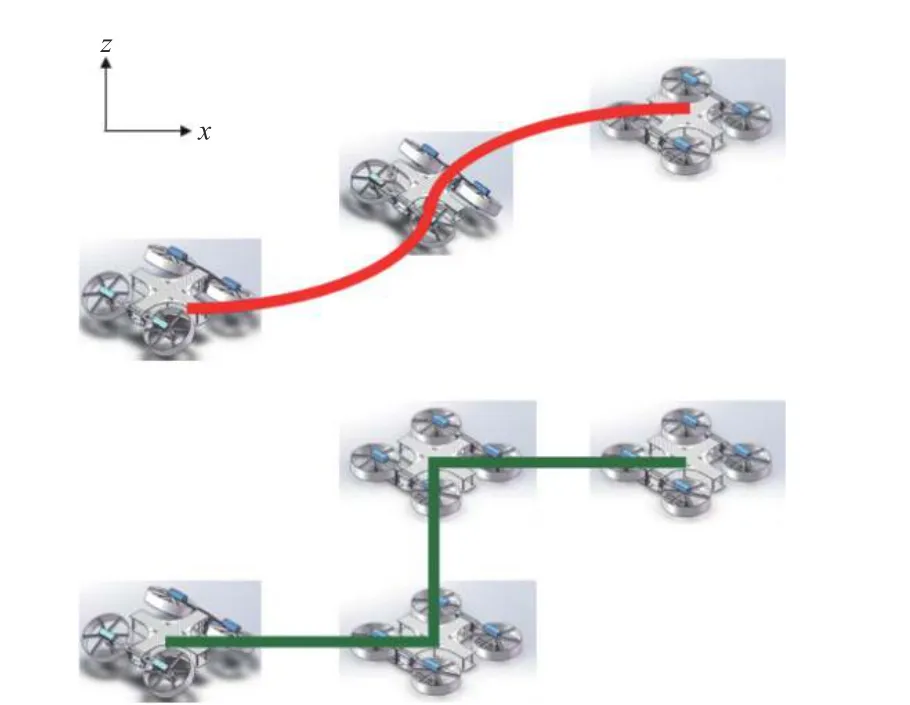
图4 陆空动态切换与静态切换示意图Fig. 4 Schematic diagram of dynamic and static switching between land and air

2.1 目标函数

当目标飞行高度h已知，陆空切换终点在水平直线上变动，对于右端可动边界点，通过将可动边界在(0,xmax)内离散化，获得终点的数据点集，对所有边界点进行轨迹拟合，采用目标函数筛选最优轨迹. 轨迹规划的目标函数J为动态切换相对静态切换所减少时间占静态切换时间的比例.

式中：tj为静态切换时间；td为动态切换时间.

2.2 动态切换

假设动态切换轨迹规划在x方向以速度vx匀速运动，起飞时偏转角为α(t=0)，飞行的目标高度为h，则边界条件如下：

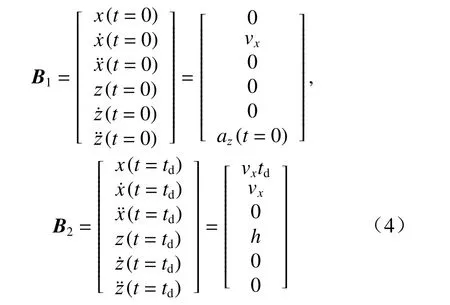
当偏转角变化时，陆空平台的最大升力随之改变，因此，动力学约束与偏转角存在耦合关系. 将轨迹分为两段，偏转角在前1/p时间内完成涵道偏转角从α(t=0)到0°的变化过程，后一段时间偏转角保持0°不变，从而实现偏转角 α和平面位置x、z的分层规划.

设涵道偏转角随时间变化的函数为一次函数，则

偏转角0°时高度方向最大加速度为azmax,则动力学约束为

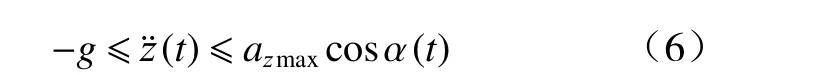
基于5 次多项式，分别在x和z方向表示动态切换轨迹函数.

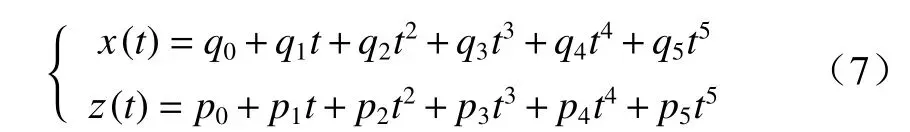
由此可得

2.3 静态切换

静态切换边界点与动态切换一致，其轨迹分为3 段：行驶减速段、飞行上升段和前飞段. 行驶减速段以最小行驶加速度a′xmin从vx减速到0，假设减速段时间为tj1，然后以tj2的时间使涵道偏转至水平. 飞行上升段若高度h较低，则前半段以z方向最大加速度飞行，后半段以z方向最小加速度减速飞行至高度h悬停，假设上升段时间为tj3. 前飞段前半段以x方向最大加速度飞行，当加速到vx时匀速前进，假设前飞段时间为tj4. 综上，静态切换时间tj=tj1+tj2+tj3+tj4.

2.4 轨迹规划流程

在陆空转换的过程中，陆空平台的终点(x,h)为可动边界，规划过程中以J为目标函数，针对x、h进行优化，轨迹规划的流程如图5 所示.

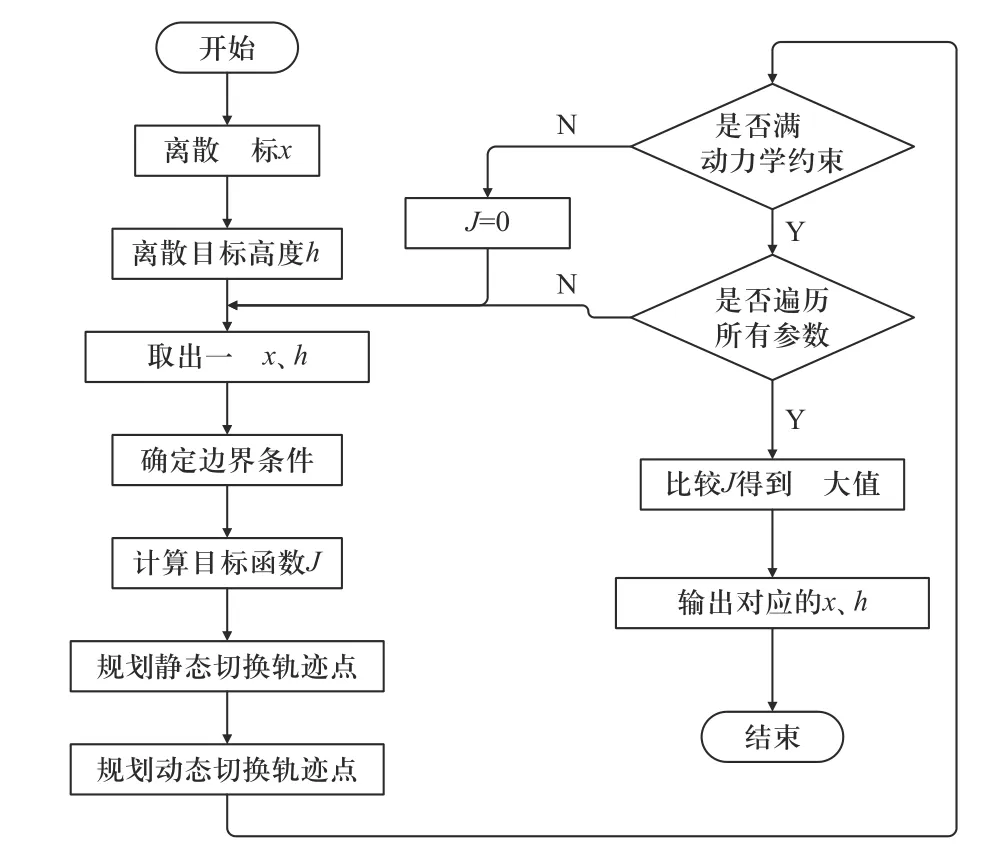
图5 轨迹规划流程图Fig. 5 Trajectory planning flowchart

3 仿 真

基于Matlab 规划动态切换轨迹，基于Simulink搭建陆空平台的控制器与模型，以动态切换轨迹作为控制器输入，进行轨迹跟踪控制仿真. 给出关键参数如表1 所示.

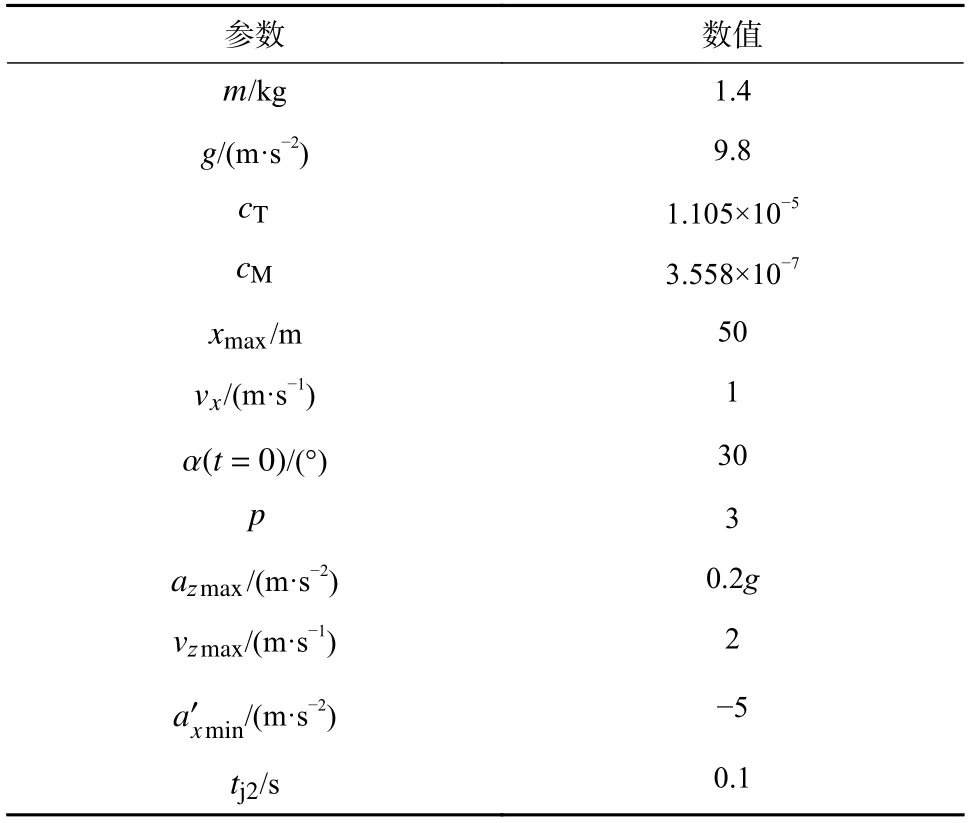
表1 关键参数Tab. 1 Key parameters

3.1 动态切换轨迹规划仿真

轨迹规划仿真结果如表2 所示.

表2 仿真结果Tab. 2 Simulation results

如图6 所示，可以看到目标函数J随轨迹终点坐标x和h的变化趋势，J=0的直线段表示不符合动力学约束，忽略该直线段，那么J随x增长呈现出下降的趋势. 当x=6 m 不变时，J随h的增长而增长. 但当h增加时，J随x变化曲线中J的最大值随之减小，即max(J(x))随h增加而减小，因此，当轨迹规划追求J的最大值时，将规划得到h=0.1 m（h离散时的最小值）时的轨迹，在实际陆空转换中h并不是越小越好，考虑室内应用场景，选择h=1.5 m作为输入参数进行轨迹规划.

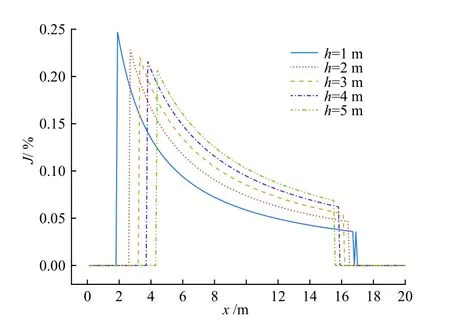
图6 J 随x、h 变化的关系图Fig. 6 The relationship diagram of J with x and h

如表3 所示，相比静态切换，动态切换时间缩短了23.02%，仿真表明动态切换相比静态切换具有更好的机动性.

表3 h=1.5 m 时的仿真结果Tab. 3 Simulation results when h=1.5 m

如图7 和图8 所示，动态切换轨迹平滑，加速度连续变化，加速度曲线符合动力学约束和边界条件.

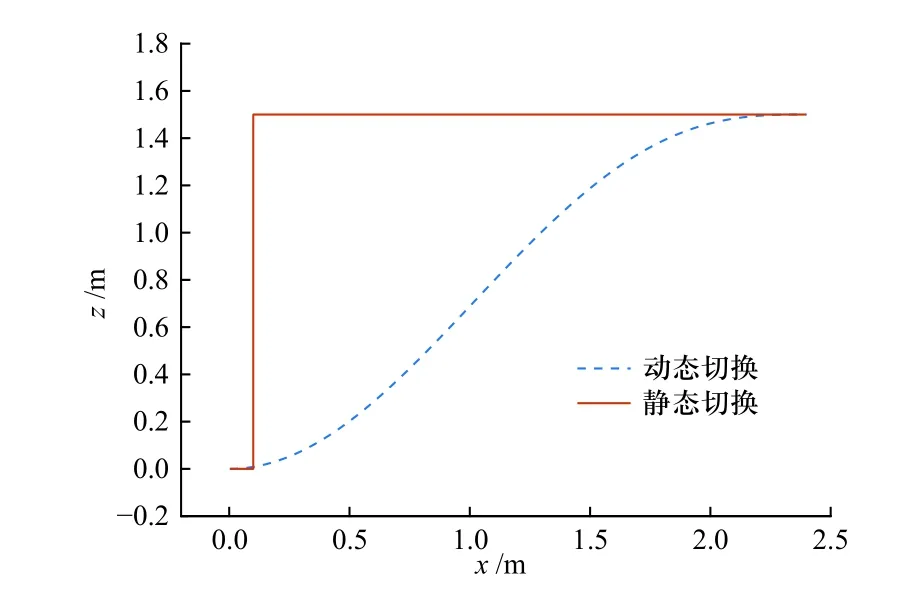
图7 飞行路径Fig. 7 Flight path

图8 动态切换时z 向加速度曲线Fig. 8 z-direction acceleration curve during dynamic switching

3.2 动态切换轨迹跟踪控制仿真

基于PID 算法[11]设计陆空平台的飞行控制器，对动态切换轨迹跟踪控制，控制框图如图9 所示.

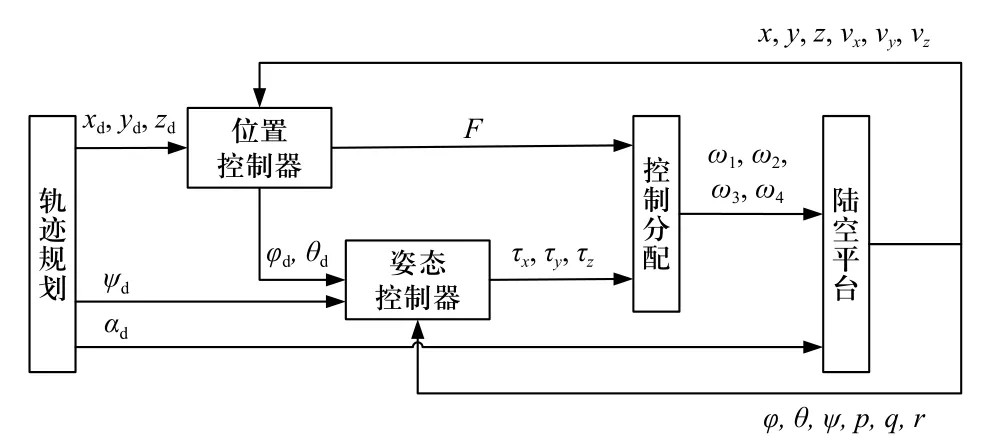
图9 轨迹跟踪控制框图Fig. 9 Trajectory tracking control block diagram

位置与姿态控制器采用双闭环结构，外环为P控制器，内环为PID 控制器. 首先调试姿态控制器，然后调试位置控制器，直到具有较好的控制效果，各通道控制器参数如表4 所示.

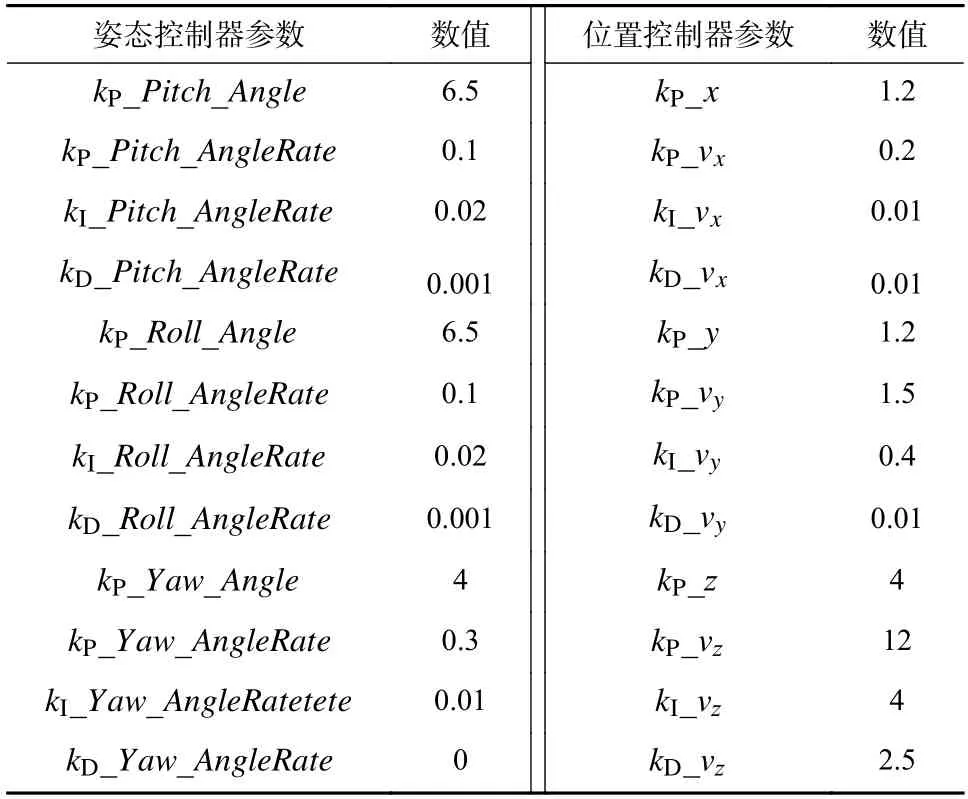
表4 控制器参数Tab. 4 Controller parameters

如图10 所示，实际飞行轨迹较为平滑，与期望轨迹误差较小，且在终点处基本无超调，控制器的跟踪控制效果较好.

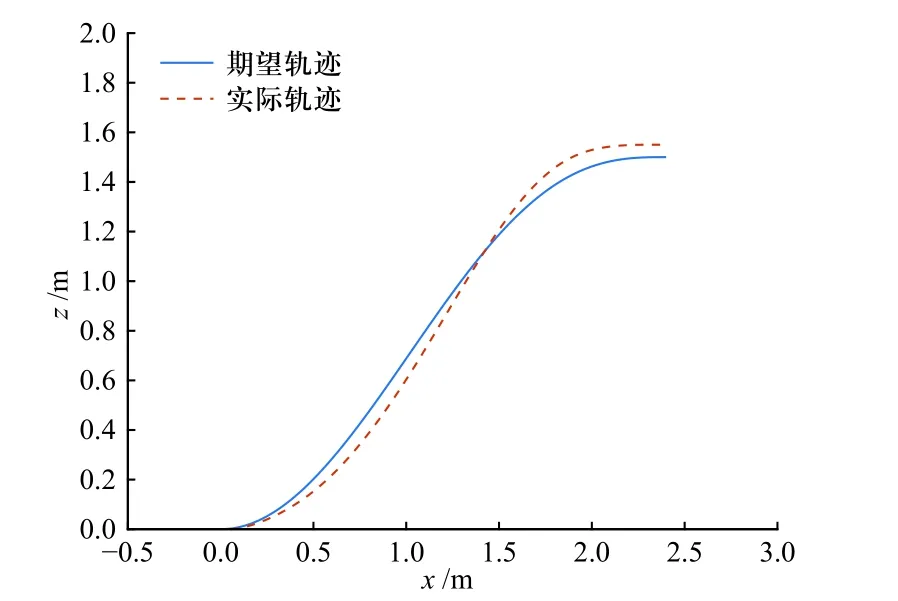
图10 PID 轨迹跟踪控制Fig. 10 PID trajectory tracking control

4 结 论

通过对陆空平台陆空模式静态切换和动态切换进行轨迹规划，并设计PID 控制器对动态切换轨迹跟踪控制，结论如下：

采用5 次多项式规划动态切换轨迹，规定静态切换运动方式，仿真表明当h不 变时，目标函数J随x增加而减小；当x不变时，目标函数J随h增加而增加；J随x变化曲线中J的最大值随h增加而减小；当高度h=1.5 m时动态切换时间相比静态切换时间缩短了23.02%.

通过PID 控制方法设计陆空平台飞行控制器，仿真表明能较好地跟踪动态切换轨迹.