基于势场法的无人车局部动态避障路径规划算法

翟丽，张雪莹，张闲，王承平

（1. 北京理工大学 机械与车辆学院, 北京 100081；2. 电动车辆国家工程研究中心, 北京 100081）

路径规划作为无人车领域关键技术之一，是无人车运动控制的前提，路径规划的好坏决定了无人车辆能否平稳安全的行驶，也是环境信息感知系统和车辆智能控制的桥梁[1]. 局部路径规划能够实时获取障碍物信息并进行实时规划，使无人车有更好的环境适应性，因此成为当前国内外研究重点. 目前常见的局部路径规划算法有遗传算法、模糊逻辑算法、神经网络算法、人工势场法等. 与其他路径规划算法相比，人工势场法定义直观，模型结构简单，不需要很大的计算量就可以实时避障并完成规划任务，在实时避障与平滑轨迹控制等方面得到了广泛应用[2-4].但同时存在复杂环境中目标不可达以及局部最优等问题[5].

近几年，研究人员针对传统人工势场法存在的缺陷提出了各种改进措施，主要包括增设道路或者速度势场、改变斥力势场与斥力调节因子、增设虚拟目标点等措施. 陈相茹[6]基于传统势场法提出了车道速度吸引势和跟车吸引，完善了车辆行驶路径模型，但是当道路模型改变时，该方法的适用性则有待进一步研究. 赵明等[7]提出自适应域-人工势场法，通过动态调节势场值来解决局部极小值问题，但是当障碍物影响范围较大时，这种方法会极大增加机器人的运动路径. 韩宇洪[8]在斥力函数中引入车辆与目标点之间的距离，通过调节斥力解决局部最小值问题，但该方法不能对侧向移动障碍物进行有效避障. 陈冠星等[9]通过增添虚拟目标点引导机器人走出陷阱区域，但是未解决目标不可达问题. 张涌等[10]通过改进斥力调节因子和斥力作用域来进行同向超车避障规划，但是该算法未解决侧向移动障碍物工况下的避障路径规划.

文中基于传统人工势场法，建立了包含障碍物和目标点的行车风险场，设置动态避障窗口，在每个避障窗口内对避障路径不断进行规划. 通过改进势场力来解决复杂环境下目标不可达和局部最优的问题. 考虑车辆运动学与动力学约束，对复杂动态障碍物工况进行分析并生成融合算法，最终生成一条能够有效躲避障碍物且顺利到达目标点的最优路径.

1 行车风险场的构建

1.1 目标点引力势场

由目标点产生的引力势场与车辆到目标点的距离相关，设车辆在二维坐标系中的位置坐标为x，目标点的坐标为xgoal,则引力势场函数Uatt的表达式为

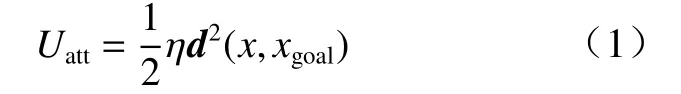
式中: η为引力势场正比例系数;d(x,xgoal)为车辆当前位置与目标点之间的距离一个矢量，方向从车辆指向目标点. 对引力势场函数求导可得到引力函数Fatt，其表达式为

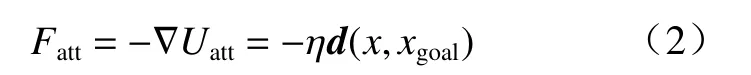
1.2 障碍物斥力势场

与引力势场相似，由障碍物产生的斥力势场与车辆到障碍物的距离相关，车辆与障碍物的距离越短，其斥力势能的值就越大. 车辆与障碍物之间的距离超过障碍物影响范围d0时，斥力势能为0. 根据斥力势场的特点，斥力势场函数Urep的表达式可表示为

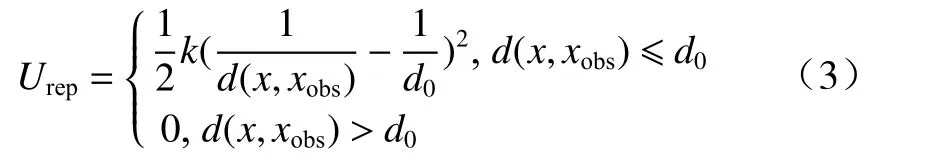
式中：k为斥力势场正比例系数；d0为障碍物影响范围；x为车辆的位置坐标；xobs为障碍物的位置坐标；d(x,xobs)为车辆与障碍物之间的距离.

对斥力势场函数求导可得到斥力函数Frep，Frep的方向就是斥力势能下降最快的方向，即引力势场的负梯度，其表达式为

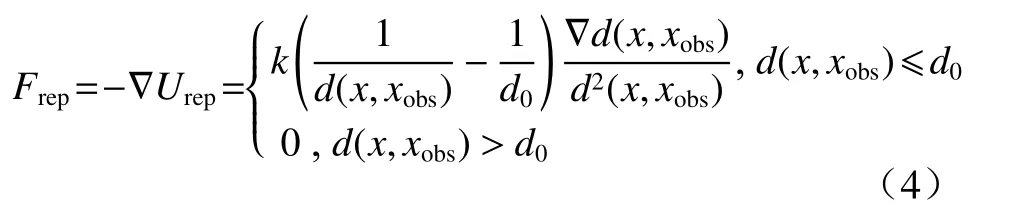
由式(4)可知，当车辆与障碍物的距离小于d0时，斥力值的大小与车辆和障碍物的距离成反比，当无人车与障碍物之间的距离趋近于0 时，斥力势场对无人车的斥力趋近于无穷大.

1.3 行车风险场

车辆在目标点和多个障碍物构成的合势场作用下运动，设对车辆产生斥力影响的障碍物个数为n,通过势场叠加，可得到合势场函数U，其表达式为

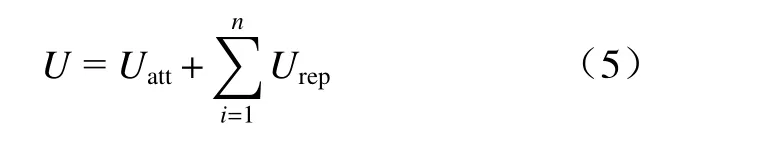
车辆受到的合力F分别由引力函数Fatt和斥力函数Frep矢量叠加得到，其表达式为

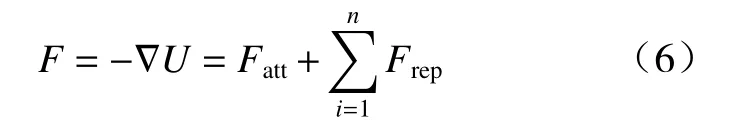
2 传统势场法缺陷改进

2.1 局部极小值问题改进

局部最小值是指在路径规划过中，目标点对车辆的引力与障碍物对车辆的斥力大小相等，方向相反，即车辆受力平衡，无法继续向目标点移动. 本节对传统人工势场法存在的局部极小值问题进行分析，并提出解决方法，然后通过仿真分析验证所提出方法的有效性.

2.1.1 障碍物位于车辆和目标点之间

如图1(a)所示，障碍物位于车辆与目标点之间，车辆陷入局部极小值. 为了打破车辆局部极小值的境况，如图1(b)所示，在目标点正下方设置一个虚拟目标点，车辆在虚拟目标点的引力下可逃出局部极小值陷阱，然后撤销虚拟目标点. 至此，车辆即可逃出局部极小值陷阱并顺利到达目标点.

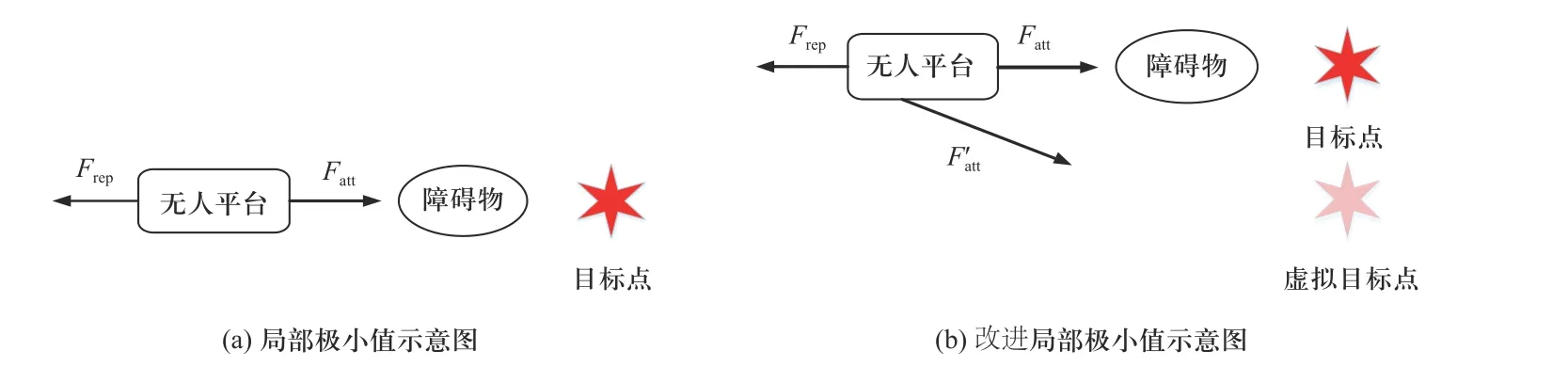
图1 局部极小值工况Fig. 1 The local minimum value case

图2 为局部极小值Matlab 仿真图，图中方块代表无人车，圆代表障碍物，五角星代表目标点. 从图2(a)中可以看出，在传统人工势场法下，车辆运动到距离障碍物和目标点一段距离时便不再运动，陷入局部极小值. 从图2(b)中可以看出,改进的势场法通过增设虚拟目标点，能使车辆跳出局部极小值陷阱并顺利到达目标点.

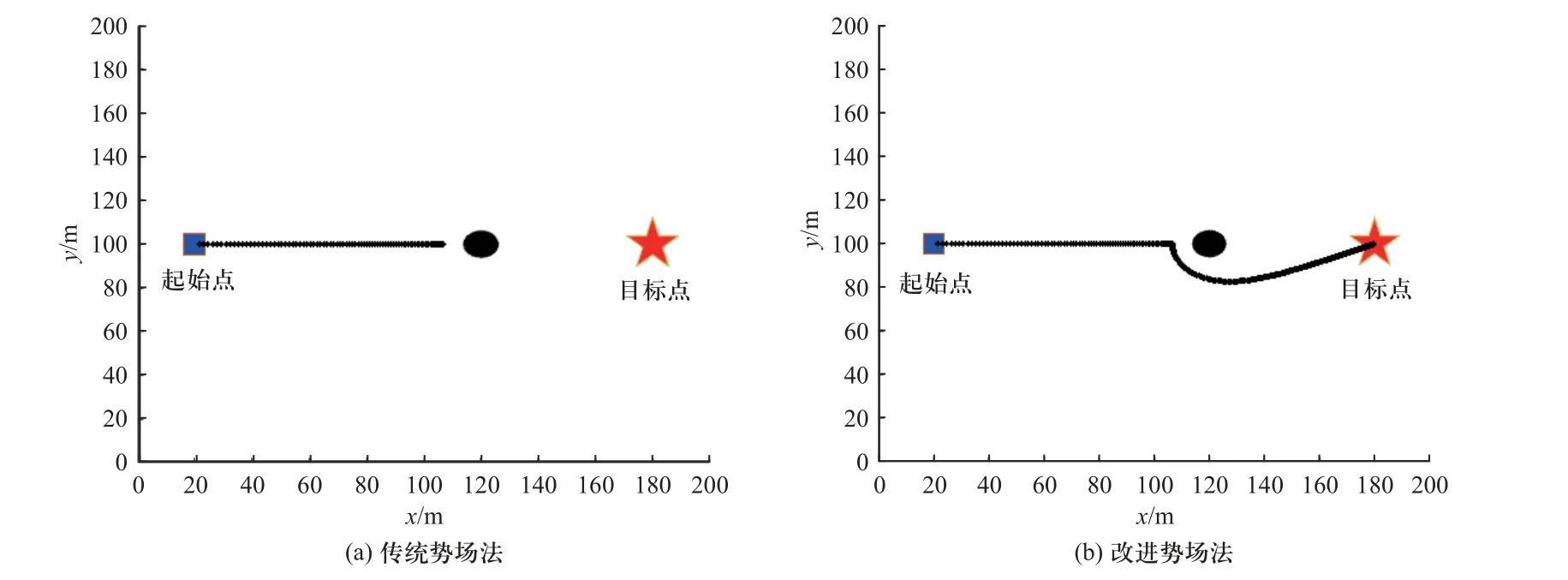
图2 Matlab 仿真图Fig. 2 Matlab simulation diagram

2.1.2 目标点位于车辆和障碍物之间

由于障碍物在车辆运动方向上位于目标点右侧，如图3 所示，车辆必先到达目标点才有可能碰上障碍物，因此当车辆陷入局部极小值时，可通过直接撤销障碍物斥力的方式来使车辆逃出局部极小值陷阱.

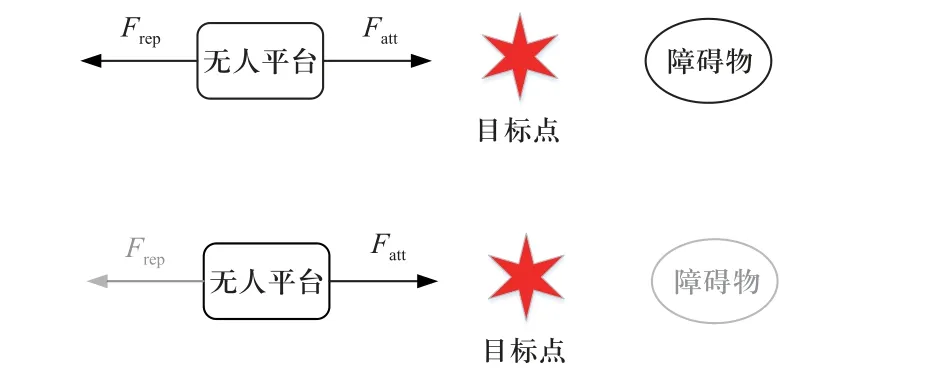
图3 局部极小值工况Fig. 3 local minimum value case when obstacle locates behind target

从图4(a)可以看出，在传统人工势场法下，车辆运动到距离目标点一段距离时便不再运动，陷入局部极小值，无法顺利到达目标点. 而改进的势场法通过撤销障碍物，能使车辆跳出局部极小值陷阱并顺利到达目标点.

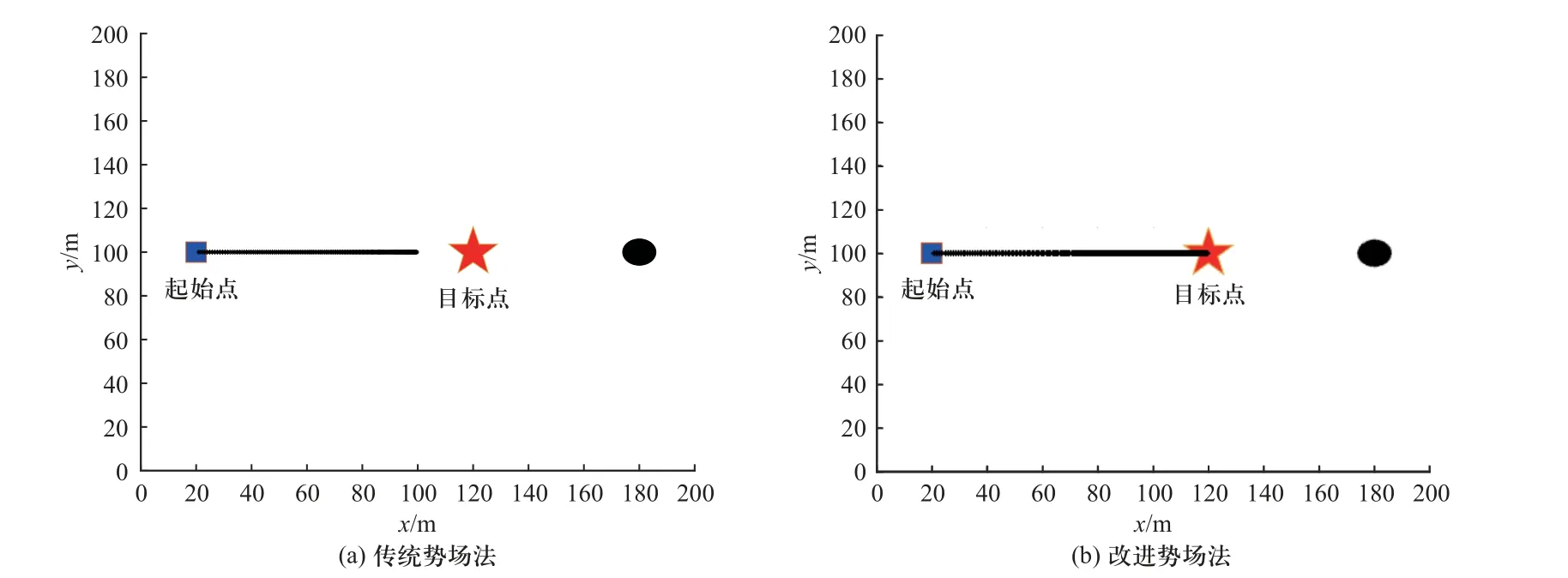
图4 Matlab 仿真图Fig. 4 Matlab simulation diagram for obstacle locates behind target

2.1.3 两个障碍物位于车辆和目标点中间

车辆在障碍物和目标点的共同作用下陷入局部极小值，如图5 所示，与2.1.1 工况类似，不同的是，两个障碍物之间有间距，除去障碍物的影响范围，判断障碍物之间的无影响间距是否满足车辆的安全通过距离Ssafe,若满足车辆的侧向通过安全距离，则通过改进的引力势场函数提高目标点对车辆的吸引力，使得车辆继续沿当前行驶方向前进，直至到达目标点. 改进的势场函数为

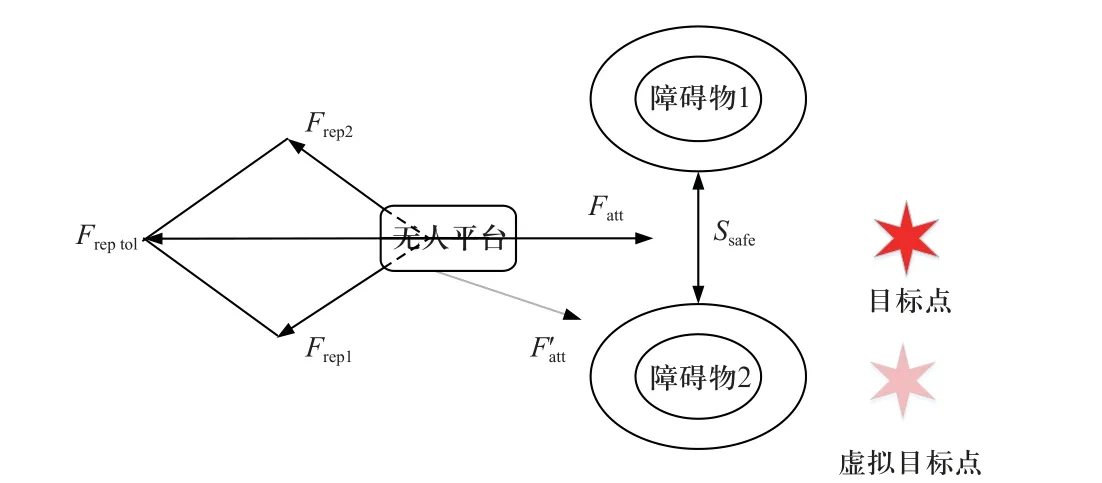
图5 局部极小值工况Fig. 5 local minimum value case when 2 obstacles locate between the vehicle and target

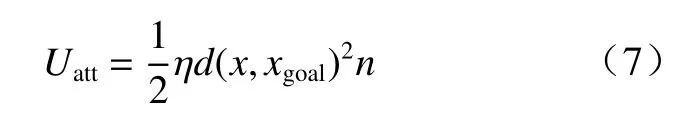
式中：n取决于障碍物的个数，n=i-2；i为障碍物个数，这里i=2.

若障碍物之间的无影响间距不满足车辆的侧向通过安全距离，则采取2.1.1 节的解决方案，在障碍物的下方设置虚拟目标点，使得车辆逃出局部极小值陷阱.

从图6 可以看出，在传统人工势场法下，车辆陷入局部极小值，无法顺利到达目标点. 而改进的势场法通过判断可通行间距，能使车辆选择合适的避障路径并顺利到达目标点.

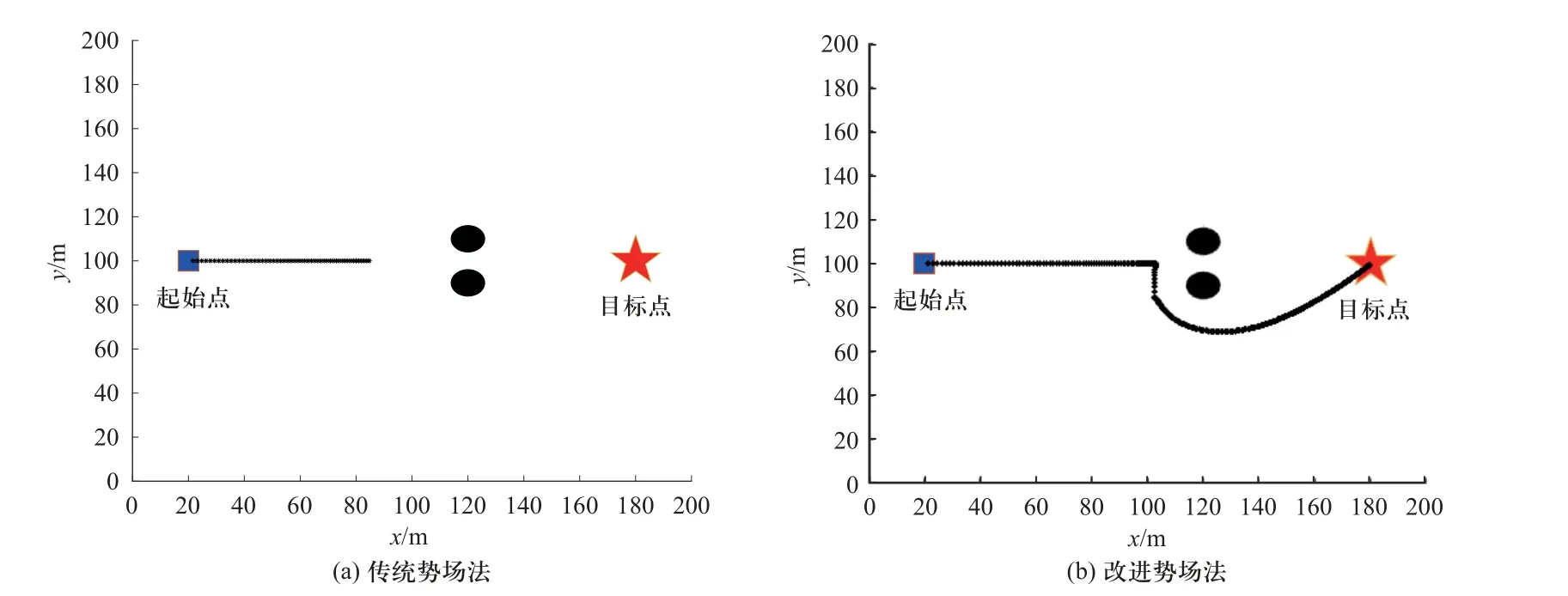
图6 Matlab 仿真图Fig. 6 Matlab simulation diagram for 2 obstacles locate between the vehicle and target

2.2 目标不可达问题改进

目标不可达是指当障碍物出现在目标位置附近时，因障碍物产生的斥力较大，无人车不能顺利到达目标点. 由于障碍物斥力和目标点吸引力的合力与吸引力夹角过大，车辆有偏离目标点的运动趋势，因此无法顺利到达目标点. 如图7(a)所示.

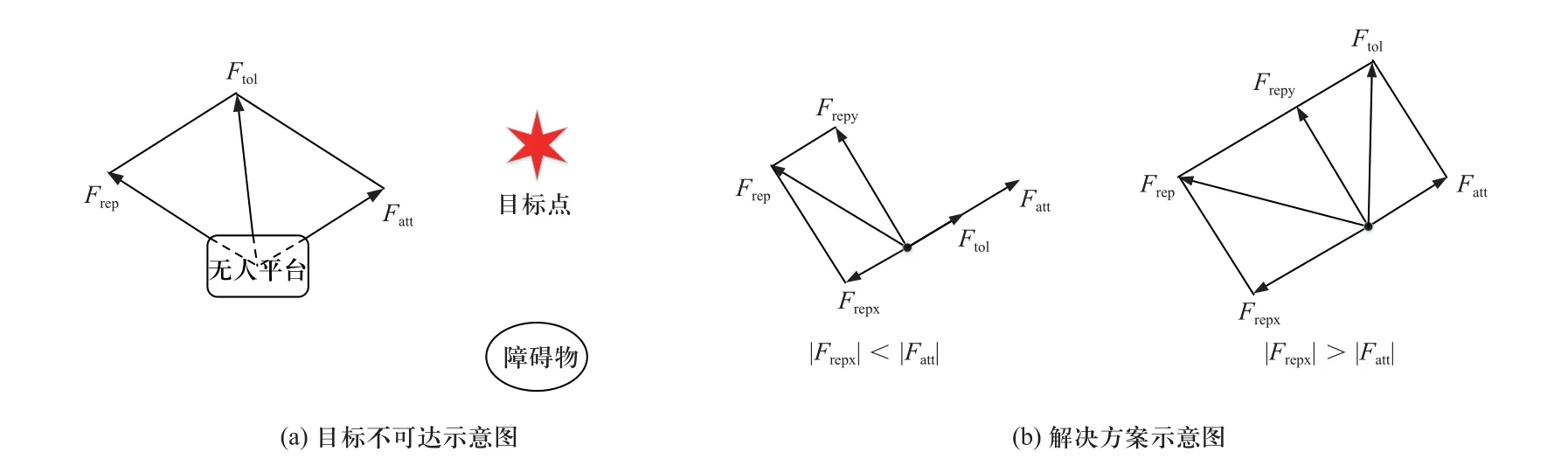
图7 目标不可达工况Fig. 7 Target unreachable condition

将斥力分为引力方向和垂直引力方向两个向量，如图7(b)所示，比较两个斥力分力的大小，若沿引力方向的斥力分力绝对值小于引力，则令垂向斥力为0，即：

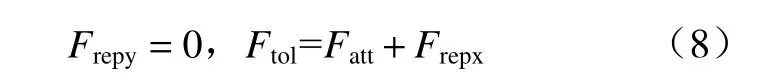
若沿引力方向的斥力分力绝对值大于引力，则令引力方向的斥力分力为0,即：

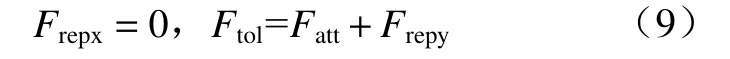
从图8 可以看出，在传统人工势场法下，车辆止步于目标点附近，无法顺利到达目标点. 而改进的势场法能够消除障碍物对目标点附近车辆的影响，使车辆顺利到达目标点.

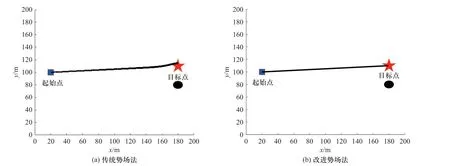
图8 Matlab 仿真图Fig. 8 Matlab simulation diagram for target unreachable condition

3 局部避障路径规划算法

未知环境中可能存在多个未知的移动障碍物，因此要预先对环境中的障碍物进行检测，筛选掉对路径规划无影响的障碍物，然后评估剩余的障碍物对路径规划的影响风险，再进行下一步的规划处理.

3.1 障碍物初筛选

首先建立一条自我车辆到目标点的虚拟直线，记为LST,其表达式为

设障碍物到自我车辆的距离为dobs-ego，障碍物到直线LST的距离为dobs-ST， 当dobs-ego或dobs-ST任意一项小于各自的安全阈值时，就判定其对应的障碍物会对自我车辆后续的路径规划造成影响，从而将这些可能对路径规划有影响的障碍物筛选出来. 这种障碍物预筛选方法忽略了距离较远的障碍物对自身期望轨迹的影响，大大提高了路径规划的效率.dobs-ego和dobs-ST的表达式为

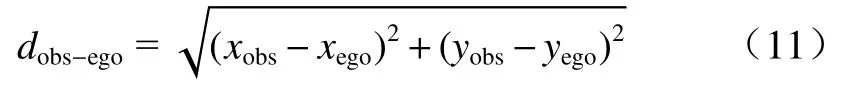
3.2 动态障碍物规划算法

3.2.1 侧向动态障碍物规划

设射线Lobs与线段LST的虚拟交点为P(xP,yP)，其横纵坐标表达式为

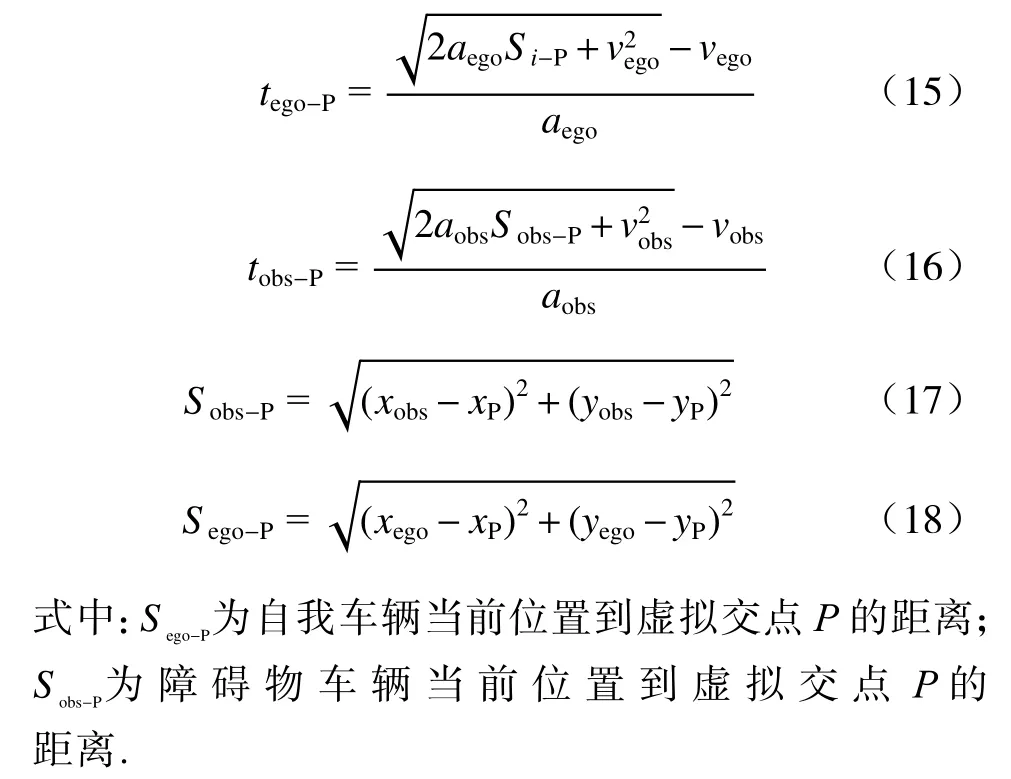
基于虚拟碰撞点P，分别计算自我车辆与障碍物车辆从当前位置到达虚拟碰撞点P所需花费的时间. 设自我车辆当前车速为vego，加速度为aego，障碍物车辆当前车速为vobs，加速度为aobs，二者分别以当前运动状态驶向点P耗时分别为tego-P、tobs-P，其表达式为

对自我车辆和障碍物车辆运动到点P的时间进行比较，若tobs-P＜tego-P,说明障碍物车辆先到达虚拟交点.当障碍物车辆靠近点P且到自我车辆的距离大于安全距离，那么自我车辆将维持原状态行驶. 若障碍物到自我车辆的距离小于安全距离，那么自我车辆就需提前减速甚至制动，以此来规避碰撞的发生. 当障碍物车辆驶离P点后，自我车辆便恢复原始车速驶向目标点. 若tobs-P=tego-P,要根据自我车辆的运动学和动力学约束来判断应采取何种措施来规避碰撞. 以保证行车安全性为前提设置碰撞决策优先级，减速、制动工况优先级高于加速和转向工况优先级. 当存在碰撞风险时，在保证安全距离的前提下，自我车辆首先采取减速措施，若减速后依然未能降低碰撞风险，则采取制动措施来避让障碍物车辆. 待障碍物车辆逐渐远离自我车辆后，自我车辆开始缓慢加速直至恢复到给定车速. 若tobs-P＞tego-P,说明自我车辆会较快到达虚拟交点，若障碍物到自我车辆的距离小于安全距离，自我车辆就会在障碍物斥力作用下脱离直线轨迹以躲避动态障碍物；其次，当自我车辆感知到碰撞风险增加后，其在避让的同时会提高车速，以快速脱离障碍物的影响范围，进一步保障路径规划的安全性. 若障碍物到自我车辆的距离大于安全距离，自我车辆就维持原状态行驶，直至到达目标点.

3.2.2 同向障碍物规划算法

图9(b)所示同向跟车避障路径规划中，无人车需要判断出前方车辆的行驶状态并做出决策：跟车、制动或者转向. 当无人车与前方车辆行驶速度适中且车间距满足安全距离的要求时，无人车保持跟车行驶. 当无人车车速大于前方车辆且车间距小于安全距离，同时无人车侧方存在障碍物且不满足转向要求时，无人车进行制动操作. 当无人车车速大于前方车辆且车间距满足换道间距，同时无人车侧方道路环境满足换道条件时，无人车进行换道操作.

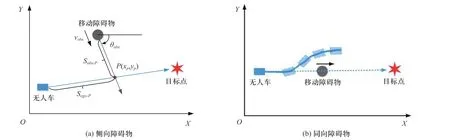
图9 动态规划示意图Fig. 9 Dynamic programming diagram

3.3 路径平滑处理

贝塞尔曲线是描述二维图形的一种数学曲线，主要由顶点和控制点组成，能够利用较少的控制点拟合出复杂的平滑曲线图形.n次贝塞尔曲线表达式为

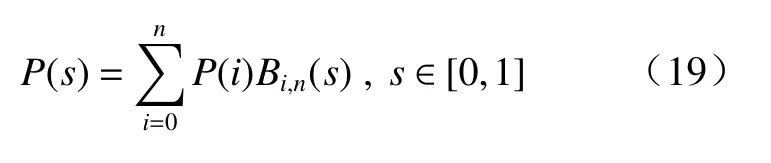
式中：P(s)为控制点;s为变量;P(i)代表位置点;Bi,n(s)为n次伯恩斯坦多项式.

方程中n的含义也可表示贝塞尔曲线的阶数，位置点个数为n+1，控制点个数为n-1.文中采用三阶贝塞尔曲线对局部规划路径进行平滑处理. 路径平滑效果如图10 所示.

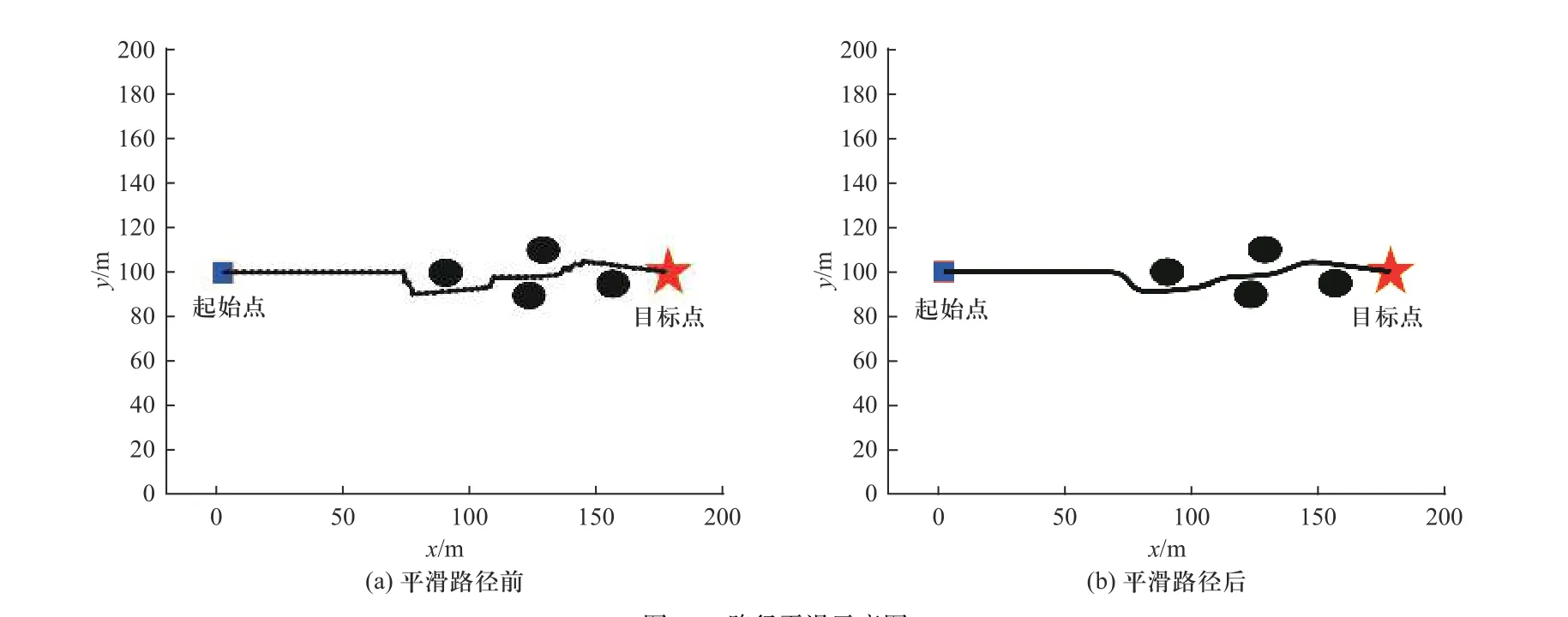
图10 路径平滑示意图Fig. 10 Path smoothing diagram

4 仿真分析

本节对提出的避障算法进行仿真分析. 设定规划空间为200 m×200 m 的二维大地坐标系. 起始点坐标为(20, 100),目标点坐标为(180, 100). 障碍物为半径7 m 的圆，大方块代表无人车，五角星代表目标点，小方块前方线段为每个规划周期的规划路径. 规划算法仿真完毕后，在Carsim-Simulink-Prescan 联合仿真平台中验证规划路径的有效性和可跟踪性.

4.1 工况1∶侧向动态障碍物

圆形障碍物速度设置为5 m/s，方向沿y轴负方向，无人车速度设置为10 m/s. 车辆的动态规划路径如图11 所示，无人车能够提前决策并躲避侧向障碍物，规划的路径平滑合理.

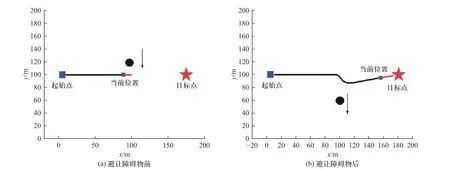
图11 侧向避障过程示意图Fig. 11 Schematic diagram of the lateral obstacle avoidance process

4.2 工况2∶同向动态障碍物

圆形障碍物速度设置为5 m/s,方向沿x轴方向，无人车速度设置为10 m/s.车辆动态规划路径如图12所示，无人车在完成超车变道后能回归原行驶车道并顺利到达目标点.

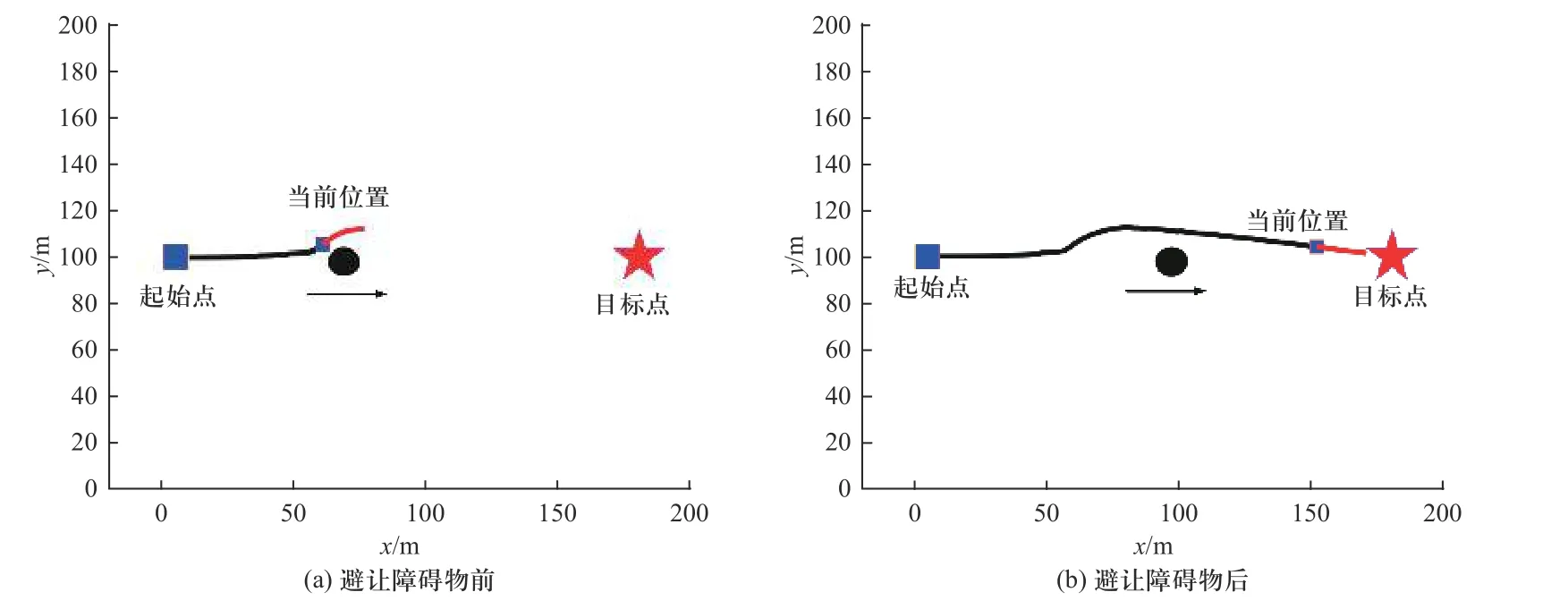
图12 同向避障过程示意图Fig. 12 Schematic diagram of the same-direction obstacle avoidance process

4.3 工况3∶复杂动态障碍物

针对侧向和同向均有动态障碍物的工况，融合两种工况的规划算法，仿真结果如图所示. 两个圆形动态障碍物速度均为5 m/s，移动方向分别为y轴负方向和x轴正方向. 无人车速度为10 m/s.车辆的规划路径如图13 所示，对于侧向和同向均有移动障碍物的工况，无人车能够预先做出决策并规划出一条无碰撞路径，顺利到达目标点.

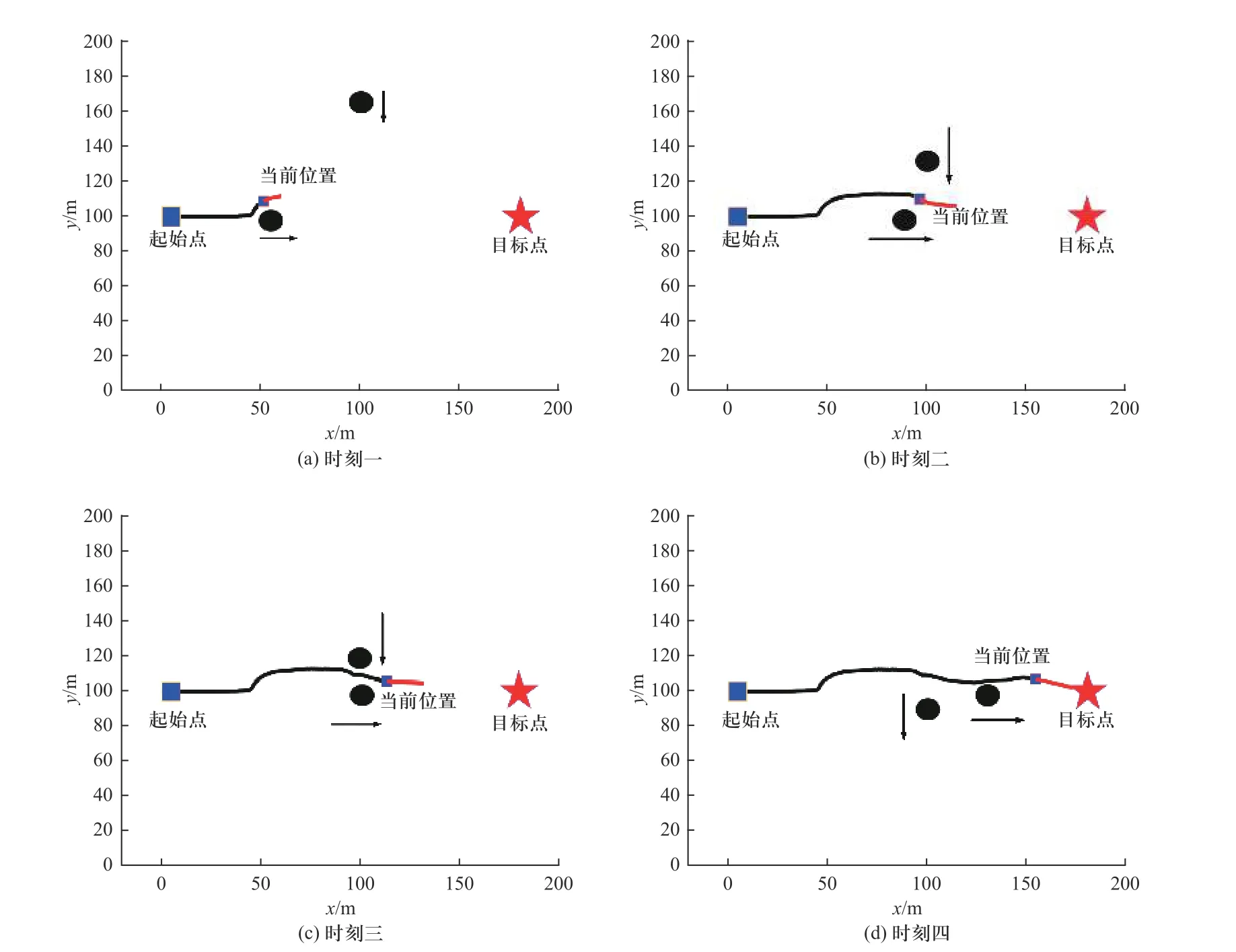
图13 复杂避障过程示意图Fig. 13 Schematic diagram of complex obstacle avoidance process

4.4 联合仿真平台

在Prescan 中搭建如图14 所示的仿真道路环境，设置字路口侧向障碍物车辆速度为20 km/h，斑马线行人速度为1.1 m/s，设主车初始车速为0，加速度为2 m/s2，一般制动减速度为2 m/s2，紧急制动减速度为6 m/s2. 行人与侧向来车为主车前进道路中的动态障碍物. 传统人工势场法规划出的轨迹如图15 所示，自主车辆未能及时对侧向动态障碍物进行避让，在45 m 处与行人发生了碰撞，感知系统检测到碰撞后自动终止仿真. 图16 为改进人工势场法的规划轨迹与跟踪效果，由路径跟踪曲线可知，车辆轨迹在45 m处和70 m 处有些许偏差，原因为避让行人和侧向来车. 总体上规划的路径能满足车辆动力学要求，跟踪性能良好. 由速度跟踪曲线可知，车速两次大的波动分别出现在减速避让行人(10 s 处)和加速通过十字路口(15 s)处，与路径规划结果相对应，速度规划满足车辆跟踪要求.

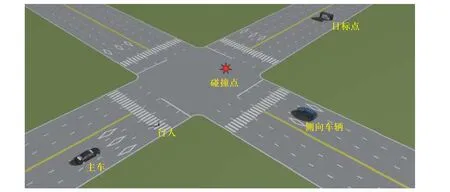
图14 十字路口虚拟道路环境Fig. 14 Crossroads virtual road environment

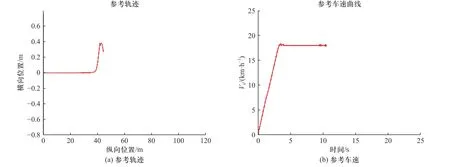
图15 传统人工势场法仿真结果（发生碰撞）Fig. 15 Simulation results of traditional artificial potential field method (Collision)

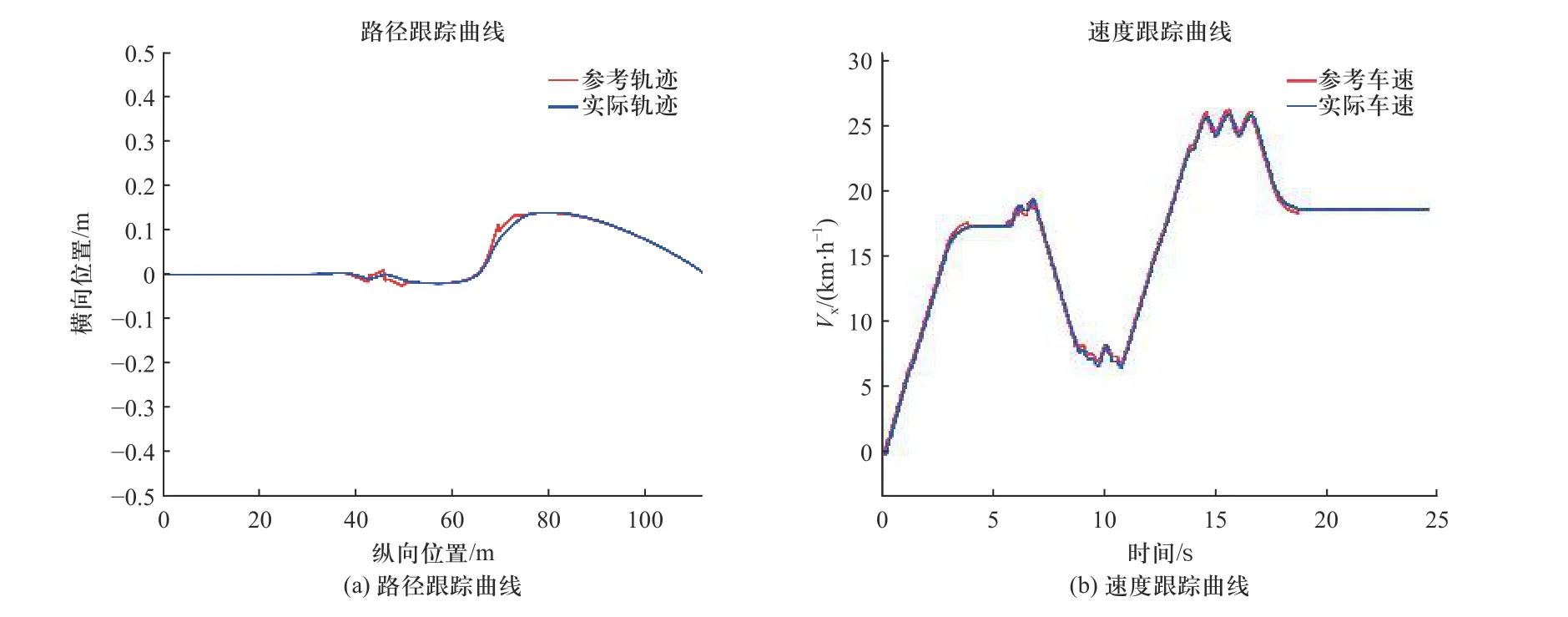
图16 改进人工势场法仿真结果Fig. 16 Improved artificial potential field method simulation results

表1 为两种人工势场规划算法实时性仿真数据统计，传统人工势场法仿真时自主车辆发生碰撞，未能完成完整路径规划，因此仿真时间截止到10.5 s.在仿真实验中，Matlab 工作平台处理器为i7-6700@3.40 GHz，CPU 的计算时间通过Matlab 指令来获取.由表1 可知，传统人工势场算法单步仿真时间为系统仿真步长的13.1%，而改进后算法为15.7%. 改进人工势场法在大幅提高算法规划能力的同时，仍具备良好的实时性.

表1 算法仿真实验数据Tab. 1 Algorithm simulation experimental data

5 结 论

针对无人车行驶环境的复杂性和未知性，文中对道路环境中的静态障碍物和动态障碍物进行无人车局部避障规划算法研究. 在传统人工势场法的基础上建立行车风险场，针对静态障碍物，提出解决局部极小值和目标不可达问题的算法，以有效解决势场法避障规划的缺陷；针对动态障碍物，实时采样获取其运动方向和运动速度等参数，设置碰撞决策优先级，对侧向及同向动态障碍物两种运动工况提出局部避障规划模型，并对规划路径进行平滑处理. 联合仿真结果表明，文中提出的局部避障规划算法能使无人车在复杂环境下顺利躲避动静态障碍物，且规划算法计算量小，规划的路径实时性和平顺性较好，符合车辆运动学和动力学性能要求.