“双管齐下”，求圆锥曲线的离心率

杨宪伟

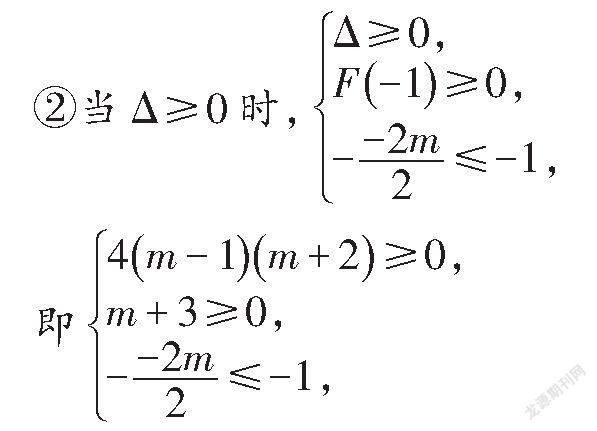
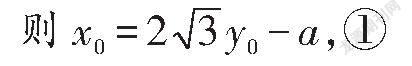
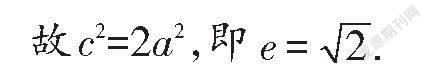
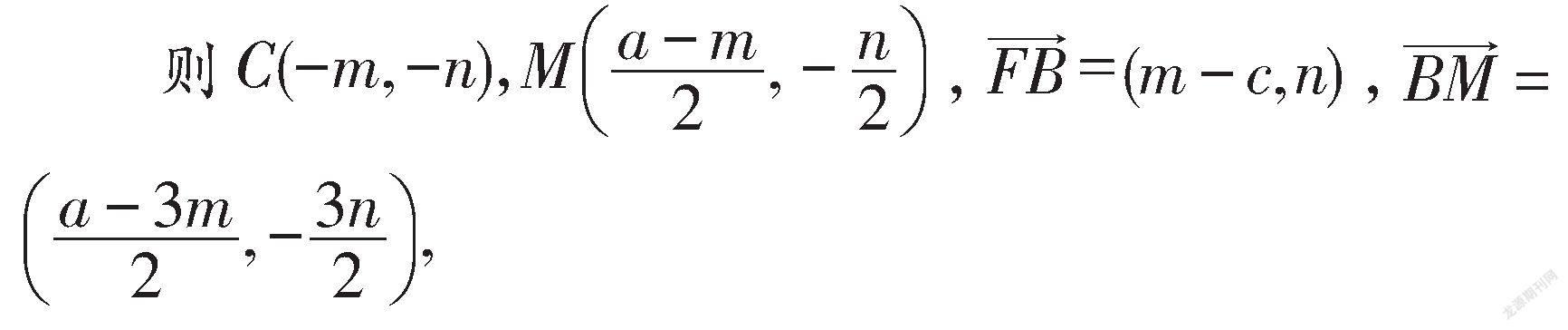
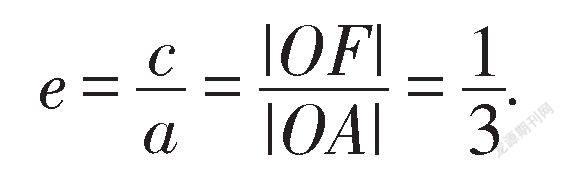
1.代数法

代数法是指从圆锥曲线的方程出发，通过代数运算求得a、c的值或其关系式，从而求得离心率e.运用代数法求圆锥曲线的离心率，需根据题意和圆锥曲线的方程，建立关于a、b、c的关系式，再根据椭圆、双曲线中a、b、c的关系求得圆锥曲线的离心率.

2.几何法

几何法是根据圆锥曲线的定义、几何性质、平面几何图形的性质来解题的方法.在运用几何法求圓锥曲线的离心率时，要通过分析图形，发现一些几何关系，如平行关系、垂直关系、线段的相等、半、倍关系等，然后利用三角形中线的性质、相似三角形的性质、直角三角形的性质、圆锥曲线的定义、几何性质求得椭圆或者双曲线的半焦距、长半轴长、实半轴长及其关系式，最终求得圆锥曲线的离心率.

解法一（代数法）：由题意可知F（c，0），A（a，0），设B（m，n），

因为F，B，M三点共线，

所以n（a-3m）=-3n（m-c），即a=3c，

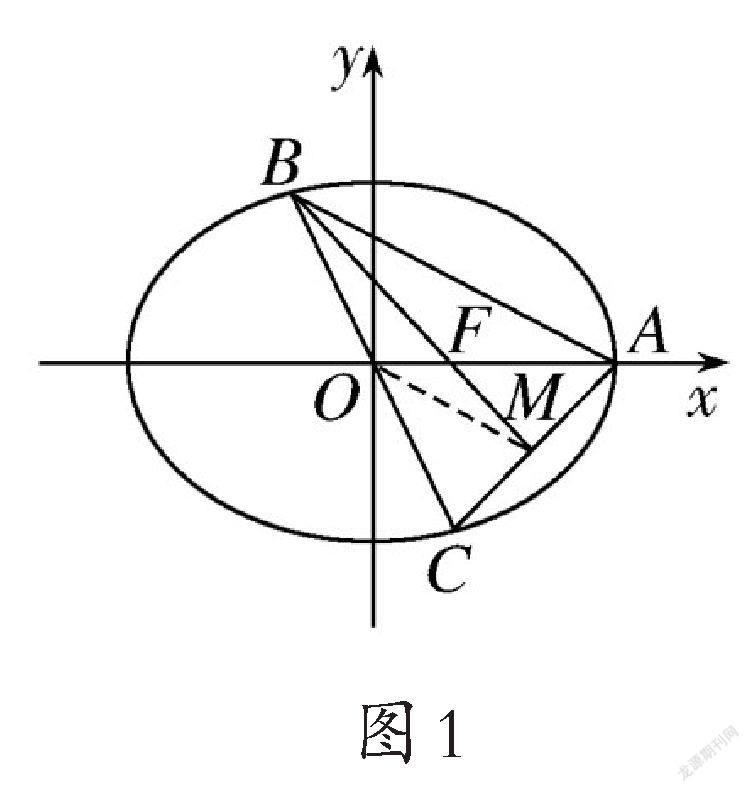
解法二（几何法）：如图1，设点M为AC的中点，连接OM，则OM为△ABC的中位线，所以椭圆的离心率

解法一是借助向量的共线定理来建立之间的关系式，通过代数运算求得椭圆的离心率.解法二是利用了三角形的中位线的性质，借助图形，建立椭圆长半轴长、半焦距之间关系，求得问题的答案.

解法一（代数法）：由题意可得F（c，0）

设A为线段OF的垂直平分线与x轴的交点，

则a-b=36，

可得a-85a+324=0，解得a=81或a=4（舍去），

解法一是根据题意建立关于a、b、c的方程组，通过解方程求得a、c的值.解法二是通过添加辅助线，利用勾股定理和垂直平分线的性质寻找到有关椭圆长半轴长、半焦距的几何关系，从而运用几何法求得问题的答案.

解法一（代数法）：由题意可知A（-a，0），设P（x，y），

而△PFF为等腰三角形，∠FFP=120°，

由①②③可得：a+4ac-32c=0，

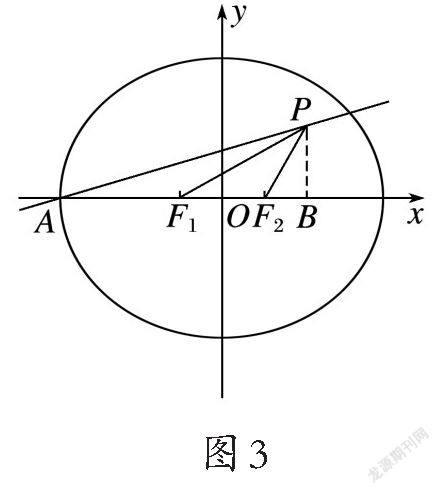
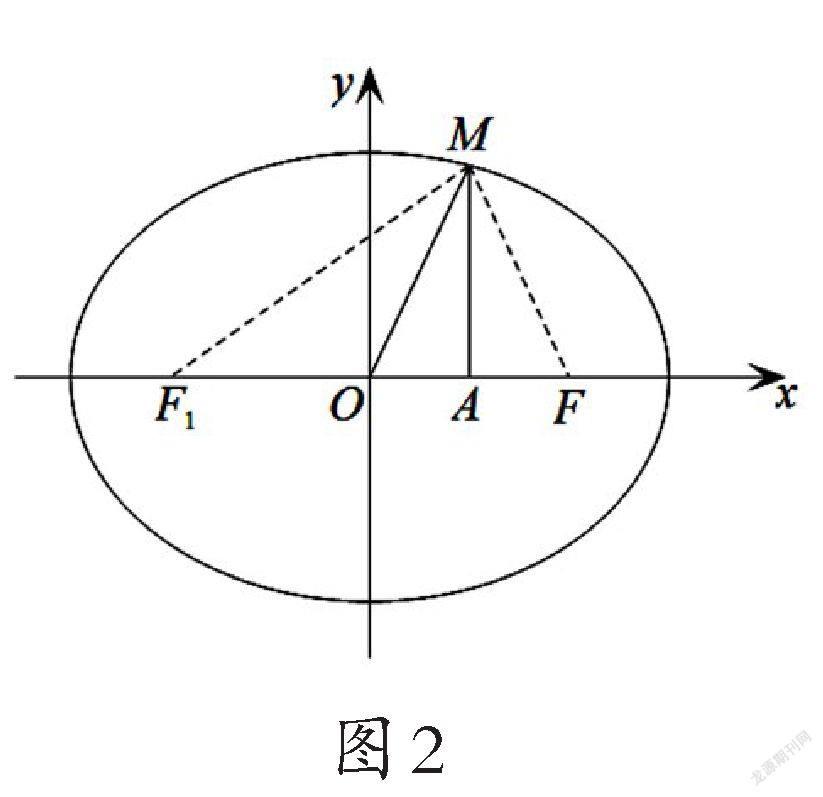
解法二（几何法）：如图3，作PB⊥x轴于点B.

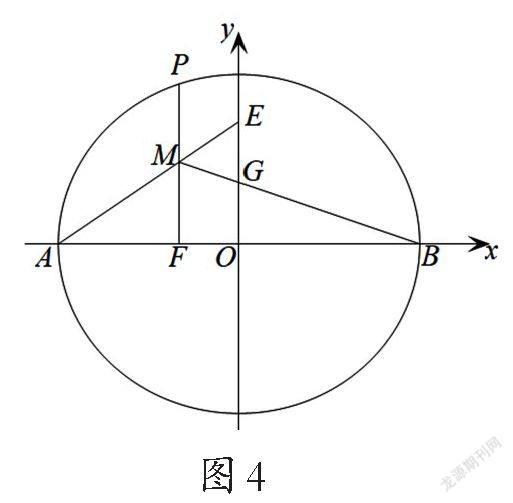
解法一（代数法）：由题意可知A（-a，0），B（a，0），

设G（0，m），则E（0，2m），则直线BM的方程为：

解法一是根据两条直线的方程建立关于a、c的方程组，通过代数运算求得e的值.解法二是根据几何图形的特点，寻找到相似三角形，利用相似三角形的性质建立几何关系，求得椭圆的离心率.

解法二（几何法）：由圆的几何性质可知，△POQ是等腰直角三角形，

解答本题，可以通过联立曲线的方程进行求解，也可构造等腰直角三角形，利用等腰直角三角形的性质来求解.

我们可以看到，运用代数法和几何法求圆锥曲线离心率的思路完全不同.利用代数法解题，关键要建立关于a、c的关系式，可借助向量、构建方程组、构造二次齐次式等方式来建立关系式.运用几何法解题，需先画出图形，明确椭圆或者双曲线的半焦距、长半轴长、实半轴长及其与三角形、矩形、平行四边形等几何图形的位置关系，再利用平面几何知识来求解.相比较而言，几何法较为简单，但通常要添加合适的辅助线，运用代数法求解的运算量较大，但其思路较为简单.同学们可根据解题需求和自己熟悉的知识点选择最佳的方案进行求解.