沥青路面振动碾压施工的数值仿真与工艺参数分析

周刚，但汉成，山宏宇，杨冬，郑仕跃

(1.中海建筑有限公司，广东 深圳 518057；2.中南大学 土木工程学院，湖南 长沙 410075)

路面施工质量影响路面使用性能，而压实作为路面施工过程中的最后一道主要工序，极大程度地影响路面的耐久性[1−2]。压实良好的路面具有较好的平顺性，密实的面层结构可以防止水分经过路面渗入路基，从而保证路基路面结构的稳定[3]。路面压实不足，则会引起路面车辙、剥落和水损害，而路面过压则会引起集料破碎，导致路面混合料级配结构遭到破坏，强度、刚度等性能下降[4−6]。因此，对路面碾压过程进行合理控制，保证路面沥青混合料在施工过程中得到有效和充分压实，从而提高路面的使用质量。实际路面压实施工过程中，压路机作为移动振动荷载完成碾压作业。目前大多数关于路面压实施工工艺的研究均基于施工经验开展，存在科学依据不足的问题，使得压实工艺的制定没有针对性，可能会增加碾压能耗或者压实达不到最佳效率。因此，需要更进一步研究路面振动压实过程中路面的动力响应与施工工艺参数。目前研究路面在动荷载作用下的动力响应问题通常有理论解析法和数值模拟法[7−14]。理论解析法通常关注于沥青路面在移动荷载作用下的动力响应问题，把沥青路面看作弹性材料，而振动压实过程中沥青混合料为高温黏弹塑性，因而理论解析法很难准确计算路面结构在振动碾压荷载作用下的动力响应。此外，道路工程中常用到的数值模拟方法主要有离散元法和有限元法。离散元法将混合料离散成不同形状大小的颗粒，通过颗粒之间相互作用属性来研究材料的力学特性，但是由于路面振动压实模型较大，对应的离散元模型通常包含大量颗粒，导致计算效率较低[15]。有限元作为经典有效的数值模拟方法，具有更大的计算效率以及更合理的材料本构模型，从而成为研究沥青路面振动压实过程中路面结构动力响应的主要方法。本文采用ABAQUS有限元软件建立沥青路面下面层振动压实过程的有限元模型。然后，通过有限元模拟计算得到振动压路机作用下路面应力及加速度时程数据，并与现场实测数据进行对比，验证模型的准确性。最后，分析振动压实过程中路面结构在压路机荷载作用下的动力响应规律，并综合对比不同工况条件下路面沥青混合料的力学特征和压实效果，提出沥青路面振动压实参数组合。

1 路面振动压实有限元模型

1.1 路面材料参数

振动碾压试验依托于某高速公路沥青混合料下面层施工进行。该高速公路设计路面结构及材料如图1所示，下面层采用AC-25沥青混凝土，空隙率为4%，其级配如图2所示。

图1 现场试验路面结构图Fig.1 Schematic diagram of pavement structure

图2 下面层AC-25级配曲线Fig.2 Gradation curves for AC-25 asphalt mixture

下面层沥青混合料采用弹塑性本构模型，其抗剪强度遵循摩尔−库伦准则[16]，

式中：A，B，C，D，a，b，c和d为计算参数；T为沥青混合料温度，℃。

沥青混合料的模量表征材料抵抗压缩变形的能力，本文利用沥青混合料多功能综合试验机(UTM)进行单轴压缩试验，获得AC-25沥青混合料在不同温度条件下弹性模量值，如表1所示。

表1 AC-25单轴压缩试验结果Table 1 Test results of uniaxial compression experiment

通过对各个温度下的沥青混合料的弹性模量进行拟合，得到不同温度下AC-25的弹性模量预测公式如式(3)所示：

式中：T为沥青混合料的温度，℃。

通过式(1)～(3)可以得到在高温压实条件下沥青混合料的弹塑性参数(压实实测温度为140℃)，为数值计算奠定基础(表2)。

表2 AC-25沥青混合料材料参数Table 2 Material parameters of asphalt mixture AC-25

基层及土基材料采用线弹性本构模型，各材料参数如表3所示。

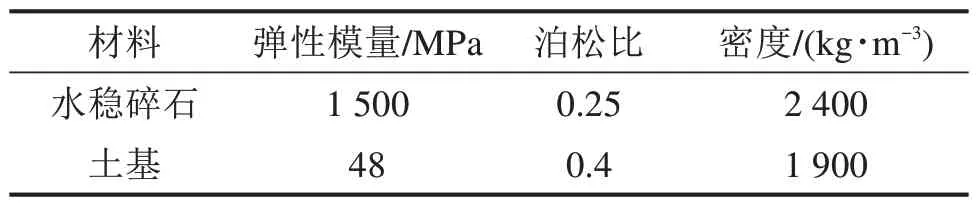
表3 路面基层及土基材料参数Table 3 Material parameters of base course and subgrade

路面结构振动碾压数值计算采用ABAQUS有限元软件进行建模，路面长度10 m，宽度6 m，深度3 m，并在结构各个边界面施加相应的约束条件(路面纵向前后两面采用XSYMM条件、左右两面采用ZSYMM条件、路面底部采用ENCASTRE条件)。建模完成后，对路面结构采用结构技术(structure)进行网格划分，单元类型采用C3D8R(八结点六面体线性缩减积分单元)，共计50 400个单元。路面振动压实有限元模型如图3所示。

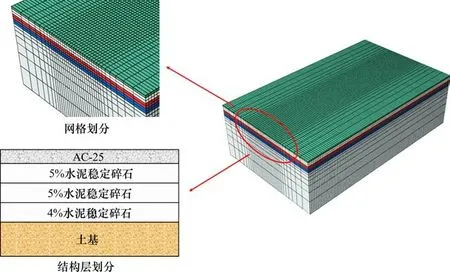
图3 沥青路面振动压实三维有限元模型Fig.3 Three dimensional finite element model for vibration compaction of asphalt pavement

1.2 振动碾压荷载的实现

现场试验过程中采用戴纳派克(Dynapac CC6200)双光轮振动压路机，其工作参数列于表4。

表4 Dynapac CC6200振动压路机工作参数Table 4 Working parameters of vibratory roller

振动压路机工作过程中，采取后轮滚动前轮振动的方式，振动轮作用于路面结构的荷载形式为简谐振动，采用正弦函数：

式中：F0为压路机产生的激振力；F0=Meω2；Me为偏心块偏心力矩；ω为正弦函数的圆频率，ω=2πf。

在有限元计算时将振动轮轴重(G)与简谐振动的激振力(P)一并施加于路面结构层，即：

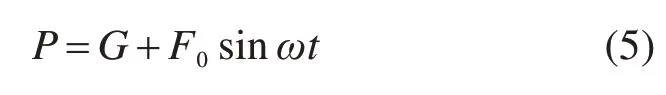
振动压路机在工作过程中，振动轮旋转产生的激振力F0通常大于轮重，甚至是轮重的2～3倍。在路面振动压实过程中，压路机对路面沥青混合料只能够施加压力作用，因此，压路机振动过程中激振力形式可以进一步表示为：

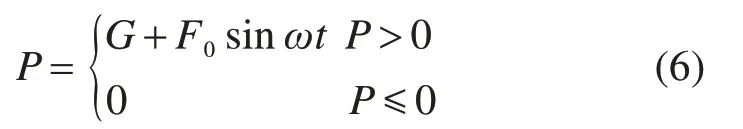
压路机荷载采用压力荷载形式，其接触应力大小根据支喜兰等[17]给出压路机荷载的分布计算公式如下：

式中：D为振动轮直径，取1.2 m；L为振动轮宽度，取2.1 m。

将式(5)，式(6)代入式(7)，可得：

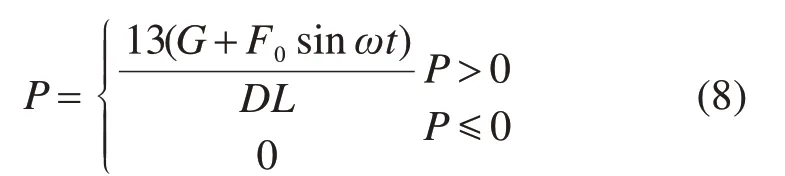
分析压路机荷载振动作用下路基路面结构受力情况时，压路机振动轮与路面接触面可看成矩形，荷载面积为0.2 m×2.1 m。

依据现场实际路面振动碾压过程中所选择的压路机振动频率，在进行有限元计算时，取67 Hz作为主要计算工况进行加载，相应激振力为106 kN，现场压路机工作速度为4 km/h。由于模型为非线性计算，为提高计算效率，荷载移动距离设置为8 m(即荷载移动带长度为8 m)，利用Fortran语言将式(8)所表示的荷载形式编写为DLOAD用户子程序实现振动碾压过程。图4为压路机荷载作用于路面有限元模型示意图。

图4 有限元模型中振动碾压荷载示意图Fig.4 Schematic diagram of vibration rolling load in finite element model

2 路面振动压实有限元计算结果分析

2.1 有限元计算结果

通过有限元计算，得到在压路机振动荷载作用下的路面压实轨迹中点处面层结构接触应力和加速度如图5所示。

图5 振动碾压条件下路面振动响应随时间变化Fig.5 Vibration response of road surface varies with time under vibration rolling condition

将有限元计算得到的路面结构理论动力响应与现场实测数据对比如图6所示，试验测试方案设计如图7所示。试验过程中测点前后12 m设置为数据采集区域：当振动压路机进入采集区域时，开始记录智能颗粒及振动轮加速度响应数据直至压路机驶离采集区域后停止记录。沥青混合料摊铺完成后，采用双光轮振动压路机进行振动碾压6遍，随后采用轮胎压路机进行终压。现场试验中路面及振动轮的振动信号数据分别由智能颗粒WDQ1及HCF传感器获取。通过图6可以看出，理论数据与计算数据吻合较好，其中路面实测加速度大于有限元计算加速度，这是由于现场压实过程中，有多台压路机协同工作，且同时还有摊铺机等施工器械，测点附近一直有较强烈的振动荷载经过，导致对现场实测路面加速度产生一定影响。

图6 有限元计算加速度与现场实测加速度对比Fig.6 Comparison of the acceleration calculated by finite element with the field measurement

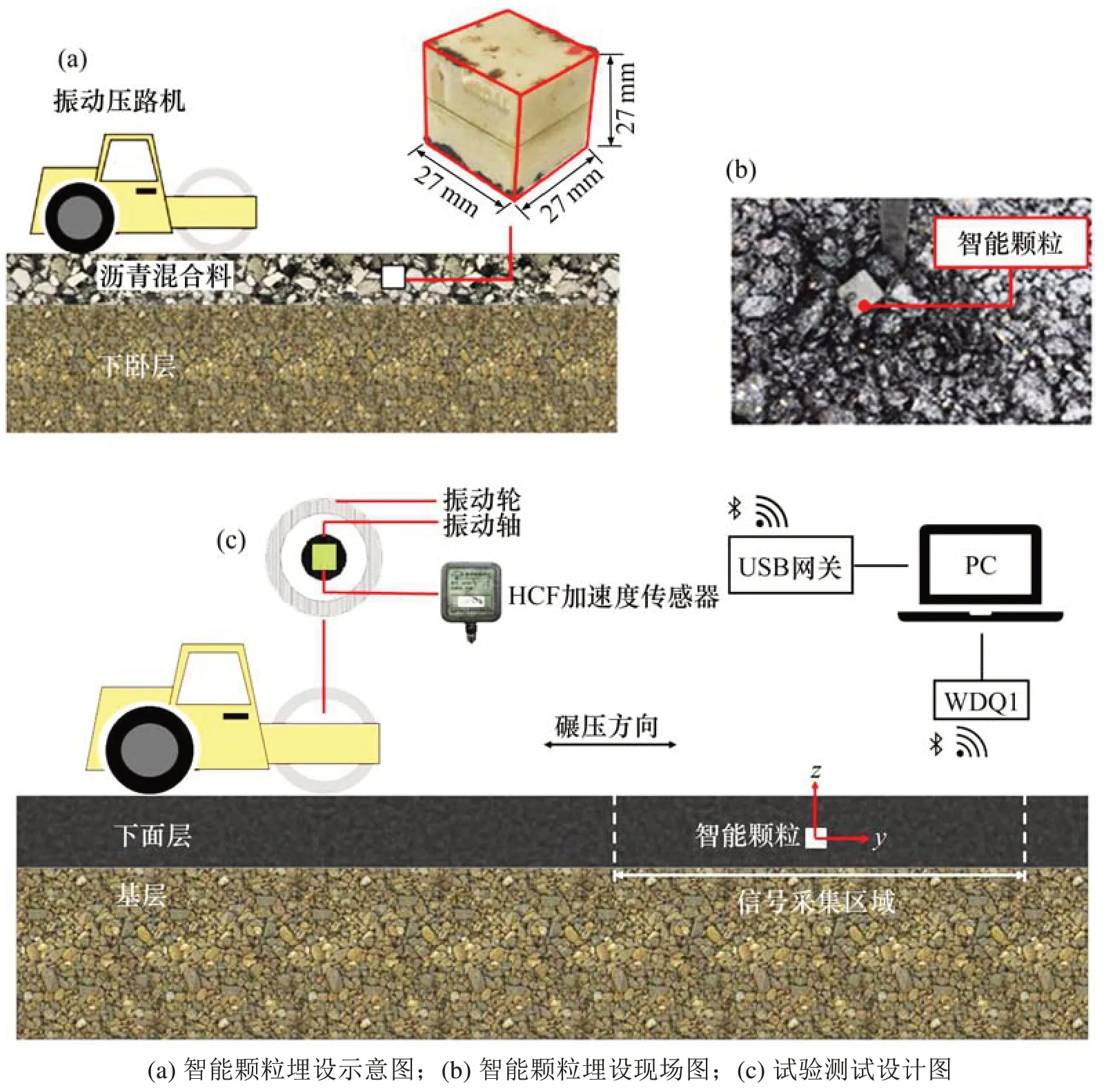
图7 智能颗粒测试路面振动加速度Fig.7 Pavement vibration acceleration tested by SmartRock

2.2 振动压实过程路面应力响应规律

沥青路面振动压实过程中，振动轮与路面直接的作用力大小将直接影响到路面沥青混合料的压实效果。图8为沥青路面振动压实过程中在压路机碾压至2.8 s时路面结构所受到应力云图。可以看出，在压路机作用下，路面所受到的应力并非均匀分布。在垂直于路面碾压方向上，振动轮左右两侧与路面接触应力较小，中部较大；在路面碾压方向上，接触应力同样呈现出“中间大，两边小”的分布规律。

图8 振动压实过程中振动轮与路面接触应力Fig.8 Contact stress between vibration wheel and road surface during vibration compaction

将压路机振动荷载作用区域横向与纵向各个节点的应力值输出，并绘制应力大小分布图如图9所示。可以看出，压路机施加于路面的作用力大小呈现出较好的对称性。在横向上，振动轮边缘两侧作用力为0.03 MPa，从两侧向中间逐渐增加，在距离振动轮中心0.4 m时应力达到最大值0.69 MPa并最终稳定在该应力值左右；在碾压方向上，在压路机与路面接触区域内的应力值均稳定在0.69 MPa附近。此外，通过图9(b)可以看出，振动压路机荷载除了对其直接作用于路面区域内有压实作用，而且其影响范围可以扩展至振动轮中心处前后0.3 m。

图9 压路机作用下路面应力分布图Fig.9 Pavement stress distribution diagram under roller action

同样，可以根据有限元计算结果研究路面振动压实过程中压路机压实作用力在路面结构的影响深度范围。图10(a)同样是在计算至2.8 s时将路面沿中部分割后的应力分布云图。可以看出，压路机荷载中心处的应力除了作用于面层结构外，还向下延续至其他结构层内。将振动荷载中心下各个距离处的应力数值绘制分布图如图10(b)。可以看出，随着路面深度的增加，路面内部应力先是以较快的速度减小，当深度达到0.45 m左右时，压应力大小从0.69 MPa减小至0.15 MPa，随后应力值随深度变化的速率减小，并在深度达到2.6 m左右时应力值减小至0 MPa左右，即在压路机工作频率为67 Hz，激振力为106 kN时，压实力的压实作用最大深度可达路面结构层2.6 m左右。

图10 压实应力沿深度方向分布图Fig.10 Distribution diagram of compaction stress along the direction of depth

3 路面碾压参数及工艺分析

3.1 振动频率分析

振动频率是路面压实过程中压路机重要的工作参数，不同的工作频率对应振动压路机会产生不同的工作振幅和激振力，从而影响路面压实效果。为了研究振动压路机在不同工作频率碾压下路面的动力响应及压实效果，依据选用的戴纳派克振动压路机参数，计算对比在相同工作速度下路面结构分别在51 Hz和67 Hz工作频率及对应的激振力条件下的面层应力时程曲线如图11(a)，通过压路机振动轮压实应力沿路面结构深度方向的分布规律可以看出，压实应力延伸度方向的变化斜率可以分为2个阶段，即迅速减小阶段和缓慢减小阶段，因此可以定义第1阶段与第2阶段交点处的深度值作为压实力的有效作用深度(图11(b)、图11(c))，由于压实过程中沥青混合料主要表现为塑性，可以将压实过程中混合料的累积塑性应变(即等效塑性应变，PEEQ[18])作为混合料压实效果的评价因素。图11(d)列出了在不同频率工况下，振动轮中心点作用下路面结构路面沥青混合料面层应力及平均等效塑性应变。

图11 不同频率下路面动力响应Fig.11 Dynamic response of pavement at different frequencies

通过对比可以看出，在相同的工作速度下，低频条件下路面所受到的最大压应力与等效塑性应变均相比于高频工作条件下路面所受压应力与压实后的等效塑性应变分别增加了26%和217%，低频率下的压实力的有效作用深度相比高频率条件下增加了95%。这是由于低频率对应更高的激振力作用，高温下沥青混合料模量低，抗剪强度低，在较大的压应力作用下能够更快速达到屈服并产生较大的塑性变形。另外，通过图11(b)可以看出，当材料力学性能相同时，压实力沿深度方向传递速率相同，不同深度处的数值大小取决于压路机所施加的压实力大小。

在路面压实施工过程中，采用较大的激振力可以明显地提高路面沥青混合料的压实效果，但是在压实后期过大的压实力作用将导致混合料集料振碎等问题，导致路面受力特性改变，从而影响路面的使用质量。因此，结合不同频率下的路面沥青混合料等效塑性应变以及理论分析结果对比，在压实初期，由于沥青混合料较为松散且阻尼较大，可以采用“低频高幅高激振力”的参数组合(51 Hz，0.8 mm，194 kN)，从而能够使混合料快速形成具有一定密实度的骨架结构；而在中后期的压实中，混合料刚度较大阻尼减小，因此可以选择“高频低幅低激振力”的参数组合(67 Hz，0.3 mm，139 kN)，避免过大的压实力导致混合料破碎以及下卧层被振松等现象，保证路面使用性能。

3.2 碾压速度分析

振动压路机进行振动碾压时行走的速度称为压路机的工作速度，路面沥青混合料振动压实过程可以分为初压和复压2个阶段，压路机每个档位的工作速度分别为2～3 km/h(1档)、4～6 km/h(2档)和8～9 km/h(3档)。考虑振动压路机在67 Hz的振动频率下，分别以2，4和8 km/h 3种碾压速度工作时路面表面应力时程曲线对比如图12。

图12 不同碾压速度下路面应力时程曲线Fig.12 Time-history curve of pavement stress under different rolling velocities

通过图12可以看出，不同碾压速度条件下压路机对路面所施加的压实应力大小均在0.9 MPa左右，即碾压速度不会影响压路机的压实力作用。值得注意的是，在较小的碾压速度下路面中点处所受到最大压实应力作用时间大于低速碾压条件下的时间。通过应力时程曲线可以看出，当压路机即将行驶至路面中点处时，由于滚轮的揉搓作用，该位置出现一定程度的隆起，进而产生一定大小的拉应力，随后测点处出现较为明显的压应力作用。为进一步研究，将压路机通过测点前拉应力消失压应力出现至驶过测点后压应力消失拉应力出现这一时间段定义为压实力的有效作用时间。对比不同碾压速度下的压实力有效作用时间与面层等效塑性应变如图13。

图13 不同碾压速度下压实有效作用时间及等效塑性应变Fig.13 Effective action time and equivalent plastic strain at different rolling velocities

对比结果表明，随着压路机工作速度的加快，路面沥青混合料碾压过后的等效塑性应变有所减小。在相同压路机振动频率下，在1档工作速度时，路面的等效塑性应变为0.12，相比8 km/h时增加200%；相应地，1档工作速度下压实力的有效作用时间相比8 km/h时增加207%。可以看出，碾压速度对路面压实效果的影响直接体现在压实力所作用于路面的有效压实时间。此外，压路机移动速度越慢，通过路面结构的时间越长，压路机振动力作用次数越多，产生的能量越大，路面沥青混合料所受到的碾压作用更为充分，从而压实效果更好。因此，在路面压实过程中，需要根据不同的压实阶段选择不同的压实速度：在压实初期，压路机应选择较低挡位的工作速度，以便控制沥青混合料的整体压实效果。由于压路机长时间低速工作会造成机械使用和施工效率降低，因此，在初压后的压实过程中，考虑到压实效果以及施工效率，可以采用二档工作速度进行碾压。

3.3 路面振动碾压参数及工艺组合分析

3.3.1 压路机重叠宽度分析

通过振动压实过程中路面应力分布规律的分析可以看出，虽然振动轮在横向上与路面之间接触宽度较大，但并非所有的接触区域均能够对路面沥青混合料进行有效的压实作用。因此在路面碾压施工时，会出现振动轮下方中间处的混合料压实效果好而边缘处的混合料压实效果较差。为了弥补这种沥青混合料横向压实不均匀的现象，压路机碾压过程中碾压轮迹需要有一定宽度的重叠，如图14。通过对比2种频率下的应力横向分布规律可以看出，2种频率下振动轮所产生的压实应力具有相同的横向分布规律。通过对2种频率下应力重叠曲线可以看出：67 Hz时压路机重叠宽度为0.6 m，而51 Hz时的重叠宽度则需要0.8 m，说明低频时过大的压实力会加剧振动轮两端力的发散效应而出现更为明显的横向碾压离析现象。综上所述，为了保障路面碾压过程中面层受力均匀性，在压路机往复碾压过程中要控制每次碾压时的轮迹与上一次碾压时的轮迹重叠宽度应该至少为轮宽的1/3左右，并适当根据压实参数进行相应的调整，以保证碾压均匀，提高压实结束后的路面平整度。

图14 压路机轮迹重叠示意图Fig.14 Schematic diagram of overlap of roller tracks

3.3.2 碾压参数组合分析

综合分析路面振动碾压过程中的应力及等效塑性应变在不同工况条件下的变化规律可以得出：“低频高幅高激振力”的压路机作业方式虽然可以明显提高路面面层沥青混合料的压实效果，但是通常由于需要压实的面层沥青混合料的厚度在10 cm左右，远薄于路面整体结构层厚，而且该工况下压路机会对整体路面结构造成较为强烈的冲击作用，导致混合料集料被振碎和过压等现象，从而影响路面使用性能。通过现场碾压过程中路面压实度变化规律可以知前3次压实对于路面沥青混合料的压实度贡献最大[19−20]。因此理论上，可以在沥青混合料阻尼较大的初压阶段采用该工作参数，同时采用较低的碾压速度，保证压实力的作用时间，迅速提高路面的压实度；而在复压时可采用高频低幅低激振力以及较快的碾压速度，以保证面层混合料级配的完整性以及施工效率。由于路面面层沥青混合料通常采用分层铺筑进行碾压，且路面下面层和中面层所用到的较大的最大公称粒径的沥青混合料，在压实过程中能够较快地达到目标压实度，同时较大的集料颗粒易受到压实力的作用而破碎，因此在施工时可以采用高频率振动状态和较慢的工作速度进行碾压，同时相应地减少压实次数，以平衡压实效果与施工效率。

基于以上分析，可以总结不同类型沥青混合料在压实施工过程中的压实工艺如表5所示。

表5 AC型沥青混合料碾压施工工艺组合Table 5 Combination of asphalt mixture rolling construction technology for AC pavement

4 结论

1)通过计算振动压实条件下路面结构及应力传递特征规律，发现在振动轮作用下的路面实际应力在横向分布上呈现出“两边小中间大”的特点，而碾压方向则可看作均匀分布。压路机振动荷载使路面结构内部产生压应力随着深度先以较快的速度衰减，随后缓慢衰减，最大作用深度可达2 m以上。

2)振动压路机不同的工作频率对应不同的激振力大小，从而影响到压路机振动轮作用于路面结构的压实应力。通过计算表明，压路机在低频率下路面沥青混合料的等效塑性应变相比高频下的混合料的等效塑性应变增加217%，压实应力及应力有效作用深度分别增加26%和95%。

3)压路机的工作速度同样影响压实效果。通过对比不同工作速度下路面沥青混合料的等效塑性应变发现，虽然不同档位速度下压路机作用于路面结构的压实力大小没有明显区别，但是采用较低速度下碾压可以使得路面沥青混合料获得更好的压实效果。

4)路面碾压过程中，需要制定详细的碾压阶段，并根据不同阶段选择碾压参数，上面层AC混合料在压实的初期阶段可采用“低频高幅”以及1档工作速度，保证路面面层能够获得足够的压实应力；而在后续压实过程中，可采用“高频低幅”和2档的碾压速度，压实过程中压路机之间的布置要合理，保证相邻碾压轨迹具有一定的重叠范围，避免压实不均。