如何正确运用方差分析——嵌套设计定量资料一元方差分析与SAS实现

胡纯严 ，胡良平 ，2*

（1.军事科学院研究生院，北京 100850；2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029*通信作者：胡良平，E-mail：lphu927@163.com）

多因素设计有很多种，它们之间的主要区别在于以下7个方面：①因素的性质、个数及水平数不尽相同；②全部因素的水平是否需要全面组合（每种组合被称为一个“试验点”）；③在各试验点上是否进行重复试验；④是否存在某些因素的水平是固定的，另一些因素的水平是随机选取的；⑤因素在施加时是否存在先后顺序之分；⑥从客观实际角度看，因素之间是否存在自然属性上的嵌套关系；⑦各因素对定量结果的影响是否存在主次之分。具备最后两点或其中之一的多因素设计类型被称为嵌套设计。嵌套设计是一种实用的多因素设计方法，本文将详细介绍该设计的主要特点、设计方法、定量资料一元方差分析的计算公式以及基于SAS软件实现定量资料方差分析的方法。

1 基本概念

1.1 嵌套设计

嵌套设计也被称为系统分组设计［1］。“嵌套”有两种含义：其一，因素之间存在包含关系或嵌套关系；其二，因素对定量结果的影响有主次之分［2］。嵌套设计就是依据实际问题中因素之间的相互关系或各因素对结果的影响情况，以谱系图的形式呈现出全部因素及其水平。例如，假定A、B、C这三个二水平因素之间存在包含关系，或者它们对结果的影响存在主次关系，可用结构图描述其关系。见图1。因素A（两个水平分别为A1和A2）为大组因素，因素B（两个水平分别为B1和B2）为中组因素，因素C（两个水平分别为C1和C2）为小组因素。

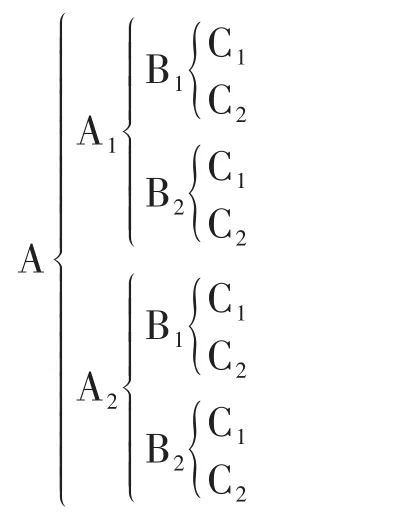
图1 3个二水平因素的嵌套设计结构图Figure 1 Nested design structure diagram of three two-level factors

1.2 嵌套设计的主要特点

由图1可知，嵌套设计近似一个2×2×2=23析因设计的架构［1-2］，但它们之间却存在诸多不同之处。嵌套设计的特点如下：①因素之间可能存在自然属性上的相互包含或嵌套关系，而不是相互独立的关系；或者受试对象具有分组再分组的条件，基于此，嵌套设计又称为系统分组设计［3］。②因素之间可能在对定量结果的影响上存在主次关系，而不是平等关系。③位于大组因素各水平之下的中组因素和小组因素的水平个数可以保持不变，但也可以变化；甚至水平的具体取值也可改变（参见后文表4），通常，中组或小组因素的水平是从众多水平中随机选取的［4-5］。④由于中组因素的每个水平并非都会出现在大组因素的每个水平之下，同样，小组因素的每个水平也并非都会出现在中组因素的每个水平之下，因此，在严格的嵌套设计中，各层级因素之间没有交互作用［4］。

1.3 误差的处理方法

针对嵌套设计的第二个和第三个特点，在对取自嵌套设计的定量资料进行方差分析时，分析大组因素时需采用中组因素的均方作为误差均方；分析中组因素时需采用小组因素的均方作为误差均方；分析小组因素时需采用模型误差均方作为误差均方。

2 嵌套设计定量资料一元方差分析的计算公式

假设有一个三因素嵌套设计一元定量资料，试验因素分别为A、B、C，其水平数分别为m、n、p。在每种试验条件下进行了r次独立重复试验，那么，总的受试对象数即为N=mnpr。三因素嵌套设计定量资料一元方差分析表见表1［4-5］。

表1 三因素嵌套设计一元定量资料的方差分析表Table 1 Analysis of variance table for the univariate quantitative data in three-factor nested design

表1中各统计量计算公式如下：

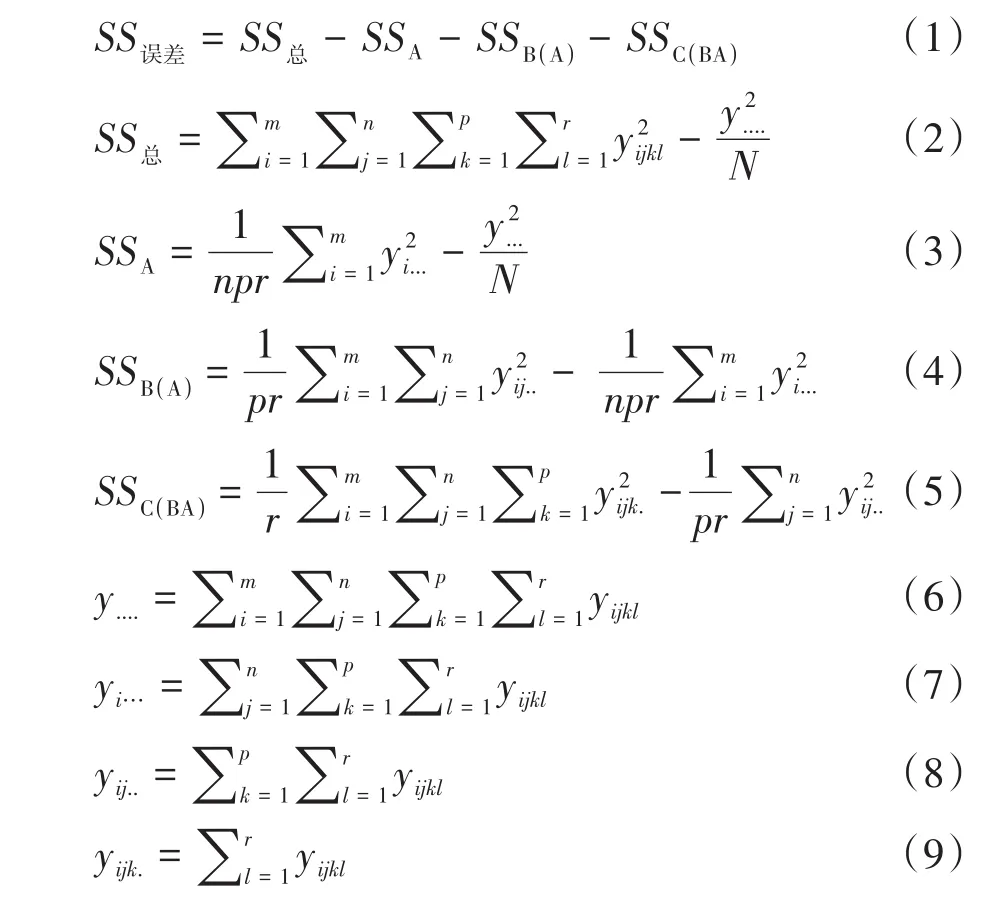
在以上各式中，i=1，2，…，m；j=1，2，…，n；k=1，2，…，p；l=1，2，…，r。

3 嵌套设计一元定量资料的实例与SAS实现

3.1 实例与数据结构

3.1.1 试验因素存在自然属性上的嵌套关系

【例1】为研究萝卜叶子中M物质的含量，随机采集3个萝卜（A1、A2、A3），在每个萝卜上随机取几片叶子（B1、B2、B3），萝卜叶子中M物质含量的测定结果见表2［2］。显然，M物质的含量，不仅取决于不同的叶子，更主要是与所取自的萝卜有关，即不同萝卜之间的变异大于同一个萝卜上的叶子之间的变异。试分析不同萝卜、不同叶片中的M物质含量的均值之间差异是否有统计学意义。

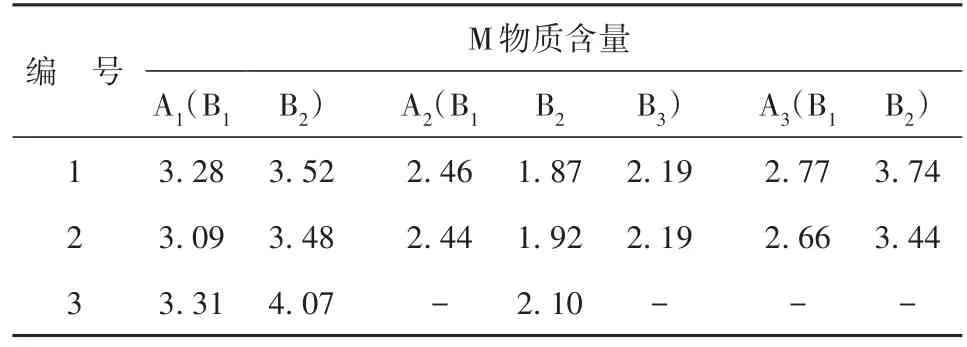
表2 萝卜叶子中M物质含量的测定结果Table 2 Measurement results of the substance M in the radish leaves

【例2】某公司拟分批次从3个供应商（S1、S2、S3）处购买某种原材料，已知该原材料的纯度在不同批次之间的变异很大，并可能影响产品质量。从每个供应商处随机分别抽取四批原材料，并在每批原材料中分别抽取三件测定其纯度。设计格式和资料见表3［4］。表3中的数据Y是“纯度值-93”的结果，目的是简化手工计算的复杂程度。试分析不同供应商、不同批次所对应的原材料纯度均值之间差异是否有统计学意义。

表3 原材料纯度的测量结果（Y=纯度值-93）Table 3 Measurement results of raw material purity（Y=purity value-93）

3.1.2 试验因素对定量结果的影响存在主次之分

【例3】某项化合物的试验研究涉及催化剂的种类和温度（℃）。依据专业知识，催化剂对该化合物转化率的影响大于温度的影响，且不同催化剂条件下所对应的温度不完全相同。设计格式和资料见表4［2］。试分析不同催化剂（其水平分别为甲、乙、丙）、不同温度（℃）（其水平分别为70、80、90；55、65、75；90、95、100）所对应的转化率均值之间的差别是否有统计学意义。

表4 某化合物在不同催化剂和不同温度下的转化率Table 4 Conversion rate of a compound under different catalysts and temperatures

3.1.3 嵌套设计与析因设计并存的设计

【例4】在印刷电路板上手动插入电子元件，以提高组装操作的速度。研究者设计了3种装配夹具（F1、F2、F3）和2个不同的工作场所（L1、L2）。从每个工作场所随机抽取4位操作者（O1、O2、O3、O4），他们对每个装配夹具重复操作两次。试验结果为装配时间（秒）。设计格式和资料见表5［4］。试分析3种夹具、2个工作场所、4位操作者所对应的装配时间均值之间差异是否有统计学意义。

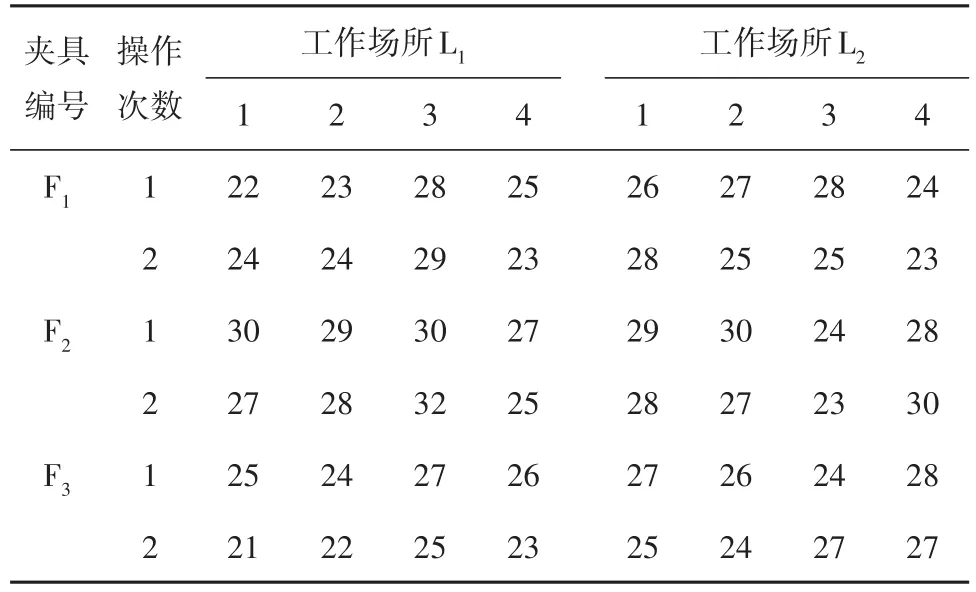
表5 不同操作者在不同工作场所装配夹具所用的时间Table 5 Time spent by different operators assembling fixtures in different workplaces

3.2 用SAS实现方差分析

3.2.1 对例1的分析与解答

【分析与解答】所需要的SAS程序如下：

【SAS程序说明】数据中的“.”代表缺失数据。

【SAS输出结果及解释】

由第一部分输出结果可知，不同叶片的M物质含量的均值之间差异有统计学意义（F=10.52，P=0.001 3）。

由第二部分输出结果可知，3个萝卜的叶子中M物质含量的均值之间差异有统计学意义（F=8.52，P=0.036 1）。值得注意的是，分析因素A（即大组因素）时，应采用因素B（即中组因素）的均方作为误差均方［6］。

【结论】不同萝卜的叶子中M物质含量差异有统计学意义，且同一个萝卜上不同叶片中的M物质含量差异也有统计学意义。

3.2.2 对例2的分析与解答

【分析与解答】所需要的SAS程序如下：

【SAS程序说明】第一个过程步调用GLM过程进行嵌套设计定量资料一元方差分析，需要用“TEST语句”为大组因素指定误差项［“b（s）”的含义是因素b嵌套在因素s之下］；而第三个过程步调用NESTED过程，只需将大组因素写在“class语句”中的第一位，将中组因素写在“class语句”中的第二位。

【SAS输出结果及解释】

由第一个过程步（GLM过程）的第1部分输出结果可知，4批原材料的纯度之间差异有统计学意义（F=2.94，P=0.016 7）。

由第一个过程步（GLM过程）的第2部分输出结果可知，3个供应商提供的原材料的纯度之间差异无统计学意义（F=0.97，P=0.415 8）。

由第三个过程步（NESTED过程步）输出结果可知，3个供应商提供的原材料的纯度之间差异无统计学意义（F=0.97，P=0.415 8），4批原材料的纯度之间差异有统计学意义（F=2.94，P=0.016 7）。

【说明】采用GLM过程计算时，需要通过“TEST语句”为大组因素和中组因素分别指定误差项，因此，解读输出结果时需谨慎；而采用NESTED过程计算时，可直接输出所需要的正确结果。

【结论】原材料的批次不同，产品纯度存在差异；但3个供应商提供的原材料的纯度比较接近。

3.2.3 对例3的分析与解答

【分析与解答】所需要的SAS程序如下：

【SAS程序说明】在以上SAS程序中，因素B的3个水平分别用1、2、3表示，而在表4中，因素B的水平值随着因素A的水平改变而改变。若严格按表4中因素的真实水平呈现，SAS程序如下：

后面的内容与前一段SAS程序相同，此处从略。

上面两段SAS程序输出结果完全相同。

【SAS输出结果及解释】

由第一部分输出结果可知，在不同温度条件下，化合物转化率的均值之间差异有统计学意义（F=12.15，P=0.000 7）。

由第二部分输出结果可知，在三种催化剂条件下，化合物转化率均值之间差异有统计学意义（F=14.63，P=0.004 9）。

【结论】化合物转化率均值会随着催化剂的改变而变化，也会随温度的改变而变化。具体地说，在甲催化剂条件下，转化率普遍较高，并且当温度居中（80℃）时，转化率最高；在乙催化剂条件下，转化率普遍较低，并且温度最高（75℃）时，转化率最低。

3.2.4 对例4的分析与解答

【分析与解答】所需要的SAS程序如下：

【SAS程序说明】“O（L）”的含义是因素O嵌套在因素L之下；第一个“TEST语句”的含义是用“F*O（L）”作为误差项分析“因素F”和“交互作用F*L”；第二个“TEST语句”的含义是用“O（L）”作为误差项分析“因素L”。

【SAS输出结果及解释】

由输出结果可知，操作者O（L）对试验结果的影响具有统计学意义（F=5.14，P=0.001 6）；交互作用F*O（L）对试验结果的影响具有统计学意义（F=2.35，P=0.030 0）；因素F（即夹具种类）对试验结果的影响具有统计学意义（F=7.55，P=0.007 6）；因素L（即工作场所）对试验结果的影响无统计学意义（F=0.34，P=0.580 7）。

【结论】3种夹具对应的试验结果均值之间差异有统计学意义，2个工作场所对应的试验结果均值之间差异无统计学意义，4位操作者对应的试验结果均值之间差异有统计学意义。

4 讨论与小结

4.1 讨论

对于嵌套设计而言，从因素分层角度来看，受试对象可以按多个因素进行逐层分组；从组间变异度角度来看，大组因素水平组之间的变异大于中组因素水平组之间的变异，中组因素水平组之间的变异大于小组因素水平组之间的变异。

嵌套设计中一个值得关注的情形是：位于中层或底层因素的水平个数以及水平的具体取值是可变的，有时是随机选取的。因此，嵌套设计定量资料的方差分析方法属于混合效应线性模型；若所有因素都是随机效应因素，则需要采用方差分量模型分析［4，6］。

4.2 小结

本文介绍了嵌套设计的基本概念和设计特点，总结出3类嵌套设计：试验因素存在自然属性上的嵌套关系、试验因素对定量结果的影响存在主次之分以及嵌套设计与析因设计并存的设计。基于4个实例，借助SAS软件实现了嵌套设计定量资料一元方差分析，并对SAS输出结果作出详细解读。