如何正确运用方差分析——分式析因设计定量资料一元方差分析与SAS实现

胡纯严 ，胡良平 ，2*

（1.军事科学院研究生院，北京 100850；2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029*通信作者：胡良平，E-mail：lphu927@163.com）

由于析因设计所需要的水平组合数很多，不可避免地增大了样本含量。当研究者对试验研究涉及的众多因素的情况了解甚少时，即使选用正交设计，其所需要的样本含量仍然较多。此时，可考虑选用分式析因设计。本文将介绍分式析因设计相关的基本概念、具体实施方法以及采用SAS实现定量资料方差分析和回归分析的方法。

1 基本概念

1.1 分式析因设计

将一个标准的析因设计按某种规则拆分成几部分，其中，每一部分称为原先析因设计的一个分式析因设计或分数析因设计［1-2］。

1.2 分式析因设计的意义

在一个多因素试验研究中，若高阶交互作用效应不存在或可以忽略不计，采用分式析因设计可以大幅度减少因素的水平组合数，即所需的样本含量更少。那么，减少的样本含量多少取决于研究者对试验结果精确度的要求。若对精确度要求较高，所需要的样本含量就相对较大。

1.3 分式析因设计中效应的混杂

由于分式析因设计可在较大幅度地减少因素水平组合数的前提条件下，尽可能容纳较多的因素，这就不可避免地导致某些因素或交互作用项的效应出现混杂。所谓“效应混杂”，就是某些效应项重叠在一起，例如，在设计表上，当交互作用AB与CD出现在同一列上时，从该列上计算出来不同水平之间的离均差平方和，就分不清它们各自的数量分别是多少。

1.4 混杂程度的分级

分式析因设计中的混杂情况有三类：分解Ⅲ设计、分解Ⅳ设计和分解Ⅴ设计［1，3］。

分解Ⅲ设计精确度最低，所需样本含量较少。在此类设计中，主效应彼此之间没有混杂，但主效应与两因素交互作用效应混杂，且两因素交互作用效应相互混杂。二水平因素的分解Ⅲ设计有很多种，例如

分解Ⅳ设计精确度居中，所需样本含量居中。在此类设计中，主效应彼此之间没有混杂，主效应与两因素交互作用效应之间没有混杂，但两因素交互作用效应彼此之间存在混杂，例如设计和设计。二水平因素的分解Ⅳ设计还有如下几种：设计［3］。

分解Ⅴ设计精确度最高，所需样本含量较多。在此类设计中，主效应或两因素交互作用效应与其他主效应或两因素交互作用效应之间没有混杂，但两因素交互作用效应与三因素交互作用效应存在混杂，例如设计。二水平因素的分解Ⅴ设计还有设计［3］。

分解Ⅴ设计以上的设计，其精确度更高，但所需要的水平组合数也更多，例如设计（即分解Ⅵ设计，水平组合数为32）和设计（即分解Ⅶ设计，水平组合数为64）。

以上是二水平因素的分式析因设计，此外，还有三水平因素和混合水平因素的分式析因设计［3-4］。因篇幅所限，此处从略。

2 分式析因设计定量资料方差分析的基本思想

根据试验因素的数目、水平数以及对计算结果精确度的要求，分式析因设计的种类非常多；由于不同的分式析因设计在设计表各列上出现的混杂情况不同，因此，不可能采用一个统一的方差分析公式解决所有分式析因设计定量资料的分析问题。

方差分析的基本思想：针对每个特定的分式析因设计，在接受其基本假设（例如，某些高阶交互作用效应不存在或可以忽略不计）成立的前提条件下，首先查看设计表中是否有空列，若有空列，则可用于估计第一类试验误差，也就具备进行方差分析的基本条件；其次，查看设计表的各行上是否进行了2次及以上独立重复试验，若已进行，则可用于估计第二类试验误差；第三，应明确设计表各列上估计的效应是否混杂。

若两类试验误差都无法估计，就不能进行方差分析；出现混杂的列上得出的计算结果是不正确的，因为它不是该列所代表的因素的效应或某个交互作用项的效应的真实值，而是混杂在一起的多个项的综合效应。

一般来说，若从设计表中无法直接估计试验误差，可先计算各列不同水平对应结果的平均值，采用最大值减去最小值求出极差。将设计表中极差最小的一列或多列视为“空白列”（因为它们的效应很小，对试验结果的影响微乎其微），它们将被用于估计第一类试验误差。

3 分式析因设计一元定量资料的方差分析与SAS实现

3.1 实例与数据结构

【例1】某化学试验涉及4个二水平因素：温度（A）、压力（B）、甲醛的浓度（C）和搅拌速度（D）。若采用24析因设计，因素的水平组合数为16，拟采用设计，即进行24析因设计的二分之一实施。试验安排与结果见表1［3］。试分析4个因素对过滤率的影响是否有统计学意义。

表1 4个二水平因素的试验设计及结果Table 1 Design and the experimental results of four two-level factors

【例2】一项关于润滑油质量的试验，涉及4个三水平因素：A、B、C和D（它们的专业含义从略）。各因素均取相同间隔的水平1、2、3。由于这是一个预试验，拟采用-34设计，即34-1设计，实际上就是4个三水平因素析因设计的三分之一实施。试验安排与结果见表2［4］。试分析4个因素对定量试验结果的影响是否有统计学意义，并分别分析因素的线性部分和二次项部分是否有统计学意义。

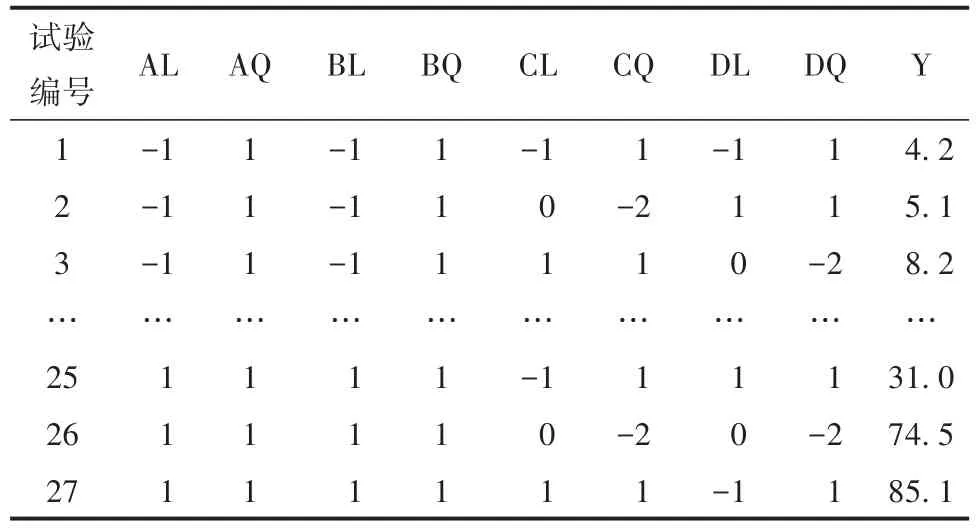
表2 4个三水平因素析因设计的三分之一实施及试验结果Table 2 One-third implementation and the experimental results of four three-level factorial designs

3.2 用SAS实现方差分析

3.2.1 对例1的分析与解答

【分析与解答】所需要的SAS程序如下：

【SAS程序说明】第一个和第二个过程步（PROC UNIVARIATE和PROC PRINT）用于计算各列因素的两个水平下过滤率平均值之差量（简称为“效应”）；第三个过程步（PROC GLM）用于进行方差分析［5］；第四个过程步（PROC REG）用于进行多重线性回归分析［5］。

【SAS输出结果及解释】

以上是各列的效应输出结果，其中，第2～5列对应4个因素各自的效应，后3列对应3个两因素之间的交互作用的效应。因素B的效应和交互作用AB的效应很小，故可以将它们合并到误差项中去。

由第三个过程步输出的结果可知，因素x1（A）、因素x3（C）、因素x4（D）、交互作用x1*x3和交互作用x1*x4这5项对过滤率的影响均有统计学意义，与它们对应的检验统计量F值和P值如下。x1：F=222.15，P=0.004 5；x3：F=120.62，P=0.008 2；x4：F=167.54，P=0.005 9；x1*x3：F=210.62，P=0.004 7；x1*x4：F=222.15，P=0.004 5。

由第四个过程步输出的结果可知，多重线性回归模型中的各项均有统计学意义。基于回归系数的计算结果，可写出多重线性回归模型：

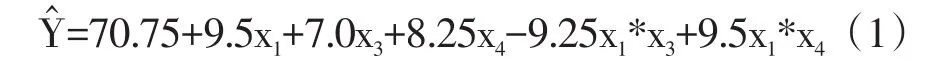
基于上述多重线性回归方程，可以对过滤率进行预测。例如，当3个因素都取1水平时，则有：

文献［3］给出了与此例对应的完全析因设计（24析因设计）资料及回归方程如下：

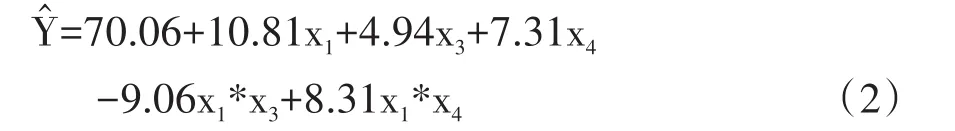
基于上述多重线性回归方程，可以对过滤率进行预测。例如，当3个因素都取1水平时，则有：Ŷ=70.06+10.81+4.94+7.31-9.06+8.31=92.37（%）。

由此可知，采用24析因设计的二分之一的设计（即24-1设计），可以获得与原设计（指24析因设计）十分近似的统计分析结果和结论。

3.2.2 对例2的分析与解答

【分析与解答】所需要的SAS程序如下：

【SAS输出结果及解释】

由第一个过程步定义的总模型的方差分析输出结果可知，总模型有统计学意义（F=11.87，P<0.000 1）。

由第一个过程步定义的总模型中各因素的方差分析输出结果可知，因素A（F=16.34，P<0.000 1）、因素B（F=10.06，P=0.001 2）和因素C（F=20.06，P<0.000 1）对定量结果的影响均有统计学意义，而因素D（F=1.03，P=0.377 2）则无统计学意义。

由第二个过程步的输出结果可知，就4个因素对结果影响的线性部分（分别为AL、BL、CL和DL）的方差分析结果而言，因素A（F=31.98，P<0.000 1）、因素B（F=20.06，P<0.000 1）和因素 C（F=40.09，P<0.000 1）的线性部分均有统计学意义，因素D（F=1.55，P=0.228 8）的线性部分无统计学意义。

由第三个过程步的输出结果可知，4个因素对定量结果影响的二次方部分（分别为AQ、BQ、CQ和DQ）的方差分析结果均无统计学意义（具体的F值和P值从略）。

由第四个过程步的输出结果可知，因素B（即x2）（F=21.11，P=0.000 1）、因素 C（即 x3）（F=43.98，P<0.000 1）和因素A的平方项（即x12）（F=35.85，P<0.000 1）对结果的影响均有统计学意义。对应的多重线性回归方程如下：

4 讨论与小结

4.1 讨论

与相同规模的析因设计相比，一个特定的分式析因设计可安排的因素个数相同，但因素的水平组合数更少。对于二水平因素而言，通常可以减少二分之一或四分之三或八分之七；对于三水平因素而言，通常可以减少三分之一或九分之八或二十七分之二十六。然而，其结果的精确度会降低：减少的组合数越多，精确度越低。一系列分式析因设计的表格见文献［3，6］。

4.2 小结

本文介绍了分式析因设计的基本概念以及二水平因素和三水平因素的分式析因设计的具体实施，基于SAS软件实现了二分之一24析因设计和三分之一34析因设计定量资料一元方差分析，并对定量资料进行多重线性回归分析，给出了可用于预测的多重线性回归方程。