如何正确运用方差分析——正交设计定量资料一元方差分析与SAS实现

胡纯严 ，胡良平 ，2*

（1.军事科学院研究生院，北京 100850；2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029*通信作者：胡良平，E-mail：lphu927@163.com）

正交设计是安排多因素的一种高效方法，在满足某些特定条件时，正确地运用正交设计，不仅可以获得比较精准的试验结果，而且所需的样本含量较少。本文将介绍正交设计的基本概念、设计方法、计算公式以及基于SAS软件实现正交设计定量资料方差分析的方法。

1 基本概念

1.1 正交

在几何学上，正交的意思是两条直线互相垂直。在代数学上，若两个向量的内积（或称数量积）等于0，就定义这两个向量是互相正交的［1］。假设有两个向量如下：a=（-1，-1，-1，-1，1，1，1，1），b=（-1，1，-1，1，-1，1，-1，1）。将它们对应位置上的数字相乘后求和，可记为（a，b）=-1×（-1）+（-1）×1+……+1×1=0，它就是向量a与向量b的“内积”。于是，在数学上，称上面两串数字排成的序列或向量是互相正交的。

在统计学上，统计学家构造出一系列类似于上面给出的“向量”，将它们排列在一张表格中，表格中任何两列数据的“内积”都等于0，这种表格就叫做正交表［2］。以L8（27）正交表为例，其中“L”代表正交表，数字“8”代表此表有8行，数字“2”代表每列有2个不同的水平，数字“7”代表此表有7列。L8（27）正交表见表1。表1共有7列，每列可以代表一个试验因素的2个水平各重复出现4次的一种排列；实际使用时，每列可以安排一个二水平因素，每行代表全部因素的一种水平组合结果，例如，第1行所有因素都取“1水平”。若用“-1”取代表中的“2”，则表1中的任何两列的“内积”都等于0。

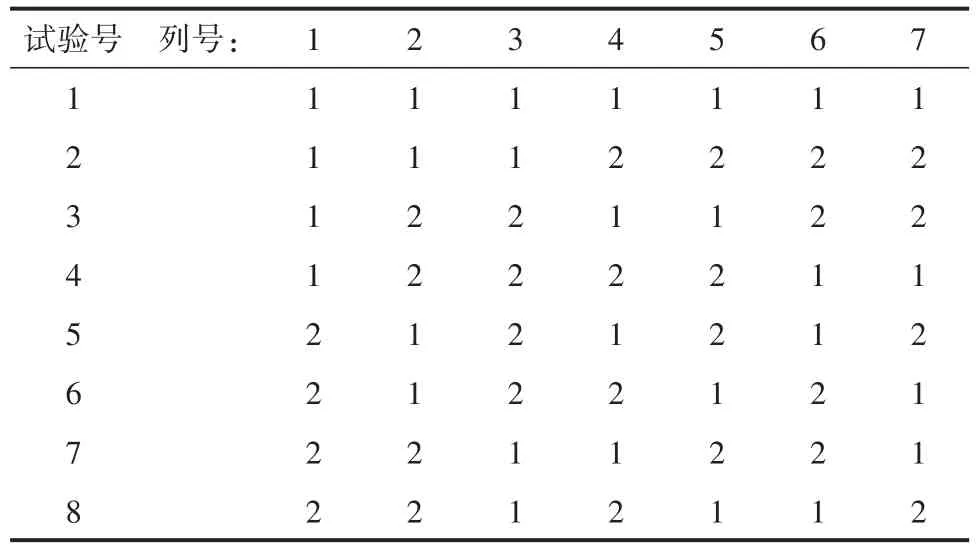
表1 L8（27）正交表Table 1L8（27）Orthogonal table

1.2 正交设计

正交设计是利用一系列规格化的正交表来安排各试验因素及其水平组合的方法。正交表是经过严格的数学推导编制而成，正交表中的每一行代表全部试验因素的一种水平组合，称为一个试验点；正交表中的每一列代表一个试验因素（或交互作用项）及其水平的排列和重复出现的情况，将全部因素及其拟考察的交互作用项恰当地安排在正交表的表头上，就叫做正交设计。

1.3 正交设计的特点

正交设计有4个突出特点：①由正交表挑选出来的试验点在空间上具有“均匀分散性”；②由正交表挑选出来的试验点在统计分析时具有“整齐可比性”；③某些未包括在正交表中的试验点，可以通过统计分析将其发现；④在某些假设（例如某些因素之间的交互作用不存在或可以忽略不计，特定试验条件下试验结果的稳定性很好）成立的条件下，正交设计比其他多因素设计（排除均匀设计）所需的样本含量更少。

1.4 正交设计误差处理

在采用正交设计安排试验时，应预先考虑好如何估计试验误差：在正交表中留有空白列（可用于估计不同试验条件之间所产生的试验误差，被称为第一类误差），或者在挑选出来的试验点上进行m次独立重复试验（m≥2，可用于估计相同试验条件下不同重复试验次数之间所产生的试验误差，被称为第二类误差）。一般来说，第一类误差大于第二类误差。在对资料进行方差分析时，若只有第一类误差，就以其均方为分母，构造F检验统计量；若有两类误差，就需要将它们的离均差平方和、自由度分别进行合并，用合并后的离均差平方和除以合并后的自由度，构造出误差的均方。误差项的自由度越大（意味着所需要的样本含量越大），所得结论的可信度就越高。

1.5 正交表的种类

正交表可分为两大类：第一类是饱和正交表，第二类是非饱和正交表，也称不完备正交表［3］。在不做重复试验的饱和正交表中，总自由度=各列自由度之和=表的行数－1，各列自由度=各列中不同水平数－1。总自由度不等于各列自由度之和的正交表，就是非饱和正交表。例如，在L8（27）正交表中，df总=8－1=7，每一列的自由度=2－1=1，7列自由度之和=7，满足“总自由度=各列自由度之和”的要求，故L8（27）正交表是饱和正交表。

根据正交表中各列的水平数是否相等，还可将正交表分为同水平正交表与混合水平正交表［4-5］。常见的同水平正交表有：二水平的正交表［L4（23）、L8（27）、L16（215）、L32（231）、L64（263）］，三水平的正交表［L9（34）、L27（313）、L81（340）］，四水平的正交表［L16（45）、L64（421）］，五水平的正交表［L25（56）、L125（531）］。常见混合水平的正交表有：L8（4×24）、L12（3×24）、L16（42×29）、L16（43×26）、L18（2×37）、L18（6×36）、L27（9×39）、L32（45×216）、L36（6×312）、L32（16×216）、L24（3×4×24）、L36（62×35×2）、L32（8×46×26）。

有些混合水平正交表是非饱和正交表，例如，在L12（3×24）正交表中，总自由度=12－1=11，而各列自由度之和=（3－1）+4×（2－1）=6。

2 正交设计定量资料一元方差分析的计算公式

正交表的种类很多，且因素的个数、水平数以及需要考察的交互作用项数都会随着具体问题发生变化，还涉及是否进行重复试验。因此，无法给出一个统一的正交设计定量资料一元方差分析计算公式。现假定在L8（4×24）的前3列上分别安排因素A（4水平）、因素B（2水平）和因素C（2水平），扼要介绍正交设计定量资料一元方差分析的计算思路。计算正交表中每一列上的离均差平方和的方法，与单因素两水平或多水平设计定量资料一元方差分析计算组间离均差平方和的方法相同，可参见文献［6］。

第一步，计算最后一列试验结果Y的总离均差平方和。

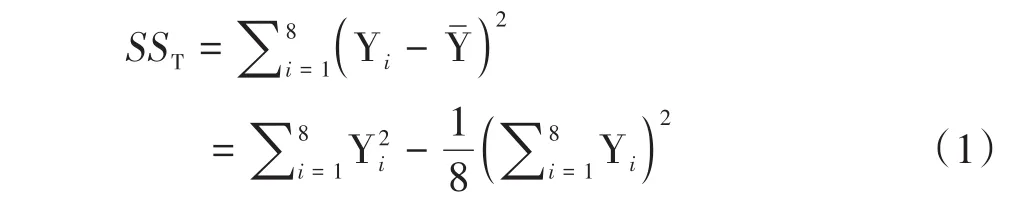
第二步，计算A、B、C列试验结果Y的总离均差平方和。

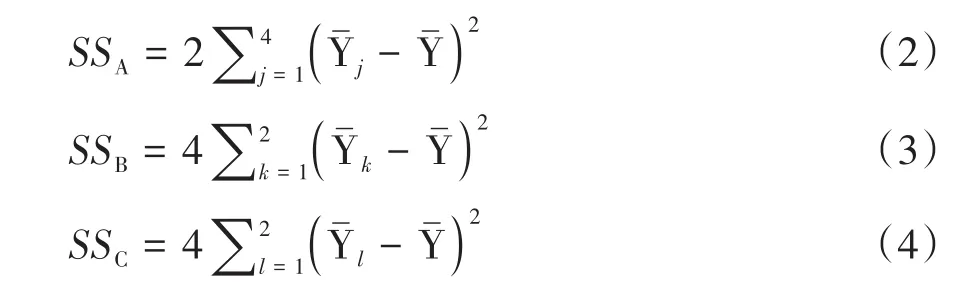
第三步，计算误差E的离均差平方和。

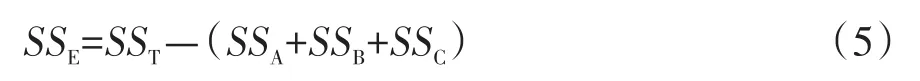
第四步，计算总自由度和因素A、B、C的自由度以及误差E的自由度。

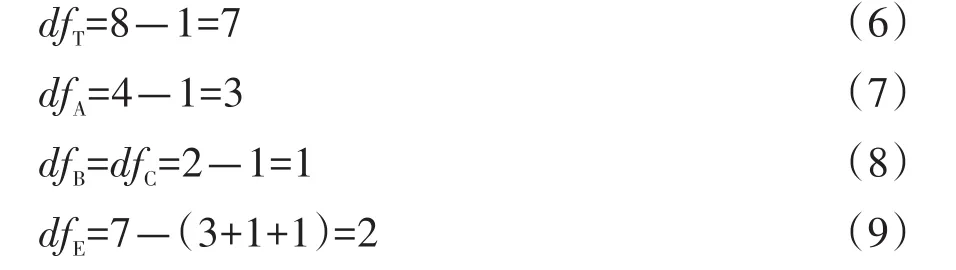
第五步，计算误差的均方和因素A、B、C的均方。

第六步，计算与因素A、B、C对应的检验统计量F的值。

若基于手工计算，需根据计算检验统计量F值的分子和分母的自由度去查方差分析用的F临界值表，再比较检验统计量F值与其对应的F临界值的大小，做出统计推断。因篇幅所限，此处从略。本文将基于SAS软件实现方差分析［7］。

3 正交设计定量资料一元方差分析的实例与SAS实现

3.1 实例与数据结构

【例1】某化工厂为了提高产品的收率，根据具体情况和经验确定试验条件如下：因素A为反应温度（A1=30℃，A2=40℃）；因素B为反应时间（B1=60 min，B2=90 min）；因素C为两种原料比（C1=1∶1，C2=1.5∶1）；因素D为搅拌速度（D1=慢，D2=快）。选用L8（27）正交表安排上述4个因素，试验结果见表2［4］。试分析哪些因素对收率Y的影响有统计学意义。

表2 4个试验因素对产品收率影响的试验结果Table 2 Experimental results of the influence of four experimental factors on the product yield

【例2】某电解腐蚀试验考察4个三水平因素（各因素的具体含义从略），交互作用均不考虑。试验指标为产品质量，按照规定标准进行综合评分。选用L9（34）正交表安排试验，在每个试验条件下进行3次重复试验。试验安排和试验结果见表3［3］。试分析4个因素对试验结果的影响是否有统计学意义。

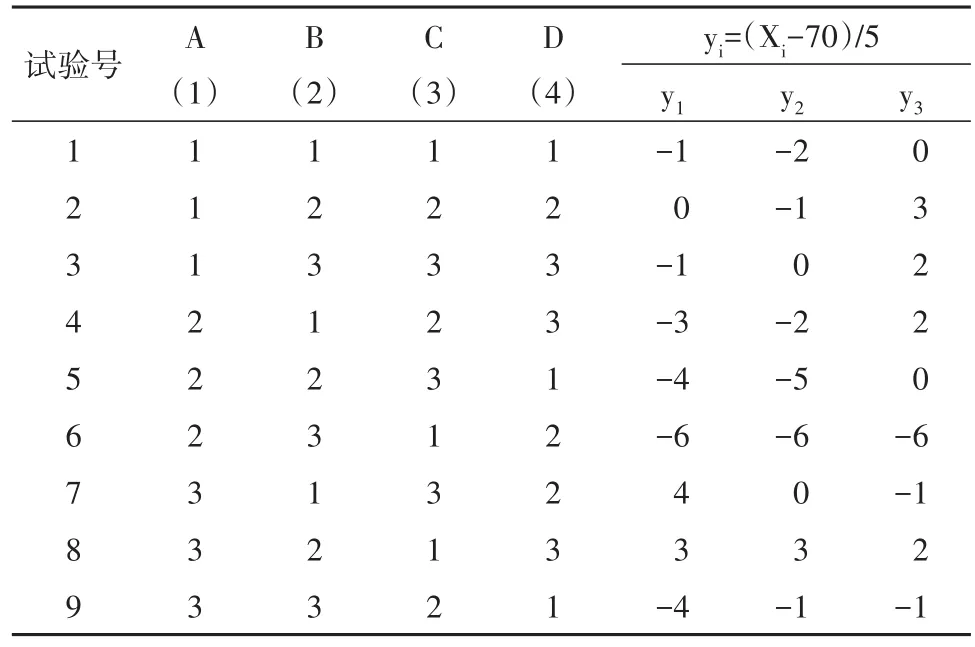
表3 4个三水平因素对电解腐蚀作用的正交设计及试验结果Table 3 Orthogonal design and the experimental results of four three-level factors on the role of the electrolytic corrosion

【例3】某农业科研所为了提高小麦产量，拟考察A、B、C三个因素对小麦亩产的影响。各因素各水平的含义如下：因素A为品种，有4个水平，1～4分别代表泰山4号、济6矮、矮秆早、139号；因素B为施肥量，有2个水平，1和2分别代表高肥和低肥；因素C为播种期，有2个水平，1和2分别代表早播和晚播。试验安排和试验结果见表4［5］。试分析三个因素对小麦亩产Y的影响是否有统计学意义？

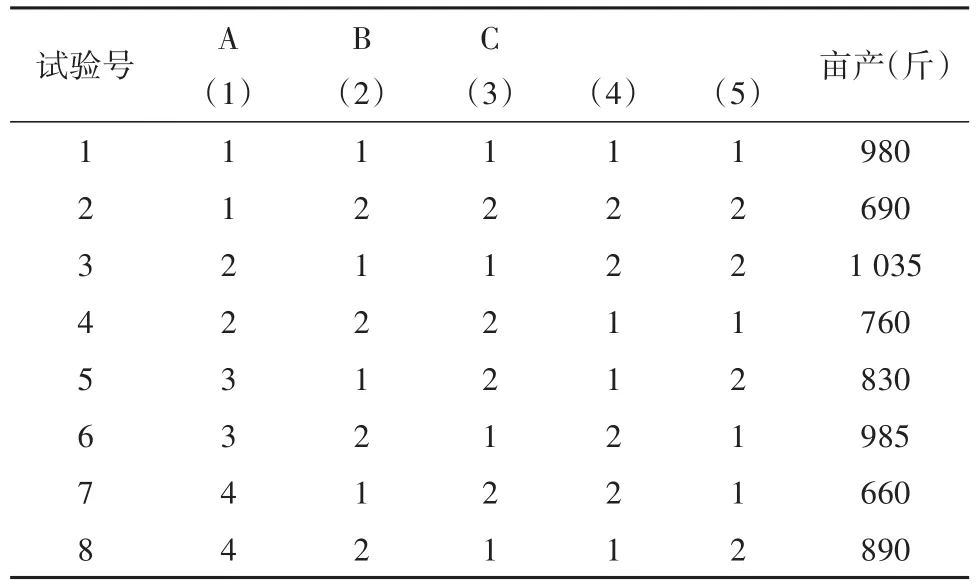
表4 3个因素对小麦亩产影响的正交设计及试验结果Table 4 Orthogonal design and the experimental results of the influence of three factors on the wheat yield per mu

3.2 用SAS实现方差分析

3.2.1 对例1的分析与解答

【分析与解答】所需要的SAS程序如下：

【SAS程序说明】在SAS过程步中，有四个“model语句”，第一个是可执行的，后三个放在注释语句“/**/”中是不可执行的。每次运行SAS程序，只能让一个“model语句”处于可执行状态。

【SAS输出结果及解释】

由第一个“model语句”的输出结果可知，4个因素均无统计学意义，其中，因素D的作用最小。因篇幅所限，具体输出结果从略，下同。

由第二个“model语句”的输出结果可知，因素C（F=11.54，P=0.042 6）和交互作用项A*B（F=11.54，P=0.04 26）具有统计学意义，而因素A（F=2.88，P=0.188 0）和因素B（F=2.88，P=0.188 0）均无统计学意义。

由第三个“model语句”的输出结果可知，因素C（F=11.54，P=0.042 6）具有统计学意义，而交互作用项A*B（F=5.77，P=0.092 0）无统计学意义。

由第四个“model语句”的输出结果可知，当模型中仅有因素C时，它对定量观测结果的影响变得无统计学意义（F=3.41，P=0.114 4）。

由以上分析过程和结果可知：多因素方差分析结果是相对的，不是一成不变的。因为随着模型中待分析的项的改变（在本质上，是模型误差的均方在改变），各因素及交互作用项的统计显著性也会发生变化。

3.2.2 对例2的分析与解答

【分析与解答】所需要的SAS程序如下：

【SAS输出结果及解释】

由第一个过程步的输出结果可知，因素C（F=0.54，P=0.591 0）对试验结果的影响无统计学意义，因素A（F=11.20，P=0.000 7）、因素B（F=5.17，P=0.016 9）、因素D（F=5.01，P=0.018 6）对试验结果的影响均有统计学意义。因篇幅所限，具体输出结果从略，下同。

由第二个过程步的输出结果可知，因素A（F=11.74，P=0.000 4）、因素B（F=5.41，P=0.013 2）、因素D（F=5.25，P=0.014 7）对试验结果的影响均有统计学意义。

因为结果的平均值越大越好（为节省篇幅，4个因素各水平下的均值计算结果从略），故因素A应取第三个水平，因素B应取第二个水平，因素C应取第三个水平，因素D应取第三个水平。

3.2.3 对例3的分析与解答

【分析与解答】所需要的SAS程序如下：

【SAS程序说明】在SAS过程步中，有三个“model语句”，第一个是可执行的，后两个放在注释语句“/**/”中是不可执行的。每次运行SAS程序，只能让一个“model语句”处在可执行状态。

【SAS输出结果及解释】

由第一个过程步的输出结果可知，仅因素C（F=154.27，P=0.006 4）对产量的影响具有统计学意义。

由第二个过程步的输出结果可知，在淘汰掉P值最大的因素B之后，仍然只有因素C（F=61.39，P=0.004 3）对产量的影响具有统计学意义。

由第三个过程步的输出结果可知，在淘汰掉因素A和因素B之后，因素C（F=23.98，P=0.002 7）对产量的影响仍有统计学意义。

4 讨论与小结

4.1 讨论

标准正交表对因素的水平数有严格要求，但在某些实际问题中，很难完全与之符合，此时，就需要对原先的正交表进行改造。例如，多个因素有3个水平，少数因素有2个水平，又没有相应的混合水平正交表可以使用。此时，可采用“拟水平法”将二水平因素改造成三水平因素［5］。在有的试验中，根据研究者经验，在安排方案时已知某些因素之间存在依赖关系，一个因素用量或水平的选取需要随另一个因素用量或水平而定，这时就需要采用“活动水平法”［5］；在有的试验中，按正交表做了一些试验后，用趋势图分析发现某一因素对试验指标的影响存在某种变化趋势，研究者认为有必要对该因素添加新的水平并追加几次试验，以便对它的影响有更全面的了解，此时，就需要采用“部分追加法”［5］。

值得注意的是，对标准正交表进行改动后，对定量资料进行方差分析的方法也需相应改变，否则，会影响计算结果的精确度；当正交表中的评价指标或结果变量有多个时，若它们之间存在一定的关联，就需要同时对它们进行分析。常规的统计分析方法是正交设计定量资料多元方差分析［8］，还有一种统计分析方法是“广义方差分析”［5］。因篇幅所限，本文不予赘述。

4.2 小结

本文介绍了正交设计的基本概念、具体实施方法以及定量资料一元方差分析的计算公式，通过三个实例，展示了二水平、三水平和混合水平正交设计的具体实施方法；还给出了无重复试验和有重复试验定量资料方差分析的SAS实现方法。