如何正确运用方差分析——析因设计定量资料一元方差分析与SAS实现

胡纯严 ，胡良平 ，2*

（1.军事科学院研究生院，北京 100850；2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029*通信作者：胡良平，E-mail：lphu927@163.com）

析因设计是一种全因素试验设计方法，也就是要在全部试验因素的各种水平组合条件下进行2次及以上独立重复试验。通过此设计收集到的定量资料，可以全面反映所有试验因素及其各阶交互作用项对定量观测结果影响的详细信息。本文将介绍析因设计的特点、具体实施方法、定量资料一元方差分析的计算公式和SAS实现方法。

1 基本概念

1.1 析因设计

析因设计是安排因素之间存在复杂交互作用的多因素试验的重要方法［1-2］。具体做法如下：罗列出试验因素的全部水平组合，在每种组合（称为试验点）条件下，进行2次及以上独立重复试验。

1.2 析因设计的特点

析因设计具有以下7个特点［2］：①试验因素的个数≥2；②每个试验因素的水平数≥2，且各因素的水平数可以不等；③不同的试验条件数（或组合数或试验点数）等于全部试验因素的水平数之乘积；④各试验条件下至少进行2次独立重复试验；⑤全部受试对象被完全随机地分配进入任何一个试验条件组中，各小组中的受试对象个数相等为最佳，但也可以不等；⑥试验时，每次试验都涉及任一试验因素的某个水平，即全部试验因素同时施加；⑦进行统计分析时，假定全部试验因素对观测结果的影响是平等的，即没有主次之分。由此可知，析因设计的明显优点是可以分析每个试验因素的主效应以及试验因素之间各阶交互作用的效应大小；缺点在于总试验次数太多，费时费力且增加试验费用。

1.3 交互作用

析因设计是考察因素之间各阶交互作用效应的主要方法。高阶交互作用效应的解释是非常困难的，现以最常见的一阶交互作用（即两因素之间的交互作用）为例，解释其含义［3］。

假设在某项药物试验研究中，需要将A药与B药联合使用，若在固定的剂量下，两药联合使用比单用任何一种药物的疗效更好，则称这两种药物具有协同作用；反之，则称这两种药物具有拮抗作用。协同作用和拮抗作用都不是交互作用。A药与B药之间具有交互作用是指当A药分别取不同剂量时，其疗效的差别并非一成不变，而是会随着与之联用的B药剂量的改变而改变。例如，当B药取低剂量时，A药取高剂量的疗效优于A药低剂量的疗效；而当B药取高剂量时，A药取低剂量的疗效优于A药高剂量的疗效。在统计学上，A药的剂量与B药的剂量之间存在交互作用效应。至于交互作用效应是否有统计学意义，则需要通过假设检验来做出统计推断，还需要通过大样本临床试验进一步验证。

1.4 析因设计的架构

析因设计将二维平面划分成多行与多列的网状结构，其网格数就是全部试验因素的水平组合数。在此网状结构中，行数可代表一个试验因素的全部水平数或若干个试验因素的水平组合数，列数可代表一个试验因素的全部水平数或若干个试验因素的水平组合数。因篇幅所限，析因设计的具体架构见后文各表格，此处从略。

2 析因设计定量资料一元方差分析的计算公式

由于析因设计常用于安排有2～4个试验因素（因为因素过多时，各水平组合条件下仍需要做重复试验，故总试验次数很多，实际科研工作者一般难以承受）的试验研究场合，因此，其方差分析计算公式至少有三种。然而，随着因素个数的增加，因素之间的各阶交互作用项数也相应增加：当有A和B两个因素时，只有一个交互作用项（AB）；当有A、B、C三个因素时，有4个交互作用项（AB、AC、BC、ABC）；当有A、B、C、D四个因素时，就有11个交互作用项（AB、AC、AD、BC、BD、CD、ABC、ABD、ACD、BCD、ABCD）。因篇幅所限，本文仅呈现两因素析因设计定量资料一元方差分析的计算公式，其他情况下的计算公式从略。

现以两因素析因设计定量资料为例，介绍其总离均差平方和（简称“总变异”）的分解方法［1，4］。设试验因素A有a个水平，试验因素B有b个水平，在因素A和因素B各水平组合条件下进行r次独立重复试验，则受试对象总数（即总样本含量）N=abr，其方差分析表见表1。

表1 两因素析因设计定量资料方差分析表Table 1 Analysis of variance for the quantitative data with two-factor factorial design

表1中各统计量计算公式如下：

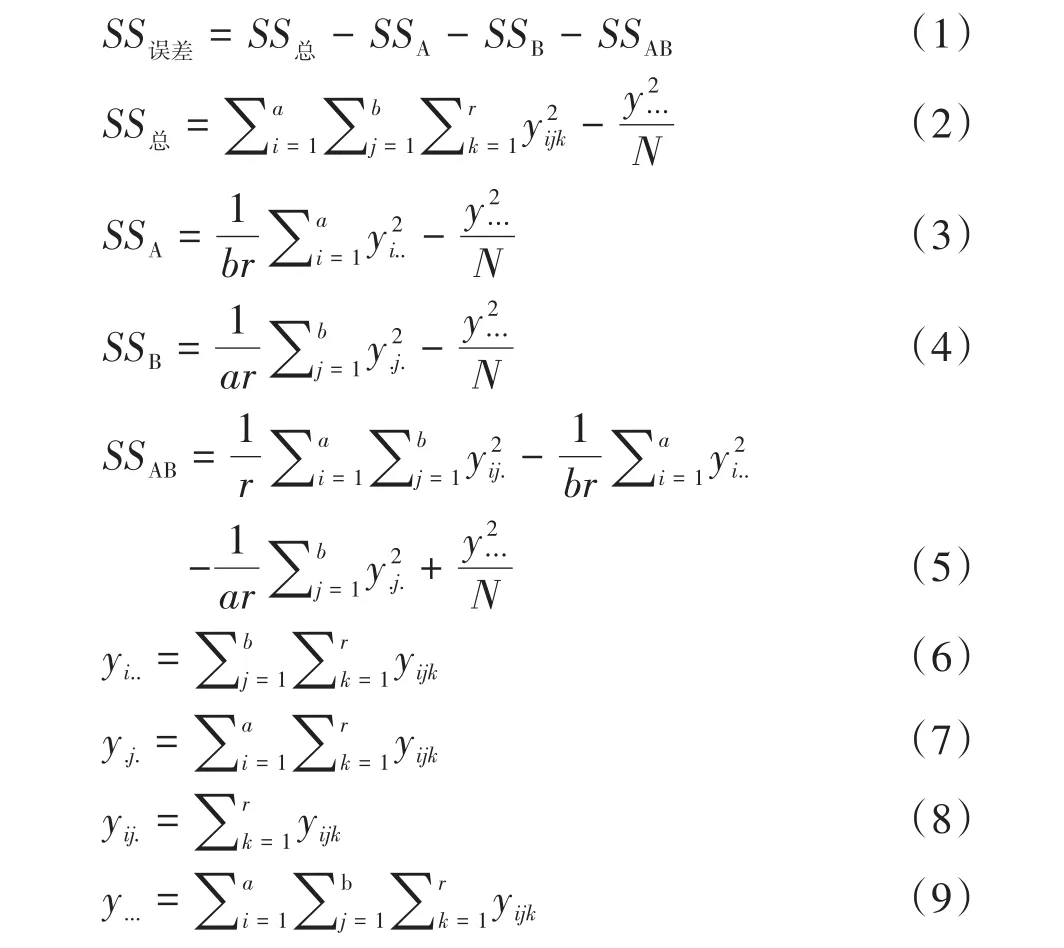
在以上各式中，i=1，2，…，a；j=1，2，…，b；k=1，2，…，r。

3 析因设计一元定量资料的实例与SAS实现

3.1 实例与数据结构

【例1】为了给一种装置设计出一种寿命长的电池，研究者根据经验确定了两个重要试验因素，一个是制造电池材料的种类（因素M），另一个是研究者设定的试验温度（因素T）。因素M取3个水平，1～3分别代表三种不同的材料；因素T取3个水平，1～3分别代表15℉、70℉和125℉。为了较好地估计试验误差，研究者拟在每种水平组合下进行4次独立重复试验。试验安排与试验结果见表2［1］。试分析各因素及其交互作用项对电池寿命的影响是否有统计学意义。

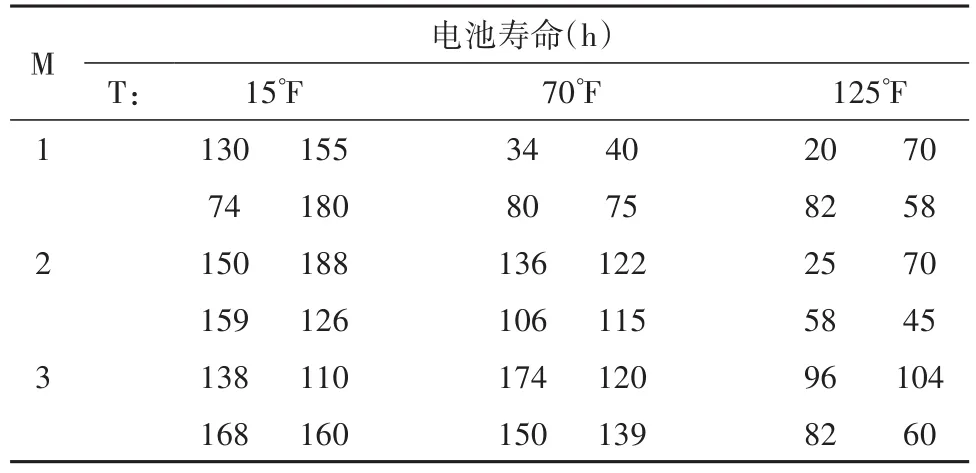
表2 材料种类（M）与试验温度（T）对电池寿命影响的试验结果Table 2 Experimental results of the influence of material type（M）and the experimental temperature（T）on battery life

【例2】某试验同时涉及A、B、C三个地位平等的试验因素，A有2个水平，B有3个水平，C有4个水平，观测指标为OD值，受试对象为样品，在不同试验条件下均独立地重复做了2个样品，资料见表3［2］。试分析两因素及其交互作用项对OD值的影响是否有统计学意义。

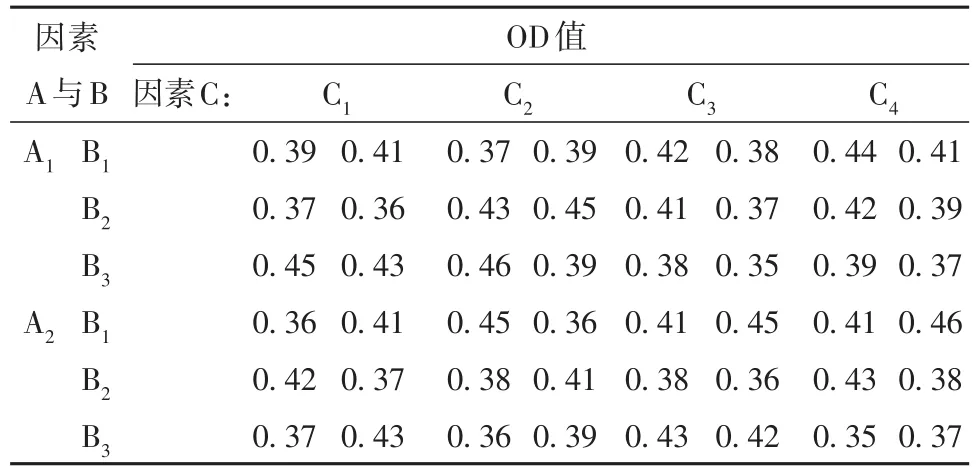
表3 3个试验因素作用下OD值的测量结果Table 3 Measurement results of OD value under the action of three experimental factors

3.2 用SAS实现方差分析

3.2.1 对例1的分析与解答

【分析与解答】所需要的SAS程序如下：

【SAS输出结果及解释】

由两因素析因设计定量资料一元方差分析总模型的检验结果可知，总模型具有统计学意义（F=11.00，P<0.000 1）。

由两因素及其交互作用项的输出结果可知，材料种类（M）（F=7.91，P=0.002 0）、试验温度（T）（F=28.97，P<0.000 1）及其交互作用项（M*T）（F=3.56，P=0.018 6）对电池寿命的影响均有统计学意义。

材料种类（M）与试验温度（T）之间的交互作用效应见图1。横轴为材料种类（M），分别取1、2、3水平；纵轴为试验结果电池寿命（Y，单位：h）。图中从上到下的三条折线对应的试验温度（T）分别为1、2、3水平。显然，T=1（即温度为15℉，低温）时，用三种材料制造的电池寿命普遍长；随着温度逐渐增加，用三种材料制造的电池寿命逐渐缩短。然而，图中的3条折线的变化趋势是不同的（显然，它们不是互相平行的），当M=1时，T=2与T=3两条折线相交；当M=3时，T=1与T=2两条折线相交。

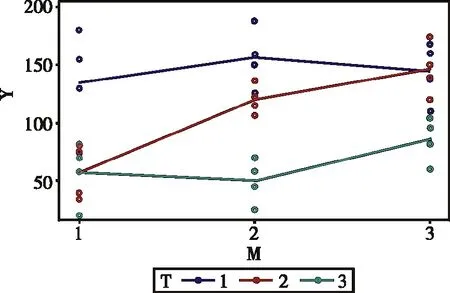
图1 材料种类（M）与试验温度（T）交互作用效应图Figure 1 Graph reflecting the interaction effect between the material type（M）and the experimental temperature（T）

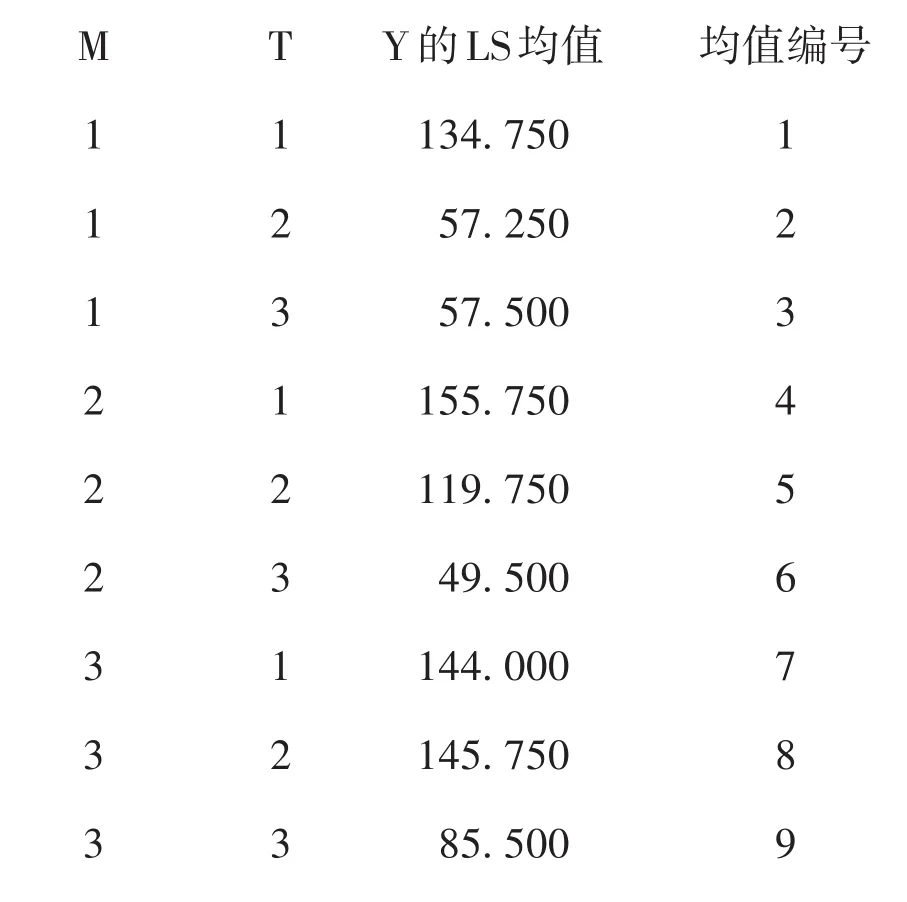
以上输出的是因素M（材料种类）与因素T（试验温度）在各种水平组合条件下，试验结果Y的平均值，并将这9种水平组合编号为1～9。编号1～3的均值代表M=1（即在第一种材料的前提条件下）的三种温度所对应的试验结果Y的平均值；编号4～6的均值代表M=2（即在第二种材料的前提条件下）的三种温度所对应的试验结果Y的平均值；编号7～9的均值代表M=3（即在第三种材料的前提条件下）的三种温度所对应的试验结果Y的平均值。同理，可理解编号（1、4、7）、（2、5、8）和（3、6、9）的均值含义，即在同种试验温度条件下，用三种材料制造的电池的平均寿命的均值。

采用TUKEY法对因素M与因素T的9种水平组合下的9个平均值进行两两比较。因篇幅所限，此部分结果从略。现将它们之间的比较结果解释如下。

在如此多的两两比较的结果中，研究者最关心的是将两个因素中的一个控制在特定水平上，考察另一个因素各水平组平均值差异是否有统计学意义。例如：在温度为第3个水平（即125℉）条件下，三种材料所对应的电池寿命的平均值差异是否有统计学意义？可查看编号为3、6、9的3个均值（57.500、49.500、85.500）之间对应的P值：编号3与编号6之间的P值为1.000 0，编号3与编号9之间的P值为0.834 7，编号6与编号9之间的P值为0.581 9。三个P值均大于0.05，说明当温度高（T=125℉）时，用三种材料制造的电池的平均寿命差异无统计学意义。

编号为1、4、7对应的3个P值分别为0.961 6、0.999 9、0.999 1，说明当温度低（T=15℉）时，用三种材料制造的电池的平均寿命差异无统计学意义；而编号为2、5、8对应的3个P值分别为0.046 0、0.001 4、0.882 3，说明当温度居中（T=70℉）时，第一种材料与第二种材料、第一种材料与第三种材料制造的电池平均寿命（57.250 vs.119.750，57.250 vs.145.750）差异有统计学意义，而第二种材料与第三种材料制造的电池平均寿命（119.750 vs.145.750）差异无统计学意义。

相对来说，温度较低时，用第二种材料制造的电池平均寿命较长（均值为155.750）；温度居中时，用第三种材料制造的电池平均寿命较长（均值为145.750）；温度较高时，用第三种材料制造的电池平均寿命较长（均值为85.500）。

3.2.2 对例2的分析与解答

【分析与解答】所需要的SAS程序如下：

【SAS程序说明】“a|b|c”代表一种简化表达方式，其详细写法为［5］：a b c a*b a*c b*c a*b*c。

【SAS输出结果及解释】

由总模型的方差分析结果可知，总模型无统计学意义（F=1.50，P=0.163 4），说明此总模型需要精简。

由3个主效应、3个一级交互作用项效应和1个二级交互作用项效应的输出结果可知，仅交互作用项“b*c”（F=2.67，P=0.039 7）具有统计学意义。

若从模型语句中删除P值大于0.4的前4项后，再运行SAS程序，由输出结果可知，三项均无统计学意义。

由此可知，在对多因素析因设计定量资料进行方差分析过程中，随着模型中所包含的因素和交互作用项的改变，对某个特定因素或交互作用项而言，其分析的结果是会发生变化的。也就是说，方差分析的结果是相对的。

4 讨论与小结

4.1 讨论

严格地说，在对析因设计定量资料进行一元方差分析前，也应检查定量资料是否满足“独立性、正态性和方差齐性”这三个前提条件［6］。为节省篇幅，本文假定定量资料已满足此前提条件。当试验因素很多时，采用析因设计安排试验是非常耗时耗力的。一种补救措施是采用分式析因设计［1，3］或正交设计或均匀设计［2］。在析因设计的具体实施过程中，全部受试对象被完全随机分配到因素的全部水平组合中去。然而，当来自受试对象的某个或某些重要非试验因素对试验结果的影响不可忽视时，改进的做法是将受试对象按重要非试验因素形成若干个“区组”，每个区组内的受试对象在重要的非试验因素方面条件最接近、且数量等于全部试验因素的水平组合数。于是，就可参照随机区组设计的思路来随机分配受试对象［7］。这样的安排被称为“含区组因素的析因设计”［2］，此设计有利于控制区组因素对结果的影响，增加结论的可信度。

4.2 小结

本文介绍了析因设计的基本概念、析因设计的架构以及两因素析因设计定量资料一元方差分析的计算公式；通过两个实例并借助SAS软件实现了析因设计定量资料一元方差分析和关于交互作用效应的多重比较。