车辆动荷载作用下黄土地区浅埋综合管廊动力响应试验研究

段旭，刘武超，邹愈，胡兆江，董琪，叶万军

(1.西安科技大学 建筑与土木工程学院，陕西 西安 710054；2.陕西科技控股集团有限责任公司，陕西 西安 710077；3.信息产业部 电子综合勘察研究院，陕西 西安 710021)

综合管廊可有效解决路面反复开挖、架空线网密集等问题，是城市地下空间深化开发的重要战略布局，西安作为黄土地区城市综合管廊建设的先驱，已规划建设350.5 km的城市综合管廊工程。综合管廊经常从城市主干道下方穿过，容易受车辆循环荷载的影响，在地下水位较高、地表水分入渗、地下管线渗漏等情况下，水土作用更加复杂。随着近年来城市交通负荷的显著增大，综合管廊等浅埋地下工程在车辆荷载作用下的受力状态及变形防控问题也逐渐受到关注。黄土路基中车辆荷载的影响范围在0~6.5 m[1-3]左右，受车辆载重、路基路面条件的影响，在埋深小于1.2 m范围内衰减速度最快，埋深超过1.2 m则衰减趋于平缓[1]。关于车辆荷载对浅埋管道的影响，RAKITIN等[4]通过离心试验研究了管道埋深、交通荷载位置及大小对管道弯矩的影响，结果表明车辆荷载在管道正上方为最不利位置，埋深增大管道中的初始应力增加，同时交通荷载的影响减弱，在埋深4 m时管道受车辆荷载产生的弯矩仍无法忽略；ALZABEEBEE等[5]利用有限元分析对比了静载荷和动载荷作用下埋地管道的响应，认为静荷载对管道的位移影响更为显著。ALZABEEBEE等[6]基于有限元模型验证了计算交通荷载下管道的土压力计算公式的有效性，并提出了一个根据回填高度预测埋地管道上的最大土压力方程；ROBERT等[7]在有限元分析的基础上提出并验证了考虑埋地管道内外载荷的最大管道应力预测方程。随着城市综合管廊工程的建设推广，国内外学者关注到车辆载重、车速、埋深和位置等因素对综合管廊的影响。张福麟[8]利用有限元数值模拟方法，研究了在车辆荷载下管廊结构的加速度响应，发现管廊顶部受到土体和车辆荷载的总应力随埋深的增大先增加后减小；徐健等[9]通过现场试验和ABAQUS有限元数值模拟研究发现，车辆动载作用下管廊会产生明显的动位移，其增量幅值达到静载作用的33.10%；彭真等[10]通过现场足尺试验，研究了多舱综合管廊在重载车辆作用下承载力和变形能力等受力特性。综上所述，目前对于城市综合管廊等地下线性工程在考虑车辆荷载作用的研究中，多将车辆荷载进行拟静力处理，对结构与周围黄土地基的动力响应规律及其相互作用研究较少。而近年来随着城市交通负荷的增大，动载引发黄土路基动力促渗、促劣作用而加剧路面塌陷、地下构筑物损伤的问题逐渐受到关注[11-14]。本文将车辆动荷载不再拟静力处理，通过动力缩尺模型来研究车辆动荷载作用下黄土路基浅埋综合管廊的动力响应规律及其相互作用特征，为黄土地区综合管廊工程设计提供参考，也为进一步研究城市交通荷载作用下黄土路基及浅埋地下结构的工程病害防控机理提供支撑。

1 模型试验设计

1.1 模型材料与相似关系

模型试验系统由模型箱、激振加载系统和数据信息采集系统组成。模型箱尺寸为4 m×2.4 m×2.8 m(长×宽×高)，激振加载系统选用激振电机，可提供最大3 000 N的激振力，通过调整电机偏心刻度盘从而实现不同车辆荷载产生的动荷载；数据信息采集系统采用TST5915动态信息采集系统及其配套软件，试验振动响应数据采样频率为1 kHz。

综合管廊模型以支线管廊常用的单舱结构为原型，原型截面尺寸为3.0 m×3.0 m，采用预制拼装工艺施工。模型与原型几何相似比Cl为10，截面尺寸为30 cm×30 cm。原型材料为C40混凝土，选用石膏作为模型的浇筑材料，通过调节配比可以保证模型在强度上与原型材料保持弹性模量相似比为1.35。选用直径6 mm铝棒作为综合管廊模型的配筋材料，管廊模型的截面形态、尺寸及配筋如图1(a)和1(b)所示，单节管廊模型长20 cm，共7节，整体模型如图1(c)。目前相关规范未对机动车道下设管廊的最小埋深做明确要求，试验对2.0 m埋深条件下不同车辆荷载作用的影响进行模拟，结合纯黄土断面动力响应的对比，探索浅埋管廊的动力响应规律。模型土体采用取自西安地区的天然黄土，经重塑、筛分后在模型箱中逐层填筑，压实后密度为1.85 g/cm3，黏聚力为37 kPa，内摩擦角为26°。根据相似第三定律，在几何相似比与弹性模量相似比的基础上确定原型与模型的相似关系如表1所示。

图1 综合管廊模型Fig.1 Utility tunnel model

表1 模型试验各物理量相似关系Table 1 Similar ratios of physical quantities for model tests

1.2 传感器布置

为采集车辆动荷载作用下综合管廊结构与黄土路基的动态响应情况，试验采用加速度计、微型土压力盒、FBG光纤光栅应变监测仪共同组成试验监测系统。加速度传感器采用TST121A—100型压电式加速度计，灵敏度为0.01 g/mV；微型土压力盒选用ZFTY380型压力盒，灵敏度约为0.01 Pa/mV；FBG的光纤类型为石英单模光纤(SMF—28)，应变灵敏度为1.2 pm/με。

如图2所示，试验中分别在管廊内部、管廊周围土体中布置加速度计和微型压力盒，在距管廊1 m处设置对比断面。其中管廊内部加速度计等仪器均布设于管廊轴向中心位置，为监测管廊内部和外部土体加速度响应情况，在中心位置管廊顶板、侧壁、底板处设加速度计分别为gt1-1，gt1-2和gt1-3，在轴向距离20，40和60 cm处分别布设gt2-1，gt3-1和gt4-1加速度计；在距离管廊顶板、侧壁、底板10 cm的土体中布置加速度计T1-1至T1-5。在对比断面中布设加速度计T1-6，T1-7和T1-8以做对比。

图2 各传感器编号和布设位置Fig.2 Schematic of sensor number and layout position

为监测土体土压力响应变化，在上述加速度计位置逐一对应布设土压力盒s1-1至s1-8；并在管廊结构顶板、侧壁、底板外侧与土体的接触面上布设土压力盒gs1-1至gs1-4研究管廊-土接触压力响应情况。

沿管廊结构内壁底−侧−顶连续布设9个FBG光纤光栅应变监测计，以监测振动过程中管廊结构的动态应变情况，如图2(a)所示。

1.3 加载方式及工况设计

本文采用的车辆随机荷载模型为正弦波荷载，其具体表达式为[15]

式中：P0为车辆静载；P为车辆附加荷载的幅值，取值一般不超过车辆静载P0的0.3倍[16]，本文取P=0.3P0；T为车辆附加荷载的作用周期；L为轮胎接触半径，一般取15 cm；V为车辆行驶速度。

通过变换式(1)，将荷载作用时间转换到[0,T]区间上，可得[16]

试验通过调整偏心振动电机的偏心距来模拟2~10 t不同轴重车辆产生的动荷载。激振电机产生激振力公式为

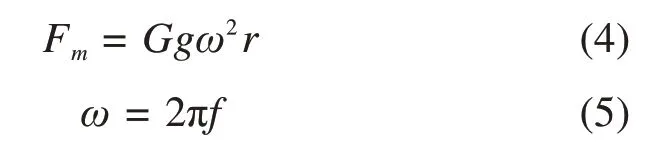
式中：G为偏心块质量；g为重力加速度；r为偏心块质心与回转轴的距离(即偏心距)；ω为电机旋转角速度；f为频率(本文f取为16 Hz)。模型试验中加载的激振力与相应工况如表2所示。

表2 工况设计Table 2 Condition design

车辆动荷载的加载位置如图2(b)所示，加载位置1位于综合管廊结构正上方，加载位置2位于距离管廊结构1 m用以对比分析。加载位置采用10 mm厚度钢板结构与振动电机刚性连接，简化模拟路面结构。

2 试验结果与分析

2.1 加速度响应分析

2.1.1 管廊周围土体及与纯土加速度对比分析

模型试验模拟了20~100 kN共5组车辆动荷载激励工况，以80 kN工况为例分析管廊周围土体的加速度时程曲线如图3所示。从图3(a)中可以看出，随着深度的增加，从管廊顶板上部土体至管廊侧壁右侧土体加速度峰值从63.25 mm/s2骤减到8.27 mm/s2，从管廊侧壁至管廊底板下方土体加速度峰值进一步减小。图3(b)为不同车辆动荷载作用下管廊周围土体加速度的峰值直方图(个别传感器数据缺失)。从图3(b)中可以看出，随着车辆动荷载的增大，各测点的加速度峰值均有所提高，管廊顶板上部土体加速度增长速率明显高于其他部位。相同车辆荷载作用下(80 kN)，管廊顶板上部土体(T1-1)的加速度值达到63.25 mm/s2，管廊侧壁土体(T1-3)、管廊底板下部土体(T1-5)的加速度响应峰值仅达到其7.9%和1.6%，管廊顶板上部土体的加速度响应幅值最为显著，影响明显大于其他位置。整体来看，20～60 kN辆动荷载作用下，地面以下20～40 cm土层的加速度响应较为明显，主要覆盖管廊顶板位置。80～100 kN车辆动荷载作用下，加速度响应范围扩展至地面以下60 cm范围内，覆盖管廊全部深度范围。

图3 (a)80 kN工况下各测点时程曲线；(b)车辆动荷载作用下管廊周围土体加速度峰值变化Fig.3 (a)Time history curve of each measuring point under 80 kN working condition;(b)Peak acceleration variation of soil around utility tunnel under vehicle dynamic load

图4为不同车辆动荷载在管廊正上部(位置1)和距管廊1 m的对比断面(位置2)处加载时，土体加速度幅值随深度变化的对比曲线，可以看出各位置土体的加速度响应峰值与车辆动荷载的增加呈较好的线性关系。通过对各组数据进行线性拟合可以发现，管廊上部土体(T1-1)加速度响应峰值随激励强度增长速率为0.87 a/kN(a为加速度单位，mm/s2)，明显大于对比断面中相近埋深的T1-6增长速率0.26 a/kN。由于加载位置1下部管廊结构的存在改变了车辆动荷载在浅层黄土路基内的传播路径，纵波在结构物与黄土的接触面产生反射，以80 kN车辆动荷载工况为例，管廊顶板上部土体的加速度响应峰值达到63.25 mm/s2明显高于对比断面中的21.00 mm/s2。

图4 车辆动荷载作用下管廊周围土体与对比断面土体加速度变化曲线Fig.4 Acceleration curve of soil around utility tunnel and comparison section under vehicle dynamic load

比较管廊底板下方土体(T1-5，埋深60 cm)和对比断面中相应位置(T1-8)的加速度响应峰值可以看出，两者随车辆动荷载增大的斜率均显著小于浅层土体。相较而言，没有埋设综合管廊的对比断面中相同深部土体的加速度峰值略大于位置1，浅埋综合管廊在提高其上部土体的加速度响应峰值的同时，减弱了车辆动荷载向管廊结构下部土体的传播。

2.1.2 管廊结构加速度分析

图5(a)反映了不同车辆动荷载作用下中心位置管廊加速度响应峰值的情况。可以看出，随着车辆动荷载幅度的增大，管廊顶板、侧壁、底板的加速度响应均呈现线性增长的趋势。由于车辆动荷载向路基深部传播过程中的能量衰减，而同时管廊结构内部空腔对车辆振动波的反射效应，管廊顶板加速度峰值随车辆动荷载变化而增长的速率分别是管廊侧壁、底板的4.3和22.4倍。以80 kN为例，管廊顶板加速度峰值分别是侧壁、底板的9.1和29.9倍。此外，管廊侧壁、底板的拟合曲线截距均接近原点，而管廊顶板加速度拟合曲线为y=0.401x+24.513，拟合直线的截距偏离原点，管廊顶板即使受到较小的振动作用即会产生较为明显的加速度响应。由图5(b)可以看出，管廊轴向距离车辆动荷载作用距离与加速度响应的关系，结果表明20～100 kN不同车辆动荷载作用下，在0～4 m范围内近线性地快速衰减，以100 kN工况为例，距离20 cm(对应原型2 m)位置的加速度响应已衰减57.88%，距离40 cm时已衰减95.93%，车辆沿管廊轴向的主要影响范围均在4 m左右。

图5 车辆动荷载作用下管廊断面加速度变化Fig.5 Variation of acceleration of utility tunnel section under vehicle dynamic load

图6分别为管廊顶板、侧壁和底板在80 kN和100 kN车辆动荷载作用下的加速度傅里叶谱。管廊各部位在0～200 Hz频段均有响应，其中管廊顶板、侧壁在频率为76.62～80.03 Hz出现频谱峰值；管廊底板的频谱峰值对应频率则在110.76 Hz左右。根据表1中的频率相似关系反算得出原型中管廊顶板、侧壁的响应频率范围为10.72～11.2 Hz，底板则在15.51 Hz左右。管廊断面各部位在不同工况下频谱峰值对应频率值如表3所示。

表3 管廊断面各部位频谱峰值对应频率Table 3 Corresponding frequency values of peak spectrum at each part of utility tunnel section Hz

图6 管廊断面各部位不同工况下的傅里叶谱Fig.6 Frequency spectrum curve of each part of utility tunnel section under different working conditions

2.2 土压力响应分析

2.2.1 管廊周围动土压力幅值分析

为分析不同车辆动荷载作用下动土压力的响应规律，如图7(a)和7(b)分别为车辆荷载在正上方激励时，管廊断面及对比断面动土压力沿深度的变化曲线。从图7(a)可以看出，管廊顶板、侧壁和底板附近土体的动土压力在车辆动荷载为20～60 kN时相差不大，各测点土压力值大致在350～1 100 Pa范围内；当车辆动荷载增加到80 kN后，管廊顶板上部和底板下部的土体土压力均出现显著增大，顶板上部(s1-1)和底板下部(s1-5)的土体土压力值为4.06 kPa和3.4 kPa，分别是管廊侧壁上、中、下(s1-2，s1-3和s1-4)位置的2.48倍，7.70倍，4.19倍和2.07倍，6.45倍和3.51倍，说明车辆动荷载为80～100 kN时，管廊顶板上部、底板下部土体的土压力值显著大于管廊侧壁土体土压力，且管廊侧壁土体土压力呈现出倒置三角形分布，侧壁中部位置动土压力幅值为最小值。

图7(b)为无管廊的对比断面土体土压力沿深度变化曲线，随着深度的增加，各车辆动荷载作用下的动土压力幅值线性减小，同时可以看出管廊结构的存在对其底板下部土体的动土压力响应有明显的放大效果。对比断面中埋深60 cm处的动土压力响应幅值仅为管廊断面相同工况的25%左右。

图7 不同车辆荷载作用下管廊周围土体土压力变化曲线Fig.7 Soil pressure curves around utility tunnel under different vehicle loads

2.2.2 管廊−土体接触压力分析

图8为不同车辆动荷载作用下管廊−土体接触压力变化曲线。随着车辆动荷载的增加，除管廊底板的管廊−土接触面(测点gs1-4)土压力值呈线性增长外，其他部位的管廊−土接触面土压力值均近似呈二次函数增加。在车辆动荷载由60 kN增大至100 kN的过程中增幅最大，而各部位的动荷载分布比例基本保持不变。以80 kN为例，管廊顶板、侧壁(上部、下部2个测点)和底板的管廊-土接触动土压力峰值分别为4.45，1.77，2.75和0.31 kPa，管廊侧壁上、下接触土压力值分别达到管廊顶板的39.8%和61.8%，与管廊侧壁附近土体动土压力峰值的倒三角分布情况相符，说明管廊顶板的土压力在车辆动荷载作用下受到的影响最大，侧壁上的土压力沿深度方向逐渐增大且小于管廊顶板的土压力，管廊底板土压力为最小。

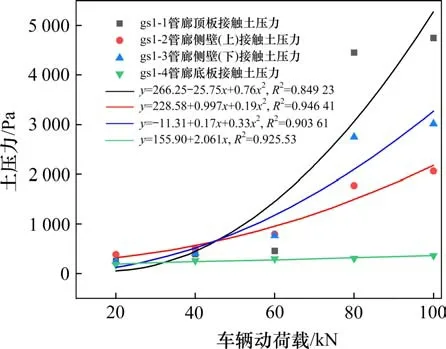
图8 车辆动荷载作用下管廊−土接触面土压力曲线Fig.8 Soil pressure curves of utility tunnel-soil contact surface under vehicle dynamic load

2.3 应变响应分析

试验通过贴在管廊内壁环形分布的FBG光纤光栅应变监测系统采集管廊结构的动态应变响应。由于车辆荷载是具有反复周期性的激振力，故各测点会产生拉、压应变交替现象，其中拉应变为正、压应变为负。图9是管廊底板、侧壁和顶板在车辆动荷载作用下的应变峰值分布情况。可以看出相同动荷载作用下管廊底板测点1，2和3拉应变起主要作用；而侧壁两端的测点4和6压应变起主要作用，中部测点5拉应变起主要作用；管廊顶板测点7和9压应变起主要作用，测点8拉应变起主要作用，可以看出动荷载激励过程中管廊顶板与侧壁类似呈现出两端受压、中间受拉的变形趋势。

图9 辆动荷载作用下管廊结构的微应变变化Fig.9 Variation of strain at bottom,side and top of utility tunnel under vehicle dynamic load

如图10所示，各测点动应变响应的最大绝对值及其方向可反映该部位的主要应力状态。可以看出，随着车辆动荷载的增加，各测点整体应变峰值整体增大；管廊底板测点1→3，应变逐渐减小，说明动荷载激励过程中管廊结构表现出非对称的变形状态。管廊侧壁呈现两端受压、中间受拉，并且管廊侧壁下部的测点4的受压程度大于侧壁上部的测点6。管廊顶板呈现两端受压、中间受拉的状态，同样表现出一定的非对称分布状态，测点7的压应变幅值在整个结构中最大，在顶板与侧壁掖角部位出现一定的应力集中现象，最大压应变51.4με，远低于混凝土材料抗压极限应变。最大拉应变23.9με，对于原型C40混凝土材料来说仍处于100με左右的弹性拉应变范围内[17]，符合混凝土结构设计规范要求。但在多项荷载耦合作用中车辆动荷载引起的局部拉应变不可忽略。

图10 车辆动荷载作用下各测点最大微应变变化曲线Fig.10 Maximum micro strain curves of each measuring point under vehicle dynamic load

3 结论

1)随着车辆动荷载强度的提高，黄土路基的动力响应范围由20 cm逐渐扩大至地面以下60 cm(对应原型原型6 m)的范围内，覆盖率浅埋管廊埋深范围。同时浅埋管廊顶板上部土体的加速度响应较纯黄土断面呈现出明显的放大效应。

2)车辆动荷载作用下，管廊顶板部位的加速度响应幅度最大，以80 kN为例，管廊顶板的加速度响应峰值分别是侧壁、底板的9.1和29.9倍。管廊顶板、侧壁频谱峰值对应频率为76.62～80.03 Hz(对应实际为10.72～11.2 Hz)，而管廊底板对应的频率增加到110.76 Hz左右(对应实际为15.51 Hz)。

3)当车辆动荷载较弱(小于60 kN)时，管廊周围土体的动土压力响应幅值差异较小，车辆荷载达到80 kN及以上后，管廊顶板、底板临近土体的动土压力响应幅值显著增大。管廊顶板、侧壁各部位与土体的接触压力随着车辆动荷载的提高符合二次函数模型。

4)车辆动荷载作用下，管廊底板以拉应变为主，侧壁和顶板呈现出两端受压、中间受拉的应变分布特征，管廊结构呈现并非对称动态应变分布的同时在顶板与侧壁掖角部位出现一定的应力集中现象。