气候变暖条件下寒区隧道可靠性分析

辛成平，贾剑青，贾超，张帮鑫

(1.兰州交通大学 交通运输学院，甘肃 兰州 730070；2.广东盛翔交通工程检测有限公司，广东 广州 511400)

我国冻土分布十分广泛，冻土面积约占全国陆地总面积的75%，其中青藏高原冻土面积约占60%。随着我国经济社会快速发展和“一带一路”倡议的推进，我国在冻土区修建了大量寒区隧道。然而，由于冻害影响，部分已建寒区隧道工程全年有8～9个月不能投入正常使用。温度环境是影响寒区隧道长期稳定性和可靠性的关键因素；气温的升高，将导致寒区隧道工程围岩冻融范围扩大以及冻胀压力增加，进而引起工程稳定性下降，该灾变过程对工程安全产生严重影响[1]。近年来，国内外专家学者针对寒区隧道稳定性开展了大量研究工作。严健等[2]提出了寒区裂隙冻岩隧道的宏观冻胀力理论模型；王道远等[3]揭示了隧道局部存水冻胀作用机制，建立了衬砌结构安全性评价方法；夏才初等[4−5]推导了寒区隧道围岩最大冻结深度解析计算公式；李又云等[6]基于多场耦合数值分析，研究了最大冻深条件下冻胀力的变化规律；LIU等[7]提出了考虑围岩弹性模量和孔隙比时隧道围岩冻胀压力的损伤模型；NISHIMURA等[8]建立了冻融条件下饱和土的水热力耦合模型，并模拟分析了某饱和冻土区管道的热力学特性；李思等[9]针对围岩导热系数、比热容和赋存温度等因素，分析了寒区隧道温度场的敏感性；杜耀辉等[10]研究了电伴热系统对季节性寒区隧道温度场分布规律的影响；LI等[11]建立了寒区隧道水热耦合模型，确定了冻土隧道不受冻融破坏时保温层的最佳厚度；LAI等[12−13]分析了现有隧道防冻保温方法的适用性，并提出了利用地热能及电伴热系统进行隧道隔热防冻的优化设计方法。青藏高原气温升高是对全球气候变暖的响应，秦大河等[14]认为未来50年青藏高原气温将升高2.6℃；IPCC第5次评估报告认为：21世纪中后期全球平均温度将上升2.0℃，第三极气温在以全球平均气温2倍的速度变暖；IPCC《全球1.5℃增暖特别报告》中将全球平均气温上升控制在1.5℃内(第三极为3.0℃)为目标。因此，本文以青藏高原某寒区隧道为背景，分析研究青藏高原气候升高2.6℃，3.0℃和4.0℃时隧道温度场和变形场的时变特点以及可靠性的演化规律，对寒区隧道工程设计和灾害防治等具有参考价值。

1 工程概况

巴哈达坂隧道位于青海省门源县，隧道左线起讫点桩号ZK84+620～ZK89+585，全长4 965 m；右线起讫点桩号ZK84+575～ZK89+575，全长5 000 m。隧道左、右线最大埋深分别为580 m和600 m，隧址区多年平均气温−3.1℃以下，历年极端最高气温为35.6℃，极端最低气温为−34℃；该隧道为季节性冻土隧道，最大冻深为2 m。

巴哈达坂隧道围岩等级以IV级和V级为主，洞身衬砌采用以锚杆、钢筋网喷混凝土和钢拱架为初期支护，模筑混凝土或钢筋混凝土为二次支护的复合支护结构；初期支护采用C25混凝土，二次衬砌为C30混凝土；隧道进出口800 m范围内铺设5 cm厚的聚酚醛泡沫保温材料；隧道断面如图1所示。根据试验测试并结合相关文献的研究成果[15]，确定巴哈达坂隧道围岩及支护结构物理力学参数如表1所示。

表1 围岩及支护结构物理力学参数Table 1 Physical and mechanical parameters of surrounding rock and supports

图1 隧道断面Fig.1 Tunnel section

2 寒区隧道稳定性分析

2.1 模型建立

模型中，隧道埋深为实际埋深，即埋深为32 m，左右边墙到边界的距离均为25 m，底板到下边界的距离为35 m，隧道断面尺寸按图1选取。模型网格划分采用映射划分方法；围岩和支护结构物理力学参数见表1；模型网格划分如图2所示。

图2 模型网格图Fig.2 Meshing diagram

模型A C边和BD边均为水平位移约束，CD边为固定边界条件，A B边为自由边界条件。模型A C边和BD边均为绝热边界，CD边为热流边界，热流密度为0.06 W/m2，AB边和EF G H边为对流换热边界，对流换热系数为15.0 W/(m2·℃)。材料热力学参数如表2所示。

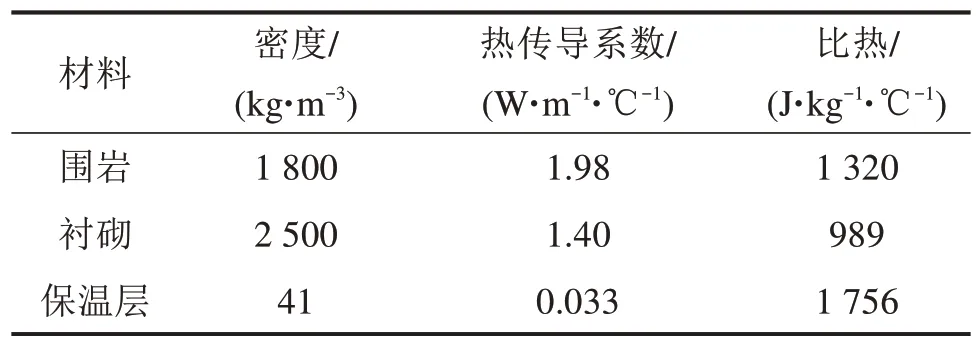
表2 热力学参数Table 2 Thermodynamic parameters

A B边温度为：

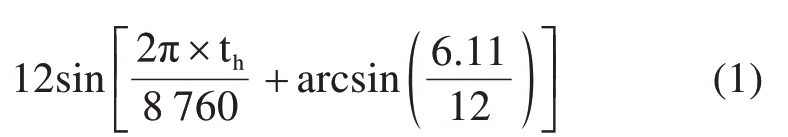
式中：Ti为模拟温度，即分别为2.6℃，3.0℃和4.0℃；th为时间，h。

隧道内壁E F GH温度为：

2.2 模拟结果分析

2.2.1 2.6℃应力场

气温升高2.6℃时隧道应力场模拟结果如图3所示；应力和位移变化曲线如图4所示。

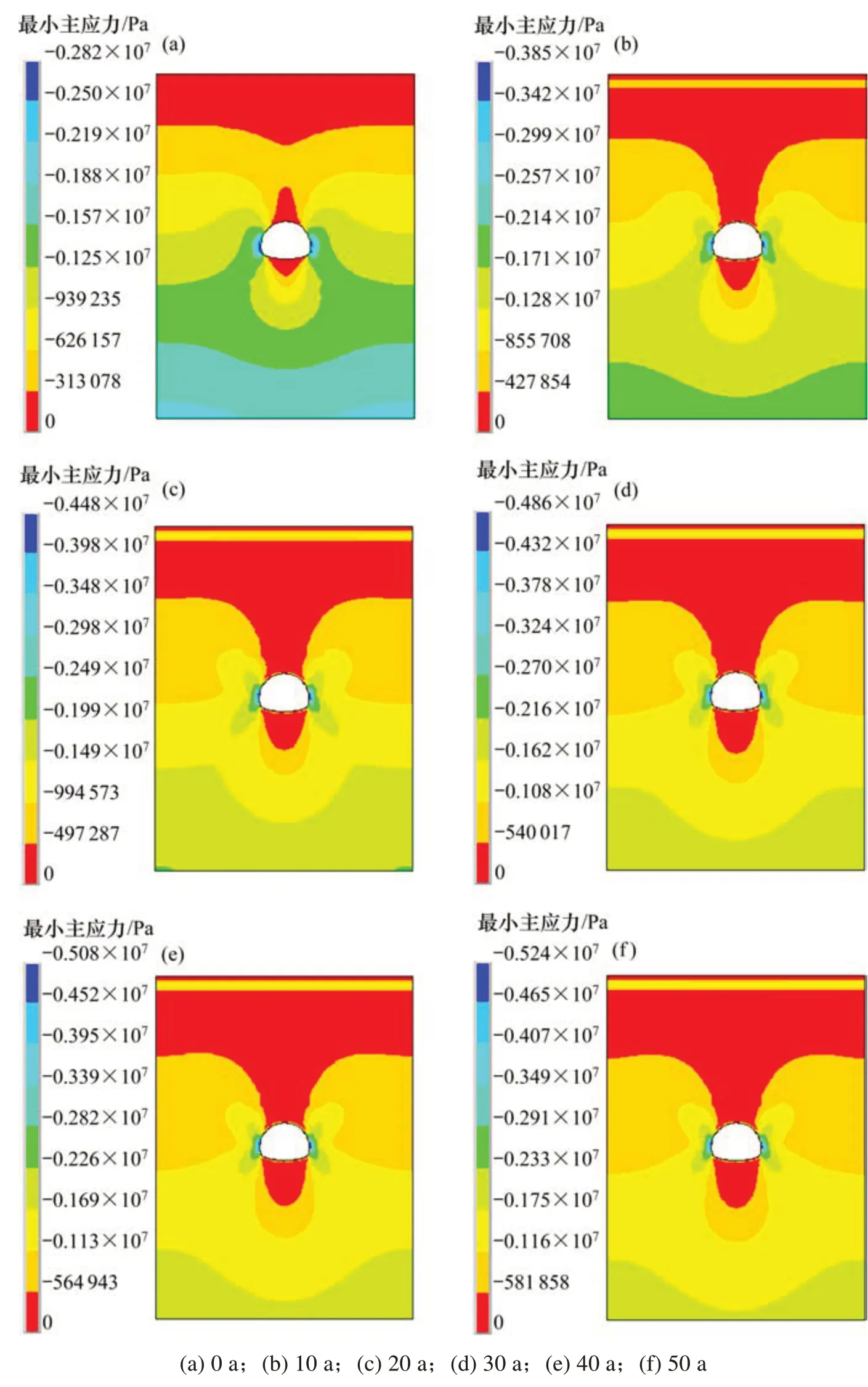
图3 2.6℃最小主应力云图Fig.3 2.6℃minimum principal stress nephogram

图4 2.6℃应力及位移变化曲线Fig.4 2.6℃stress and displacement variation curves

从图3和图4可知，温度升高2.6℃时，起始年拱顶、边墙和墙角的竖向位移分别为−4.65，−3.74和−3.02 mm，而仰拱处存在底鼓现象，其位移为2.55 mm；起始年最大压应力为2.82 MPa，发生在隧道墙角处。随着时间推移，隧道应力和位移均不断增大，但前30年变化比较明显，其后逐渐趋于平缓。第30年拱顶、边墙、墙角和仰拱竖向位移分别为−8.62，−6.90，−6.13和5.49 mm，相较第0年分别增长了85%，84%，103%和115%；第30年最大压应力为4.86 MPa，相较起始年增长了72%。第50年拱顶、边墙、墙角和仰拱处竖向位移分别为−9.82，−7.45，−6.75和6.25 mm，相较第30年分别增加了14%，8%，10%和14%；第50年隧道最大压应力为5.24 MPa，相较第30年增加了8%。

2.2.2 3.0℃应力场

气温升高3.0℃时隧道应力场模拟结果如图5所示；应力和位移变化曲线如图6所示。

从图5和图6可知，温度升高3.0℃时，起始年拱顶、边墙和墙角的竖向位移分别为-4.65，-3.80和-3.06 mm，而仰拱处存在底鼓现象，其位移为2.61 mm；和2.6℃的结果比较可知，同期拱顶、边墙、墙角和仰拱竖向位移分别增加了0%，2%，1%和2%。起始年最大压应力为2.83 MPa，相较2.6℃同期增加了0.3%。第30年拱顶、边墙、墙角和仰拱竖向位移分别为-8.69，-7.12，-6.31和5.65 mm，相比于增温2.6℃同期分别增加了0.8%，3%，3%和3%；第30年最大压应力为4.89 MPa，相较2.6℃同期增加了0.6%。第50年拱顶、边墙、墙角和仰拱处竖向位移分别为-9.90，-7.72，-6.95和6.37 mm，比增温2.6℃同期分别增加了0.8%，4%，3%和2%；第50年隧道最大压应力为5.32 MPa，比增温2.6℃同期增加了2%。

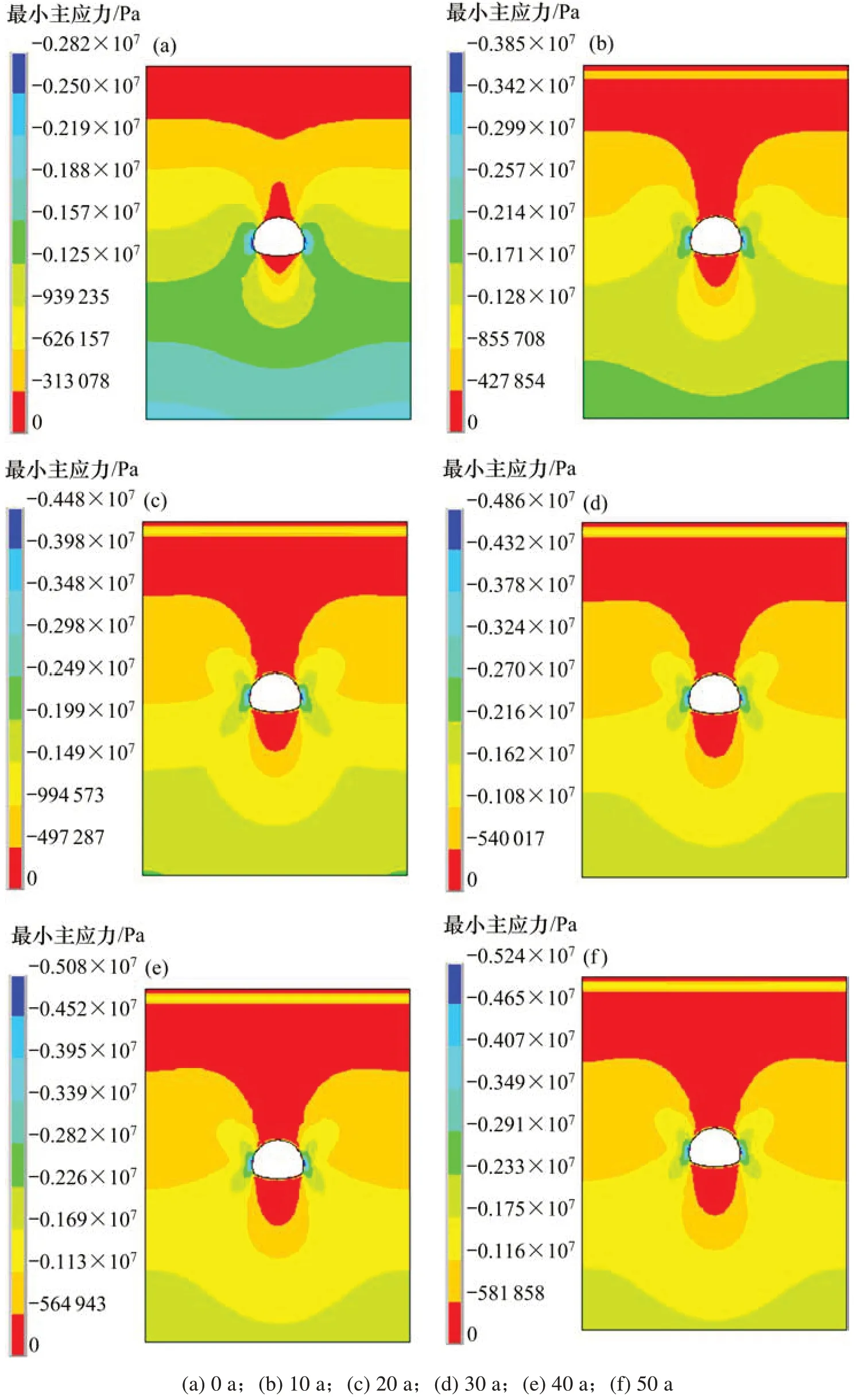
图5 2.6℃最小主应力云图Fig.5 2.6℃minimum principal stress nephogram

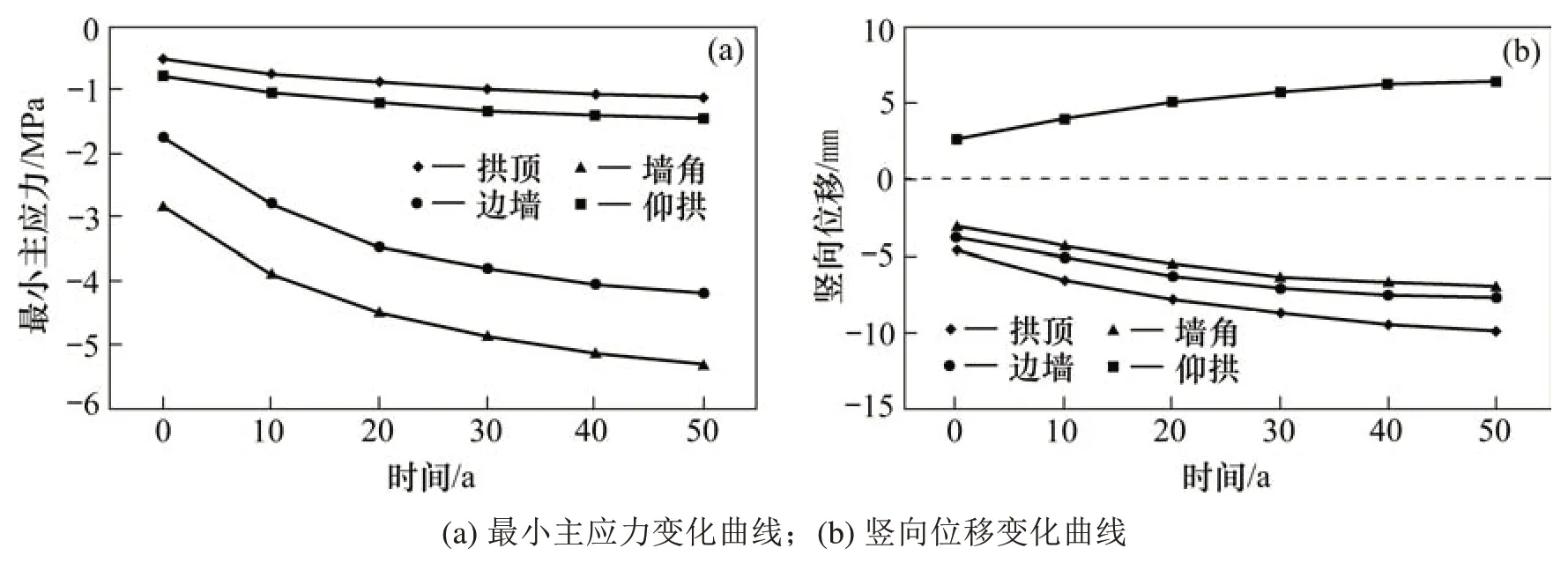
图6 3.0℃应力及位移变化曲线Fig.6 3.0℃stress and displacement variation curves

2.2.3 4.0℃应力场

气温升高4.0℃时隧道应力场模拟结果如图7所示；应力和位移变化曲线如图8所示。

从图7和图8可知，温度升高4.0℃时，起始年拱顶、边墙、墙角和仰拱竖向位移分别为-4.72，-4.04，-3.23和2.90 mm，由于仰拱处竖向位移向上且其值较大，大大增加了隧道底鼓风险；和2.6℃的结果比较可知，同期拱顶、边墙、墙角和仰拱竖向位移分别增加了2%，8%，7%和14%。起始年隧道最大压应力为2.86 MPa，相较2.6℃同期增加了2%。第30年拱顶、边墙、墙角和仰拱的竖向位移分别为-8.86，-7.65，-6.65和6.15 mm，相比于增温2.6℃同期分别增加了3%，11%，8%和12%；和起始年相比，第30年各处竖向位移分别增加了88%，89%，106%和112%。第30年隧道最大压应力为5.03 MPa，相较2.6℃同期增加了3%。第50年拱顶、边墙、墙角和仰拱竖向位移分别为-10.1，-8.83，-7.34和6.56 mm，相较第30年分别增加了14%，15%，10%和7%，比增温2.6℃同期分别增加了3%，19%，9%和5%；第50年隧道最大压应力为5.60 MPa，相较第30年增加了11%，比增温2.6℃同期增加了7%。

图7 3.0℃最小主应力云图Fig.7 3.0℃minimum principal stress nephogram

图8 4.0℃应力及位移变化曲线Fig.8 4.0℃stress and displacement variation curves

3 寒区隧道可靠度分析

3.1 可靠性基本理论

可靠度是指结构在规定条件和规定时间内完成规定功能的概率。实际工程中，通常将基本变量视为作用效应R和结构抗力S，则结构功能函数为：

当Z>0时，表示系统处于可靠状态；Z<0时，表示系统处于失效状态；Z=0，表示系统处于极限状态。

由于R，S和Z是随机变量，且当R和S的统计参数确定后，Z的统计参数也能唯一确定。巴哈达坂隧道初期支护、二次衬砌和围岩物理力学参数概率分布特征如表1。

假设R和S均服从正态分布且相互独立，则Z也服从正态分布，其均值为μZ，标准差为σZ，此时Z的密度函数为：

3.2 可靠性分析

本文将隧道围岩和初期支护的杨氏模量、密度、泊松比和二次衬砌厚度、杨氏模量、密度、泊松比设为随机输入变量，将隧道衬砌结构的最小主应力视为随机输出变量，采用蒙特卡罗法计算分析隧道可靠度的变化特征。本文经过10 000次模拟计算即得历史样本曲线及可靠性分布函数曲线，其中气温升高2.6℃的最小主应力样本历史曲线及可靠性累积分布函数曲线如图9所示。2.6℃，3.0℃和4.0℃时隧道可靠度指标如图10所示。

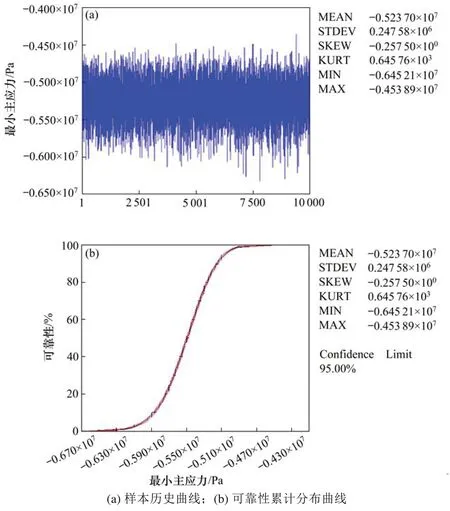
图9 2.6℃最小主应力Fig.9 Minimum principal stress at 2.6℃

图10 可靠度指标和失效概率Fig.10 Reliability index and failure probability

从图10可知，气温升高2.6℃，3.0℃和4.0℃时，巴哈达坂隧道可靠度指标随时间推移而减小，亦即失效概率随时间推移而增大，且升温越快，同期内隧道可靠度指标下降越快，也就是说隧道出现冻胀等病害的概率大大增加。气温升高2.6℃时，30年后隧道可靠性约为91.5%，可靠度指标为1.405，而气温升高4.0℃时其可靠性降至88%，可靠度指标减小到1.175。

如果将21世纪中后期第三极温度控制在3.0℃以内，30年后巴哈达坂隧道可靠性可达90.5%，可靠度指标为1.31，同时期可靠性指标比气温升高4.0℃时增加了0.135，失效概率降低了2.5%。50年后，气温升高2.6，3.0和4.0℃时的可靠度指标分别为1.15，1.08和0.924，可靠性分别为87.5%，86%和82.2%。

3.3 敏感性分析

模拟所得气温升高2.6℃时巴哈达坂隧道最小主应力敏感性如图11(a)所示。

由图11可知，初期支护、围岩和二次衬砌杨氏模量以及二次衬砌厚度和泊松比对隧道最小主应力的影响显著。工程设计中，衬砌结构的杨氏模量可视为常量，则可通过调整二次衬砌厚度以改变最小主应力大小，进而实现隧道工程目标可靠度。隧道支护结构最小主应力与二次衬砌厚度间的散点图如图11(b)所示。

图11 2.6℃最小主应力敏感性Fig.11 Sensitivity of maximum compressive stress at 2.6℃

结合图11(b)最小主应力累计分布曲线可知，要保证2.6℃时隧道可靠性在90%以上，其最小主应力应小于5.11 MPa，二次衬砌最小厚度为46.5 cm。通过对图9(b)的拟合分析所得气温升高2.6℃时，第50年巴哈达坂隧道最小主应力σ3与二次衬砌厚度ERCHENTH间的函数关系为：

同样，拟合所得气温升高3.0℃和4.0℃时最小主应力与二次衬砌厚度的关系式分别如式(9)和式(10)所示。

若要将巴哈达坂隧道的可靠性确保在90%以上，通过式(8)，式(9)和式(10)计算所得气温分别升高2.6℃，3.0℃和4.0℃时，保温层和二次衬砌最小厚度如表3所示。

表3 保温层和二次衬砌最小厚度Table 3 Minimum thickness of secondary lining and insulation layer

从表3可知，在同一升温条件下，所需最小二次衬砌厚度随保温层厚度的增加而减小；气温升高2.6℃和3.0℃，当保温层厚度大于7 cm时，为确保50年后隧道可靠性在90%以上所需最小二次衬砌厚度基本保持不变；而气温升高4.0℃时，当保温层厚度大于9 cm，所需最小二次衬砌厚度也基本保持不变。因此，根据《全球1.5℃增暖特别报告》建议，若21世纪中后期将全球升温控制在1.5℃以内(第三极升温控制在3.0℃以内)，当隧道保温层厚度为8 cm，二次衬砌厚度不小于42.7 cm时，即可确保50年后隧道的可靠度在90%以上。

4 结论

1)随着时间推移，隧道应力场和位移场均不断增加，但是前30年增幅比较明显，其后逐渐趋于平缓。

2)由巴哈达坂隧道可靠度分析可知，在现有设计条件下，50年气温升高2.6℃和4.0℃时隧道可靠度分别为87.5%和82.2%。

3)敏感性分析表明，保温层厚度和二次衬砌厚度对隧道可靠度敏感性显著。

4)要将50年后隧道可靠度保持在90%以上，气温升高2.6℃时二次衬砌和保温层最小厚度为42.3 cm和7 cm，比现有设计分别提高了6%和40%；而气温升高4.0℃时二次衬砌和保温层最小厚度分别达到45.2 cm和9 cm，比现有设计提高了13%和80%。

5)根据IPCC结论，如果未来50年将第三极升温控制在3.0℃内，当保温层厚度为8 cm，二次衬砌厚度不小于42.7 cm时，隧道可靠度即可达90%以上。