基于遗传禁忌算法的城市轨道交通乘务任务配对研究

薛 锋 ，李 海，梁 鹏，陈崇双，罗 建

（1.西南交通大学 交通运输与物流学院，四川 成都 611756；2.西南交通大学 综合交通运输智能化国家地方联合工程实验室，四川 成都 611756；3.西南交通大学 综合交通大数据应用技术国家工程实验室，四川 成都 611756；4.西南交通大学 数学学院，四川 成都 611756；5.西华大学 汽车与交通学院，四川 成都 610039)

0 引言

城市轨道交通乘务计划是指导乘务员日常工作的核心文件，长期以来该计划都采用人工编制，效率比较低，各项参数设置也较为主观，配置结果往往出现人员紧张或者人员闲置情况，稳定性较差，且随着城轨线路、客运需求的不断增加，人工编制的方法已难以满足实际需求，如何快速编制高效的乘务计划并进行优化成为亟待解决的问题。

目前，我国城市轨道交通乘务计划普遍分为乘务任务配对和乘务任务轮转2 个子问题。乘务任务配对，是根据相应线路条件、运营约束将列车运行计划以轮乘点为分割点进行拆分，结合乘务员值乘约束，组合配对形成乘务任务。乘务任务轮转指将配对好的早、白、夜3种不同班种的乘务任务，按照轮转制度，较为均衡地安排给每个乘务员，从而形成乘务员的阶段任务。这其中乘务任务配对是首要环节，更是编制乘务轮转计划的前提。张增勇等[1]基于惩罚费用构建了乘务排班双层优化模型，并设计了Dijkstra 算法和离散粒子群算法求解，但模型的目标函数计算复杂，得到的乘务方案间休时间仍高于标准时间；丰富等[2]从时间均衡度角度研究了乘务排班计划优化问题，但目标函数中的权重系数较难确定；Fuentes 等[3]考虑每个乘务任务的总时间，建立了基于排序的乘务任务配对模型(SEBACS)，并设计了拉格朗日松弛算法进行求解；胡汪源[4]和袁仁杰[5]将乘务排班问题归结为VPR问题，并分别从减少乘务费用和等待时间、减少乘务任务数量和均衡工作量2 个角度，对乘务排班问题进行优化研究；马卓然[6]和金华等[7]从资源共享角度即不同线路间列车不跨线情况下的乘务员可共享角度对乘务排班问题进行优化研究；石俊刚等[8]和许仲豪等[9]基于列生成思想，分别结合跟随分支策略和贪婪算法对乘务排班问题进行研究；马亮等[10]考虑实际便乘情况，以乘务任务数量最少为目标，建立了乘务任务配对的约束优化模型，并设计约束传播与启发式回溯的混合算法，得到在求解质量和求解效率方面都比现场和不带约束传播的深度优先回溯算法高的排班方案。

现有研究主要是基于集合分割与集合覆盖思想，建立相应的乘务排班优化模型，然后采用列生成算法或启发式算法进行求解，得到满足约束条件下的乘务排班方案。但是，既有研究都是在假定各时间参数已知情况下进行乘务计划编制，而在实际编制过程中，这些参数并非都是已知的，且其中任何一个参数的变化都可能影响最终乘务计划编制的效果。为此，研究参数未知情况下的城市轨道交通乘务任务配对问题，以一日内所有乘务员的效率最大化为目标，建立混合整数规划模型，并设计与之匹配的遗传禁忌混合搜索算法。

1 问题描述

为了方便描述乘务排班问题，有必要对几个概念进行说明。地铁运营部门固定选择几个车站作为司机值乘换班的地点，称之为轮乘站。实际中，一般将车辆段、停车场、某些车站作为轮乘站。车辆段和停车场一般选择在线路的两端，处于线路中间的轮乘站一般基于值乘负荷进行设置。相邻两个轮乘站之间的距离一般不会太远，否则连续工作时间太长，容易致使司机驾驶疲劳；相邻两个轮乘站之间的距离一般也不会太近，否则司机们的工作效率不高。运行线上连续两个轮乘站之间的线段，即是乘务任务作业段。每个司机一般会值乘多个乘务任务作业段。因此，几个乘务任务作业段的集合，称之为乘务任务，顾名思义，对应了一名司机的值乘任务。

在给出上述3 个概念的基础上，给出乘务任务配对问题描述。所谓乘务任务配对指将给定的列车运行计划(即列车运行图)依据轮乘站划分成若干乘务作业段，然后再将乘务作业段组合成乘务任务，每个乘务任务由一个乘务员一天内完成。此处以一个简单的案例进行说明，乘务任务配对示意图如图1 所示。

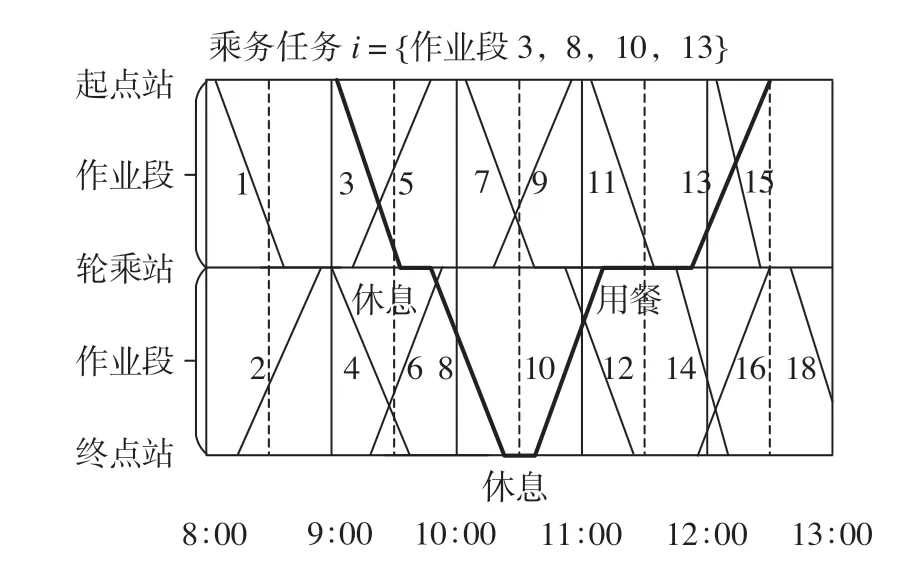
图1 乘务任务配对示意图Fig.1 Schematic diagram of crew task pairing

假设该线除起点站、终点站外，只有一个中间轮乘站，按照地铁公司要求，当列车经过起点站、终点站、轮乘点时，乘务员需要休息，不能跨过轮乘站进行连续值乘，从而保证每位乘务员连续工作时间不超过限值。同时，当乘务员工作时段处于用餐时段时，必须为乘务员安排时间用餐，提供就餐的地点只能在起点站、终点站和轮乘站。假设中午用餐时间为11 :00—13 :00，则按照乘务作业段划分规则，乘务作业段包括2 种，分别为：起点站轮乘站，终点站轮乘站。结合休息时间约束、用餐时间约束、列车整备等约束，配对好的一个乘务任务如图1 中粗实线所示，而实际中的乘务任务配对问题便是在案例基础上，将所有的乘务作业段在符合约束的情况下配对形成特定的乘务任务，从而使得整个列车运行计划能够被完整的执行。

2 数学模型

2.1 目标函数

以一个工作日内全部乘务员的值乘效率最高为优化目标。对于每一位乘务员，其乘务任务的时间为值乘作业段的时间、休息时间、用餐时间等多个环节的时间总和，最大化值乘效率即最大化值乘时间占整个乘务任务时间的比重。因此，城市轨道交通乘务配对模型的目标函数如下。

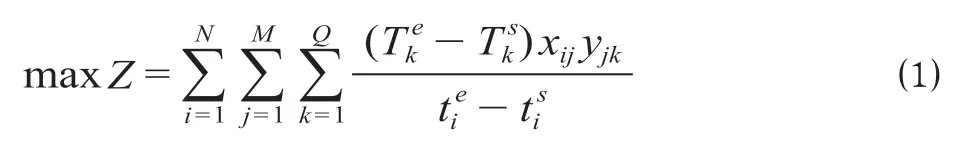
式中：N为一日内乘务员总数，人；M为乘务任务总数，个；Q为乘务任务包含的乘务作业段总数，个；为第k个乘务作业段的结束时间；为第k个乘务作业段的开始时间；为第i个乘务员工作结束时间为第i个乘务员工作开始时间；xij表示第i个乘务员是否值乘第j个乘务任务，值乘取1，否则取0；yjk表示第k个乘务任务作业段是否属于第j个乘务任务，属于取1，否则取0。

同时为方便计算，以第i个乘务员值乘的第一个乘务作业段开始时间为工作开始时间，以第i个乘务员值乘的最后一个乘务作业段结束时间为工作结束时间。

2.2 约束条件

2.2.1 乘务员与乘务任务间的值乘约束

在乘务任务配对过程中，乘务员与乘务任务之间存在相互唯一的对应关系，即第j个乘务任务只能由其中一个乘务员值乘，第i个乘务员也只能值乘一个乘务任务。

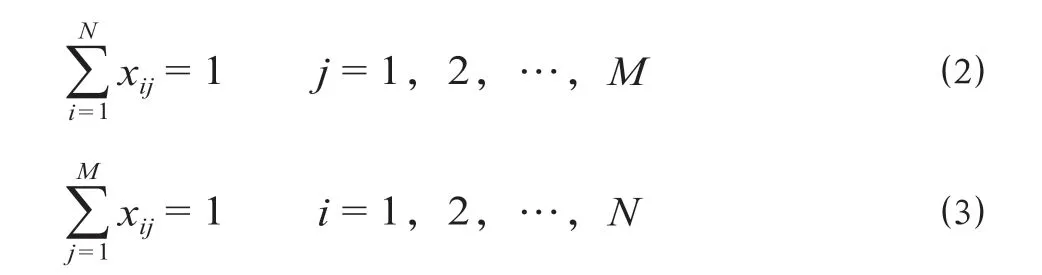
2.2.2 乘务员工作起止时间约束

对每个乘务员来说，所值乘的任意乘务作业段开始时间均不能早于其工作开始时间，同时，所值乘的任意乘务任务段结束时间不能晚于其工作结束时间。

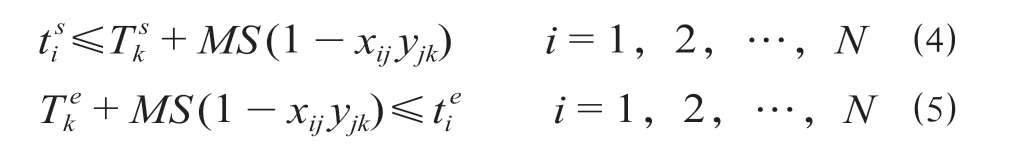
式中：MS为较大的正常数。

2.2.3 工作时间上限约束

根据劳动法规定，每个乘务员一天内的工作时间总长不能超过相应工作班次的上限。早班、白班、晚班的工作时间上限约束分别如下。

2.2.4 休息时间约束

在非用餐时间段，即当前值乘的乘务任务作业段从开始到结束的时间区间与用餐时间区间无交叉，那么，乘务员在完成相邻两个乘务作业段的值乘任务时，必须安排时间休息，以避免长时间值乘导致乘务员疲劳驾驶。休息时间不能过短，否则乘务员无法缓解疲劳、恢复精力，因而休息时间有一个下限，同时休息时间也不能过长，导致工作效率低下，故休息时间也必须有一个上限。该约束条件为当

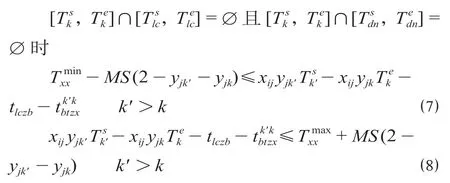
式中：为午餐开始时间；为午餐结束时间；为晚餐开始时间；为晚餐结束时间；为最短休息时间，h；为最长休息时间，h；tlczb为列车整备时间，h时间为轮乘站k′与k之间的接续，h。

整备时间及不同值乘点接续时间具体计算公式如下。

（1）整备时间的计算公式为

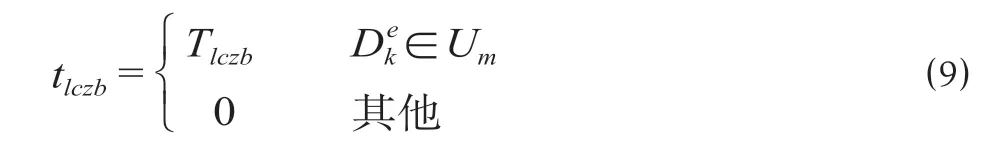
式中：Tlczb为相应地铁运营公司整备时间标准，h；Um为车辆段地点集合；为第k个乘务作业段结束地点。

（2）不同值乘点之间所需的接续时间。当需要值乘点与乘务员当前地点不同时，必须通过其他交通工具或便乘到达指定值乘地点。当值乘点不同时，需要的接续时间计算公式为

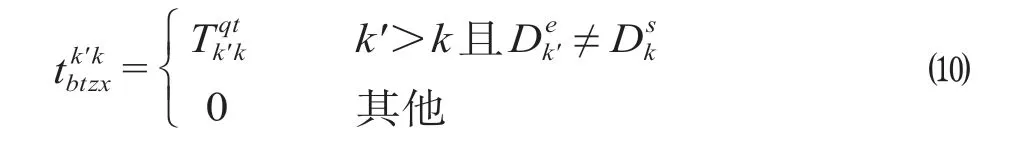
式中：为第k个乘务作业段开始地点；为第k′个乘务作业段结束地点；为前后值乘点不同时，通过便乘到达指定值乘地点所需时间，h。

2.2.5 用餐时间约束

当乘务任务的工作时间段覆盖用餐时段时，即当前值乘的乘务任务作业段从开始到结束的时间区间包含或部分包含用餐时间区间，那么，必须在指定轮乘站预留充足的时间为乘务员安排用餐，通常只考虑午餐和晚餐。该约束具体刻画如下，当∅时

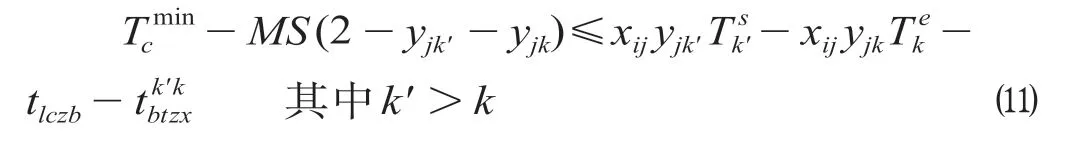
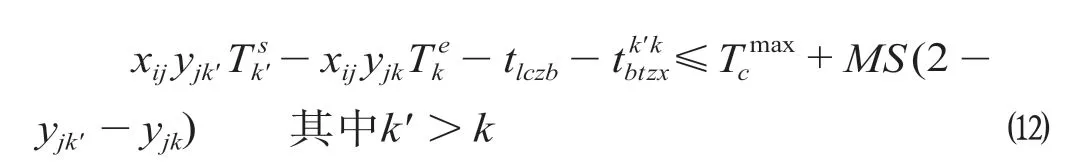
式中：为最短用餐时间，h；为最长用餐时间，h。

以上约束中用餐时间与休息时间不能同时存在，即若值乘时间覆盖用餐时间段，就必须安排用餐，否则就安排休息。

3 算法设计

由建立的模型以及相关约束条件可知，该模型是一个非线性的混合整数规划模型，涉及参数较多，如休息时间上下限、用餐时间上下限、各班次最长工作时间等，且各参数的选择具有很大的范围，为此针对建立的乘务任务配对模型，设计遗传禁忌混合搜索算法进行求解，步骤如下。

步骤1：根据地铁运营公司指定的轮乘站，结合乘务员连续值乘约束，将列车运行任务划分为以轮乘站为分割点的乘务作业段，同时依据乘务作业段开始时间，对乘务作业段进行排序。

步骤2：给出模型涉及参数个数YCJJNcs，本模型中该值为13，依据划分刻度，对各参数进行划分，得到其对应节点数，依据解空间规模给出种群个体数YCJJnum，最大迭代次数YCJJTT，交叉概率YCJJpc，变异概率YCJJby。

步骤3：依据YCJJNcs，各参数节点数及种群个体数，随机产生初始种群。每个种群中个体的产生方式如下，如模型中有13 个参数，那么基因编码长度即为13，假设第一个基因对应参数为休息最少时间，该参数可变区间为8～15 min，依据该参数1 min 划分刻度，得到节点共有8 个，那么第一个基因位的值即为随机产生1—8 的随机数，其余基因位同理，据此，产生该个体染色体的全部基因，按照此规则，产生该种群所有个体的染色体。同时初始化禁忌表，大小为YCJJTT×YCJJNcs的全0 矩阵，最大效率记录表，大小为YCJJTT×1的矩阵，最大效率对应参数记录表，大小为YCJJTT×YCJJNcs，初始化a=1，b=1。

步骤4：记录当前迭代次数a，如果a≤YCJJTT，转步骤5，否则，依据解码规则，输出效率最高的乘务任务对应的染色体解码得到的各个参数时间值及相应乘务任务效率，绘制最高效率随迭代次数a的变化图。

步骤5：从种群中第b个体开始，b≤YCJJnum，依次代入当前种群中该个体染色体对应的参数值，代入方式如下：如步骤3 中，第一个基因位对应休息最少时间，产生的随机数为5，即对应第5 个时间节点12 min，那么以8 min 减去时间划分刻度值，即7 min 对应时间420 s 为基础，加上1 min 时间刻度对应时间60 s 乘以该随机数5，即得到该基因位对应实际参数值12 min。其余各参数代入方式相同，只是各参数代入时的基础时间以及跨度时间依据各参数特征而有所不同。代入后基于贪婪算法思想，从第一个乘务作业段开始，依据休息时间约束、用餐时间约束，同时考虑前后值乘点不同时便乘的情况，在该乘务作业段当前的所有可接续作业段中找出接续时间最短且没有组合过的乘务作业段，进行组合。然后对被组合乘务作业段做同样的操作，直到乘务班次时间达到工作时间上限或不存在可接续乘务作业段时，记录该班次的乘务作业段组合方式。

步骤6：依次从剩余没有进行组合的乘务作业段中，找出开始时间最早的乘务作业段，执行步骤5 中的组合配对操作，直到所有乘务作业段都被分配到不同的乘务班次中。

步骤7：令b=b+1，如果b≤YCJJnum，转步骤5，否则转步骤8。

步骤8：计算当前种群所有个体编制出的乘务任务效率，并将效率最高值的个体参数记入禁忌表，若a=1，则将该效率值记录为第a代最高效率，否则将效率最高值与第a-1 代最高效率进行比较，若当前种群最高效率大于第a-1 代最高效率，则将当前种群最高效率值赋值给第a代最高效率，同时记录该个体参数值；否则，记录第a代最高效率等于第a-1 代最高效率，第a代最高效率对应参数表值不变。

步骤9：依据给定的交叉概率、变异概率，对种群进行选择、交叉、变异操作，同时为扩大算法搜索范围，避免算法陷入局部最优解，在每一代种群中，随机产生1/3 的新种群，加入子代种群中，并将种群个体与禁忌表进行比较，剔除禁忌表中已经存在的个体。

步骤10：令a=a+1，b=1，转步骤4。

4 实例分析

成都地铁5 号线北起新都区华桂路站，途径金牛区、青羊区、武侯区，南至双流区回龙站，全长49.02 km，共设41座车站。为满足该线运营需求，共划分8 个轮乘站点，含1 个车辆段，2 个停车场，成都5 号线轮乘点设置如图2 所示。取其中一日内的运行图数据进行算例分析，该数据共包含686 个乘务任务作业段，乘务任务作业段数据如表1 所示，其中8 个轮乘点分别用X1—X8 来表示，对应关系X1 →大丰停车场，X2 →华桂路，X3 →石犀公园，X4 →福宁路，X5 →元华车辆段，X6 →二江寺，X7 →回龙站，X8 →回龙停车场。

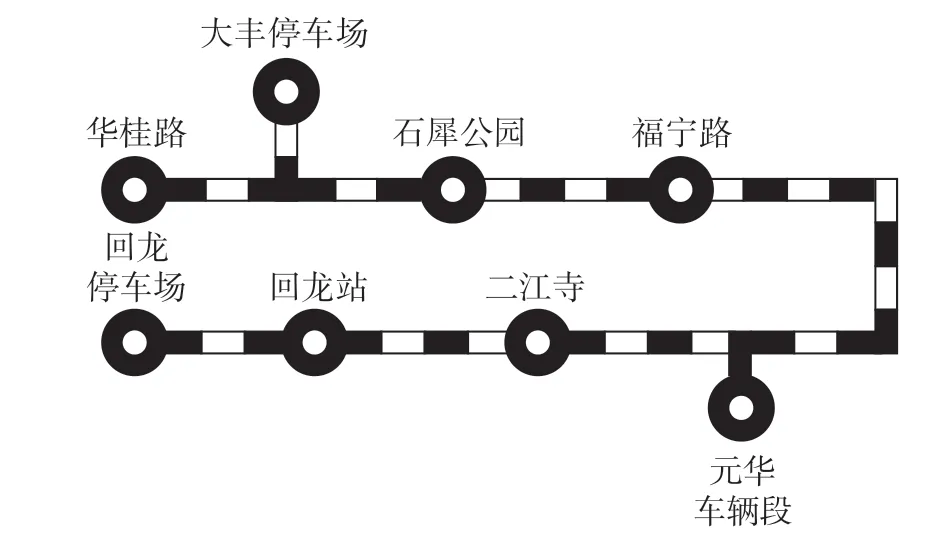
图2 成都5 号线轮乘点设置Fig.2 Schematic diagram of rotation points in Chengdu Metro Line 5

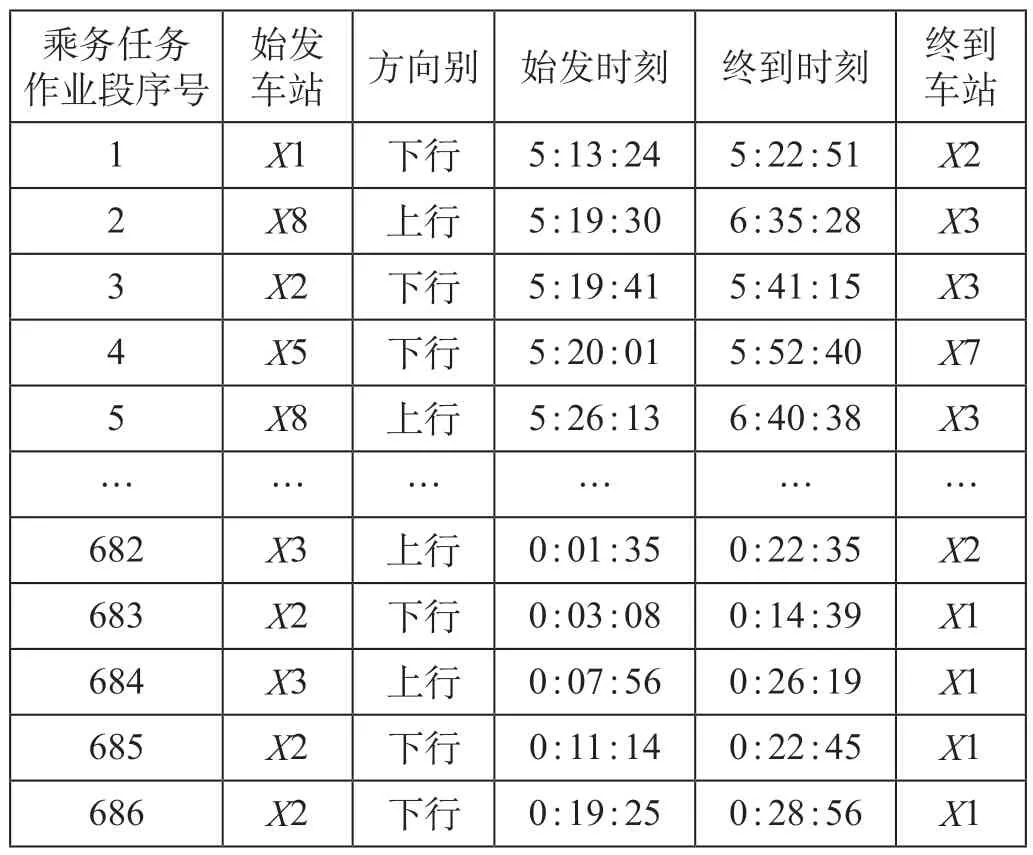
表1 乘务任务作业段数据Tab.1 Data of crew task operation

根据参考文献[1-10]，对已有文献乘务计划编制时涉及的参数范围进行归纳，同时，为进行参数设置分析，需对各参数做出相应的划分，但若将所有可变参数都以1 min 为刻度进行划分，则会导致整个解空间巨大，无法进行有效搜索，为此，根据已有文献归纳的数据并结合工作实际，对各参数作具体划分，现有文献参数范围及划分如表2所示。

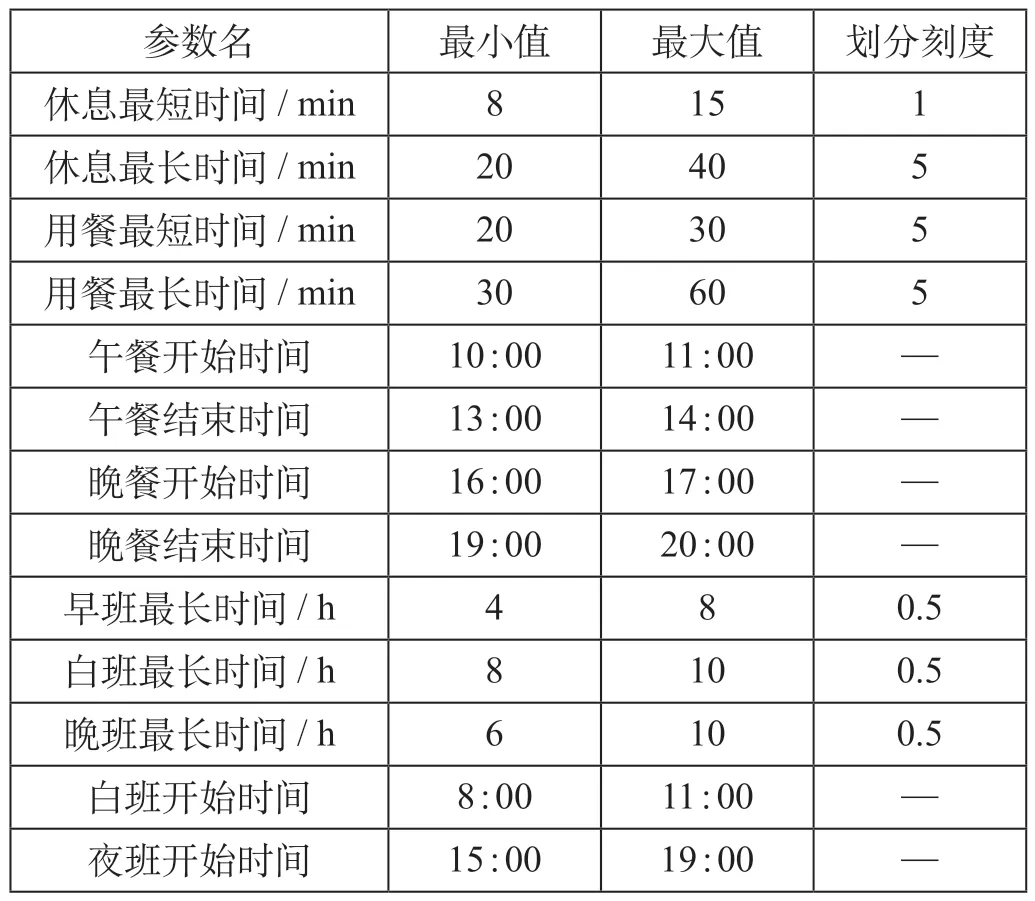
表2 现有文献参数范围及划分Tab.2 Range and division of parameters in existing literature

依据表2 划分的时间跨度，得到各参数节点数，经计算，问题的解空间数量级已经达到10 亿，为此采用软件编程，计算环境是CPU 为Inter (R)Core (TM) i7-10875H 2.30 GHz，内存为16 GB 的DDR4 个人计算机。根据解空间数量，设置迭代次数为100 次，种群数为50，交叉概率为0.6，变异概率为0.01，遗传禁忌搜索算法求解过程如图3所示。

由图3 可知，目标函数值是递增的，求得较优解只需要进行27 次迭代运算，不超过30 次，整体效率为0.836 1，说明设计的遗传禁忌搜索算法在满足参数约束的前提下，能够保证最优解的求解效率，与人工编制乘务排班方案相比，能够有效减少编制时间。

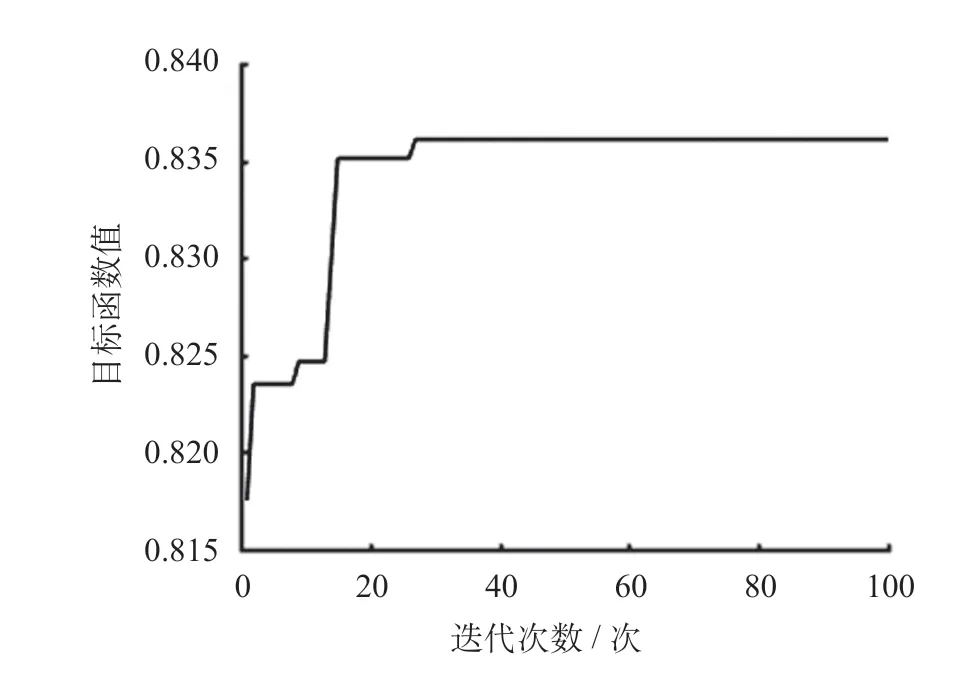
图3 遗传禁忌搜索算法求解过程Fig.3 Solving process of genetic tabu search algorithm

此外，将文献[5]、文献[10]中的参数代入模型中，同时针对两文献中工作时间都是8 h 的情况，引入第3 组参数，改变该组参数中各班次工作时间，求得对应参数下编制的乘务任务效率，不同参数设置下求得的乘务任务表如表3 所示。代入模型求得的最优参数得到排班方案，乘务排班结果如表4 所示。

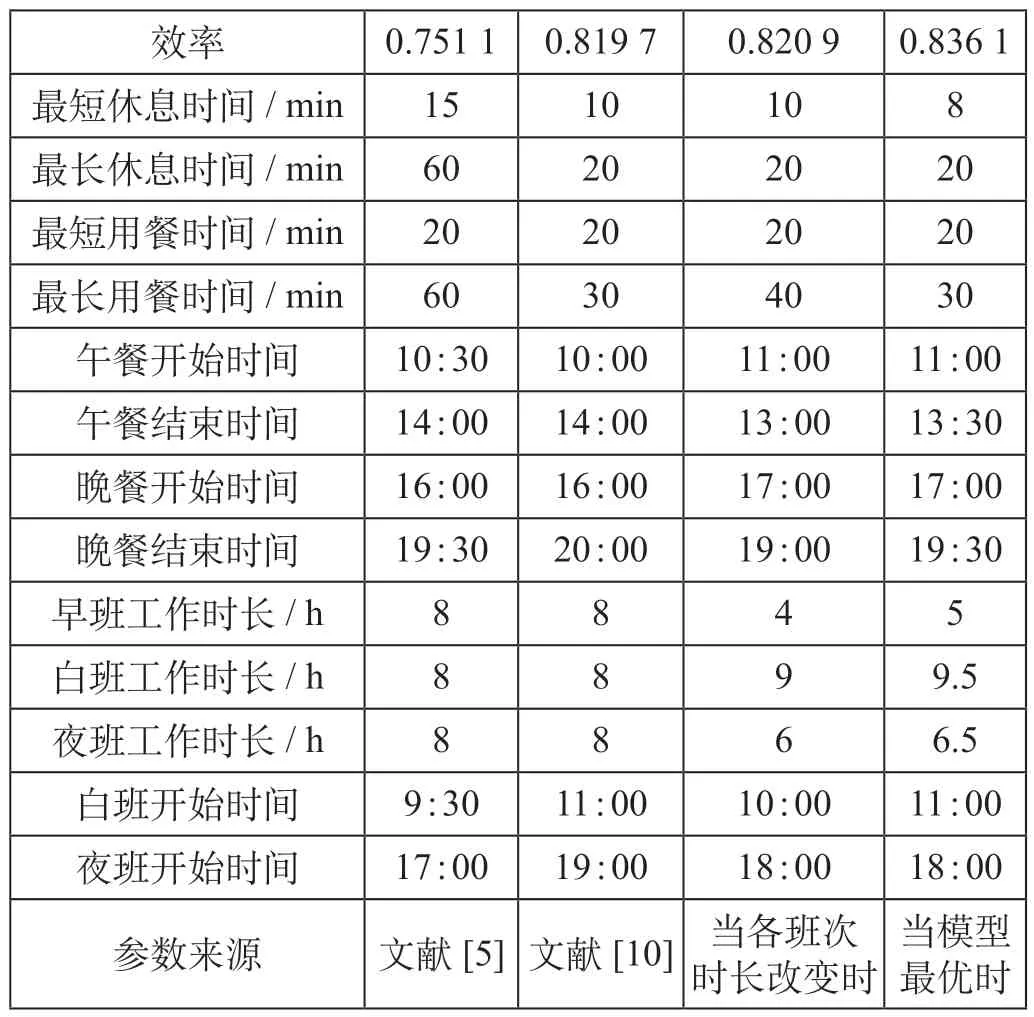
表3 不同参数设置下求得的乘务任务表Tab.3 Crew task table under different parameter settings

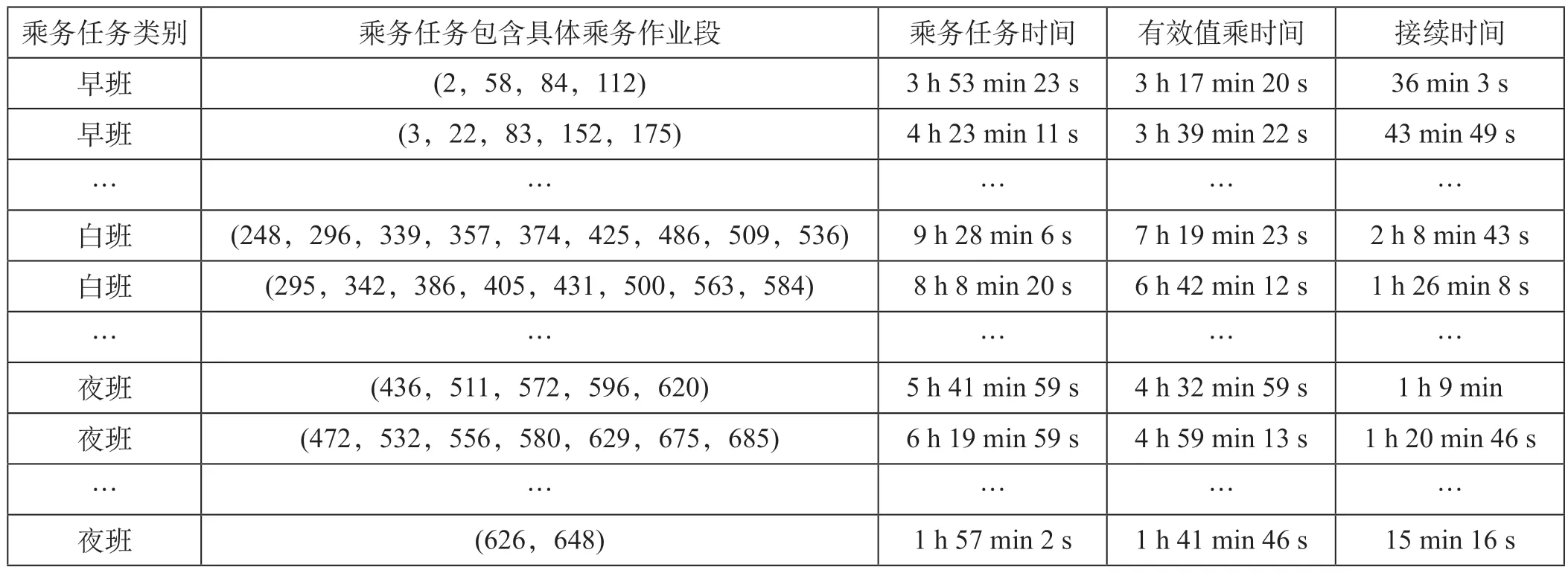
表4 乘务排班结果Tab.4 Crew scheduling results

由表3 可知，所建模型和设计的算法求得的结果明显优于文献[5]、文献[10]中参数所对应的结果，同时文献[5]中各参数求得的效率是最低的，这是因为文献[5]中，乘务作业段间休息最长时间可达60 min，这使得间隔时间跨度较大的乘务作业段也可以进行组合，造成相邻乘务作业段间休息时间过长。

由文献[10]、各班次时长改变组以及本模型求得的最优解可知，各班次工作时长不同也会影响整个乘务任务计划的值乘效率。当各班次最大值乘时间不同时，特别是早班工作时间缩短时，某些原本时间跨度较大的早班乘务任务被提前停止编制，使得原本后续衔接的乘务作业段可以被其余乘务作业段选择，增加了剩余乘务作业段的备选方案，进而提升了整个乘务计划的效率。

由表4 可知，代入最优参数得到的乘务方案中各班次类型工作时长都满足参数要求，方案是可行的。

5 结论

以最大化一日内所有乘务员值乘效率为目标，建立了乘务任务配对模型，并设计启发式算法进行求解，以成都地铁5 号线数据进行验证分析，得到以下结论。

（1）在编制乘务任务时，不同的参数设置会不同程度地影响整个乘务计划的编制，特别是当乘务作业段间的最长休息时间由60 min 变为20 min 时，乘务任务效率显著提升。

（2）与文献[5]、文献[10]中既有参数相比，代入模型求得的最优参数得到的乘务任务能够在满足既有约束前提下有效提高所有乘务员的值乘效率，且设计的算法求解效率和稳定性较高，能够满足实际工作中对排班计划编制的实时性要求。

（3）依据模型设计的遗传禁忌混合搜索算法可以针对实际需求对各时间参数作更为具体细致的划分，进而进行求解，具有很好的适用性。