人口老龄化、生育政策调整与企业年金最优缴费率

曹信邦 张 静

内容提要：本文将延迟退休引入一般均衡世代交叠模型中，考察人口老龄化与生育政策调整背景下企业年金最优缴费率的取值，并分析提高企业年金缴费率的经济效应。测算结果表明，随着人口老龄化程度加深，企业年金最优缴费率会下降；人口增长率提高，企业年金最优缴费率会上升。提高企业年金缴费率能够促进经济增长、提高养老金替代率和企业职工的终身效用水平，但不一定能满足社会福利最大化条件。应根据当前经济目标、宏观经济形势等情况，适当调整企业年金缴费率。

在过去的七十多年时间里，我国经济社会得到了极大的发展。随着社会生产力、生产方式发生变化，中国人口年龄结构也发生了重大转变。人口老龄化是社会发展的必然趋势，我国于2000 年进入老龄化社会以来，老龄化程度不断加深，2020 年我国65 岁及以上人口数为19064 万人，占总人口数的13.50%，伴随而来的包括社会与家庭养老负担加重、产业结构调整受阻与养老市场供求失衡等经济社会问题。积极应对人口老龄化对于加速经济结构转型、促进高质量发展、维护国家人口安全和社会和谐稳定有着重要意义。在应对人口老龄化的改革方案中呼声最高的便是延迟退休政策的出台、生育政策的落实与补充性养老金制度的发展。企业年金作为一种补充性养老金制度，在国民收入再分配及保障城镇职工老年生活方面，发挥着重要的功能性作用。企业年金缴费率是养老保险的重要变量之一，它的取值对职工退休前后的生活质量有着直接影响，因此，本文对不同背景下企业年金最优缴费率的变动进行了分析，为企业年金计划的可持续发展提供政策依据和行动方向。

一、文献综述

目前已有大量研究结果证明延迟退休能有效应对人口老龄化并改善养老金财务可持续性（于文广等，2018；Lacomba 和Lagos，2010；景鹏和郑伟，2020）。同样，众多国内外学者也探讨了生育率对经济的影响，生育率的提高不仅能减轻养老保险财政负担、缓解最优养老基金替代率的下降，还有助于增加未来的资本收益（Blake 等，2006；杨华磊等，2020；司絮，2021）。上述分析论证了延迟退休和鼓励生育政策有助于防范长寿风险，增强养老保险基金的偿付能力。

作为多层次养老保险体系的第二支柱，企业年金发挥着越来越重要的作用。发展企业年金制度有助于保障退休职工的生活质量、完善多层次的养老保险制度，还可以有效缓解我国人口“未富先老”的难题。冯梦骐等（2020）认为在考虑基本养老保险和企业年金的情况下，总养老金财富会随着退休年龄的提高而增加。翟淑萍等（2020）研究发现实施年金计划有助于提高企业的创新水平，并且创新激励效果十分显著。我国企业年金从2006 年正式开始商业化运作，市场也在内生力量与外生力量的推动下日渐成熟和完善，但是与美国、英国等世界主要经济体相比，我国企业年金的发展仍存在较大差距（宣华、赵晨，2016）。同时，我国企业年金在行业、地区和规模等方面也存在不平衡问题。企业年金覆盖面小、基金结余规模相对小、激励政策少和投资管理不够成熟等方面的不足都制约了企业年金的发展(李倩倩等，2019；娄飞鹏，2020）。根据人力资源和社会保障部公布的数据，截至2020 年底，我国制定企业年金计划的公司共有10.5 万个，参加职工人数2717.5 万人，仅占城镇职工基本养老保险覆盖人数的5.95%。因此，有必要采取措施完善和发展企业年金制度，其中非常重要的一项内容就是要确立适当的年金缴费率。

目前研究缴费率的文献大致可分为两类。第一类是基于目标替代率构建精算模型测算企业年金缴费率。翟永会（2014）对不同类型企业和职工所能承担的企业年金最高缴费率进行分析，并根据缴费率精算出所能实现的目标替代率，为发展企业年金制度提出政策建议。张鹏、吴忠（2010）将税收优惠政策与企业年金缴费率结合考察，计算出为了实现目标替代率企业应承担的缴费责任和政府税收优惠力度。

第二类是将缴费率作为未知变量并研究其最优化问题。徐颖等（2012）运用两期世代交叠模型，在最大化个人效用和社会福利的条件下得出不同行业的企业年金最优个人缴费率。景鹏、胡秋明等（2016）以实现社会福利最大化为目标构建一般均衡模型，在考虑延迟退休、生育政策调整的背景下求解稳态最优社会统筹缴费率。于文广等（2021）在OLG 模型中引入了隔代教养和延迟退休等因素，通过内生人口出生率，分析企业年金最优缴费率。通过上述文献回顾可知，OLG 模型被广泛用于对社会养老保险的研究当中，该模型从微观经济主体决策的角度出发，在一般均衡框架内考察养老金对宏观经济的影响，它的优势在于能降低人口异质性特征带来的影响，此外，还能用于探究代际间财富分配机制。因此，本文选择OLG 模型作为研究模型框架。

总之，现有文献中将缴费率作为动态变量的研究不多，对企业年金最优缴费率的关注度也不高。基于此，本文将在OLG 一般均衡模型中，从社会福利最大化角度出发，测算五种生育情景下，不同人口预期寿命的企业年金最优缴费率，从而直接考察人口老龄化和生育政策调整对企业年金最优缴费率的影响，最后分析提高企业年金缴费率的经济效应。

二、一般均衡模型构建

（一）OLG 模型

本文的分析框架以戴蒙德于1965 年提出的两期世代交叠模型为基础，再结合我国实际情况进行具体设定。假定存在三个基本经济单位：个人、企业和政府，并且他们生存在一个封闭的竞争经济中。

1.个人决策

假设经济中所有个体都是同质的，并且只生存成年期和老年期两个时期，每期时间跨度为35年，时间禀赋为1。假设每个个体都能生存到老年期，但在老年期不一定能生存到期满。T表示老年期生存时间（0＜T≤1），基于本文延迟退休的假定，个人在老年期仍需工作一段时间后再退休享受闲暇。Z表示老年期工作时间（0≤Z＜T≤1），代表性个体在成年期的消费和储蓄来自缴纳养老保险后的工资收入，老年期的消费来自成年期的储蓄、缴纳养老保险后的工资收入与养老金收入。个体的效用水平由成年期消费、老年期消费与退休后的闲暇构成，个体以实现自身效用最大化为目标。

1 表示成年人，2 表示老年人。假定个体只在成年期进行储蓄，Wt表示工资水平。b为基本养老保险个人缴纳比例，β 表示个人主观效用贴现因子，φ 表示个人对闲暇的偏好程度，rt+1代表利率水平，St表示储蓄，τ 为总的企业年金缴费率①企业年金所需费用由企业和个人共同承担，参照职业年金中单位与个人的缴纳比例为2∶1，假定企业与个人承担费用的比例也为2∶1，则企业缴费率为，个人缴费率为。（T-Z）Pt+1为老年个体获得的统筹账户养老金，It+1为个人账户养老金，包括基本养老保险个人账户养老金和企业年金个人账户养老金，Gt+1为政府补贴的养老金。求解使个人自身效用最大化的一阶条件可得如下等式：

2.企业决策

假定企业使用的生产要素为劳动和资本，生产出的产品既可用于消费也可用于投资，且由于企业处于完全竞争市场中，产品是同质的。生产函数采用柯布-道格拉斯函数形式，企业的规模报酬不变，则企业在t期的产出为，其中A为外生给定的技术进步，Kt为物质资本投入，Nt为劳动力投入，包括t期的成年个体Lt和t期仍在工作的老年个体ZLt-1，Nt=Lt+ZLt-1。此外，企业还需缴纳税费、基本养老保险与企业年金。假定税费是总产出的一定比重，记为x，并且在本文模型中政府施加的各种税负最终将以某种形式全部转嫁给企业。θ 为基本养老保险企业缴纳费率。企业以实现税后利润最大化为目标，使用资本达到边际产出rt，并且资本在一期完全折旧，雇佣劳动力达到边际报酬Wt。则企业的利润函数为：

企业利润最大化的一阶条件为：

其中kt为单位劳动力拥有的资本存量（下文中，简称劳均资本为劳均产出

3.政府决策

政府的职责在于维持养老保险基金收支平衡，以及确保财政收支平衡。本文假定社会统筹账户养老金采用现收现付制，个人账户养老金采用完全积累制。则t+1 期养老保险基金收支平衡方程如下：

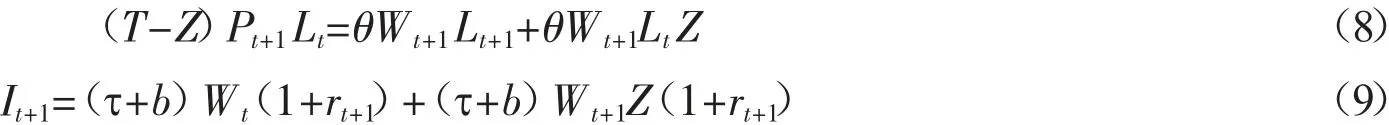
其中，（T-Z）Pt+1Lt是t+1 期企业为职工缴纳的社会统筹账户养老金。It+1为t+1 期退休者的个人账户养老金，bWt（1+rt+1）、bZWt+1（1+rt+1）为基本养老保险个人账户的养老金，τWt（1+rt+1）、τZWt+1（1+rt+1）为企业年金个人账户的养老金。此外，储蓄和个人账户养老金作为经济体系中资本的一部分，其收益率均相同。

假定政府拥有国有资产，国有资产的规模占总资本存量的比重是固定的①该假定参考杨俊、龚六堂和王亚平（2006）论文研究的设定。，设为u，因此政府的财政收支平衡式为：

政府t+1 期的收入来自于国有资产在t+1 期的投资收益、t+1 期收到的税收，收入用于对养老保险制度的补贴支持和公共开支，公共开支占总产出的比重记为g。

根据上述二式可得个体老年期获得的养老金收入，表达式如下：

4.资本市场

每期的资本积累来自上一期的国有资本存量、个人账户养老金和私人储蓄，个人账户养老金既包括成年工作期缴费部分，也包括老年工作期缴费部分。假定资本市场出清，资本积累全部用于下一期的投资，其中ks，t为单位劳动力拥有的国有资本存量。则资本积累的方程是：t+1 期劳均资本表达式如下：

5.模型求解

根据上述所列表达式，推测存在一组变量｛C1，t，C2，t+1，Wt，rt，St，（T-Z）Pt+1，It+1，Gt+1，kt+1｝能满足上述所有假设条件，即达到竞争均衡的动态均衡方程为：

假定经济中存在唯一的、稳定的、非振荡的均衡，这一假定等价于，稳态均衡时，k=t+1kt=k*，则上式可以转化为：

其中u表示国有资本占总资本存量的比重。若对相关参数赋值，即可求出稳态下劳均资本k*，进而得出工资、消费、储蓄和养老金水平。

（二）社会福利模型

首先，将社会福利函数设定为从0 期开始无限存续的个人效用函数的加总，根据个人效用函数表达式，社会福利函数可以表示为：

其中，ρ 为社会效用贴现因子，表示政府对各代人效用的关注度，C2，0表示0 期老年人的消费。

再者，社会福利大小受产品市场出清影响，即企业生产的所有产品需要满足当期所有个体消费与下一期资本积累要求，表达式如下：

最后，将资源约束条件代入构造的以社会福利最大化为目标的拉格朗日函数，得出劳均资本为：

将满足社会福利最大化条件的劳均资本k~代入稳态的动态均衡方程式（15）中，即令k~=k*，此时可得出企业年金最优缴费率τ：

根据上述分析，企业年金最优缴费率受多方面因素共同影响，包括延迟退休的工作时间Z、代表性个体人口预期寿命T、个人主观效用贴现因子β、社会效用贴现因子ρ、人口增长率n①尽管全面三孩政策增强了个人生育自主权，但个人生育子女数量仍然有严格限制，且长期的严格计划生育已彻底改变了社会生育观念，政策实施与否对个体的效用水平影响微弱。因此，本文将n 设为外生变量。、国有资本占总资本存量的比重u、物质资本产出弹性a、基本养老保险企业缴费率θ、个人缴费率b、公共开支占总产出的比重g和税费占总产出的比重x。值得注意的是，该式中不包括综合技术水平A，这是因为当经济达到稳态时，经济增长率等于人口增长率，综合技术进步水平不发挥作用。理论上，相关经济变量对企业年金最优缴费率的影响渠道可根据经济主体的不同分成以下三类：第一，当与个体相关的经济变量发生变动时（如延迟退休工作时间Z、人口预期寿命T、个人主观效用贴现因子β）②人口增长率n 对企业年金缴费率的作用路径不包含个体储蓄水平的调整，当n 变动时，劳均资本随之改变，进而使工资水平发生变动，个体通过对基础养老金的预期改变企业年金缴费率。原因在于本文中人口增长率是外生给定，且个体的效用水平、两期消费与人口增长率也并不直接相关，因此，当n 发生变动时，个体并不会立即调整自身储蓄。，个体首先在成年期调整储蓄分配两期消费以实现效用最大化，储蓄的增减会影响劳均资本水平，进而使工资水平与投资收益率发生变动，基础养老金会随着工资水平的升降而随之增减，由于基础养老金是养老金待遇最重要的组成部分，个体会根据对未来基础养老金的预期改变企业年金缴费率。据此，提出命题1：

命题1：当与个体相关的经济变量发生变动时，个体会先调整自身的储蓄水平，后根据对基础养老金的预期变动企业年金缴费率。

第二，当与企业相关的经济变量发生变动时（如资本产出弹性a），投资收益率会随之改变，为了平滑一生消费，个体会调整自身储蓄，进而改变劳均资本水平，工资水平的变动引致基础养老金的增减，个体会根据对未来基础养老金的预期改变企业年金缴费率。据此，提出命题2：

命题2：当与企业相关的经济变量发生变动时，个体会先调整自身的储蓄水平，后根据对基础养老金的预期变动企业年金缴费率。

第三，当与政府相关的经济变量发生变动时（如社会效用贴现因子ρ、国有股权比例u、税负比重x、公共开支率g），传导路径会根据经济变量是否会直接影响到养老金收入而有所差异。若ρ、u、x发生变动，养老金收入并未受到直接影响，个体不会立即调整储蓄，此时，这三个经济变量或是通过影响劳均资本进而改变工资水平，或是直接影响工资水平，最终使基础养老金增加或减少，个体根据对未来基础养老金的预期改变企业年金缴费率。若g发生变动，意味着政府补贴的养老金变动，未来的养老金收入受到直接影响，个体为了平衡两期消费会调整储蓄，进而改变劳均资本、工资水平和基础养老金，个体会根据对未来基础养老金的预期改变企业年金缴费率。据此，提出命题3：

命题3：当与政府相关的经济变量发生变动时，传导路径会根据经济变量是否会直接影响到养老金收入而有所差异，若经济变量直接影响养老金收入，则个体会根据对养老金收入的预期调整储蓄，反之则反，个体最终根据对未来基础养老金的预期改变企业年金缴费率。

本文将进行参数取值验证提出的命题1、命题2 和命题3。需注意的是，上述分析所隐含的假设是经济处于动态无效状态。这一假定贴合现实，从现有研究来看，学者们普遍认为中国经济处于动态无效状态（袁志刚，2003；黄飞鸣，2010；王松，2013）。且本文中模型参数由现实经济状况设定，根据相关参数取值，可知经济处于动态无效状态。此时，可求解出正的企业年金最优缴费率。

三、参数取值及说明

由上述企业年金最优缴费率的表达式可知，本文涉及的参数有β、ρ、g、x、u、a、θ、b、T、n、Z，在参考已有文献并结合我国实际的情况下，对各参数的设定如下：

（一）贴现参数

1.个人主观效用贴现因子β。现有文献大多将年度时间偏好贴现因子设为0.98 或0.99（景鹏、郑伟2020；王君斌等，2010），本文取0.99，则β=0.9935≈0.7。

2.社会效用贴现因子ρ。社会效用贴现因子反映了政府对各代人效用的关注度，社会效用贴现因子越大，说明政府越重视未来代际的效用水平，本文假设ρ=0.4845①该假设借鉴了于文广等（2021）的假设。。

3.个人对闲暇的偏好程度φ。本文将φ 设为1.5。事实上，个人对闲暇的偏好程度只关系到个人效用水平和社会福利，而不影响最优企业年金缴费率。

（二）经济参数

1.物质资本产出弹性a。根据吴国培（2015）测算的结果，得出2020 年的资本产出弹性为0.425。另外，考虑到我国在十九大报告中提出在2050 年建设社会主义现代化强国的目标，假定至本世纪中叶，我国的资本产出弹性与美国等发达国家相同，其值应为0.3。因此，本文进行折中取值，设定a为0.36 作为研究期间2021-2055 年资本产出弹性的值。

2.综合技术水平A。在基准情形下，本文将其正交化为1。

（三）政策参数

1.基本养老保险企业缴费率θ。2019 年5 月，国家推动养老保险费的降费政策，各地可以将养老保险缴费率由最高20%降低至16%，故将企业缴纳的基本养老保险缴费率θ 设定为16%。

2.基本养老保险个人缴费率b为8%。

3.税费占总产出比重x。根据财政部官网公布的历年财政数据可知，2011-2020 年税收收入占国内生产总值的比重分别为0.1958、0.1937、0.1942、0.1874、0.1846、0.1753、0.1759、0.1701、0.1602、0.1519，该比重大致为逐年递减的趋势。因此本文将x的取值设定为15%。

4.公共开支占总产出的比重g。根据财政部公布的数据可知，2011-2020 年公共预算支出占当年国内生产总值的比重分别为0.2377、0.2421、0.2457、0.2383、0.2597、0.2526、0.2477、0.2403、0.2411、0.2417，总体较为稳定，取过去10 年的平均值0.2447 作为模型中公共开支比重g。

5.国有资本占总资本存量的比重u。本文将国有资本占总资本存量的比重设为0.53②数据来源于裴长洪（2014）的研究结论。。

（四）人口参数

1.人口增长率n。本文以2015 年全国1%人口抽样调查资料数据为基础，将人口按照年龄和性别分成不同的队列，估计出生性别比、人口预期寿命和分孩次生育率来预测中国人口未来总数。

生育情景设计。由于我国在2016 年出台了“全面二孩”政策，因此本文将二孩生育率根据《中国人口和就业统计年鉴》（2017-2020）中的数据进行了调整，此外，为促进人口均衡发展，我国于2021年5 月31 日通过了三孩政策，本文对符合条件且已育有二孩的妇女设计了五种生育情景，然后进行2016-2055 年中国人口情况的预测。即符合条件且已育有二孩的妇女中有0%、20%、50%、80%、100%的妇女愿意生育三孩。由于从政策出台到婴幼儿出生大概需要一年的时间，因此本文从2022年开始调整三孩生育率。

人口预期寿命。根据2015 年全国1%人口抽样调查数据显示，2015 年的男性平均寿命为78.83 岁，女性平均寿命为83.96 岁。按照联合国预期寿命步长法的测算规律，当人口预期寿命达到70 岁后，10 年内寿命增加不会超过1 岁，当人口预期寿命达到80 岁后，10 年内寿命增加不会超过0.5 岁。本文做出积极假设，人口寿命达到70 岁后，每年寿命增加0.1 岁，人口预期寿命达到80 岁后，每年寿命增加0.05 岁。由此可得，至2055 年，男性人口预期寿命为81.83 岁，女性人口预期寿命为85.96 岁。

出生性别比。出生人口性别比是指一定时期内活产男婴数和活产女婴数的比值，按照联合国的设定正常范围是103 至107，2015 年我国人口出生性别比为113.51，假设到2055 年我国人口出生性别比为104，中间年份采用线性插值的方法。

基于上述人口参数的假设，选择CPPS 软件预测三孩政策出台后不同生育情景下中国未来人口总数，统计口径为“城镇人口”，预测时段为2016-2055 年。根据人口预测结果，城镇化率从2016年的56.1%上升到2055 年的80%；在五种生育情景下的人口增长率分别为0.3383、0.3785、0.4385、0.5019、0.5779。

2.老年期生存时间T。由上述分析可知，2055 年男性人口预期寿命为81.83 岁，女性人口预期寿命为85.96 岁，由于到2055 年人口性别比未知，我们假设到2055 年人口预期寿命分别为82 岁、83岁、84 岁、85 岁这四种情况。

3.延迟退休工作时间Z。在本文OLG 模型中一期设定为35 年，并假设个体从20 岁开始参加工作，在55 岁步入老年期。全国“十三五”规划建议提出“出台渐进式延迟退休年龄政策”，尽管具体的延迟退休方案尚未出台，但是目前的大方向是到21 世纪中叶，在现有退休年龄的基础上推迟5-10 年退休。我国目前的退休政策是男性60 周岁，女干部55 周岁，女工人50 周岁。人社部提供的数据显示，我国实际平均退休年龄约为55 岁，因此，本文将基准的退休年龄设为55 岁。假定当前城镇职工的平均退休年龄为55 周岁，将来平均退休年龄为65 岁，则Z=2/7。

表1 参数基准值

四、数值模拟与结果分析

（一）企业年金最优缴费率

通过上述模型推导与参数设定，本文测算了在不同生育方案下，不同预期寿命所对应的企业年金最优缴费率，结果如表2 所示。

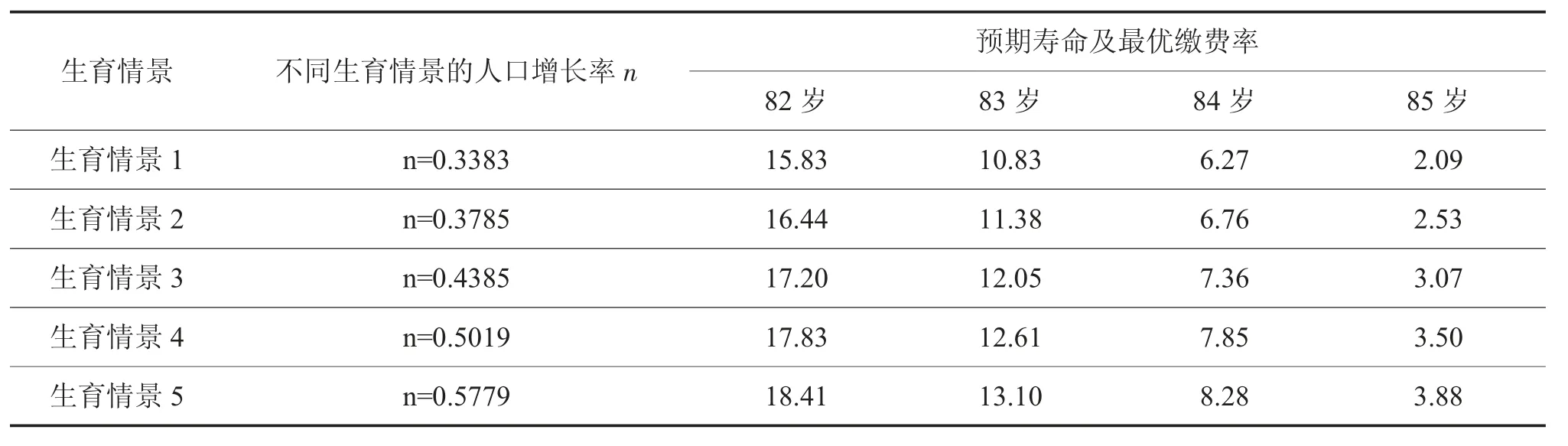
表2 企业年金最优缴费率 单位：%

根据数值模拟结果，企业年金最优缴费率随着人口增长率的上升而上升。可以从以下两个方面解释：一方面，人口增长率上升对企业年金缴费率有正向作用。第一，当其他条件不变的情况下，人口增长率上升会使得劳均资本k 下降，致使工资水平下降，代表性个体为了保障老年期生活质量，会选择增加自己的企业年金，以实现效用最大化。第二，人口增长率上升后政府的开支增加，根据个体获得的养老金收入表达式可以看出，政府补贴的养老金减少，可能需要更高的企业年金缴费率才能使其老年期的收入满足其效用水平。

另一方面，人口增长率上升对企业年金缴费有负向作用。第一，统筹账户养老金表达式显示，人口增长率的上升意味着社会统筹账户缴费人数增多，代表性个体获得的统筹账户养老金增加，因此可能会减少自身的企业年金。然而这一条件能否实现，取决于三孩政策的时滞效应和实施效果，即使是第一批“新生三孩”也需要等到2042 年才能参加工作，企业为其缴纳基本养老保险后效果才能显现。此外，本文考察的时间段为2021-2055 年，所以生育政策调整对企业年金缴费率的影响更为弱化。第二，人口增长率上升导致劳均资本k下降，利率水平上升，使得国有资产、储蓄与个人账户养老金收益率上升，个体可能会在成年期减少储蓄和企业年金水平。通过运算结果看出，在均衡情况下人口增长率上升对企业年金缴费率的积极影响超过了消极影响。因此，人口增长率上升增加了企业年金最优缴费率，即其主要作用路径为n↑→k↓→W↓→τ↑。

人口预期寿命的变动会通过影响个体对储蓄和两期消费的选择进而对企业年金最优缴费率产生影响。从表2 也能看出，随着人口预期寿命的增加，企业年金最优缴费率随之下降。预期寿命延长，处于老年期个体的闲暇时间（T-Z）增加，促使代表性个体增加储蓄以保证老年消费水平，储蓄的增加使得劳均资本也随之上升，工资水平上升，统筹账户养老金增多，企业年金缴费率下降。同时，劳均资本k的上升，会使得投资收益率r下降，则代表性个体为了维持退休后老年人的消费水平，可能会增加企业年金缴费。综合两方面因素可知，预期寿命延长引起企业年金缴费率下降的效应超过了其上升的效应，即为了实现效用最大化，企业年金最优缴费率会随着预期寿命增加而下降，其主要作用路径为T↑→S↑→k↑→W↑→τ↓。

在高预期寿命和低生育率的背景下，降低企业年金缴费率的决定是符合最优化条件的。现实中，我国对企业年金缴费率的规定由2004 年规定的企业和职工个人缴费合计一般不超过本企业上年度职工工资总额的1/6，变化为2018 年企业和职工个人缴费合计不超过本企业职工工资总额的12%。

（二）敏感性分析

当经济系统达到一般均衡状态时，在社会福利最大化的条件下，企业年金最优缴费率的取值也会受到除人口增长率和人口预期寿命之外的其他参数设定的影响。因此，我们对以下基准参数做敏感性分析，即资本产出弹性a、个人效用贴现因子β、社会效用贴现因子ρ、延迟退休工作时间Z、国有股权比例u、税负比重x、公共开支率g。由于在不同预期寿命下各参数变动对企业年金最优缴费率的分析思路相同，仅在影响程度上有所差异，因此我们只对预期寿命为83 岁时五种生育情景下展开分析，结果如表3 所示：

表3 企业年金最优缴费率敏感性分析结果 单位：%

根据表3 分析，a与企业年金最优缴费率呈同向变动。这一结果似乎与现有研究结论相违背，于文广等（2021）认为a越高，意味着老年人的资本回报率越高，则较低的企业年金缴费率就可维持退休后的生活水平。景鹏等（2016）、康传坤等（2014）认为物质资本产出弹性a的提高会降低基本养老保险缴费率。但值得注意的是，上述研究无论从研究重点、研究角度还是研究方法而言，均与本文不同。本文的结论从整个经济系统的一般均衡状态下考察是符合经济学逻辑的。a增大，意味着投资收益回报率上升，个体的储蓄水平存在下降的空间，劳均资本k会随着储蓄水平的下降而下降，进而导致工资水平W下降，这意味着老年期获得的工资收入下降和统筹账户养老金收入下降。为了保证退休后的消费水平，代表性个体增加企业年金缴费，即a↑→r↑→S↓→k↓→W↓→τ↑。β 与企业年金最优缴费率呈反向变动。随着β 的提高，个体将更为重视退休后的消费水平，从而增加储蓄，劳均资本上升，工资水平上升，统筹账户养老金增加，企业年金缴费率进而下降，即β↑→S↑→k↑→W↑→τ↓。ρ 与企业年金最优缴费率的关系为同向变动。ρ 增大，意味着政府更加注重未来各代人的效用，更愿意追求长远利益，根据社会福利最大化条件下的劳均资本表达式可知，当ρ增加时，均衡状态下的劳均资本k下降，进而导致工资水平下降，个体老年期获得的统筹账户养老金收入下降，企业年金最优缴费率上升以保障老年期生活质量，即ρ↑→k↓→W↓→（T-Z）Pt+1↓→τ↑。延迟退休工作期间Z与企业年金最优缴费率呈同向变动。本文认为退休年龄的延长会在增加工作时间的同时减少老年期闲暇时间，从而弱化成年期期的储蓄动机，减少储蓄从而使劳均资本水平下降，企业年金最优缴费率上升，即Z↑→S↓→k↓→W↓→（T-Z）Pt+1↓→τ↑。国有股权比例u与企业年金最优缴费率呈反向变动。随着u的增加，国有资产水平增加，资本存量提高，进一步引起工资水平提高，代表性个体工作期收入增加，由养老金收支平衡式可知，社会统筹账户养老金增加，退休后的财富可以维持其消费水平，引起企业年金缴费率的下降，即u↑→k↑→W↑→（T-Z）Pt+1↑→τ↓。税负比重x与企业年金最优缴费率呈同向变动，由工资水平和投资收益回报率的表达式可知，x的提高意味着工资水平和投资收益回报率的下降，代表性个体预期未来的基础养老金收入下降，将增加企业年金缴费率。即主要影响路径为x↑→W↓、r↓→（T-Z）Pt+1↓→τ↑。公共开支率g与企业年金最优缴费率呈反向变动。随着g的提高，在政府收入一定的情况下，公共开支增加，政府补贴的养老金减少，个体增加储蓄以维持老年期消费水平，劳均资本随之增加，企业年金最优缴费率随之下降，即g↑→Gt+1↓→S↑→k↑→W↑→（T-Z）Pt+1↑→τ↓。

从敏感性分析结果可知，企业年金最优缴费率的确受到资本产出弹性a、个人效用贴现因子β、社会效用贴现因子ρ、延迟退休工作时间Z、国有股权比例u、税负比重x、公共开支率g等因素的影响。因此在决定企业年金最优缴费率τ取值之前，需要充分考虑这些参数取值的合理性，只有设定合理的相关参数，才能获得企业年金最优的缴费率。

数值模拟结果验证了前文提出的命题1、命题2 与命题3，当与微观经济个体相关的变量变动时，个体会先调整储蓄以实现自身效用最大化，在均衡的经济体系中，储蓄的变动会影响其他经济变量，个体最后根据未来的基础养老金选择企业年金最优缴费率。然而，当与政府相关的经济变量发生变动时，由于个体对政策的变动缺乏敏感性，可按照经济变量是否会直接影响养老金收入分情况讨论：若变量可直接影响个体的养老金收入，个体会选择调整自身储蓄，其作用渠道和与微观经济个体相关的经济变量作用渠道类似；若变量无法直接影响个体的养老金收入，个体没有及时调整储蓄，变量通过影响劳均资本、工资水平等，最终影响未来的基础养老金收入，个体根据预期调整企业年金缴费率。这一结论也为我国后续政策的制定提供了参考，即在政策推出时需重点关注个体储蓄的变动情况，进而把握整个经济形势的走向，使政策效果更为精准。

（三）提高企业年金缴费率的经济效应

以上分析是基于社会福利最大化条件并且经济系统达到一般均衡状态时，人口增长率与预期寿命变动下的企业年金最优缴费率测算结果，这提示着我们在社会环境发生变化的背景下制定生育政策时需对企业年金缴费率做出相应的变动，以确保社会福利最大化。假设政府为了提高养老金替代率和促进资本市场发展而决定提高企业年金缴费率，那么这将会给竞争性的经济系统带来什么样的影响？本文将从稳态劳均资本存量、劳均产出、生产要素价格、个人福利这几个角度分析提高企业年金缴费率带来的经济效应，由于不同生育情景和预期寿命下企业年金缴费率对经济变量的影响机制是相同的，因此我们主要分析在预期寿命为83 岁和生育情景3 的情形下，企业年金缴费率从8%上升到20%时经济系统中各变量的变化情况，结果如表4 所示。

观察表4 结果得出，提高企业年金缴费率对经济变量的影响是不同的，从资本与产出的角度来看，提高企业年金缴费率会导致稳态劳均资本k上升、劳均产出y上升。出现这一现象的原因在于代表性个体在工作期缴纳的企业年金是下一期期初资本存量的构成部分，所以提高企业年金缴费率可能会增加劳均资本。但是另一方面，提高企业年金缴费意味着退休期间获得的养老金增加，个体会减少储蓄，即企业年金对储蓄具有一定的“挤出”效应。①当政府提高企业年金缴费率时，由于该变量可以直接影响个体未来的养老金收入，个体选择调整储蓄重新分配两期消费以实现自身效用最大化。这一点从表4 中也可以看出，储蓄同样也是资本存量的一部分，因此提高企业年金缴费率也有存在减少劳均资本的可能。但是最终提升效应强于降低效应，劳均资本增加。从生产要素价格的角度来看，工资水平W下降和资本回报率r下降，工资水平下降的原因在于企业需要承担一部分企业年金缴费责任，因此，企业年金缴费率τ上升，意味着企业的缴费负担加重，最终，劳均资本上升对工资水平带来的增加效应小于企业年金缴费率上升带来的降低效应，工资水平下降。

表4 降低企业年金缴费率的经济效应

从个人福利的角度来看，提高企业年金缴费率降低了储蓄和老年期消费，增加了成年期消费和个体一生的效用水平，个人成年期消费上升源于两种因素共同作用的结果：其一，提高企业年金缴费率会增加老年期获得的养老金收入，则代表性个体的储蓄动机减弱，从而增加成年期消费。其二，提高企业年金缴费率后工资水平下降，成年期收入下降可能会引致消费下降。最终养老金收入上升因素起了决定性作用，成年期消费水平提高。类似地，提高企业年金缴费率对老年期消费影响也存在两个方面，一方面，提高企业年金缴费率后老年期获得的工资水平下降，此外，还会导致资本回报率下降，意味着老年期获得的投资收益率下降，于是会减少老年期消费。另一方面，企业年金缴费率上升会使个体的养老金收入增加，导致老年期消费增加。结果表明，提高企业年金缴费率对老年期消费的抑制效应更大，从而减少了老年期消费。两期消费的变化最终使得一生效用水平增加。

综上所述，提高企业年金缴费率具有积极的经济效应，它不仅促进了经济增长，还提高了个体一生的效用水平。虽然提高企业年金缴费率使得个体工资水平下降和储蓄减少，但是养老金的收入的增加弥补了其对消费的冲击，并提高了个体一生的效用水平。这一结果也为我国发展企业年金、鼓励个体参与企业年金计划提供了理论依据。

五、结论与启示

本文在一般均衡OLG 模型框架内测算了五种生育情景下不同预期寿命下企业年金的最优缴费率，并分析提高企业年金缴费率对各经济变量的影响。测算结果表明：首先，企业年金最优缴费率随着人口预期寿命的上升而下降，随着人口增长率的上升而上升。在相关参数的合理设定下，0%-100%符合政策条件且已育有二孩的妇女生育三孩时，预期寿命为83 岁的企业年金最优缴费率变动范围为10.83%-13.10%，预期寿命为84 岁的企业年金最优缴费率变动范围为6.27%-8.28%。企业年金最优缴费率随着人口增长率的上升而增加的结论是根据经济一般均衡状态所得出的，与养老金制度一般感性认识不同。其次，企业年金最优缴费率不仅受到人口预期寿命与人口增长率的影响，而且还有赖于资本产出弹性、个人效用贴现因子、社会效用贴现因子、延迟退休工作时间、国有股权比例、税负比重、公共开支率等参数的合理设定。最后，提高企业年金缴费率增加了劳均资本存量、劳均产出、成年期消费、养老金收入、一生效用水平。但是，提高企业年金缴费率减少了资本回报率、工资水平和私人储蓄。

因此，本文提出如下政策建议。（1）尽快制定延迟退休方案与政策。在当前人口老龄化背景下，养老保障负担加重、劳动力总量萎缩和劳动力年龄结构老化等问题接踵而至，而这些并不利于经济的健康发展，实施延迟退休政策有利于进一步开发老职工人力资源的价值、增加个体获得的养老金收入并维持养老金收支平衡。（2）实施与全面三孩政策配套的生育支持政策。第七次人口普查数据显示，2020 年我国育龄妇女总和生育率仅为1.3，而根据国家统计局的有关调查，我国育龄妇女的生育意愿子女数为1.8，这提示我们必须做好相应的生育支持政策才能释放出实际存在的生育潜力，配套措施包括发展普惠托育服务体系、鼓励隔代教养、延长育儿假等。完善生育支持政策提高生育率以促进人口长期均衡发展，增加社会福利、保持我国人力资源禀赋优势。（3）加大企业年金宣传力度、完善税收优惠政策。激励更多的企业参与企业年金计划，提高企业年金基数水平，发挥企业年金作为补充性养老金制度的作用，完善多层次养老保障体系。同时要根据宏观经济形势、养老保险基金收入情况、企业成本等因素，适当调整企业年金缴费率。提高企业年金缴费率能够促进经济增长、提高养老保险替代率和企业职工的终身效用水平，但不一定能满足社会福利最大化条件。因此，在针对不同情况时，我们应充分权衡各方面利弊后再进行相应调整。同时，本文也有一些不足之处：就参数设定而言，本文存在一定的主观性，如a、β 的取值等。其次，本文探讨了稳态的企业年金最优缴费率，而缺少对不同人口预期寿命和不同生育情景下经济变量动态变化路径的考察，这也是在后续研究中待解决的问题。