基于半导体激光器窄线宽光子微波信号获取

蒋再富，张定梅

(荆楚理工学院 数理学院，荆门 448000)

引 言

由于微波在无线通信网络、雷达、传感器和卫星通信中具有广泛的应用前景，它的产生、处理以及分发一直备受关注。与传统电子方法相比，光学方法产生的微波信号具有宽的带宽、连续可调的微波频率和能直接光纤传输等优点[1-6]。目前光子微波信号的产生可分为直接调制、外部调制、光学外差法、锁模、光电振荡和单周期(period one，P1)振荡法。其中，P1动力学可产生于外光注入下的半导体激光器(semiconductor laser, SL)，其产生机制是当注入强度和频率失谐选择合适的值时，在SL内可生成两个重要频率成分，一个是激光器的腔共振频率，另一个是注入引起的再生频率成分，这两个频率成分拍频后可产生P1振荡[1]。相比于其它的技术，P1动力学具有单边带的光谱结构、低成本、全光设备配置和宽频率调节范围等优点[7-11]。

然而，由于SL中固有的自发辐射噪声的存在，会使产生的光子微波信号具有较大的线宽，这将影响P1微波信号的实际应用[12-14]。因此，如何降低P1微波线宽是一个亟待解决的问题。目前，关于P1微波线宽窄化的研究已经有一些报道[15-20]。例如，JI和XUE等人在一个光注入下的垂直腔面发射激光器中引入了两个光反馈环路来降低产生的P1微波信号的线宽，通过恰当调节两个环的反馈参量，微波线宽至少能降低两个数量级[16-17]。SIMPSON等人在一个光注入下的分布式反馈(distributed feedback，DFB)激光器中引入了极化旋转光反馈来稳定微波信号，研究表明，与直接光注入下测得的线宽相比，引入光反馈后微波信号的线宽被窄化了至少两个数量级[18]。LO等人研究了超短腔光反馈对光注下DFB激光器产生的P1微波信号线宽的影响，发现引入光反馈后光子微波的线宽能降低3个数量级[19]。ZHUANG等人在一个光注入下的DFB激光器引入双光反馈来压缩微波线宽，发现通过优化反馈参量，微波线宽能从8.2MHz压缩至50kHz[20]。因此，引入光反馈是压缩P1微波线宽的一种有效方式。

光纤布喇格光栅(fiber Bragg grating，FBG)是光纤传感器、光纤通信、光信息处理中重要的无源器件，其光栅周期沿轴向均匀分布并且折射率为常数。相关研究表明，在SL中引入FBG光反馈可产生宽带宽的混沌信号，并能有效消除混沌信号的时延特征[21]。但是，关于引入FBG光反馈来降低微波线宽的研究却未见报道。FBG中的分布式反馈光栅能过滤掉反馈光中的一部分频率成分，这将有利于P1动力学的自我锁定，进而降低线宽。本文中将理论研究FBG光反馈对光注入下DFB-SL产生的P1微波信号线宽的影响。通过研究注入系数对微波频率和微波强度的影响来选择合适的注入参量，并引入FBG光反馈来压缩微波线宽，讨论反馈强度和反馈延迟时间对微波线宽的影响。

1 数值模型及描述

图1是利用半导体激光器产生窄线宽光子微波信号的示意图。其中,可调激光器(tunable laser，TL)的输出光经过分束器(beam splitter，BS)BS1后注入到SL中，使SL进入P1振荡。SL输出的光经过分束器BS2分成两部分，一部分光经FBG反馈后再回到SL来压缩线宽，一部分光输出后被探测。透镜L1和L2分别为准直和汇聚透镜。基于SL的Lang-Kobayashi模型并引入FBG光反馈后，描述基于SL的窄线宽光子微波信号产生的速率方程为[21]：

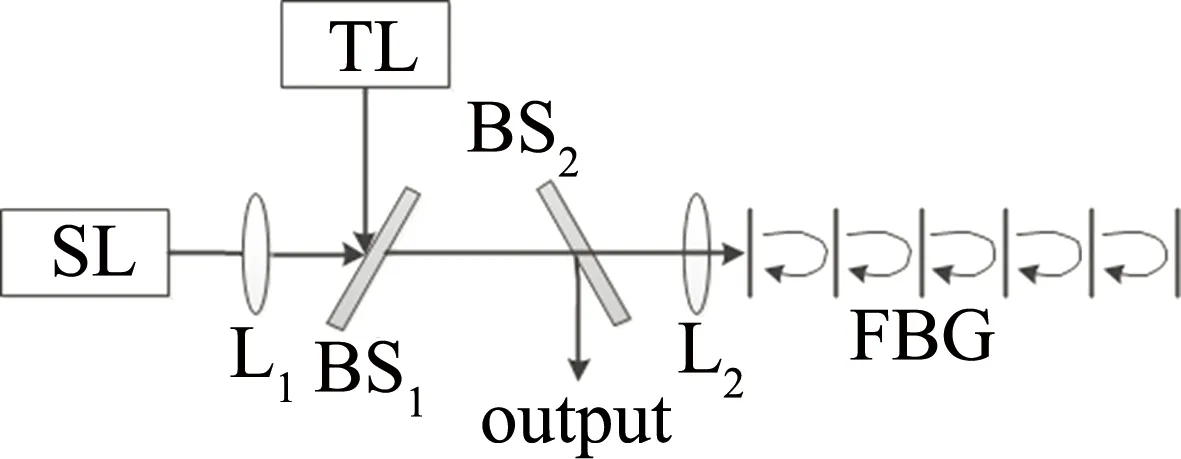
Fig.1 Schematic diagram of narrow linewidth photonic microwave signal generation

ξγa0exp(-i2πΔνt)+ηγexp(iθ)[r(t)×

exp(-iΔΩt)]*a(t-τ)+F

(1)

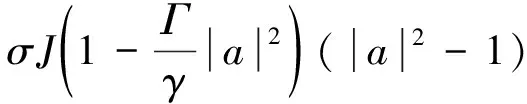
(2)

r(Ω)=

(3)

式中，a为电场复振幅，n为载流子数，a0为激光器自由运行时的电场强度，η为滤波反馈强度，τ为外腔反馈时间，Ω表示角频率，ΔΩ为激光器频率与FBG中心频率的角频率失谐，θ为相位变化，ξ为注入强度，Δν为注入频率失谐，γ为腔衰减速率，σ为自发载流子弛豫速率，ρ代表微分载流子弛豫速率，Γ代表非线性载流子弛豫速率，b是线宽增强因子，J为归一化的电流，κ为FBG的耦合系数，L为FBG腔长，r(t)为FBG在时域中的响应，r(Ω)为FBG在频域中的响应，δ=NΩ/c表示反向传播模式与FBG布喇格频率的相位失配，N代表光纤折射率，c表示光速。FBG的带宽可由κc/(πN)得出，F为噪声项，“*”表示卷积运算。参量的物理含义和取值请见表1。

Table 1 Simulation parameters of the laser and FBG

值得一提的是，在上述速率方程推导的过程中，TL和SL使用的复电场ETL(t)和ESL(t)分别为：

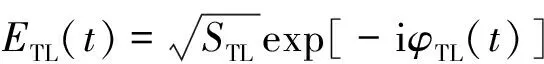
(4)

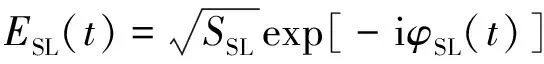
(5)

式中，STL和SSL分别表示TL和SL输出的光子数，φTL(t)和φSL(t)分别表示TL和SL的相位,φTL(t)和φSL(t)是与时间相关的函数，由于TL工作在稳定态，所以假设它的相位φTL(t)为常数0。尽管在TL的注入下，SL的相位φSL(t)随时间波动，但是它的波动较小，因此也假设为一常数。在这样的假设下两束激光的相位差在仿真过程中是保持恒定的[22]。

为了量化微波线宽，文中使用常用的微波频率随微波功率分布的标准方差进行计算，具体的表达式为：

Δf=[〈ν2〉-〈ν〉2]1/2

(6)

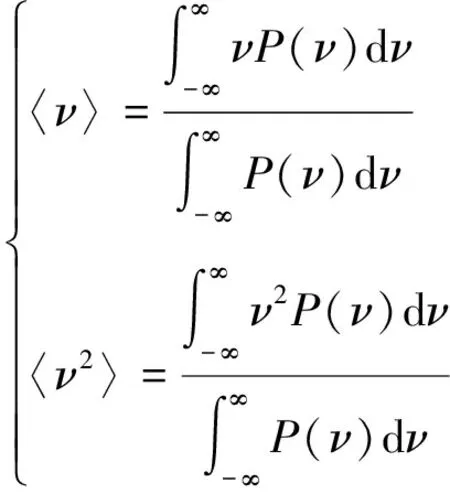
(7)

式中，Δf表示光子微波的线宽，ν和P(ν)表示功率谱中的频率和相应的功率。

2 结果及讨论

2.1 光注入下SL的动力学

图2是半导体激光器(SL)在外部光注入下的分岔图。图中的点代表了Δν=8GHz时不同的反馈强度下SL输出的时间序列的极值。如图2所示，当ξ从0增加到0.012时，SL输出的时间序列有两个极值，表明此时SL工作在单周期(P1)振荡态[7]；当ξ从0.012增加到0.038时，输出的时间序列有4个极值，说明SL输出的动力学态为倍周期态；当ξ位于0.038～0.058之间时，时间序列的极值增多并具有遍历性，说明此时SL工作在混沌态；继续增加ξ，SL将输出单周期态和注入锁定态。因此，外部光注入SL会产生丰富的非线性动力学行为。接下来将研究利用P1态来产生光子微波信号的性能。

Fig.2 Bifurcation diagram of the SL for Δν=8GHz

2.2 微波频率和微波强度分布

首先研究仅在光注入下的SL产生的光子微波信号的性能，图3中给出了频率失谐Δν=10GHz，ξ=0.14时SL输出的时间序列、光谱和功率谱,此时未引入FBG光反馈。如图3a所示，时间序列呈现出峰值相等的规则振荡，说明此时SL工作在P1振荡态。图3b中给出了相应的光谱，其中，fc为激光器的腔共振频率，fi为注入光在SL中的再生光学成分。fc和fi拍频后形成了光子微波的基础频率。值得注意的是，fc并不在光谱的零频率处，这是由于光注入引起的腔共振频率红移效应造成的。图3c中给出了相应的频谱，f0为基础微波频率，是光谱中腔共振信号和注入再生信号拍频的结果，其值为20.1GHz，后面的峰值为高次谐波。另外，从功率谱中可以看出，此时的微波强度为-66.7dB。光注入SL产生P1振荡的物理实质是:外部的注入光会与腔内的载流子产生相互作用，进而在SL的腔内产生与外部光频率对应的再生光学信号，这个信号的强弱与注入光的强度有关。由于SL腔内自身存在振荡的光学成分，当注入参量选择合适时，腔内光学成分和再生光学成分会共存。而在频谱中观察到了P1振荡就是这两个光拍频的结果。相似的物理现象已经在实验中被观察到[18]。

Fig.3 Time series, optical spectra, and power spectra of the SL for Δν=10GHz and ξ=0.14

为了全面掌握微波频率f0和微波强度P0随注入参量的变化规律，图4中展示了f0和P0在注入强度ξ和频率失谐Δν构成的参量空间中的分布情况。在这里，Δν的变化范围是0GHz～50GHz，ξ的变化范围是0～0.5，图中白色部分代表了除P1以外其它的动力学态，黑色线标出了频率分布的等高线。从图4a中的等高线也可以看出，对于相对较小的频率失谐值，随着注入强度的增加，微波频率逐渐增加，这是由于逐渐增加的注入强度加剧了腔共振红移效应。但是对于较大的频率失谐值，随着频率失谐量的增加，微波频率将逐渐变得对注入强度不敏感。这是由于较大的频率失谐下，红移效应逐渐减弱造成的。图4b中给出了对应的微波强度P0分布，对于某一个固定的频率失谐值，微波强度先是随着注入强度的增加逐渐增加，到达最大值之后在Hopf分岔边界处逐渐减小。这是由于在靠近Hopf分岔处，系统即将由P1动力学进入其它动力学态，这将毁坏P1动力学的稳定性，进而降低了微波强度。在下面的讨论中，注入系数被选择在最大微波强度处。

Fig.4 Distributions of the microwave frequency f0 and microwave intensity P0 in the parameter space

2.3 微波线宽窄化

在引入FBG滤波光反馈之前，必须掌握FBG的相关物理特性，FBG的频率响应函数如(3)式所示，但是频率响应函数是在频域中进行计算的，而SL的方程是关于时间的常微分方程，因此，必须把频率响应函数作逆向傅里叶变换变化到时域中进行计算。图5中给出了计算出的FBG反射谱。图中纵坐标为反射率，横坐标为相对于FBG中心频率的频率失谐。此时主瓣的半峰全宽(full width at half maximum,FWHM)fFWHM=13.2GHz，旁瓣的重复频率为fl=4.4GHz。从图5中可以看出，在靠近主瓣中心的地方反射率近似等于1，远离主瓣中心后反射率迅速下降。因此，外部光进入FBG后会滤掉一部分频率成分。

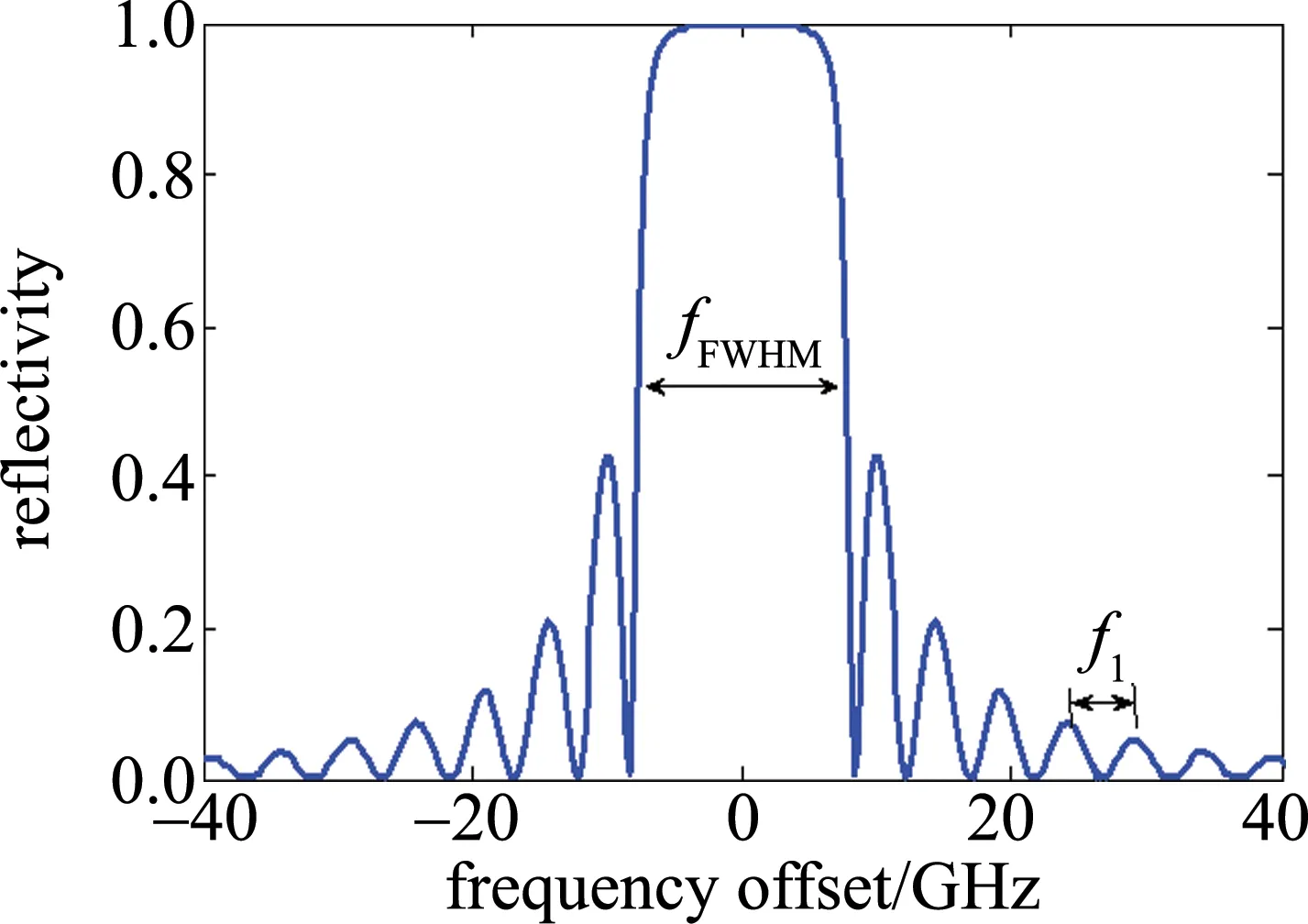
Fig.5 FBG reflection spectrum

图6中给出不同参量下未引入FBG光反馈(第1行)和引入FBG光反馈(第2行)后SL激光器输出的功率谱。当(Δν,ξ,η,ΔΩ)=(10.0GHz,0.14,0.17,10GHz)时，如图6a和图6d所示，在未引入FBG光反馈前，微波频率f0=20.1GHz，微波的线宽Δf=17.1MHz，线宽较宽。此时微波信号质量不高的原因是由于在仿真过程中加入了较强的高斯白噪声。较大的噪声将会使激光器腔内载流子数波动加剧，进而会提高输出光的相位噪声，最后使微波信号的线宽加宽，质量变差。引入FBG光反馈后，微波线宽被压缩到了2.6kHz，线宽被明显压窄。其线宽窄化的物理机制是P1动力学的自我锁定。具体而言，SL输出的P1微波信号进入FBG中进行滤波，选择合适的滤波频率失谐后，FBG将过滤掉与P1微波频率无关的频率成分，最后将这个经过频率选择后的信号输入到SL中，使SL中的P1振荡实现了自锁定，相位噪声降低，线宽明显变窄。同时也注意到，引入FBG光反馈后，微波频率增加到了23.8GHz，这是由于光反馈的作用下导致的激光腔共振频率红移造成的。此外，引入光反馈后，在微波频率的两边出现了边带，这是光反馈引起的外腔模[20]。当(Δν,ξ,η,ΔΩ)=(20.0GHz,0.2,0.17,20GHz)时，如图6b和图6e所示，未引入光反馈前，微波线宽为30.8MHz，引入光反馈后微波线宽被压缩到5.2kHz。当(Δν,ξ,η,ΔΩ)=(30.0GHz,0.28,0.19,30GHz)时，如图6c和图6f所示，仅在光注下的线宽为50.2MHz，引入光反馈后，微波线宽被压缩到了3.4kHz。因此，通过合适选择反馈参量，微波线宽能够被至少压缩3个数量级。说明FBG光反馈能有效压缩微波信号的线宽，改善微波信号质量。

Fig.6 Power spectra of different microwave frequencies

图7中展示了不同频率失谐下微波线宽随反馈强度的变化。图中注入强度选择为最大微波强度处，反馈延迟时间固定为2ns，纵坐标为对数坐标。当参量(Δν,ξ,ΔΩ)=(10GHz,0.14,10GHz)时，如图中圆圈所示，在未引入光反馈的情况下微波线宽为17.1MHz，线宽较宽。引入光反馈后，当反馈强度由0逐渐增加到0.05时，线宽逐渐变小，这是由逐渐增加的自注入锁定效应引起的，进一步增加反馈强度到0.2，线宽继续下降并伴随着剧烈抖动，当η=0.17时，线宽取最小值为2.6kHz；当(Δν,ξ,ΔΩ)=(20GHz,0.17,20GHz)和(30GHz,0.28,30GHz)时，如图中的圆圈和三角所示，线宽的变化趋势与Δν=10GHz时相同，当η分别等于0.17和0.19时，线宽分最小值为5.2kHz和3.4kHz。从图7中可以看出，在各种频率失谐下，FBG光反馈均能有效压缩微波线宽。

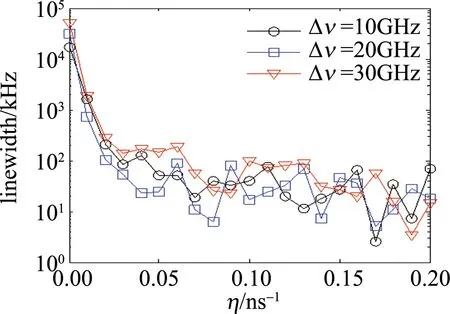
Fig.7 Microwave linewidth as a function of feedback intensity under diffe-rent frequency detuning

3 结 论

数值研究了FBG滤波光反馈对光注入半导体激光器(SL)产生的光子微波信号的线宽的影响。首先讨论了注入参量对微波频率和微波强度的影响，发现当固定频率失谐时，微波频率随着注入强度的增加逐渐增加，微波强度随着注入强度先增加再逐渐减小。微波频率具有较大的调节范围，通过调节注入强度可以优化微波强度。此外，通过计算发现,由光注入产生的微波信号的线宽较宽，所以引入FBG滤波光反馈来压缩微波线宽。研究发现，当反馈时间固定时，微波线宽随着反馈强度的增加逐渐减小，并且通过优化反馈强度，微波线宽能够至少降低3个数量级。本研究为基于SL的窄线宽的光子微波信号的获取提供了一定的理论支持。