脉宽对激光撞击电子辐射峰值影响的模拟计算

王浩冉，夏福源，田友伟

(1.南京邮电大学 贝尔英才学院，南京 210023；2.南京邮电大学 理学院，南京 210023)

引 言

由于激光的高方向性、高相干性等特点，激光的运用范围日益广泛，这也激起了学者对于激光与物质作用领域的兴趣。激光脉冲与电子的作用关系也成为研究热点之一。20世纪中期出现了锁模技术[1-3]与激光调Q技术[4-5]，分别通过对激光进行共振调制以及压缩振荡脉冲宽度的方法实现了对激光脉宽的缩短，达到了fs量级，与此同时也进一步使激光的强度不断增大[6]，逐渐逼近1015W量级。

20世纪80年代，MOUROU等人发明了啁啾脉冲放大(chirped pulse amplification，CPA)技术[7]，这种方法使除主脉冲之外的噪声得到了很好的抑制，其方法是先放大激光前分散种子脉冲的能量，再压缩处理，激光场强度的发展因而实现了质的飞跃，突破至1020W量级。

目前，人们已经可以通过啁啾脉冲放大技术获取超高聚焦强度的飞秒激光脉冲。此时高能激光场中受到正交于运动方向的洛伦兹力的电子会产生同步辐射[8-10]，这种电子拥有小型化、高亮度、稳定且具有潜在应用等特点[11-13]，因而通过激光脉冲加速做相对论加速的电子放出的同步辐射现象已经开始被广泛研究[14-17]。但有关激光脉宽对电子电磁辐射影响方面的研究还不足，迫切需要一种分析激光脉宽对电子电磁辐射方面影响的方案，来预测电子的辐射功率峰值以及分布情况。通过改变激光脉宽来研究激光脉冲撞击电子所产生的电子汤姆逊散射特性对于研究电子的同步辐射提供了一定了理论基础，具有重要意义。

作者以Lorentz方程以及电子辐射方程为基础建立了紧聚焦激光作用于静止单电子模型，同时运用了MATLAB软件模拟了不同激光脉宽的椭圆偏振光与电子相互作用时电子汤姆逊散射所产生的电磁辐射的分布情况,并详细讨论了电子辐射功率峰值及其时间函数、频谱特性与激光脉宽的关系。

1 紧聚焦激光撞击单电子辐射模型

1.1 椭圆偏振紧聚焦高斯脉冲矢量势

椭圆偏振紧聚焦激光脉冲在3维坐标系中的相位可表示为[18]：

φ=η+c0η2+φR-φG+φ0

(1)

式中，c0是激光脉冲的啁啾参数；φ0为初始相位;η=z-t，z为电子在z轴的坐标，t为观察点的时间;φR=(x2+y2)/[2R(z)]是与激光脉冲在轴处的波阵面曲率半径R(z)=z(1+zR2/z2)有关的相位，而φG=z/zR则是与高斯光束从-∞传到+∞时将经历π位相变化相关的古依位相，其中zR=w02/2为激光脉冲的瑞利长度，而w0为激光脉冲的最小半径。

下式常被用于表示紧聚焦高斯脉冲激光电场的归一化矢势[18]：

a(η)=a0exp(-η2/L2-ρ2/w2)(w0/w)·

[cosφ·x+δsinφ·y]

(2)

式中,a0是被mc2/e归一化的激光振幅，电子的静止质量和电量则分别由m和e表示，其数值分别为9.1×10-31kg和1.6×10-19C;ρ2=x2+y2;L是激光的脉宽;w0是激光脉冲的最小半径，w是激光脉冲的束腰半径，且满足w0=w/(1+z2/zR2)1/2;文中取偏振参量δ=0.9表示激光为椭圆偏振;x，y分别表示x，y方向单位向量。

1.2 电子的辐射方程

如图1所示，椭圆偏振激光沿着+z传播，撞击处于原点的静止电子，由于激光脉冲具有质动力，电子会随着撞击方向移动[19]，同时散发出谐波辐射，n为辐射方向，且有：

n=sinθcosφ·x+sinθsinφ·y+cosθ·z

(3)

式中，φ和θ分别是图1中所示的观测方位角和极角。

用洛伦兹方程来描述电子在电磁场中的运动[18]：

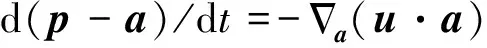
(4)

同时有电子的能量方程为[18]：

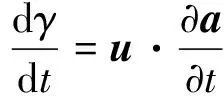
(5)

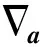
做相对论加速运动的电子会释放电磁辐射[20]，辐射的单位立体角的功率计算公式为：

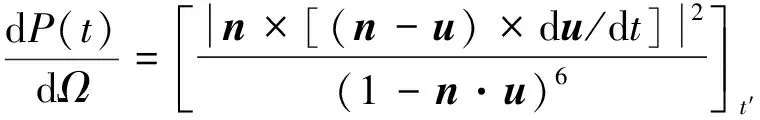
(6)

式中,辐射功率P(t)已被e2ω02/(4πc)归一化,ω0为激光频率，Ω为单位立体角，t′是电子的延迟时间。t′和t之间存在如下关系[20]：

t=t′+R0-n·r

(7)

式中,R0为观测点与电子的距离,r为电子位矢。此处假定观测点远离激光与电子的作用点。

单位立体角单位频率间隔内辐射强度为[20]:

(8)

式中,I为辐射强度，ω为辐射频率，d2I/dωdΩ被e2/(4π2c)归一化,s=ωs，b/ω0,ωs，b为散射所产生辐射的频率，电子谐波辐射的时间以及频谱特性可以通过求解(8)式得到。

2 数值模拟结果

运用MATALB进行不断迭代计算，模拟了椭圆偏振紧聚焦的飞秒激光与静止电子相互作用的过程，并通过改变激光脉宽的方式得到的汤姆逊散射辐射功率分布图,如图2所示。电子初始状态为静止，入射光是偏振参量δ=0.9的椭圆偏振，入射激光强度a0=3W/cm2，激光脉冲最小半径w0=3λ0,相对论因子γ0=1,光脉宽分别为λ0,2λ0,3λ0。

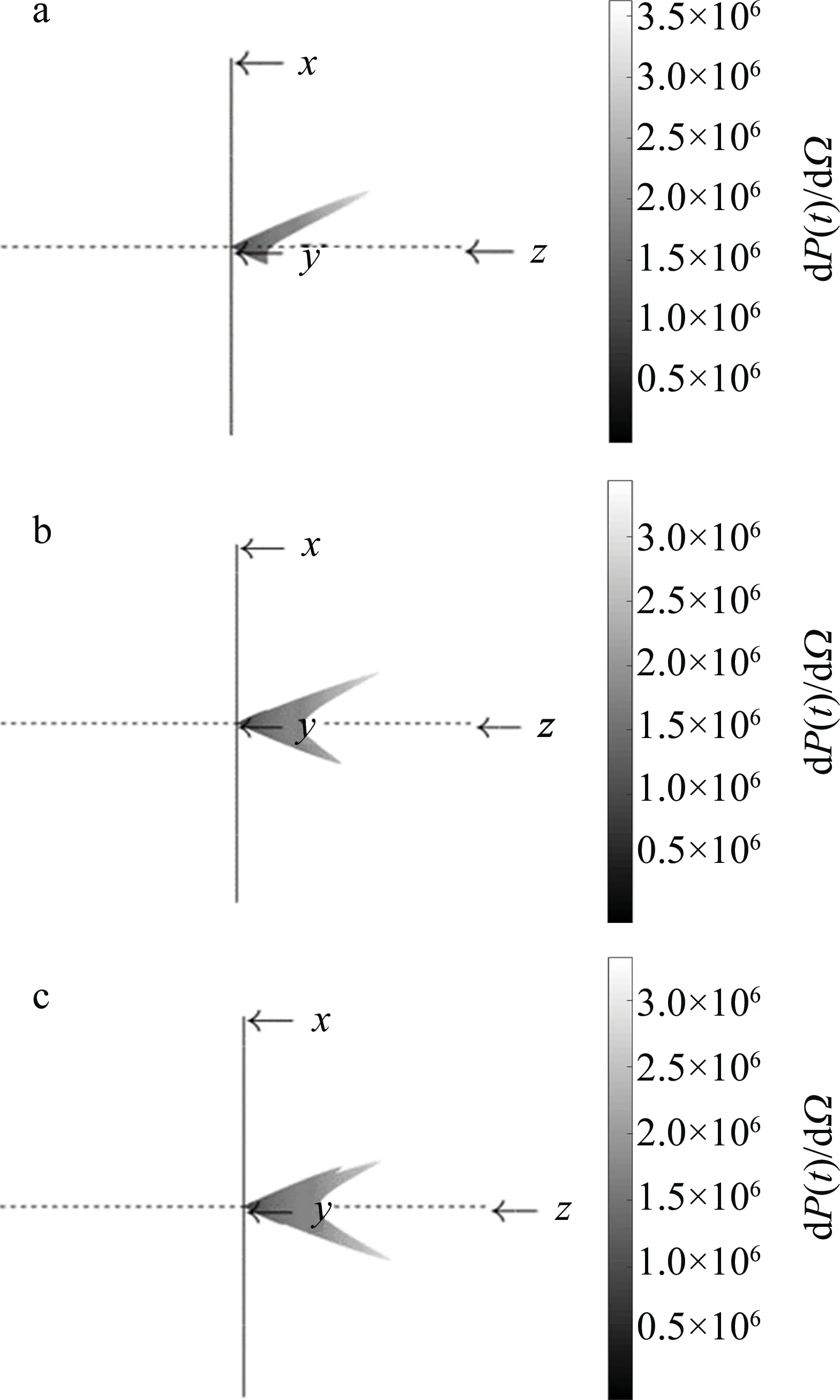
Fig.2 Influence of different laser pulse width on power distribution of electron Thomson scattering radiation

电子辐射集中在一个电子运动方向上的窄圆锥体内，如图2a～图2c所示，这是由于当粒子获得超相对论性能量时，发射的辐射类型接近同步加速器，发出同步辐射，即沿着运动的切线方向发出辐射。而辐射功率呈现出双峰的趋势，这是因为受到激光作用时，电子沿着曲线运动并沿脉冲传播方向飘移，每周期通过速度为零的点两次[21-22]，此时粒子的辐射功率达到峰值，即一个周期中有两个辐射功率峰值点。

如图3所示，激光偏振参量、入射激光强度、束腰半径、相对论因子等参数同图2，激光撞击单电子模型中，激光脉宽的增大使得电子谐波辐射不断增强，也使电子的辐射峰值功率双峰现象逐渐明显(如图3a～图3c所示)，这是因为入射激光脉宽的增加，使电子辐射脉冲的个数相应增加，进而引起了辐射能量功率的增加。但是电子的辐射峰值功率随着激光脉宽的增大呈现出下降的趋势。

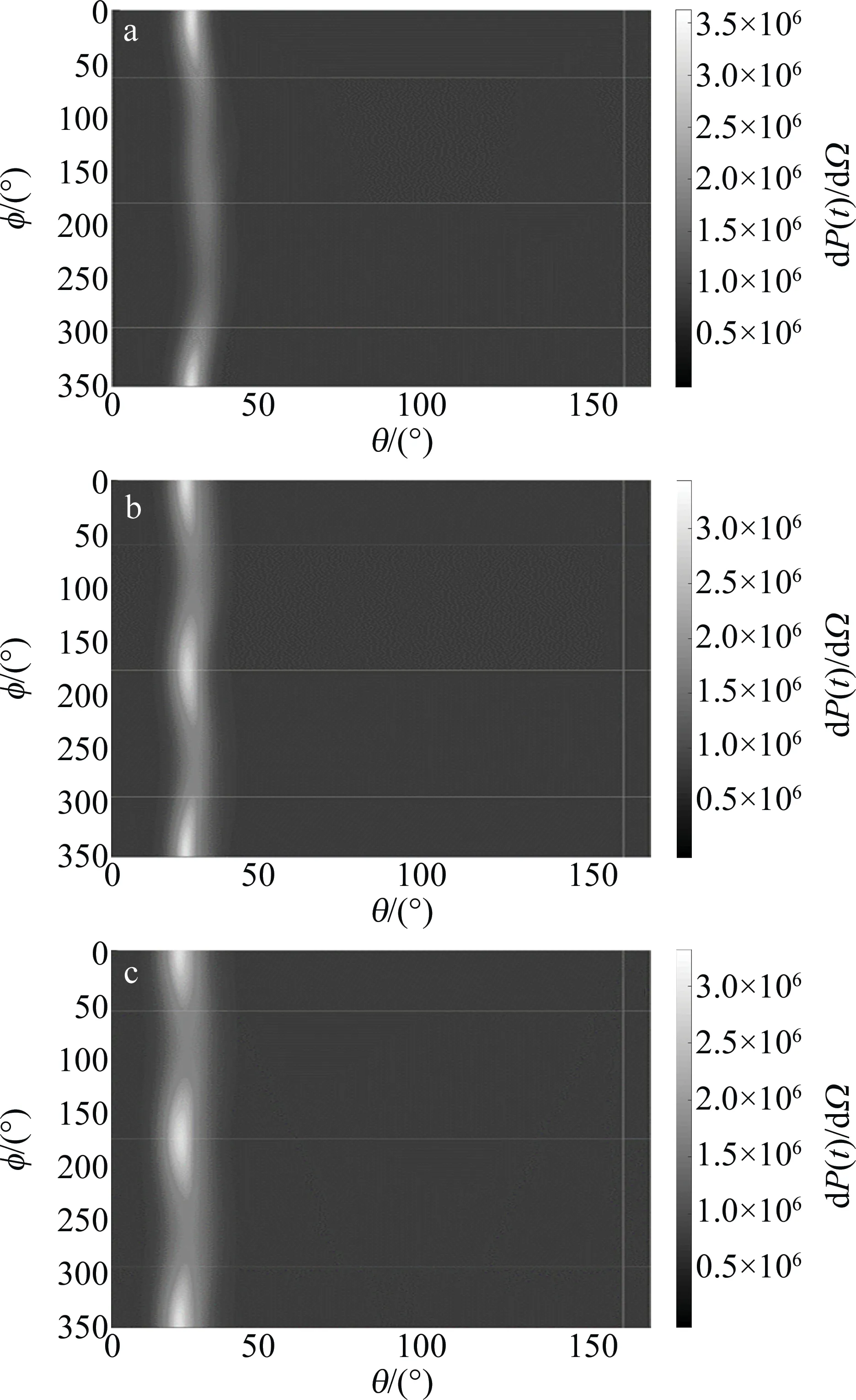
Fig.3 Influence of elliptical laser on the power of electron Thomson scattering under different pulse width

为探究激光脉宽对电子辐射功率最大值的影响，在L∈[0,10λ0]以0.1λ0为间隔取100组激光脉宽值。分别计算出其对应的电子辐射功率最大值，并绘制出电子辐射功率最大值随着激光脉宽的变化曲线,如图4所示。其中横坐标为激光脉宽，而纵坐标为在规定的激光脉宽下所对应的电子辐射功率角分布的峰值，其它入射激光参数同图3。电子的辐射功率峰值随着激光脉宽的的增大而减小，且减小的速度不断减缓。脉宽为10λ0时的峰值功率仅为脉宽为0.1λ0时的1%。这是由于电子的运动轨迹是螺旋线，当激光脉宽较小时，高能电子从激光脉冲中提取的纵向有质动力较小，因而电子的运动范围受到限制，辐射范围相对集中，辐射功率峰值较大。随着激光脉宽的增大，由于电子从激光脉冲中吸收了更多的有质动力，高能电子从聚焦方向被向前推进的运动范围扩大，导致辐射分散，辐射功率峰值较小。

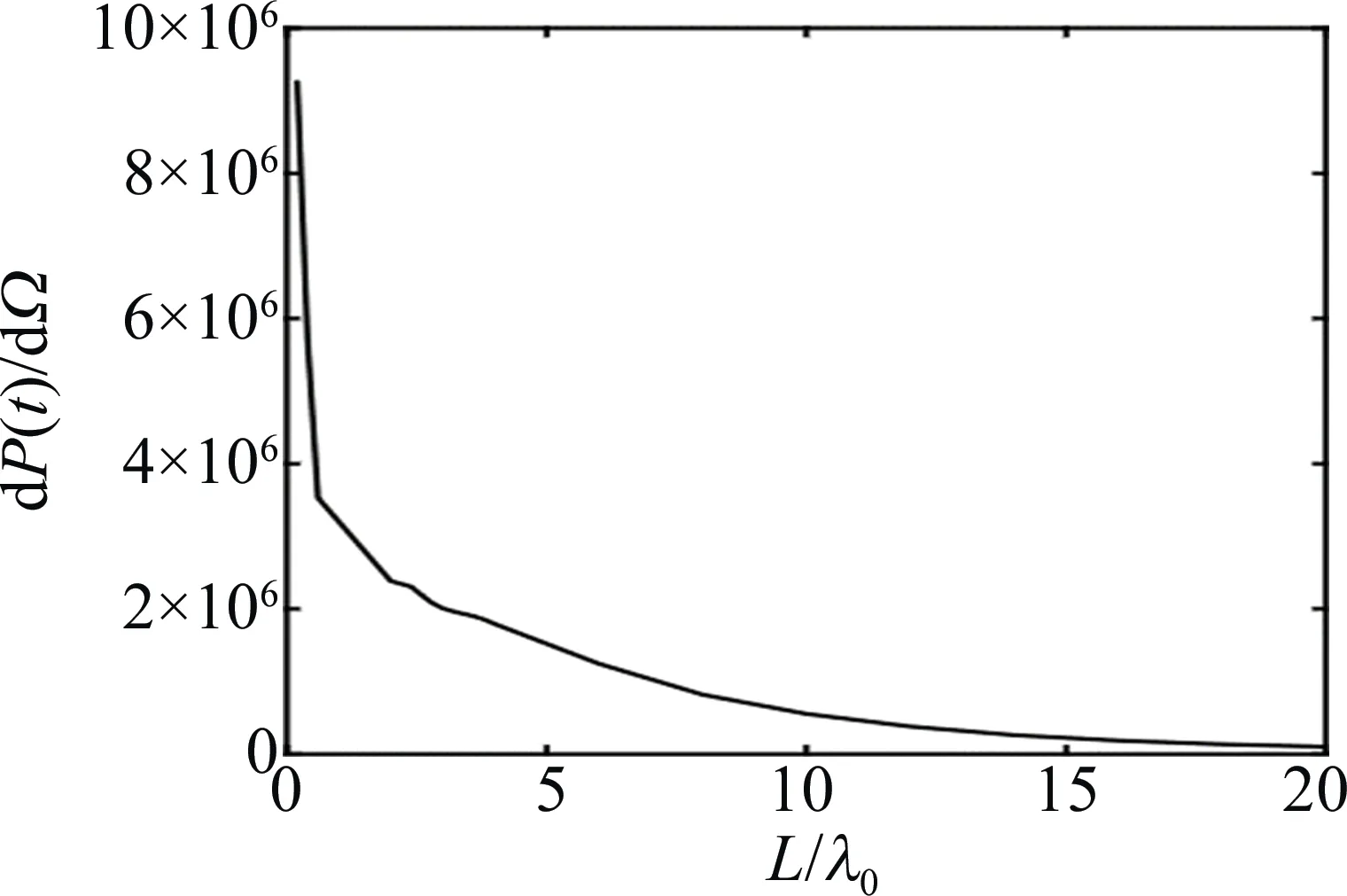
Fig.4 Influence of laser pulse width on the peak power of electron radiation

综上所述,随着入射激光的脉宽增大，电子的辐射功率峰值呈现下降趋势，且当激光脉宽较小时，其值的变化对于电子辐射功率峰值的影响较大，而在激光脉宽较大时，激光脉宽的变化对电子辐射功率峰值的影响较小。

为进一步分析激光脉宽对电子辐射功率峰值点特性的影响，分别做出了不同脉宽下电子辐射功率峰值点的时间谱和频谱图。

图5和图6中激光偏振参量、入射激光强度、束腰半径、相对论因子等参数同图2，τ0为一个激光周期,分别选取辐射功率峰值处的方位角φ0为6°，358°，358.5°，179°,θ0为26.25°，25.25°，23.25°，22.5°作出时间谱和频谱图。

Fig.5 Time spectrum of electron radiation power peak at different laser pulse width

随着激光的脉宽的增大，辐射峰达到峰值所需要的时间也相应变长(见图5a～图5d)，这是由于激光脉宽会影响到每个光周期中的电磁场强度，进而延后了电子的加速到峰值的时间。激光脉宽越宽，电子辐射功率的峰值越小，谐波次数越高(见图5a～图5d)。电子辐射脉冲最高峰的持续时间随着激光脉宽的增大而增大，产生的辐射脉冲具有单峰的特点(见图5e～图5h)。

在有限的脉冲持续时间内，电子运动被调制，单个谐波的集合转化为一个连续的频谱，其中大量的最大值和最小值相对于原始谐波发生偏移如图6a～图6d所示。光谱能量密度的包络也发生变化：光谱分布的宽度减小，而谱函数的峰值变小。但电磁辐射的角分布在定性上保持不变。同时激光脉宽的增大对于电子频谱函数的截止频率有显著的影响，随着激光脉宽的增大，电子频谱的截止频率不断减小，即高频分量减少，同时谐波次数增加。

Fig.6 Spectrum of electron radiation power peak at different laser pulse width

3 结 论

基于汤姆逊散射及电磁辐射理论，采用激光与单电子作用模型，从数值上模拟了不同脉宽的激光脉冲撞击产生的电磁辐射的能量峰值特性。以MATLAB为工具，采用控制变量法，对不同激光脉宽下电子辐射功率及时间函数、频谱分布进行了数值模拟，详细研究了椭圆偏振高斯激光脉冲激光脉宽与电子的辐射分布峰值功率的关系。研究结果表明，当紧聚焦激光脉冲遇到静止单电子，激光的有质动力推动电子向前运动，同时电子沿运动切线方向发出辐射；散射辐射在散射方向的中心呈尖锥状积累;随着激光脉宽的增加，辐射功率数值分布逐渐呈现出双峰形;激光脉冲宽度越宽，电子的辐射功率峰值呈现下降趋势，且当激光脉宽较小时，其值的变化对于电子辐射功率峰值的影响较大，而在激光脉宽较大时，激光脉宽的变化对电子辐射功率峰值的影响较小；辐射功率达到峰值所需实现越长，最高峰的持续时间越长，频谱函数的截止频率越低，高频分量变少，谐波次数增加。

所得结果对汤姆逊散射的辐射能量峰值的研究在中国环流器二号A装置(HL-2A)、激光空气等离子体状态诊断等方面都具有重要潜在应用[23]。