基于LLE激光双电弧复合焊接过程稳定性研究

王 耀，张洁琦，顾小燕

(1.山西机电职业技术学院 材料工程系，长治 046000; 2.九江职业技术学院 机械工程学院，九江 332100; 3.江苏科技大学 材料科学与工程学院，镇江 212003)

引 言

在焊接过程中，焊接电信号是最重要的参数，其中包含了大量能反映焊接电弧行为和熔滴过渡的信息。基于电参数的焊接过程监控和评价是保证焊缝质量提高生产效率的重要手段[1]。

非线性时间序列处理方法是一种用于量化混沌程度的重要手段，它被广泛地应用在生物医学、非线性电子学和机械工程领域，以及应用在一些焊接制造监控和评价中。LUO等人计算分析了点焊过程中的电极位移信号的混沌特征[2]。CAO等人描述了短路过渡CO2气体保护焊的稳定性[3-4],定量计算了方波交流埋弧焊不同参数下电流的最大李雅普诺夫指数(the largest Lyapunov exponent，LLE)[5]。实践证明，混沌现象不仅存在焊接过程中，而且混沌程度与焊接过程中的稳定性有关。焊接电信号的LLE可以作为焊接稳定性的指标。

激光-熔化极气体保护(gas metal arc,GMA)复合焊接是在激光-电弧复合焊接的基础上发展起来的一种新型高效焊接方法[6-8]，是将3个热源紧密接触，产生1个单一的高强度能量源[6-9]。与激光-电弧复合焊相比，激光-双GMA复合焊具有熔敷量大、间隙桥接能力强、熔深深等优点。激光-电弧复合焊轴对称且无方向性，所以不存在由于焊接方向引起的焊接质量问题[10-11]。此外，与激光-电弧复合焊相比，在激光-双GMA复合焊接中增加了一道电弧，降低了激光功率，节约了生产成本[12-13]。激光-双GMA复合焊是一个相对比较复杂的系统，但它是一种很有前景的焊接方法。由于能量、力和场的相互作用，激光-双GMA复合焊接是一个复杂的物理和化学冶金过程，有许多随机和不确定的影响因素。由于其高度非线性特征和参数间的相互耦合，很难建立反映其变化规律的质量评价数学模型[14-15]。

本文作者计算了不同焊丝间距下焊接电流信号的LLE，结合对电信号、电弧形态和熔滴过渡的观察，探讨了焊丝间距对激光双弧复合焊接稳定性的影响。

1 理论和算法

计算Lyapunov指数方法有多种，例如Wolf、Jocobian、C-C法等。相较其它方法，C-C法是一种高精度、计算量小的计算方式。本文作者采用C-C法来分析激光-双电弧复合焊接过程中电流信号的Lyapunov指数[16-17]。

C-C法的相关函数可以同时估算最优延迟时间τd和延迟时窗τw。嵌入维数m可通过公式τw=(m-1)τ获得。延迟时间τ和嵌入维数m是相空间重构过程的两个非常重要的参数，直接关系到相空间重构的质量。这里采用一种基于关联积分的统计量来描述非线性时间序列的相关性:

(1)

S(m,N,r,t)=C(m,N,r,t)-Cm(1,N,r,t)

(2)

式中，C(m,N,r,t)为关联积分;S(m,N,r,t)为统计量,由于S(m,N,r,t)的公式中含有两个关联积分函数，因此称为C-C法;r为搜索半径，σ/2≤r≤2σ(σ是时间序列的标准差);t表示时间序列;N为时间序列的数据编码;M=N-(m-1)τ是m维空间里的嵌入点数目;dij表示上确界范数。

为了研究非线性相关，计算t个不相交的时序。当N→∞时，对固定的m和t和所有的r，如果数据独立同分布，则S(m,r,t)=0，然而实际数据有限且存在序列相关，因此一般S(m,r,t)≠0。S(m,r,t)的局部最优时间不是零交叉就是关于r变化最小的时间。选择r的几个代表值，ΔS(m,t)则度量了关于r的变化。

取m=2,3,4,5,N=5000，代表值rk=kσ/2,k=1,2,3,4。

S(t)的平均值为:

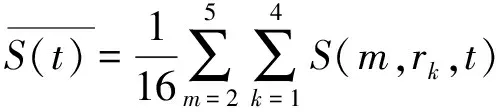
(3)

S(t)的变化量ΔS(t)的平均值为：

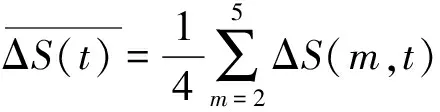
(4)

S(t)的估计值为:

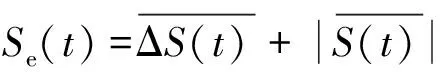
(5)

设t≤200，取下述统计量最小值，作为延迟时间窗τw的最优值。在重构拓扑空间时，可以从观测到的时间序列中通过基准轨迹来确定LLE，它可以度量附近轨迹偏离率。

对于拓扑空间里的每个点,计算出该点在j个离散时间后的距离dj(i)为:

dj(i)=dj(0)exp[λmax(Δt)]

(6)

式中,Δt为时间序列变化量;用最小二乘法作回归线，该线斜率即为LLE,定义为λmax。对于已知j，两边取对数后得到距离平均值为y(i)：

(7)

式中，q是所有非零dj(i)的数目。

本文作者利用MATLAB软件建立数学模型，对电信号数据进行处理，从而得到λmax。

2 实 验

激光双脉冲电弧复合焊接实验系统， 它包括一台交流焊机(Lincon INVERTEC V350-PRO)、两个自耗电极、两个送丝装置、一台最大输出功率2kW的Nd∶YAG激光器(JK2003SM)。波长为1064nm的激光束，由焦距300mm的透镜聚焦到工件表面大约0.8mm处。激光点位于两焊丝尖端连接线的中点。焊枪和工件夹角为60°。母材采用尺寸为310mm×150mm×12mm的Q235B低碳钢板，焊丝采用直径为1.2mm的H08Mn2SiA。干伸长度为15mm。保护气为氩气(质量分数为0.9999)，流量为20L/min。具体焊接参数见表1。

Table 1 welding process parameters

监控系统由电信号采集系统和高速摄影系统组成。电信号采集系统包含两个电流传感器和两个电压传感器，分别记录焊接过程的焊接电流和电弧电压。采用频率为10kHz的PCI-1742数据采集卡采集焊接电流，采集时间为8s。从采集库中随机抽取50000个数据点，定义LLE为λmax,计算λmax及其焊接系统中的标准偏差σ(λmax)。利用高速摄像机(CPL 250 K CMOS)垂直放置于焊接方向，采样频率为1000帧/s，对熔滴过渡和等离子体行为进行同步监测。

3 结果与讨论

3.1 焊丝间距对焊接过程稳定性的影响

首先，分析双电弧焊接中两个电弧之间的相互作用。电流沿同一方向流过焊丝,分别设两根电线中的电流为I1和I2，弧柱半径为r1和r2，D是焊丝间距，电流1至电弧2的电磁力为F1,2，电流2至电弧1的电磁力为F2,1，α,β是焊枪倾角,如图1所示。

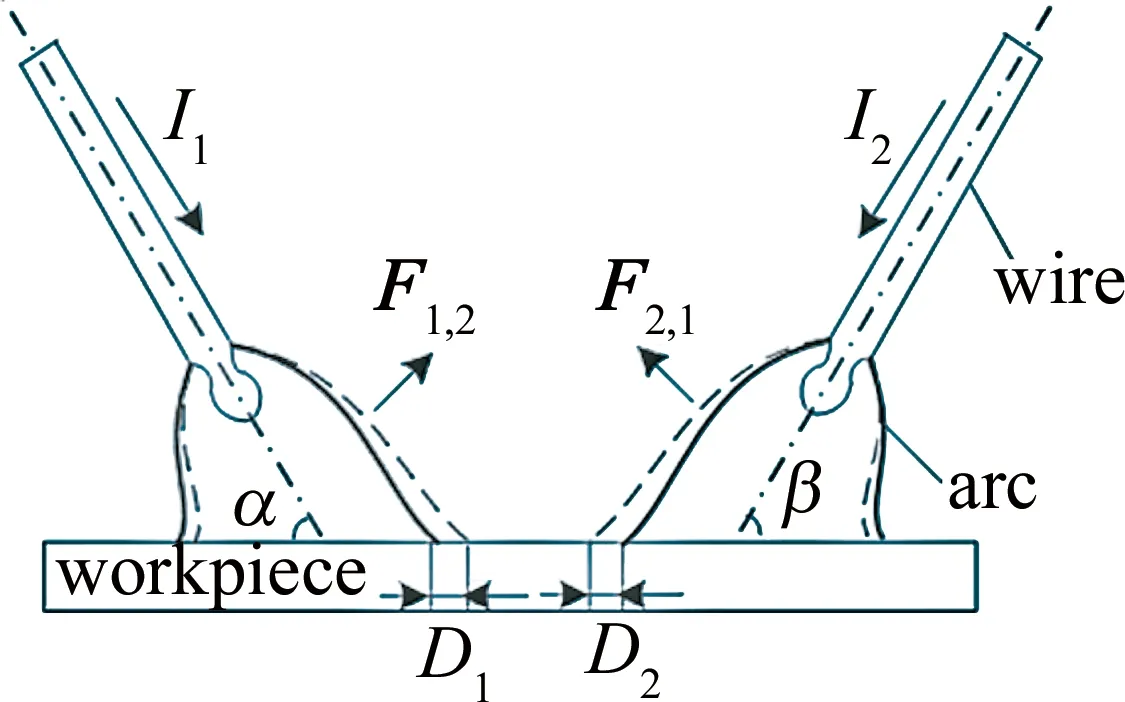
Fig.1 Electromagnetic force of laser double arc welding

根据电磁学理论，由两电弧产生的磁场可以表示为：

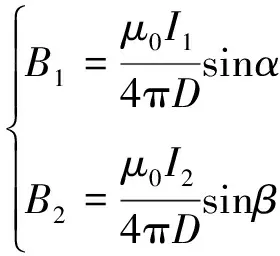
(8)

式中，μ0表示磁导率。两电弧间的作用力可推导如下：

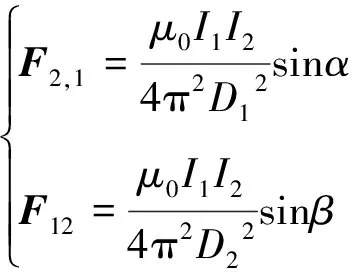
(9)

由此可以看出，电弧之间的吸引力取决于两个电弧的电流方向和焊丝间距。 此外，吸引力与焊枪的角度也有关系。 由于电磁场作用，两电弧弧偏离了焊丝，假设两焊枪的角度相同，电弧1的偏差是D1，弧长是L1，电弧2的偏差是D2，弧长为L2，偏差可以表示为：

(10)

可以推断，偏差由焊接电流、电弧长度(与电弧电压有关)和焊丝间距决定。 电流越小，弧长越长，偏差越大，说明电弧的刚度越弱[18-19]。因此，在双弧焊接过程中，电弧的偏差会导致断弧、熔滴过渡不均匀，难以实现稳定的焊接过程。

在YAG激光+双电弧复合焊接的情况下，当辐照度达到105W/cm2，在激光冲击工件表面的位置，工件材料发生明显汽化，从而形成小孔。原子、电子和离子等大量粒子从“小孔”喷发出来。由于金属原子比保护气体电离电势低得多，当金属原子在电弧热的作用下快速电离时，等离子体的有效电离电位降低，形成了一个导电通道。电弧沿着电阻最小的路径，在通道中稳定燃烧，电弧根固定在“小孔”中，称为“钉扎效应”[20-22]。在此次研究中，激光功率为1.5kW，焦点直径为0.8mm；辐射密度为2.3×105W/cm2。 因此，在一定的工艺条件下，由于激光对电弧的导向和稳定作用，实现了稳定的焊接工艺。

在YAG激光+双电弧复合焊接过程中，激光和电弧间的相互作用分析如下。激光束中的电子不定向运动，很难产生电流。因此，激光束产生的电场可以忽略不计。电弧不受激光束的影响。

假设电弧1对激光离子体的电磁力是F1，p，电弧2对激光等离子体的电磁力F2,p，如图2所示。

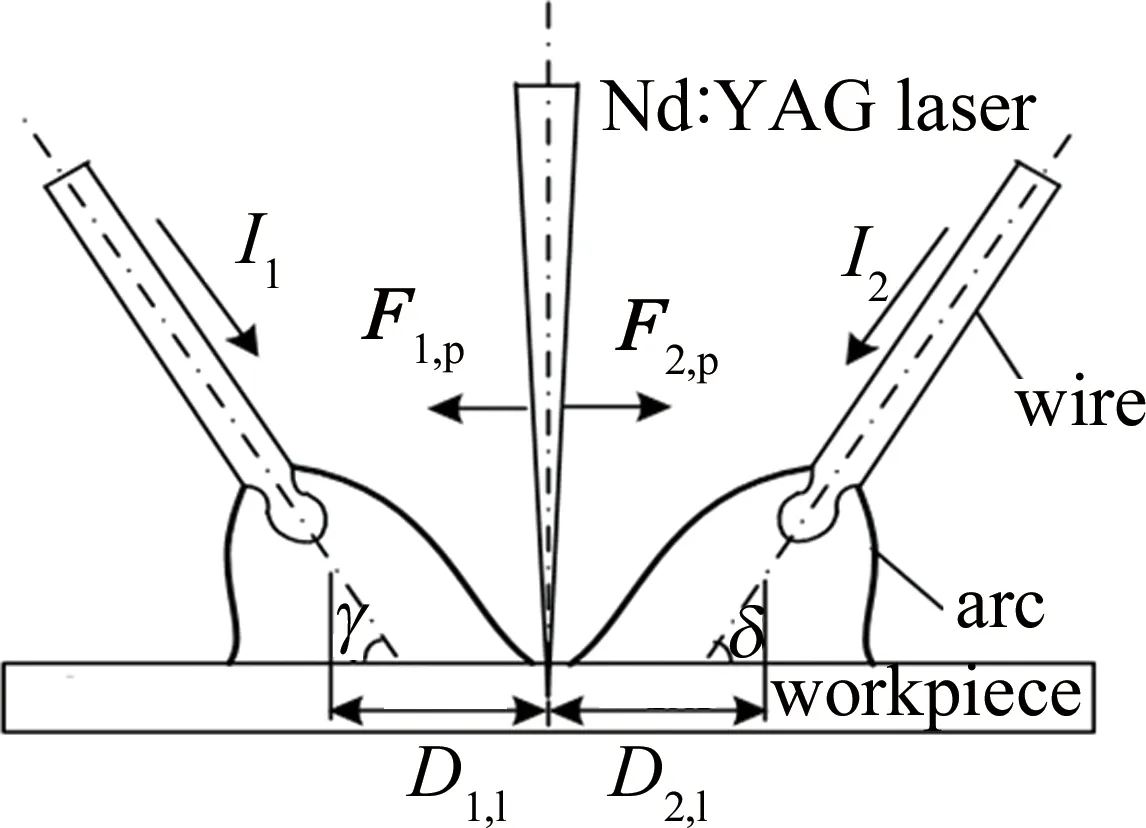
Fig.2 Force diagram of laser induced plasma in laser+double arc hybrid welding

(11)

式中,Ip是激光等离子体中的电流，rp是等离子体半径，D1,l是电弧1与激光束之间的距离，D2,l是电弧2与激光束之间的距离,γ和δ是焊枪倾角。

在单电源模式下YAG激光+双电弧复合焊接过程中，两个电弧的电压大致相等，两电弧产生的磁场大致相同，等离子体的力主要取决于电磁力。激光等离子体将会偏离较大电磁力的电弧，同时受激光点的约束，等离子体的位置和形状在宏观上会发生变化，在微观方面，等离子体中的带电粒子在电场力和洛伦兹力作用下运动，等离子体内电子的分布也会发生变化，打破了原来的平衡状态。这样一来，激光等离子体的性质就会发生变化，对电弧的稳定作用将减弱。

3.2 YAG激光+双弧焊接过程的稳定性

在两个电弧电压相等的前提下，分析YAG激光+双弧焊接过程的稳定性，可分为4种情况。

(1)当两电弧间间距Da,a非常小(例如0mm～3mm)时，两弧在电磁力的作用下都会产生较大的偏差。当激光束以高密度穿过电弧区时，根据逆轫致辐射机制，激光能量被电弧等离子体吸收。在这种情况下，激光能量到达工件表面的能量很小，存在“钉扎效应”，两弧之间的引力增强了干涉效应。由于两弧之间的电磁力很强，电弧阴极斑点的漂移不可避免。 如图3所示,当Da,a=0mm时，两电弧在激光等离子体上方剧烈弯曲燃烧，电弧在脉冲电流的作用下容易与激光等离子体分离，导致断弧，焊接过程不稳定。

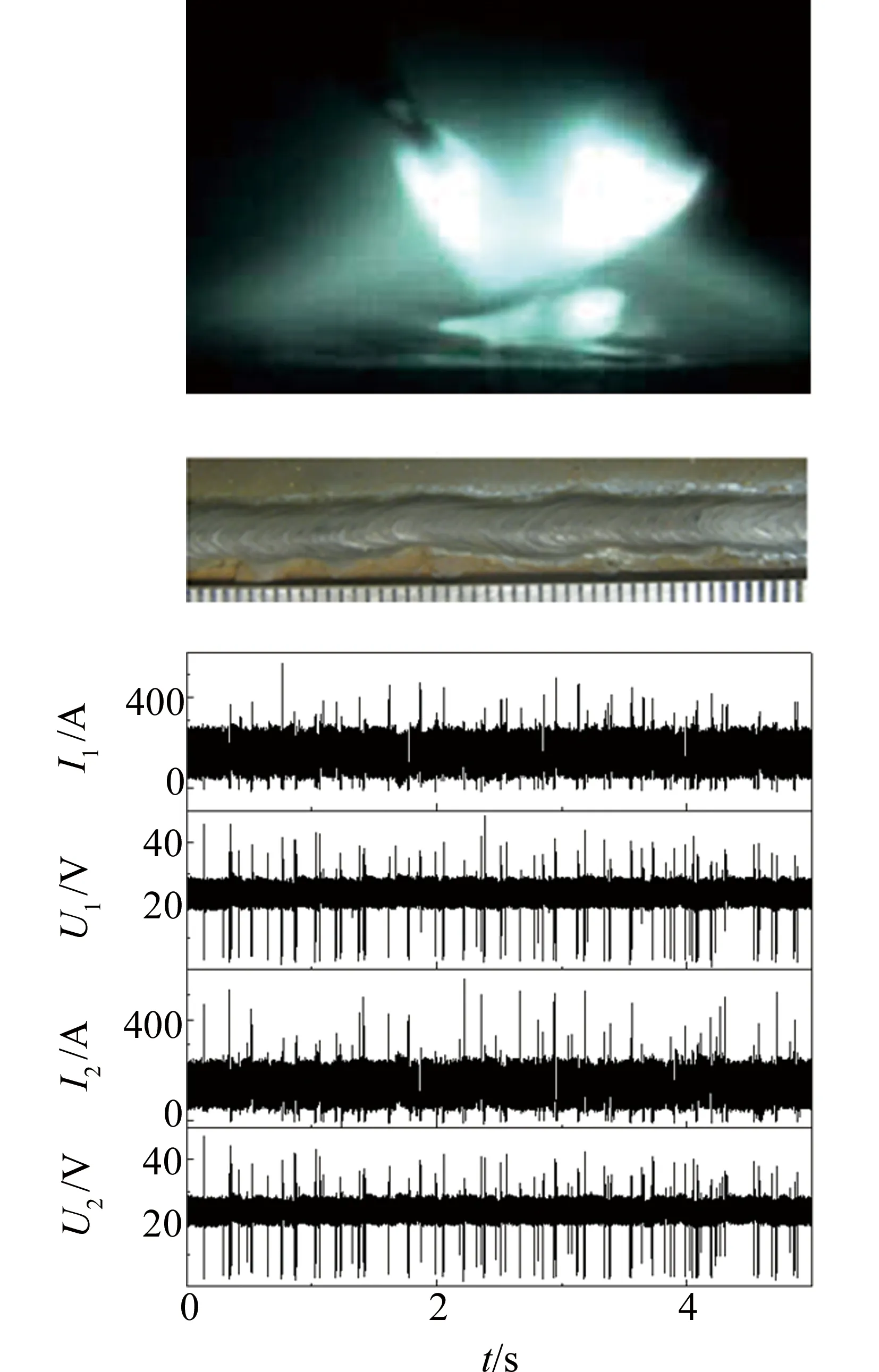
Fig.3 Arcs shap, weld bead and electrical signal when Da,a=0mm

当Da,a=0mm时，焊丝末端熔化形成熔滴。两个焊丝末端的熔滴在电磁力的作用下偏离了各自的轴线，并逐渐合并成一个更大的熔滴。在重力和等离子体射流力的共同作用下，合并的熔滴增大并过渡到熔池中。完成一个过渡周期需要12个脉冲。 此外，在该过程中，熔滴形成过多，与熔池接触频繁，故发生短路过渡。电弧由于两弧之间的强烈干扰而不稳定，且熔滴过渡为大颗粒过渡，导致焊接飞溅过大。图3中,Da,a=0mm时5s内的电信号表明，焊接过程中焊接电压和电流波动较大，熔滴过渡主要为短路过渡。

(2)当Da,a为中间值、激光束偏离其中一个电弧时，离激光束最近的电弧产生的电磁力比远离激光束的电弧产生的电磁力强。在不平衡力作用下，激光诱导等离子体在不平衡力的作用下向较大电磁力电弧弯曲，从而远离另一个电弧。

当激光等离子体与近端电弧等离子体耦合时，在洛伦兹力和电场力的作用下，激光等离子体中的自由电子向电弧等离子体移动，从而导致激光等离子体另一端的电子数量减少。 电子数量的急剧减少，不再需要为电弧燃烧提供足够的电子。根据电弧倾向于电子密度集中区，远离激光点的弧根会向激光等离子体的上部偏移，并引起较大弯曲。焊丝轴线上电磁力和离子流的减小，使得熔滴过渡困难。随着焊丝的熔化，熔滴逐渐长大，重力逐渐增大。 最后，当重力增加到足以克服过渡阻力时，熔滴转移到熔池，这是一种不稳定的球状排斥过渡。在这种情况下，远离激光束的电弧激光稳定性较小，在熔滴落入熔池时，电弧的阴极斑点很容易从激光等离子体的顶部移动到工件的表面，从而导致电弧和激光束的分离。在这种情况下，电弧和熔滴过渡都不稳定，无法实现稳定的焊接过程。

Fig.4 Arcs shap, weld bead and electrical signal when D1,l=2mm，D2,l=5mm

图4为D1,l=2mm和D2,l=5mm时电弧形态、焊道和电信号。靠近激光束的弧根被约束在“小孔”附近，呈现出复合电弧的特征。 熔滴过渡是稳定的一滴一脉冲，远离激光束的弧根向上弯曲，熔滴严重偏离焊丝轴向，甚至冲出了熔池，飞溅较大。

D1,l=2mm和D2,l=5mm时5s内的电信号表明，由于激光束的稳定性，靠近激光束电弧的电压和电流波形没有存在异常波动。 然而，由于阴极斑点的漂移，远离激光的电弧的电流和电压信号波动明显。

(3)当Da,a为中间值、两弧之间的距离适当、且激光束位于两弧的中心时，两弧对激光束的反电磁力相等。激光等离子体的电子在两弧产生的洛伦兹力和电场力的作用下大致平衡，电子均匀分布在等离子体两侧。激光等离子体为两弧提供自由电子，电弧稳定。

图5所示为Da,a=7mm时的电弧形态、焊道和电信号。可以看出,在两电弧电磁力作用下，激光等离子基本处于平衡状态。激光等离子体和两弧相互耦合良好，激光等离子体为两弧提供稳定的电离通道，防止弧根的漂移。从Da,a=7mm时5s内的电流信号可以看出，在整个焊接过程中无异常波动，焊接过程稳定。

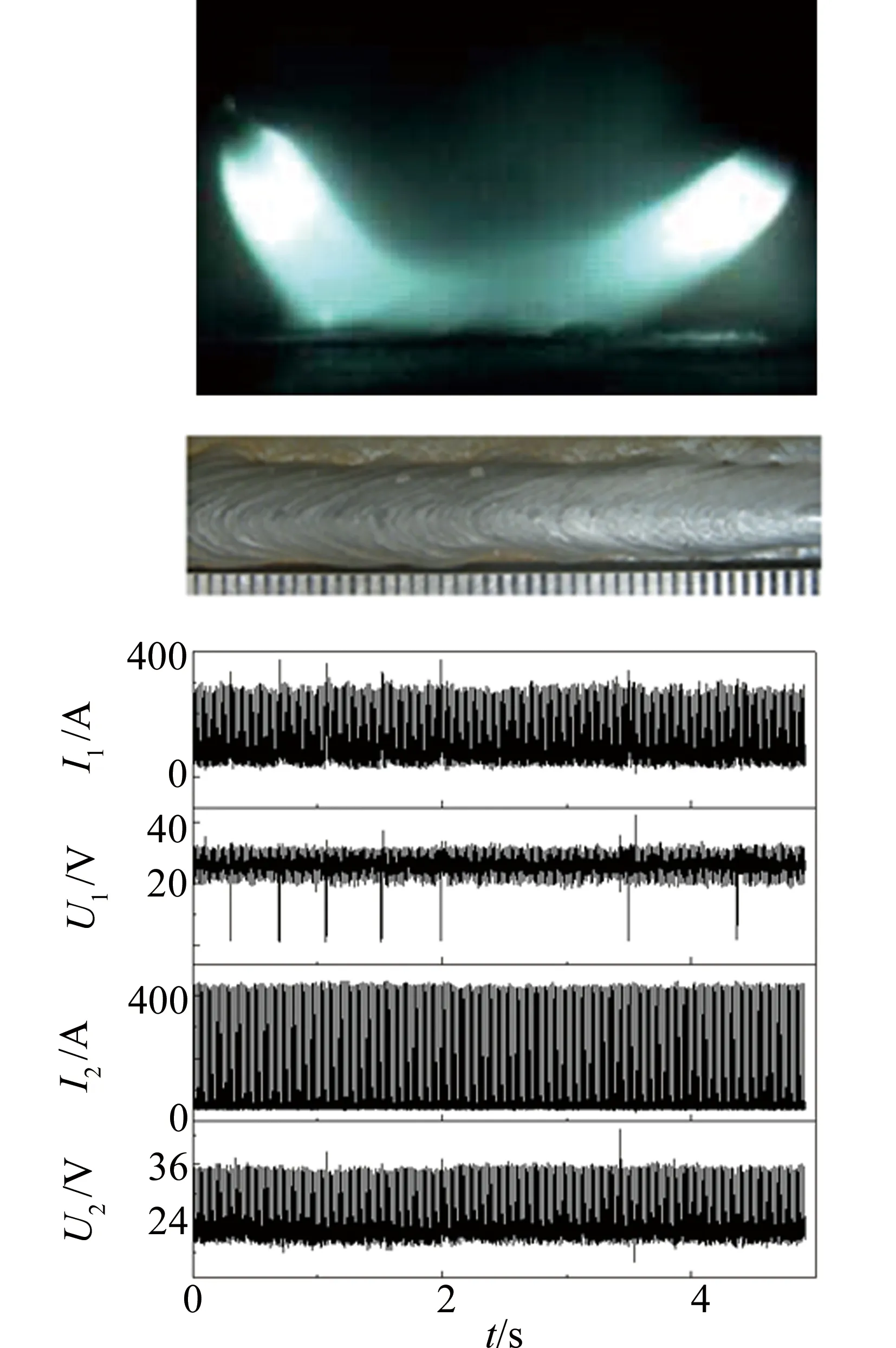
Fig.5 Arcs shap, weld bead and electrical signal when Da,a=7mm

(4)当Da,a足够大时(通常超过9mm)，激光束与电弧之间的电磁力显著降低。图6为Da,a=12mm时的电弧形态、焊道和电信号。激光等离子体与电弧之间不存在耦合效应。在高速焊接条件下，焊接速度超过了电弧移动速度，导致电弧漂移，激光束不稳定。在单电源模式，两电弧交替燃烧。

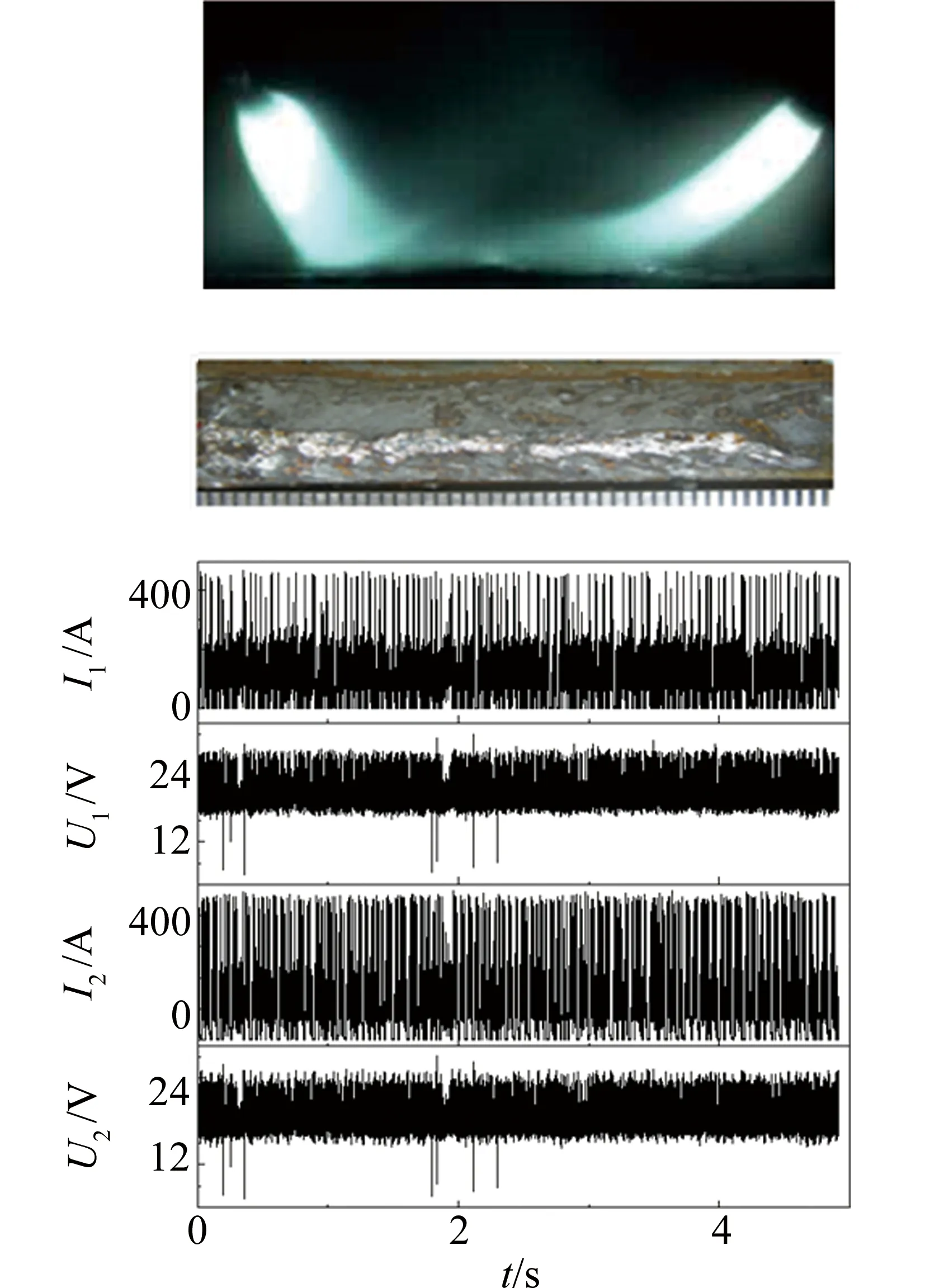
Fig.6 Arcs shap, weld bead and electrical signal when Da,a=12mm

Da,a=12mm时，单电源模式下两电弧与激光束分离，周期性地交替燃烧。熔滴过渡周期为0.018s，熔滴过渡为稳定的一脉冲一滴。然而这种情况下，没有激光和电弧的耦合效应，复合焊接是毫无意义的。

3.3 基于LLE的焊接过程稳定性评价

以上基于观察法的研究和分析只能定性地分析激光双弧复合焊接过程中不同弧间距焊接稳定性，有必要采用定量分析和定性分析相结合的方法，来全面研究焊丝间距对焊接过程稳定性的影响。图7中给出了不同焊丝间距焊接电流的λmax及其标准偏差σ(λmax)的计算结果。

焊接电流的λmax的计算结果为正，表明激光+双电弧复合焊接过程处于混沌状态。 因此，λmax可以反映过程中的混沌程度。λmax越小，焊接过程的混沌程度越小，相应地，焊接过程越稳定。

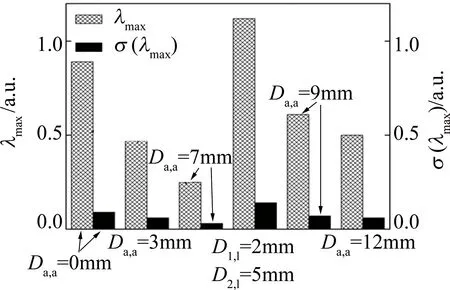
Fig.7 Welding current λmax and standard deviation of different wire spacing σ(λmax)

当激光束偏离至其中一个弧时(D1,l=2mm，D2,l=5mm)，激光等离子体中电子分布不均匀，导致两个电弧受力不平衡，导致焊接过程中严重不稳定，λmax达到最大值1.12。

当激光束位于两弧中心时，焊丝距离分别是0mm,3mm和7mm，λmax分别是0.89,0.47和0.25。结果表明，随着焊丝间距从0mm增加到7mm，激光对电弧的稳定性增强，因此焊接过程的稳定性提高。当距离持续增加到9mm，甚至是12mm时，λmax值减少到0.61和0.56。虽然焊接过程再次呈现稳定的趋势，但激光等离子体和两个电弧不再相互耦合，激光焊接和电弧焊接分别表现出各自的特性。 焊接过程中能够满足激光与电弧良好耦合、焊接过程稳定的最佳焊丝间距约为7mm(激光位于两弧中心)，计算结果与观测结果吻合。同样也可以通过焊接成形来验证。

结果表明，当间距为7mm时(激光位于两弧中心)，焊缝表面平整光滑，且熔深最大。 激光偏离到其中一个弧会引起大量的飞溅，导致焊接过程不稳定。焊丝间距过大或过小都会导致焊缝熔深减少。 因此，在这种焊接条件下，焊接过程稳定得到的λmax<0.61。 既能满足热源的良好耦合，又能满足焊接过程稳定的最佳焊丝间距为3mm～9mm，激光束位于两条弧的中间的最佳焊丝间距为7mm。

4 结 论

LLE反映了焊接系统的混沌程度，为焊接稳定性提供了判据。不同焊丝间距下焊接稳定性的计算结果与电信号、电弧形状和熔滴过渡的观察结果吻合较好，既能满足热源的良好耦合，又能满足焊接过程稳定的焊丝间距为3mm～9mm，激光束位于两条弧的中间时焊丝间距为7mm。

本文中以激光+双电弧焊接中的焊丝间距为例，探讨了Lyapunov指数评价焊接过程稳定性的可行性。 这项研究虽然可行，但还需继续深入。 下一步将结合焊接性能来获取λmax，电弧稳定则可以进一步优化焊接参数。本研究也可用于评价其它焊接过程的稳定性。