智能手机传感器技术在高中物理课堂教学中的应用——以探究向心加速度与角速度、转动半径之间的定量关系为例

闫彩霞

（山东省青岛第二中学物理学生发展研究室，山东 青岛 266061）

利用传感器进行实验与传统实验相比较更为快捷、准确，并且数据采集与记录的容量也大幅度增加.随着技术的发展，一些精巧的传感器开始被搭载在智能手机上，这些传感器包括加速度传感器、声传感器、光传感器、霍尔传感器（测量磁场强度）、陀螺仪传感器（测量角速度）等.同时随着人们生活水平的提高和通信行业的发展，智能手机已经在学生（中学生）群体中普及开来.这种高普及率为智能手机与物理教学的结合提供了良好的契机.近年来SPARKvue、Sensorkinetics、Physicstoolbox、Phyphox等各类传感器手机应用软件也相继开发出来.本文以SPARKvue、Sensorkinetics两款手机软件为例，自主搭建实验装置，探究匀速圆周运动过程中向心加速度、角速度和转动半径之间的定量关系.突破向心加速度表达式仅通过理论推导进行教学的局限，进一步在实验教学中切实促进学生核心素养能力的提升.

1 用智能手机研究的实验装置及原理

1.1 实验装置

实验仪器：可调节转速的电机1台，硬木板一块（长度约1.5 m、宽度约5 cm、厚度约2 cm），2部相同的智能手机（手机中分别安装有“SPARKvue”软件和“Sensor Kinetics”软件），胶枪一把，热熔胶和胶带若干.实验装置示意图如图1所示.

图1 实验装置示意图

1.2 实验方法

（1）探究向心加速度的大小与角速度大小之间的定量关系.

将两部手机在距转轴相同距离的地方（转轴两侧）用胶带固定在转杆上，确保在转动过程中两部手机的转动半径不变.一部手机打开SPARKvue软件，用以记录转动过程中的向心加速度的大小.另一部手机打开Sensorkinetics软件，用以记录转动过程中的角速度的大小.然后通过调节电机的转速，使得转杆能够以不同的且稳定的角速度转动.最后将两部手机记录的相对应的向心加速度的和角速度的数值导入Excel中进行数据处理与分析.

（2）探究向心加速度的大小与转动半径之间的定量关系.

将两部手机在距转轴相同距离的地方（在转轴的两侧）用胶带固定，在实验过程中将两部手机同步远离转轴，并将手机加速度传感器距转轴的距离纪录下来.一部手机打开SPARKvue软件，用以记录转动过程中的向心加速度大小.另一部手机作为配重.然后打开电机的开关，使得转杆能够以一个稳定的角速度转动.最后将手机记录的对应的向心加速度和转动半径的数值导入Excel中进行数据处理与分析.

1.3 手机传感器介绍

手机内部装有Acceleration sensor，其各轴方向如图2所示.当转杆做匀速圆周运动时，只有指向轴心的向心加速度.使得手机的home键对准轴心，即可通过记录y轴的加速度来测该位置的向心加速度大小.SPARKvue软件可用来记录并显示手机内部Acceleration sensor所测得的加速度的变化情况.

图2 手机3条坐标轴方向

手机内部还装有Gyroscope sensor，可以记录各轴角速度的变化情况，其各轴方向如图2.使得手机的home键对准轴心，即可通过记录y轴的角速度来测该位置的角速度大小.Sensorkinetics软件可用来记录并显示手机内部Gyroscope sensor所测得的角速度的变化情况.

2 实验数据与讨论

2.1 探究向心加速度大小与角速度大小之间的定量关系

（1）原始数据收集.

通过手机1采集到手机在转动过程中的角速度变化情况如图3所示.由图可知曲线的前段部分为启动阶段的角速度变化，后半部分为结束阶段的角速度变化，中部为匀速圆周运动部分的角速度变化情况.通过放大即可准确读出角速度的大小为15.7 rad/s，如图4所示.通过手机2可记录向心加速度的变化情况，如图5所示.曲线的前部和后部分别为启动和结束阶段，中部为匀速圆周运动过程中向心加速度的变化情况，可由图读出加速度大小为24.8 m/s2.相同半径下，不同转速下对应的加速度的大小与角速度大小同样用该方法得出，相关内容不再赘述.

图3 角速度变化曲线

图4 匀速圆周运动阶段角速度放大图

图5 向心加速度变化曲线

（2）数据处理.

通过改变12次转速，保持转动半径不变，可得到向心加速度的大小与角速度的大小对应关系，作出向心加速度大小随角速度大小变化的图像如图6所示.

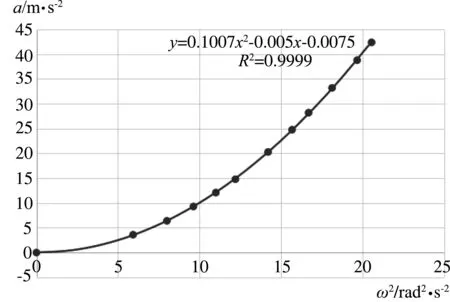
图6 向心加速度大小随角速度大小变化曲线

为进一步验证向心加速度大小是否与角速度大小的平方成正比，作出向心加速度大小与加速度大小的平方的对应关系如图7所示.

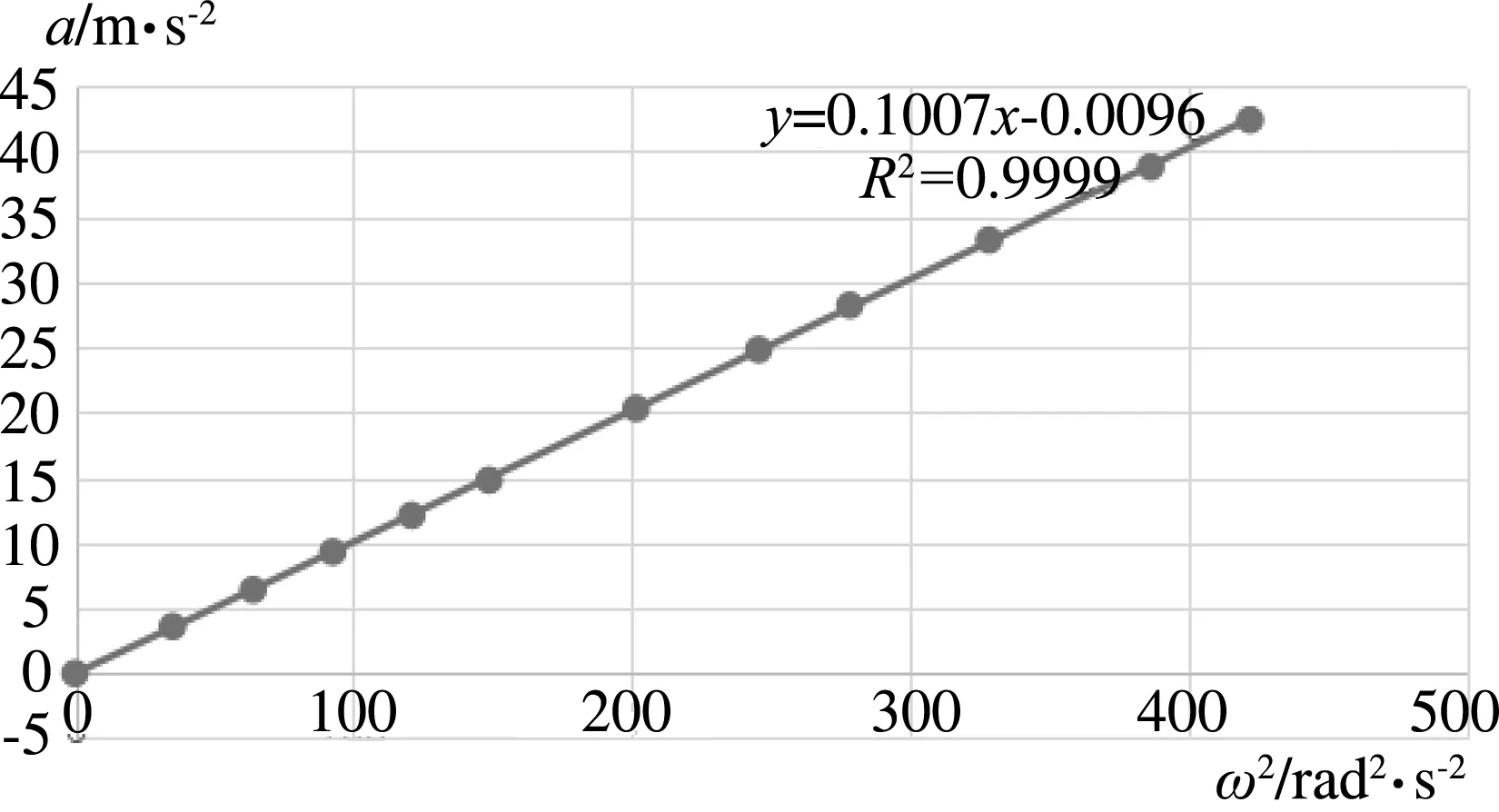
图7 向心加速度大小随角速度大小的平方变化曲线

综上可得，在误差允许范围内，转动半径一定时，加速度的大小与角速度大小的平方成正比.图像的斜率为0.1007与转动半径0.095 cm在误差允许范围内相等，即比例系数为转动半径的大小.

2.2 探究向心加速度的大小与转动半径之间的定量关系

（1）原始数据.

通过手机2的记录，可以得到在半径分别为0 cm、18 cm、20 cm、22 cm、24 cm、26 cm、28 cm 情况下的向心加速度的大小分别如图8-图13所示.

图8 18 cm半径向心加速度变化曲线

图9 20 cm半径向心加速度变化曲线

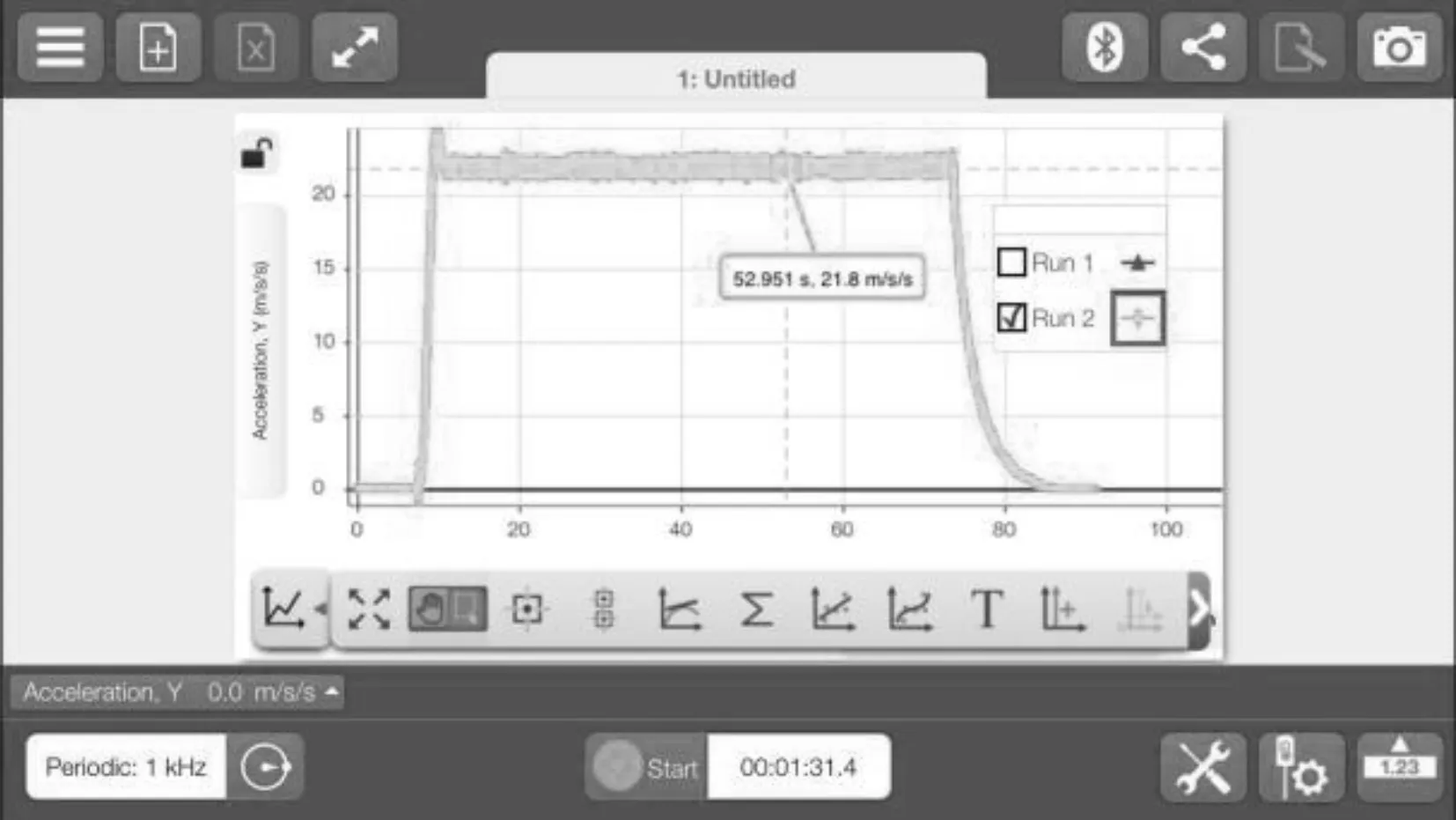
图10 22 cm半径向心加速度变化曲线

图11 24 cm半径向心加速度变化曲线

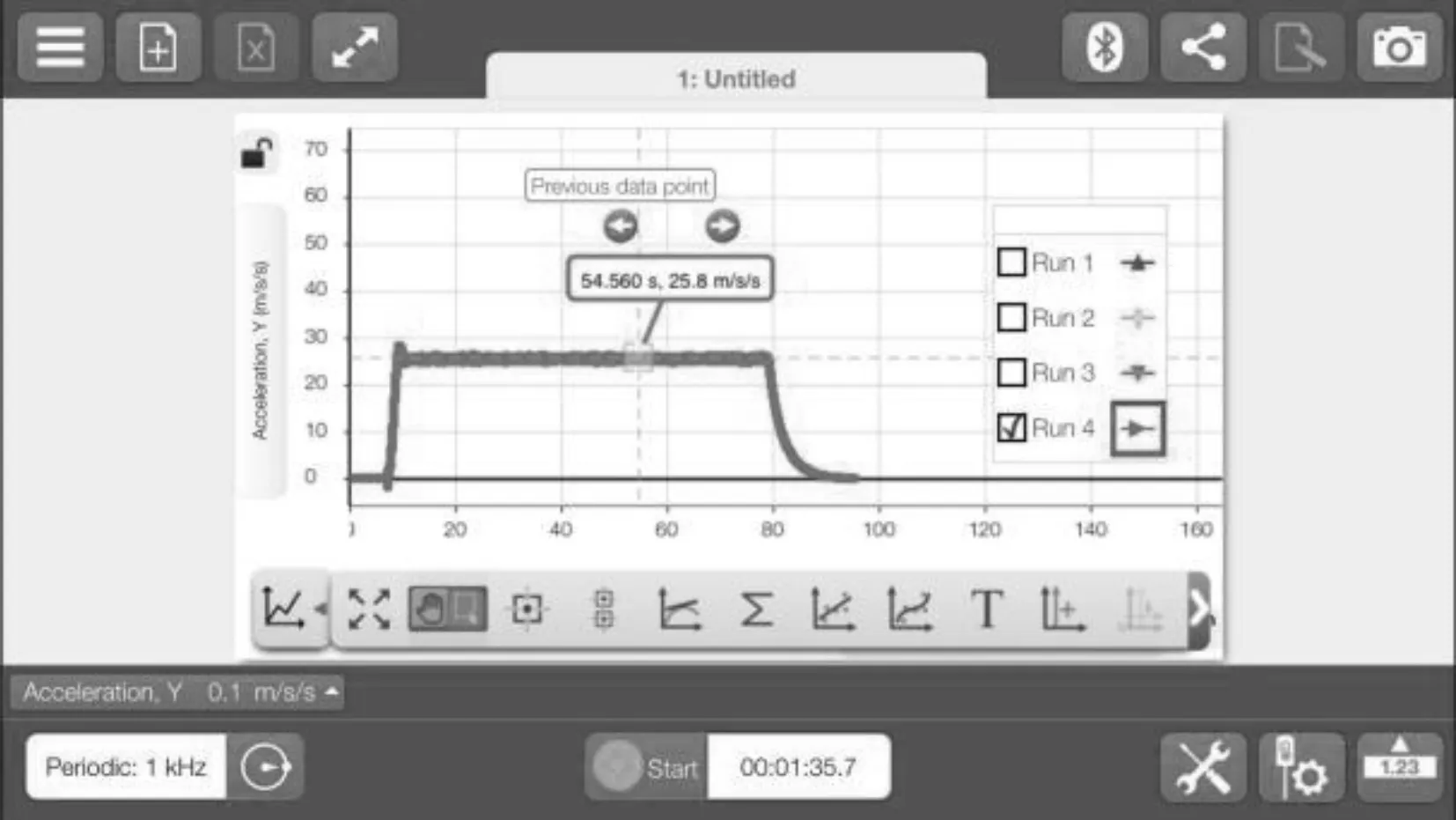
图12 26 cm半径向心加速度变化曲线

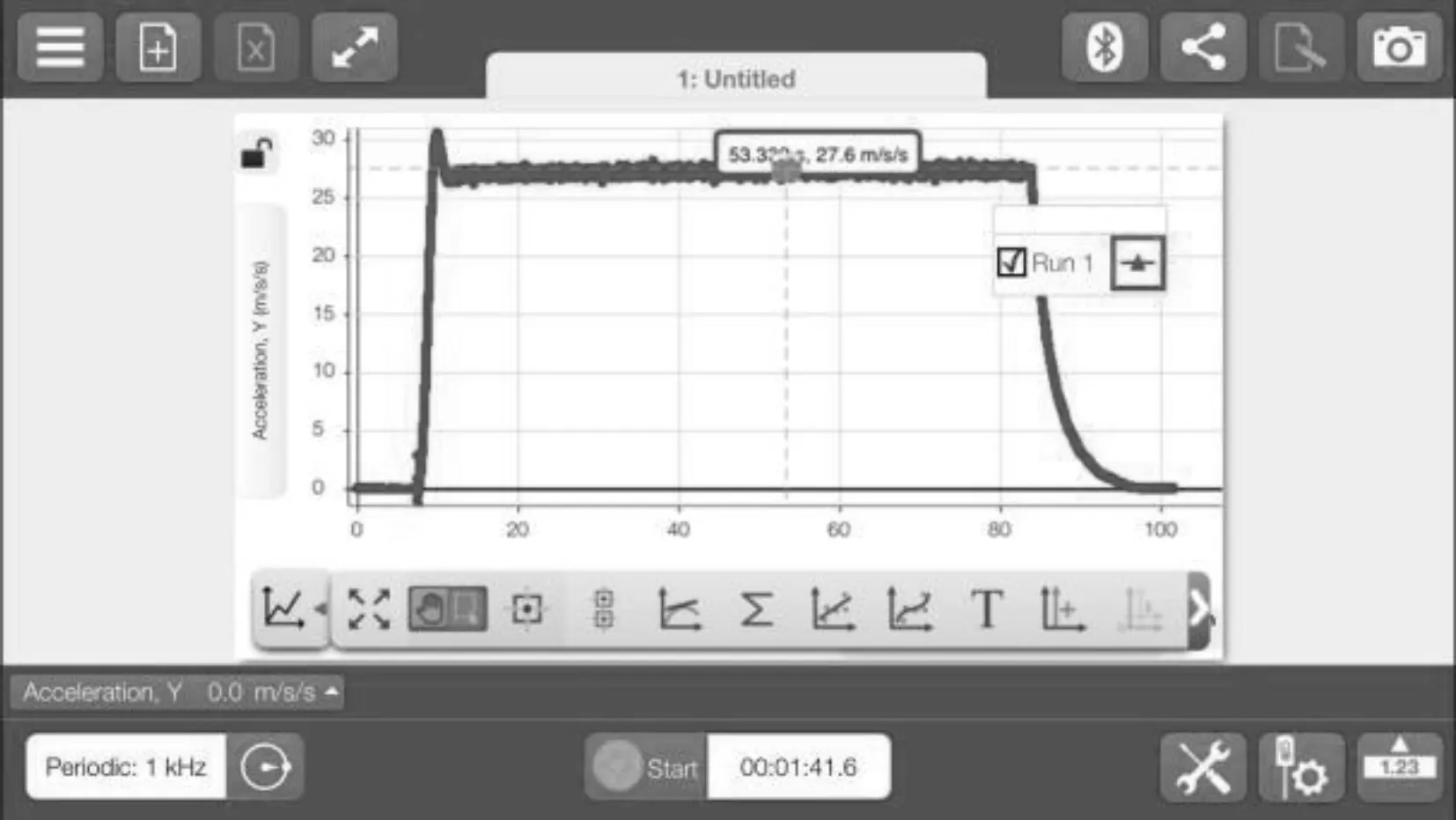
图13 28 cm半径向心加速度变化曲线

（2）数据处理.

根据记录的数据作出向心角速度的大小随转动半径的变化图像如图14所示.

图14 向心加速度随半径变化曲线

由上可得，在误差允许范围内，角速度一定时，向心加速度的大小与转动半径成正比.图像斜率为99.159，而角速度大小的平方的数值为98.75（加速度大小如图15所示），故比例系数为角速度大小的平方的数值.

图15 匀速圆周运动阶段角速度的变化曲线

综合以上探究可得向心加速度的表达式为a=ω2r.

3 误差分析

3.1 转动半径的确定

由于Acceleration sensor在手机位置中的确定存在一定的误差（对于iPhone6 Plus，经测定该传感器在距离手机下边缘约9.5 cm的地方），以及转轴并不是一个点而是直径约为1 cm的轴，使得转动半径的确定有一定的误差.也使得向心加速度的大小随转动半径变化的拟合直线有一个微小的截距.

3.2 数据采集的稳定性

由于一般电机很难提供绝对稳定的转速，所以在匀速圆周运动阶段两个传感器采集的数据都会有微小的浮动，使得最终数据出现一定的误差.

4 结语

该实验利用智能手机传感器探究出了向心加速度的大小与角速度大小的平方成正比，与半径成正比的实验结果，从而通过实验推导出了向心加速度的表达式.突破向心加速度表达式仅通过理论推导进行教学的局限，进一步在实验教学中切实促进学生核心素养能力的提升.同时传统的Dislab传感器实验也可以进行此实验的探究，但装置复杂且价格昂贵，不利于在中学教学中推广使用，特别对于比较偏远的地区.而该装置成本低、材料简单、实验现象明显，测量结果完全可以与之媲美，更有利于促进学生实验技能和创新能力的培养.

目前国内的选修课程、校本课程、研究性学习、课外实践等都为智能手机传感器实验探究应用提供了良好的环境，若能加以开发，不仅可以激发学生的学习兴趣，还能培养学生的综合素质.目前大部分的学校和学生并不配备传统的传感器设备，但几乎每个学生都有智能手机，而且两者的实验效果相差无几.所以智能手机传感器实验更有利于学生探索身边的世界，促进核心素养能力的发展.