有限简单连分数的逼近原理在Pell 方程上的应用
邓从政
(凯里学院,贵州凯里 556011)
0 引言
形如x2-dy2=±1 的不定方程即Pell 方程,当其参数d为开方开不尽的正整数时,用一般的初等方法难以求解,解析其解的构造更加困难.其解的形态与有限简单连分数貌似相距甚远,却有着紧密的联系.本文从有限简单连分数的性质及其与有理分数的关系出发,巧用有限简单连分数的独特性质,用逼近原理来探讨两类Pell方程的解法及其解的关系,从理论上阐述用逼近原理解Pell方程的有效性,并为研究这类不定方程解的构造提供一个简洁而实用的方法.
1 关于有限简单连分数的几个定理
定义设a0,a1,a2,⋅⋅⋅是一个无限整数列,aj≥1,j≥1.记有限简单连分数
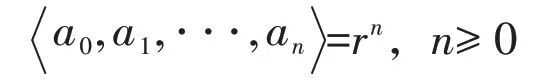
定义整数列{hn}与{kn}:
则,h0=a0,h1=a1a0+1,1=k0≤a1=k1<k2<⋅⋅⋅<kn<⋅⋅⋅,kn→+∞.
这里的{aj},{hn},{kn}就相当于有限简单连分数定义中取整数的特殊情形[1].
定理1有限简单连分数,n≥0的值是有理分数,
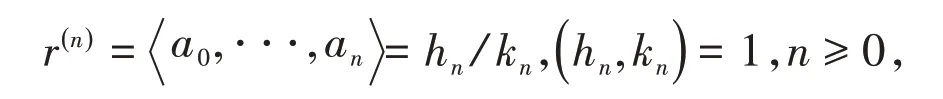
其中hn,kn由定义1给出.特别地,还有



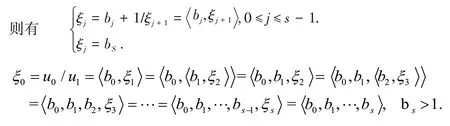
这就得到了ξ0=u0/u1的有限简单连分数表示式.由于bs≥2,得
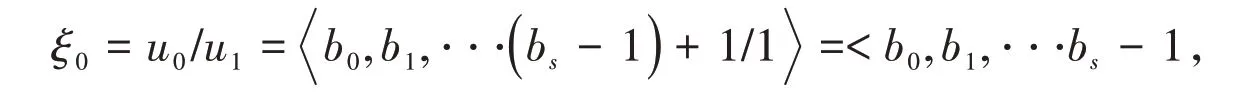
定理2设是个有限简单连分数,an>1,bs>1.若

证明:不妨设s≥n.对n用归纳法.当n=0时,若s≥1,则得
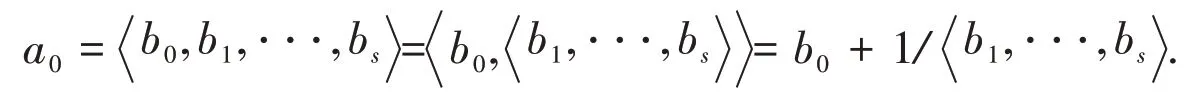
由于bs>1,所以,因此上式不可能成立.这就推出s=0,a0=b0.
所以结论当n=0时成立.假设当n=k(≥0)时结论成立.
当n=k+1时,注意到s≥n≥1,则

由归纳假设知,从上式就推得s=k+1及aj=bj,1≤j≤k+1.这就证明了当n=k+1时结论也成立.所以结论对一切n≥0都成立[1-3].
定理3(逼近原理)设d>1 不是平方数.若不定方程x2-dy2=±1 有解x=x0>0,y=y0>0.那么,一定是的某个渐近分数,且x0=h,y0=kn.
证明:由题意必有x0≥y0.否则从y0>x0可推出±1=x02-dy02<y02-dy02≤-y02≤-1.这是不可能的,由x0,y0是解及x0≥y0可得
逼近原理并未指出Pell 不定方程是否有解,但结论表明,我们只要在的渐近分数中去寻找到一个解,我们就可以探索出这类方程的某种解法,并求出方程的一般解.由此我们需要去研究的无限简单连分数表示式的性质,从而找出Pell 方程的解法,并更进一步了解其解的关系和构造[4].
2 两类Pell方程的解法及其解的构造
下面我们用连分数的逼近原理来探讨两类Pell方程的解法及其解的构造

这里d是非平方数,d>1,满足x>0,y>0 解称为正解.知道了方程的正解,很显然±x,±y均是方程的解,因此我们只需求出Pell方程的正解[1].
定理4设ξ0=,它的循环连分数周期为l,渐进分数为hn/kn.那么,
当l为偶数时,不定方程(2)无解,不定方程(1)的全体正解为

当l为奇数时,不定方程(2)的全部正解为
不定方程(1)的全部正解为

证明:若x,y是不定方程(1)或(2)的一组正解,那么必有某个n≥0使x=hn,y=kn.

当qj≠-1及当且仅当l|j时qj=1知仅当n+1=jl(j>0)时,hn=hlj-1,kn=klj-1才有可能是不定方程(1)或(2)的解,这时,j>0.由此就推出方程的全部解.由于当x,y是不定方程(1)或(2)的解时,±x,±y(正、负号任意选取)也是不定方程(1)或(2)的解,再注意到±1,0是(1)的解,及h-1=1,k-1=0,从定理4立即得到如下推论.
推论1在定理4的符号和条件下,
当l为偶数时,不定方程(2)无解,不定方程(1)的全部解为

其中正、负号任意选取.
当l为奇数时,不定方程(2)的全部解为

不定方程(1)的全部解为

以上正、负号均为任意选取.
定理4 表明,为了求出不定方程(1)和(2)的全部正解,就要去求出的所有渐进分数hlj-1/klj-1(j=1,2,⋅⋅⋅).当然逐个去求不仅麻烦也是不可能的.下面将证明只要求出hl-1,kl-1,利用解与解之间的关系,其他的解都可用它表示出来,这种解的构造可以求出Pell 方程的通解,一般的,当x,y是不定方程(1)或(2)的正解时,我们就说二次无理数x+是不定方程(1)或(2)的正解[4].
定理5设ξ0=,它的循环连分数的周期为l,渐近分数为hn/kn(n≥0),那么有
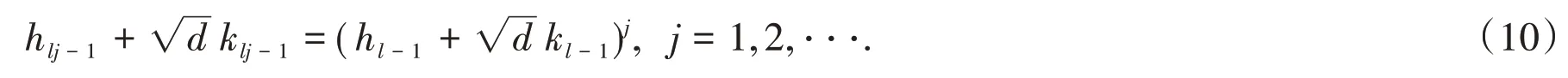
证明:记pj=hlj-1+,它的共轭数.
定理4证明了不定方程(1)和(2)(有解的话)的全部正解由pj(j≥1)给出,易证

因此,对任意j>1,必有正整数k满足.

为了证明式(10),只要证明必有k=j.显见,所有一定不是方程(1)或(2)的正解.由此及定理1 和式(13)就证明了和pj(j≥1)一样,都分别给出了不定方程(1)和(2)的全部正解,因此,这两个集合是一样的.注意到(利用式(12)及p1>1)

所以式(13)成立[5].
推论2在定理4的符号和条件下,
当l为偶数时,不定方程(2)无解,不定方程(1)的全部解为

其中正、负号任意选取.
当l为奇数时,不定方程(2)的全部解为

不定方程(1)的全部解为

以上正负号均为任意选取【4】.显见{hl-1,kl-1}是正解中的最小的.如果(2)有解,我们把{hl-1,kl-1}及p1=hl-1+称为不定方程(2)的最小正解,{h2l-1,k2l-1}及p2=h2l-1+称为(1)的最小正解;如果(2)无解,称{hl-1,kl-1},及p1为(1)的最小正解[1,6].
例1 求不定方程

其周期为12,根据推论2可知,不定方程(20)无解.
不定方程(19)的最小正解是x=h11,y=k11,

由此得(19)全部解为x+,j=0,1,2,3,4,⋅⋅⋅.
例2 求不定方程
其周期为11,不定方程(21)的最小正解是x=h10,y=k10,

根据推论2可知,不定方程(21)的解为:

不定方程(22)的解为:

3 结束语
本文从有限简单连分数的性质及其与有理分数的关系出发,巧用有限简单连分数的独特性质,用逼近原理来探讨两类Pell 方程的解法及其解的关系,从理论上阐述了用逼近原理解Pell 方程的有效性,这种解法还可以为破解RSA公钥密码提供很大的帮助[7].

