LEDA：一种基于Levenshtein距离的DNA序列拼接算法

崔竞松，薛 慧，王兰兰，郭 迟

1.空天信息安全与可信计算教育部重点实验室，武汉大学国家网络安全学院，湖北武汉 430072；

2.河海大学 理学院，江苏 南京 211100；

3.武汉大学卫星导航定位研究中心，湖北武汉430079

0 引言

DNA测序技术是指在给定的基因组中确定碱基序列排列方式，碱基序列包括腺嘌呤（A）、胸腺嘧啶（T）、胞嘧啶（C）与鸟嘌呤（G）。两条核苷酸序列配对构成DNA序列，其中每一对碱基A与T、G与C构成碱基对（base pair，bp）［1］。DNA测序技术是生物学家们了解DNA结构的重要技术手段。

目前的测序技术大致可以分为三代。第一代测序技术——传统的Sanger测序［2］，早在1977年被提出。该测序技术能够产生长度约为1 000的读段，且测序错误率极低，范围在0.001%～0.01%，但是Sanger测序成本高，速度慢，应用范围受到限制。因此，自2005年以来，大量的第二代测序技术被提出，第二代测序技术通常也被称为下一代测序技术［3］（next-generation sequencing，NGS）。与第一代Sanger测序相比，下一代测序技术成本较低，可以在较短的时间内对大量的DNA序列片段同时测序，而且其测序错误率也比较低，为0.5%～1.0%。但是，下一代测序技术产生的读段长度较短，一般仅包含75到300个碱基。因此，为了解决下一代测序技术存在的读段长度较短的问题，第三代测序技术被提出，主要包括Single Mplecule Real Time Sequencing［4］和Oxford Nanopore［5］。第 三代测序技术能够产生包含超过10 000个碱基的读段，但是测序错误率过高，在10%～15%，远远高于第一代测序技术和下一代测序技术。而且，第三代测序技术的测序成本也明显高于下一代测序技术。

由于下一代测序技术的低测序成本、低错误率和高通量等特性，目前该测序技术为市面上应用最为广泛的测序技术。由于受技术限制，下一代测序技术存在的问题是测序长度较短，随着读段长度的增长，测序错误率会急剧增加。为了解决这个问题，目前主流的下一代测序平台均采用双端测序技术（paired-end sequencing）［3，6］。双 端测序从DNA片段的两端分别开始测序，并生成高质量、可比对的测序数据。对于测序末端，由于测序长度过长而导致错误增加，可以根据另一条测序序列来进行纠正，因为此处位于另一条序列的前端，具有较低的测序错误率。相比于单端测序从DNA片段的一端开始测序，产生的每条读段（read）之间没有联系，双端测序技术在测序过程中是从待测序列片段的两端各测序一次。在测序过程中，测序的准确率会随着测序的进行而下降，即reads越往后面越不准确。双端测序产生的数据是成对出现的，每条read都有与其相匹配的另外一条read相对应。一般而言，双端测序的两条相对应的reads的尾部会有重叠区域，定义为overlap，将双端的reads进行比对可以拼接出更长的序列。对双端测序的reads进行拼接是对整个基因组的序列的分析的第一步，并且更长的reads会显著的提高基因组拼接质量，因此，它的准确性对所有下游分析都至关重要。

为了将双端测序产生的大量的reads拼接成更长的序列，已有一些拼接算法解决此问题，然而由于测序错误的存在，拼接仍然是一项有挑战性的工作。即使双端测序所得到的reads已经足够短了，比如常用的Illumina平台为150 bp，但在overlap区域仍然有一定的测序错误率。当overlap区域出现了测序错误时，将两条read拼接起来，便难以确定正确的overlap的区域；当read1和read2的overlap部分的碱基不匹配时，便难以确定哪个才是正确的。这给拼接造成了极大的困难。因此需要一种可以进行纠错的DNA序列拼接算法。常用的基于双端测序的拼接算法有Shera［7］、FLASH［8］、COPE［9］。Shera拼接时需要依赖fastq质量值，且其速度较差；FLASH算法正确率较高、速度比Shera快，但是在使用条件上，它同样依赖于fastq质量值且有最短的overlap长度要求，同时在拼接之前需要借助工具Bowtie［10］对reads进行纠错才能拼接；COPE需要利用kmer频率信息和fastq质量值去拼接，且具有较高的内存需求和相对较长的执行时间。这三种算法都是先遍历双端reads的每一个位点，寻找到合适长度的overlap，再通过测序质量值去处理重叠区域里不相同的碱基。由于read的长度一般为75～300 bp，所以时间代价往往比较大，且拼接效果依赖于测序质量值，而测序质量值在理论上来说只是一种概率性的值，往往并没有那么准确。因此从使用条件上来说，以上算法限制较多［11］。同时这些算法自身不具备纠错能力，纠错需要借助额外的工具［12］。

因此，为了解决现有的拼接算法在拼接时具有诸多限制条件，且拼接时间复杂度高的问题，本文在第二代测序技术的背景下，针对双端测序技术所产生的两条reads，充分利用两条reads尾部的重叠序列，将确定overlap长度问题与处理不匹配碱基问题相统一，即将拼接与纠错相结合，设计了一种基于Levenshtein距离的DNA序列拼接算法，简称LEDA算法。

1 Levenshtein距离

1.1 Levenshtein距离定义

Levenshtein距离即文本编辑距离，这一概念是由俄罗斯科学家Levenshtein于1965年提出的［13］，它用于两个字符串之间差异程度的量测，量测方式是计算至少需要多少次的操作才能将一个字符串变成另一个字符串。给定两个字符串A和B，将A转换成B所需要删除、插入等操作的集合就叫做A到B的编辑路径。其中最短的编辑路径就叫做字符串A和B的编辑距离。Levenshtein距离许可的编辑操作有：将一个字符替换（substitute，sub）成另一个字符，插入（insert，ins）一个字符，删除（delete，del）一个字符。

编辑距离的应用十分广泛。Unix下的diff及patch命令也是利用编辑距离来进行文本编辑对比。DNA可以视为由A、C、G和T组成的字符串，因此，编辑距离可判断两个DNA的类似程度。

由于DNA序列测序过程中可能发生的三种错误sub，ins，del和Levenshtein距离的三种编辑操作相同，因此本文选择Levenshtein距离设计相关算法。

1.2 Levenshtein距离求解原理

Levenshtein距离的求解采用动态规划的思想，其基本思想是将原问题转换为求解多个相似子问题，通过子问题的求解计算出原问题的解。在求解编辑距离时需要构建编辑距离矩阵，逐行求出矩阵中每个元素的值，最终得到矩阵中最后一个元素的值，该值即为两个字符串的编辑距离［14］。

设有两个字符串A和B：A=a1，a2，…，am，B=b1，b2，…，bn，其长度分别是m和n。首先建立A和B的规模(m+1)×(n+1)的编辑距离矩阵D。设字符串A的前i个字符所组成的子字符串为A[1～i]，字符串B的前j个字符所组成的子字符串为B[1～j]。定义矩阵D如下

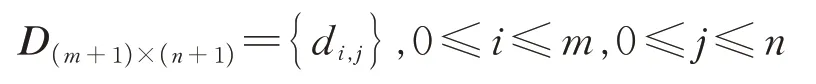
矩阵的每一个元素di，j表示字符串A的前i个字符组成的字符串A[1～i]和字符串B的前j个字符组成的字符串B[1～j]的编辑距离。我们可以对任意一个字符串A或B进行插入一个字符、删除一个字符、替换一个字符三种操作。因此对于两个字符串，共有六种操作方法。但其中，对字符串A删除一个字符和对字符串B插入一个字符是等价的，比如当A=“doge”，B=“dog”时，既可以删除A的最后一个字符e，得到相同的“dog”，也可以在B的末尾添加一个字符e，得到相同的“doge”；同理，对字符串B删除一个字符和对字符串A插入一个字符是等价的；对A替换一个字符和对B替换一个字符是等价的，比如当A=“bat”，B=“cat”时，修改A的第一个字符b为c，和修改B的第一个字符c为b是等价的。因此，本质上不同的操作只有在A中插入一个字符、在A中删除一个字符、替换A的一个字符这三种。

假设已知di-1，j-1，di-1，j，di，j-1的值，则可以计算出di，j的值。对于di，j的求解，分别考虑以下三种不同的操作：

1）插入：把B的第j个字符插入到A的第i-1个字符后。由于已知经过di-1，j次操作即可将A[1～i-1]转换为B[j]，因此把B的第j个字符插入到A串的第i-1个字符后，即可将A[1～i]转换为B[1～j]，此时di，j最小为di，j-1+1。

2）删除：把A的第i个字符删除。由于经过di，j-1次操作即可将A[1～i]转换为B[1～j-1]。因此把A的第i个字符删除，即可使A[1～i]和B[1～j]相等，此时di，j最小为di，j-1+1。

3）替换：把A的第i个字符替换为B的第j个字符。由于经过di-1，j-1次操作即可使A[1～i-1]和B[1～j-1]相等，此时把A的第i个字符替换为B的第j个字符，则可使A[1～i]和B[1～j]相等，此时di，j最小为di-1，j-1+1。特别地，若A的第i个字符和B的第j个字符原本就相同，则不需要进行替换操作，这种情况下，di，j最小可以为di-1，j-1。

对于边界情况，即对于矩阵D的第一行和第一列，表示一个空字符串和一个非空字符串相互转换的编辑距离，此时编辑距离为非空字符串的长度。

基于以上分析，得到求解编辑距离的公式如下

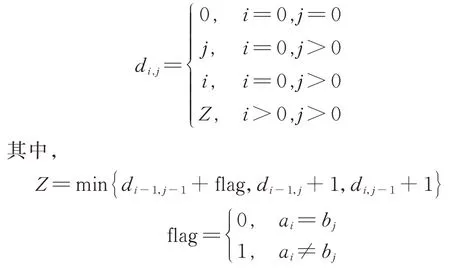
2 LEDA算法

将上述Levenshtein距离原理运用到DNA序列拼接中，原DNA序列overlap区域发生了插入和删除错误造成了overlap长度的变化，原DNA序列overlap区域发生了替换错误造成了overlap区域碱基的变化，即原DNA序列overlap区域发生了插入、删除和替换错误产生了overlap1和overlap2，将DNA序列拼接问题转化成原序列片段发生了插入、删除和替换三种错误生成的两条序列的字符串比对问题。通过将DNA序列拼接问题与编辑距离相结合，比对双端测序所产生的两条DNA序列片段overlap1和overlap2，得到overlap1与overlap2的编辑距离，在由一个序列转换成另一个序列的过程中，寻找所有可能正确的DNA序列片段，最后拼接成完整的DNA序列。

2.1 算法原理

本文所提出的LEDA算法是基于下一代测序技术所产生的读段。目前下一代测序技术采用的是深度测序（sequencing depth），即对基因组进行多次测序，有时可达数百次甚至数千次。下一代测序技术所测得reads长度一般为几十到几百bp。

测序仪完成DNA序列的测序后会产生一系列原始文件，称为fastq文件，该文件用于下一代测序数据的存储。本文所提出的拼接算法需要将测序后生成的原始的fastq文件中读入测序片段。通常，双端测序所产生的一对reads的序列的关系如图1所示。

图1 双端测序产生的一对reads序列Fig.1 A pair of reads generated by DNA paired-end sequencing

Read1和Read2的尾部会有overlap序列，可截取得到双端的overlap序列，分别为overlap1和overlap2，其长度相等。如果在DNA序列没有产生错误的情况下，overlap1和overlap2应该与5-3正序overlap相同。如果overlap1和overlap2不相同，则说明DNA序列合成或者测序过程中产生了错误，可能是overlap1和overlap2都发生了替换/删除/插入错误或其中一段无错，另一段发生了替换/删除/插入错误。

2.2 算法流程

设

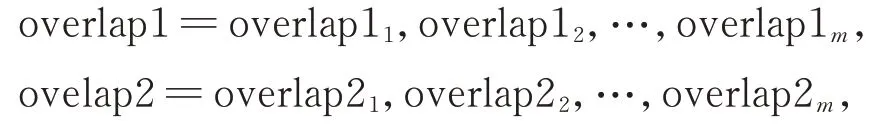
其长度均为m。设序列overlap1的前i个碱基所组成的子序列为overlap1[1～i]，序列overlap2的前j个碱基所组成的子序列为overlap2[1～j]。

2.2.1 构造编辑距离矩阵min_ed

通过动态规划的思想构造overlap1和overlap2的阶为(m+1)×(m+1)的编辑距离矩阵min_ed。定义矩阵min_ed为：

矩阵中的每一个元素min_edi，j代表从overlap1[1～i]变换至overlap2[1～j]所需要的最少变换次数。

矩阵min_ed的构造方法如下：

1）矩阵的第0行第j列，代表由‘’变换到overlap2[1～j]，需要经过j次插入碱基的操作，共需要插入j个碱基。即min_ed0，j=j，‘’代表空碱基序列；

2）矩阵的第i行第0列，代表由overlap1[1～i]变换到‘’，需要经过i次删除碱基的操作，共需要删除i个碱基，即min_edi，0=i；

3）矩阵的第i行第j列，代表由overlap1[1～i]变换到overlap1[1～j]，需要经过的操作次数为min_edi-1，j+flag、min_edi，j-1+flag、min_edi-1，j-1三者中的最小值。其中，当且仅当overlap1i和overlap2j相等时，flag为1；否则，flag为0。

根据以上步骤得到矩阵min_ed，若min_edi，j=0，则说明overlap区域未发生任何错误，因此直接跳转到2.2.4节的步骤进行序列拼接。

2.2.2 构造编辑路径矩阵op

利用动态规划的思想构造overlap1和overlap2的阶为(m+1)×(m+1)的编辑路径矩阵op。矩阵op定义如下

矩阵op中的每一个元素opi，j为一个集合，代表从overlap1[1～i]变换到overlap2[1～j]共有in_op1，in_op2，…，in_opu一共u种不同的编辑路径，即

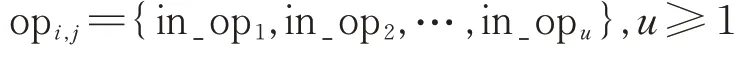
其中每一条编辑路径in_op代表将overlap1[1～i]变换到overlap2[1～j]的v次操作，in_op={error_correct1,error_correct2,…,error_correctv},v≥1其中每一个元素error_correcti代表一项具体的操作，可能是无错/替换/删除/插入，即

其中，‘0’代表无错操作，‘1’代表替换操作，‘2’代表删除操作，‘3’代表插入操作。

矩阵op的构造需要采用动态规划的思想逐行求出矩阵中每个元素的值，op由矩阵min_ed以及overlap1和overlap2共同决定，其具体构造方法如下：

1）矩阵op的第0行第j列，表示从空碱基序列转换到非空碱基序列的编辑路径，此时只有一种编辑路径，即op0，j={‘{3’，‘3’，…，‘3’}}，一共j个‘3’。

2）矩阵op的第i行第0列，表示将一个非空碱基序列转换为空碱基序列的编辑路径，此时只有一种编辑路径，即opi，0={‘{2’‘，2’，…，‘2’}}，一共i个‘2’。

3）矩阵的第i行第j列，此时已知opi-1，j，opi，j-1，opi-1，j-1的值，则可以求出opi，j的值，opi，j的求解需要先考虑overlap1i与overlap2j是否相同：

①若overlap1i=overlap2j，则将opi-1，j-1里包含的所有的集合均添加一个无错操作（操作‘0’）后，添加到opi，j中；

②若overlap1i≠overlap2j，则将opi-1，j-1里包含的所有的集合均添加一个替换操作（操作‘1’）后，添加到opi，j中；

接着分别考虑min_edi-1，j和min_edi，j-1是否等于min_edi，j+1：

①若min_edi，j=min_edi-1，j+1，则将opi-1，j里包含的所有的集合均添加一个删除操作（操作‘2’）后，添加到opi，j中；

②若min_edi，j=min_edi，j-1+1，则将opi，j-1里包含的所有的集合均添加一个插入操作（操作‘3’）后，添加到opi，j中。

2.2.3 纠错恢复正确的overlap序列t

利用矩阵op的最后一个元素opm，m去纠错恢复正确的overlap序列，t表示原始的正确的overlap序列，t的构造方式如下：

已 知opm，m={in_op1，in_op2，…，in_opu}，遍 历其中的每一个元素in_op，进行如下操作：

1）初始化t为空碱基序列，即t=‘’。

2）已知in_op={error_correct1，error_correct2，…，error_correctv}，v≥1，遍历其中的每一个元素error_correcti(1≤i≤v)：

①若error_correcti为‘0’，说 明overlap1i和overlap2i相同，无需进行纠错，将overlap1i添加到碱基序列t中。

②若error_correcti为‘1’，说 明overlap1i或overlap2i在此处产生了sub错，在此处可能是overlap1i正确或者是overlap2i正确，因此将overlap1i或者是将overlap2i添加到t中。

③若error_correcti为‘2’，说明可能是overlap1i在此处发生了ins错添加了一个碱基，或者是overlap2i在此处发生了del错删除了一个碱基。此时将overlap1的长度减1，或将overlap1i添加到t。

④若error_correcti为‘3’，说明可能是overlap1i在此处发生了del错删除了一个碱基，或者是overlap2i在此处发生了ins错添加了一个碱基。此时将overlap2i添加到t中，或将overlap2的长度减1。

每一步操作后便进入一次递归，直至穷举完所有可能的情况。当遍历完in_op的所有元素时，便将此时的t添加到结果集中。

上述操作如图2所示。

图2 基于op m,m寻找所有可能正确序列的流程图Fig.2 The flow chart based on op m,m to find all possible correct sequences

3）当遍历完opm，m的所有元素时，即可得到所有可能正确的原始的overlap序列。

2.2.4 拼接

将所有可能正确的DNA序列片段t与app1、app2拼接，其中，app1是Read1剩下的序列片段，app2是Read2剩下的序列片段经过图3所示的操作后得到的序列片段。如图3所示。

图3 DNA序列拼接Fig.3 DNA sequence assembling

2.3 算法伪代码

上述2.2节LEDA算法流程的伪代码如算法1所示。

3 实验部分

为了验证本文的研究成果，我们做了仿真数据实验与真实数据实验，在仿真数据实验中从改变错误类型与改变错误数量两个维度进行实验，以评估本文所提出的拼接算法的纠错能力。在真实数据实验中，主要通过拼接正确率和时间复杂度评估本算法的可行性。

3.1 仿真数据实验

3.1.1 实验环境

操作系统Windows10 64位，处理器Intel（R）Core（TM）i5-10400 CPU@2.90 GHz 2.90 GHz，RAM 16.00 GB，编译环境Python3.7。

3.1.2 结果及分析

仿真实验中，我们从改变错误类型以及改变错误数量两个方面设计实验，以分析LEDA算法对于测序出错的序列的拼接与纠错能力。本文构造了20 000条含有200个碱基对的随机DNA序列作为仿真实验的DNA模板链，然后模拟下一代测序技术生成20 000对reads。对正确的reads进行注错测试，然后用LEDA算法进行拼接，将拼接后的序列与原先正确的DNA模板序列进行比对以检验算法的拼接正确率以及纠错能力。

由于在双端测序的过程中，越接近测序序列的尾部出错率越高，且本文所设计的算法仅对于overlap部分的序列有纠错能力，所以实验中对序列注错的位置均在overlap部分。在实验中，将无错操作看作特殊的替换，即替换为自身。

1）错误类型的影响

对于Read1和Read2的overlap部分的序列分别进行1个错的随机注错测试，分6种不同错误类型讨论，见表1。

由于DNA双链的互补与对称性，6种分类对于Read1与Read2的顺序没有要求，因此无需交换Read1与Read2的顺序再次实验。

本实验计算了在6种不同错误类型、错误发生位置随机且错误数量不超过两个的情况下，20 000条含有200个碱基对的随机DNA序列利用该算法拼接的正确率以及运行时间。测试结果如表1。

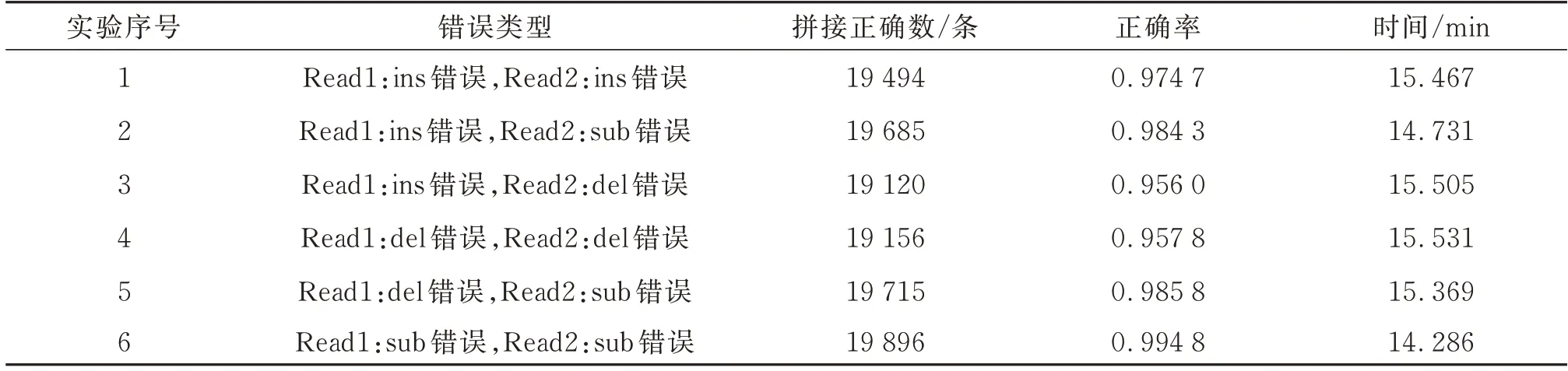
表1 不同错误类型DNA序列拼接正确率和时间Table 1 DNA sequence assembly success rate and time with different error types

分析结果可得，上述条件下的随机DNA序列拼接平均正确率为0.975 6，平均运行时间为15.148 min，平均每对reads拼接所用时间为45.444 ms。由此可得本文算法可以处理各种类型的错误，拼接高效且正确率高。

2）错误数量的影响

对于Read1和Read2的overlap部分的序列分别进行错误数量为1、2、3、4个错误的随机注错测试。

本实验计算了错误数量从1增加到4的情况下，20 000条含有200个碱基对的随机DNA序列利用本文算法拼接的正确率以及运行时间。测试结果如表2。

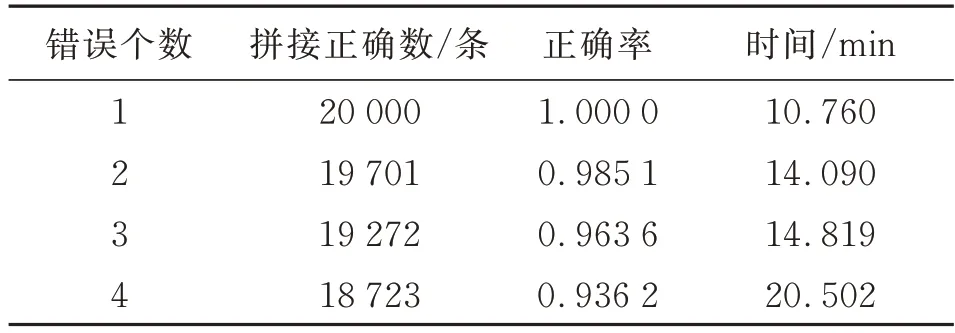
表2 不同错误个数DNA序列拼接正确率和时间Table 2 DNA sequence assembly correct rate and time of differ ent number of err ors

分析结果可得，上述条件下DNA序列拼接平均正确率为0.971 2，平均运行时间为15.043 min，平均每对reads拼接所用时间为45.129 ms。20 000条含有200个碱基对的随机DNA序列拼接正确率随着错误数量的增加而下降，但仍在可以接受的范围，因为考虑到下一代测序错误率仅为0.5%～1.0%，对于实验读段长度为150，错误个数不超过1.5个，可见LEDA算法完全可以应对实际测序中所出现的错误，在实际应用中性能较好。

3.2 真实数据实验

为了验证本文所述算法在实际应用中的有效性，我们不仅做了仿真实验，而且也做了真实的测序实验。真实的测序数据由二代测序的Illumina的Hiseq4000测序平台测序所得，测序文库是一个有11 520条长度为180 nt（nt即核苷酸）DNA的文库，其reads长度为150 nt，为双端读段，所有的Read1和Read2分别由两个fastq文件存储。Read1和Read2分别有5 003 753条，大小共为3.36 GB。实验环境与3.1节仿真实验环境相同。

3.2.1 实验过程

1）数据处理

①处理fastq文件，读取其中的Read1和Read2，并分别存储在不同的列表Read1和Read2里。

②考虑到第二代测序的错误率很低，仅为0.5%～1.0%，对于实验中读段长度为150，错误个数大都不超过2个，而且下一代测序采用的是深度测序，对于本实验其平均测序深度约为434，即平均每个碱基都会被测序434次。因此，实验中筛选出Read1与Read2尾部重叠部分即overlap1与overlap2的编辑距离小于等于1的序列，得到3 928 926对Read1和Read2序列，占总序列78.52%。

③为了确保实验的可靠性，我们也从实验中筛选出Read1与Read2尾部重叠部分即overlap1与overlap2的编辑距离小于等于2的序列，最终得到4 459 805对Read1和Read2序列，占总序列的89.13%。

可见，编辑距离控制在1或2以内，便可以涵盖fastq文件中的大部分的数据，且由于二代测序的深度测序特性，即对于同一段序列可能会测出好几百倍甚至几千倍的结果，能够保证筛选出来的序列可以覆盖原始序列的所有碱基。

2）程序运行

①输入FASTQ文件处理后产生的两个列表Read1和Read2。

②由于有四种不同的引物，分别为模板链两端原本的引物以及两端原本引物的反向互补序列。引物不同会造成Read1与Read2拼接的方式会有所不同，所以实验中需要先判断Read1的引物类型，然后再分类型讨论返回结果。

③将运行得到的所有可能正确的DNA序列与测序文库比较，检验算法拼接正确率。

3.2.2 实验结果

测序文库中模板DNA序列共有11 520条，对于编辑距离小于等于1的reads，其拼接结果可以成功比对其中11 519条，即几乎可以拼接得到原来文库中的所有DNA序列，正确率为0.999 9，其总运行时间为2 393.809 6 min，平均每对reads拼接所用时间为36.56 ms。

为了保证实验的可靠性，我们也拼接了编辑距离小于等于2的Reads，其拼接结果也为11 519条，与编辑距离控制在1的拼接结果是相同的。

4 讨论

为了能更好地分析对比LEDA算法的拼接效果，我们将Shera、FLASH、COPE算法在3.2节中真实数据上运行，4种算法结果如表3所示。

从表3中可以看出，在使用条件上，LEDA算法无任何限制，而Shera算法需要fastq文件中质量值的信息，FLASH算法不仅需要fastq文件中质量值的信息并且在拼接之前必须要使用额外的纠错工具Bowite对reads进行错误纠正以提高拼接正确率，COPE算法需要fastq文件中质量值的信息以及k-mer频率信息对reads进行错误纠正。

表3 不同算法的使用条件、运行时间、时间复杂度以及拼接正确率Table 3 Use conditions、running time、time complexity and assembly correct rate of different algorithms

在正确率相同均为99.99%的情况下，LEDA算法平均每对reads拼接所用的时间比Shera、FLASH、COPE算法都要短。这是由于相比于其他拼接算法的时间复杂度与read的长度呈二次方的时间复杂度，LEDA算法与read长度并无直接关系，而是与overlap长度和编辑距离有关，时间复杂度为O（n·2x）。而实际情况中read的长度都大于overlap长度，且编辑距离都比较小，因此本算法的时间复杂度优于其他三种算法。

5 结语

相比于其他的一些DNA序列拼接算法，需要遍历Read1和Read2的所有可能组合的位点寻找所有可能的overlap，复杂且代价比较大，且使用时有诸多限制条件，本文提出的LEDA算法，将问题转化为原序列的overlap片段发生了ins、del和sub三种错误生成两条序列的字符串比对，拼接与纠错相结合，使用本文算法时不需要依赖其他任何工具做任何预处理工作，且对于overlap长度没有限制，不需要额外读段信息。在实际应用中使用简单且运行高效。在DNA序列拼接方面首次引入了Levenshtein距离的思想，不依赖于额外的信息，大大简化了已有的拼接算法依靠测序质量值等其他测序信息计算概率进行拼接的思路，LEDA算法本身就具备一定的纠错能力。

目前LEDA算法仅仅只能针对双端测序，无法适用于单端测序技术。另外，LEDA算法的高效是建立在需要严格控制overlap1和overlap2的编辑距离的基础上。LEDA算法无法解决整个基因组的拼接问题，只能解决基础的双端测序的拼接问题。未来，我们将继续探索将LEDA算法扩展，使其能用于整个基因组的拼接之中。