图基BCJ关系的弦论导出

柳景沛，杜一剑

武汉大学物理科学与技术学院，湖北武汉430072

0 引言

近年来研究表明，杨-米尔斯理论树级色排序散射振幅满足非平庸的Bern-Carrasco-Johansson（BCJ）关系［1］，这与早期发现的Kleiss-Kuij（f KK）关系［2］一起对树级色排序振幅的计算起到化简作用。近期对爱因斯坦-杨-米尔斯理论振幅递推展开公式［3～5］的研究引出了杨-米尔斯理论树级色排序振幅的图基BCJ关系。由于已有的KK和BCJ关系可以由弦论振幅关系的场论极限给出［6］，而场论中的图基BCJ关系是已有BCJ关系的组合［7］，因此我们期望通过适当组合弦论散射振幅，导出场论中的图基BCJ关系。

本文从具体例子出发，借助弦论中的KK和BCJ关系，找到弦论振幅满足的图基关系。这一关系在场论极限下给出了杨-米尔斯场振幅的图基BCJ关系以及与其伴随的图基KK关系。

1 已知的弦论与场论散射振幅关系

树级色排序杨-米尔斯场散射振幅满足以下的KK关系［2］

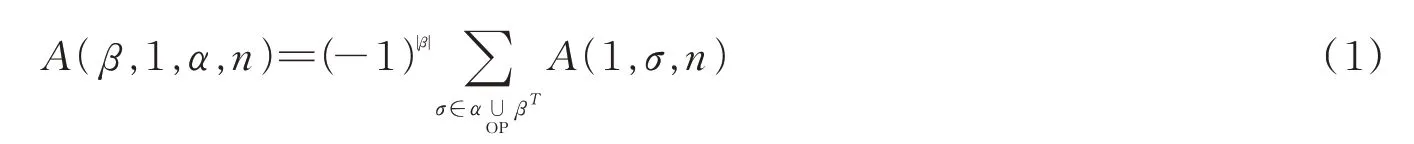
其中，A(1，σ，n)表示给定排序(1，σ，n)下的杨-米尔斯场散射振幅；α，β是给定的粒子排序；βT表示β中粒子排序的逆序；符号表示两个有序集的有序并集，在这个并集中每个有序集中元素保持原来的相对顺序。杨-米尔斯场树级色排序振幅还满足以下BCJ关系

（2）式左边定义为

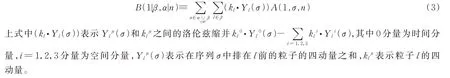
在弦论中，开弦树级散射振幅满足如下关系［1，8］

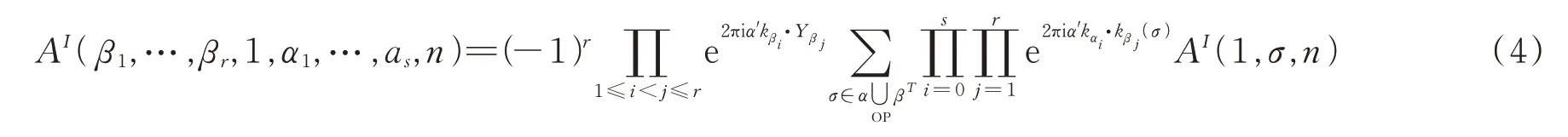
AI表示相应色排序的开弦散射振幅。当考虑外线为开弦无质量态并取场论极限α'→0后，（4）式左右两边的实部相等，所以可推出（1）中的KK关系，等式右边虚部为零则（2）式成立。因此，场论中的KK和BCJ关系可视为弦论中对应关系的近似。

文献［5］提出了如下图基BCJ关系

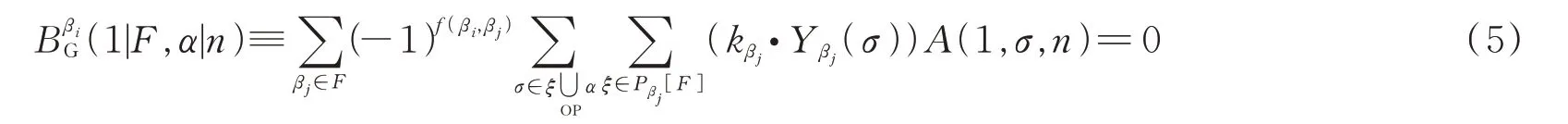
其中，F表示由点和线构成的树图；βi是任意选定的图中的一个点，称为基点；f(βi，βj)表示图中βi与βj的距离，即图中两点相隔的最短路线的线段数表示一个排序的集合，其中元素的排序由下列规则确定：1）βi在排序最左边；2）任意相邻两点与βi距离较近的排在左边；3）当两个分支连在同一点上时，可能的排序集合为各自分支排序的有序并集。这里以一个四点图作为例子，如图1所示，图中的点表示一部分外粒子。

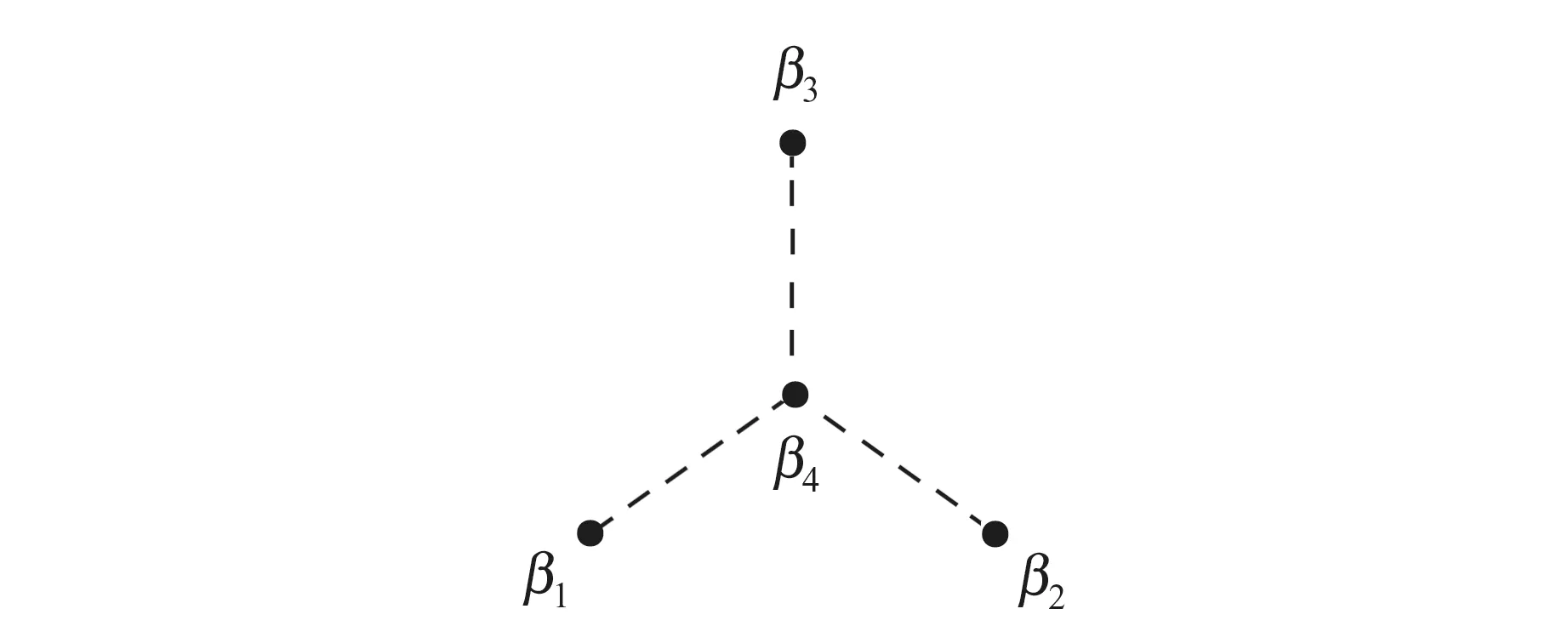
图1 四点图F4的一种情况Fig.1 A case of four-point graph F4

对应图1的表达式为

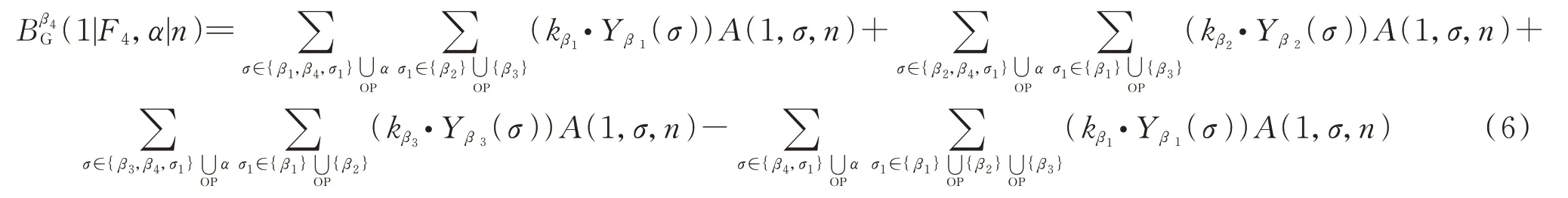
文献［7］证明了图基BCJ关系等号左边的式子可以表示为（2）式左边项的组合。于是可以证明有如下的图BCJ关系

本文给出弦论中的图基散射振幅关系，这些关系在场论极限下可以导出相应的杨·米尔斯场图基BCJ关系（5）。

2 少点弦散射振幅图基关系及与场论的对应

通过整合弦论振幅关系，计算两点、三点和一个四点的图基BCJ关系。这一计算方法可以推广至任意形式的图基BCJ关系。

对于杨-米尔斯场理论，单点的图基BCJ关系（5）会退化到一般BCJ关系（2）。因此，只需使用与文献［6］中相同的方法，便可得到最终结果，同时得到相应的KK关系。在这里，可以看见弦散射振幅的BCJ及KK关系与场论的BCJ及KK关系有着一一对应的关系。后面可以看到，证明高点的图基BCJ关系依赖于低点的这种对应。

先考虑两点图情况的弦论散射振幅关系，也就是选取β1为基点，且（5）式中F取图2的情况。

图2 两点图F2Fig.2 Two-point graph F2

为了找到与此情况对应的弦论中的关系，考虑如下的弦散射振幅组合

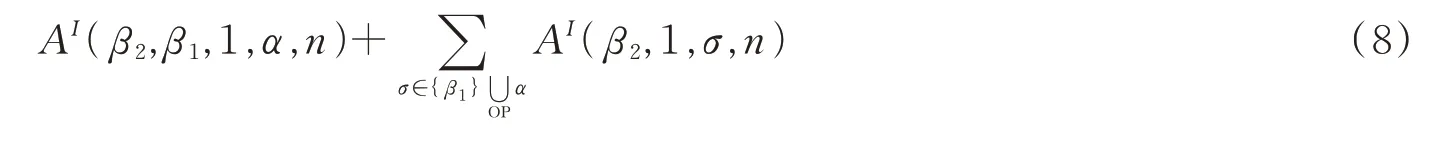
为了表示方便，有如下简记

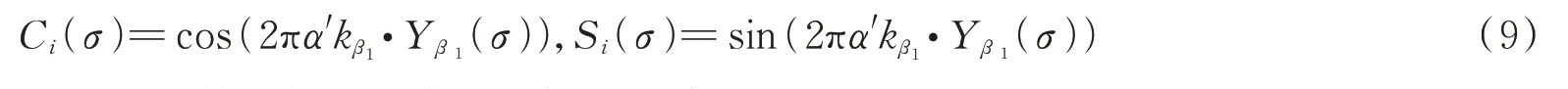
对于（8）式中的第一项，可以同样利用（4）式写成如下的关系

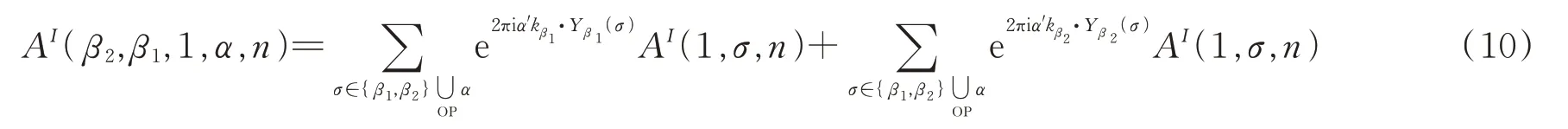
同理，对于（8）式第二项有

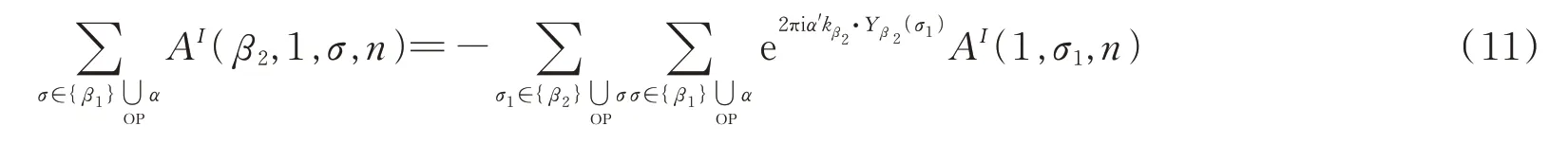
组合后取（8）式的虚部，因为式子是散射振幅的组合，其应该是实数，故虚部应为0，即

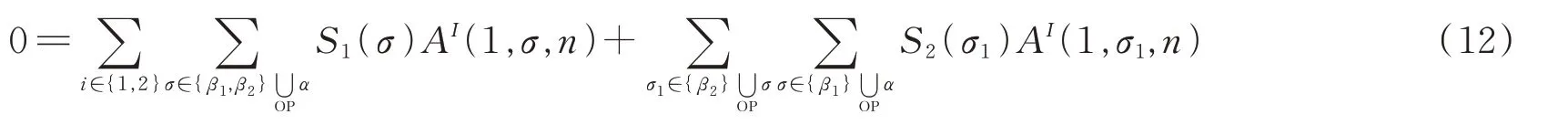
考虑（8）式的实部有如下关系

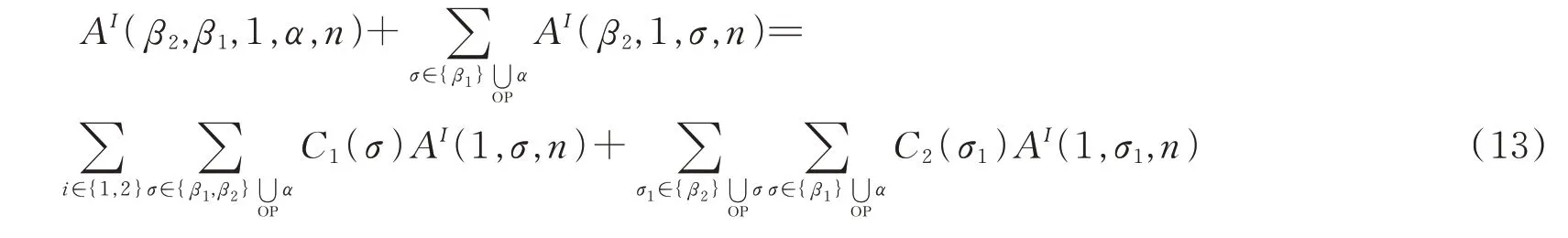
这两个关系就是弦散射振幅的图基BCJ和KK关系。在场论极限α'→0下，（13）式变为

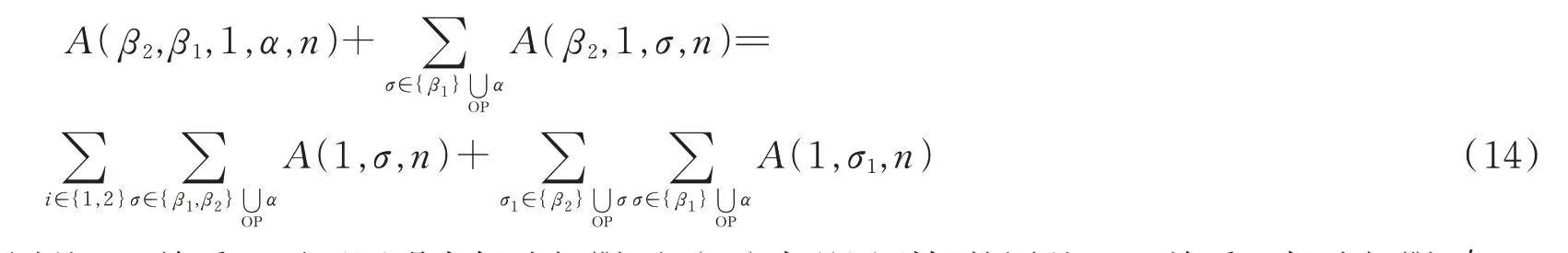
（14）式就是相应的图基KK关系。下面证明在场论极限下，（12）式退回到场的图基BCJ关系。场论极限α'→0下，（12）式可写为

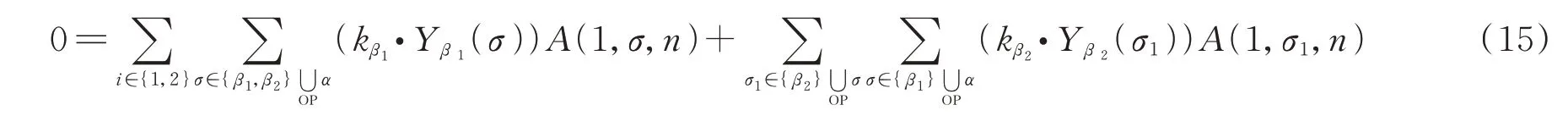
（15）式等号左边的第二项和（12）式第一项中i=2的项相加，可以得到

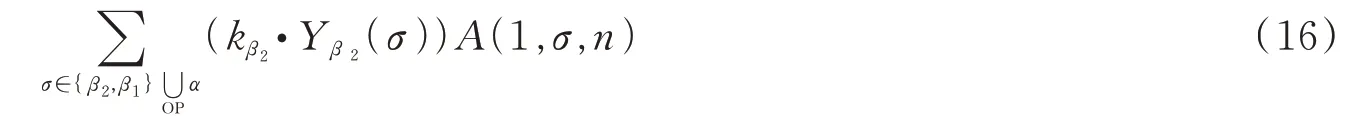
可以看到（16）式和（15）式第一项i=1的组合，正是杨-米尔斯场两点图基BCJ关系等式的右边。由此印证了弦散射振幅与杨-米尔斯场之间的对应关系。

弦散射振幅在三点图的情况下有两种不同的形式，但是它们对应着场论中的同一个关系。下面考虑三点图的弦论散射振幅关系，也就是定义式（5）中F取图3时的情况。

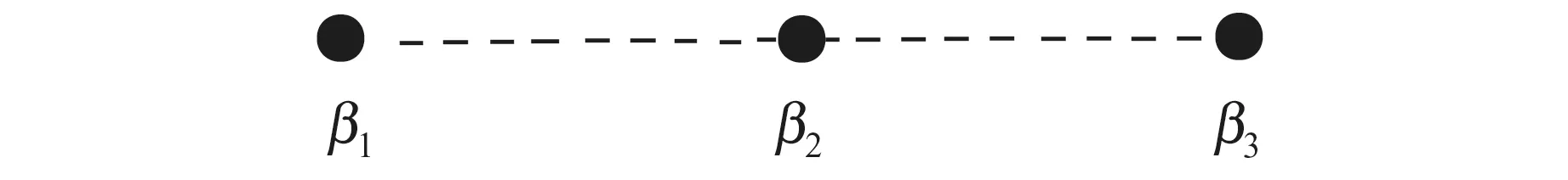
图3 三点图F3Fig.3 T hree-point graph F3

我们首先考虑选取β1为基点。

考虑如下的弦散射振幅组合

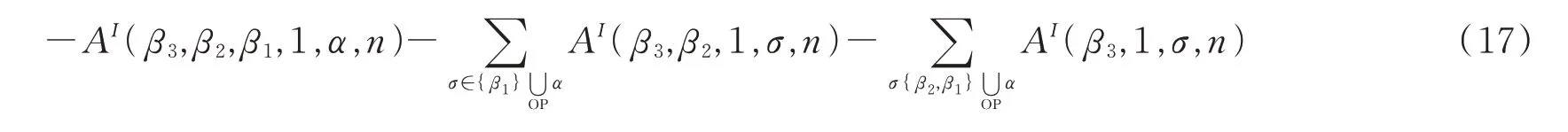
对（17）式中的第一项，利用（4）式的规则写成如下的关系

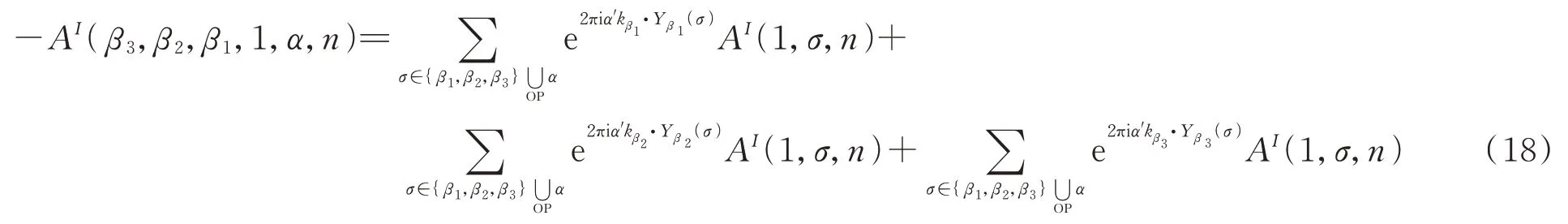
同理，对（17）式第二项有

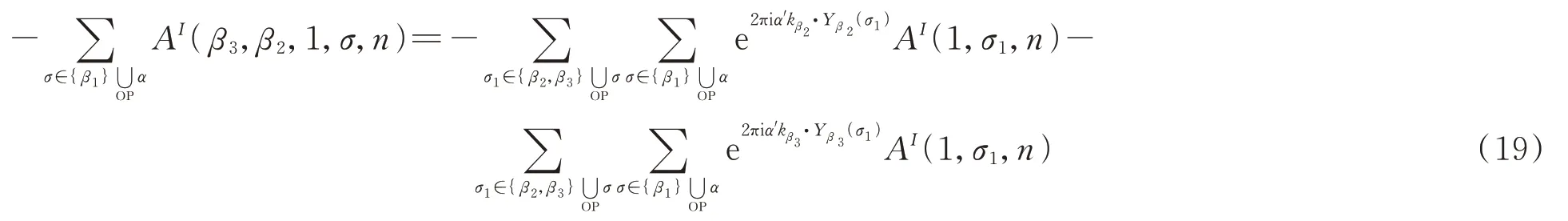
对（17）式第三项有

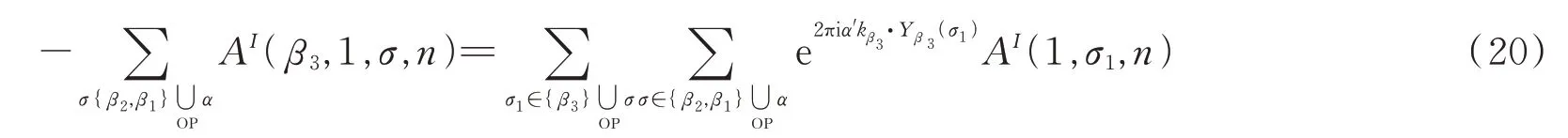
组合后，由于（17）式是散射振幅的组合，故虚部为0，得到如下关系

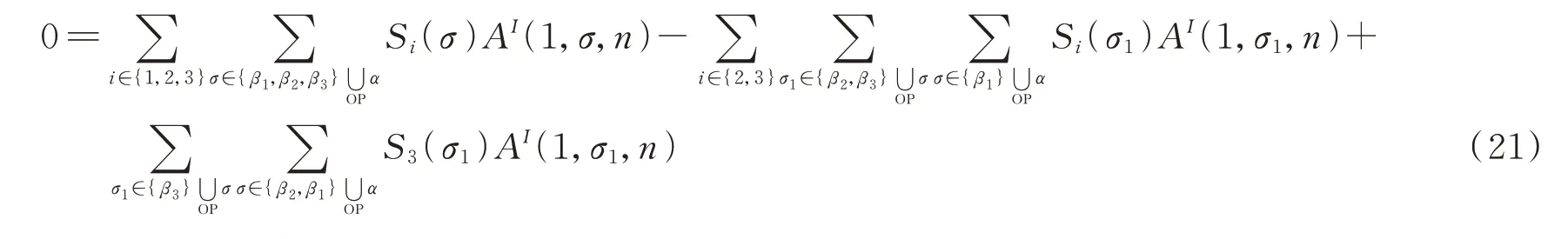
再取（17）式的实部，得到如下等式

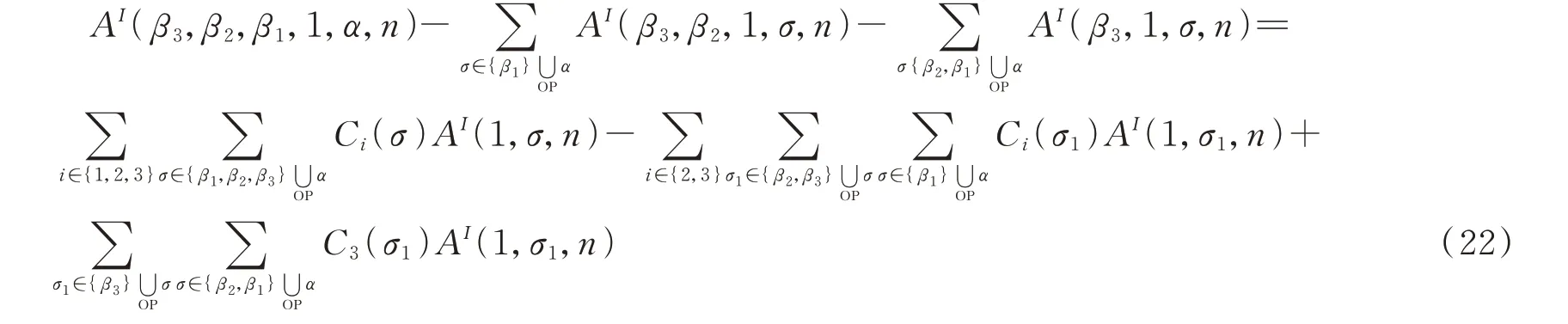
这两个关系就是弦散射振幅的图基BCJ和KK关系。在场论极限下，（22）式变为

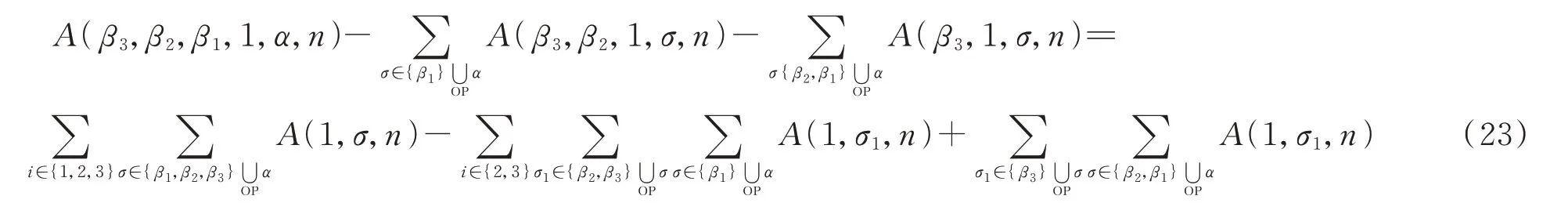
下面证明在场论极限下，（21）式退回到场的图基BCJ关系。场论极限下（21）式可写为

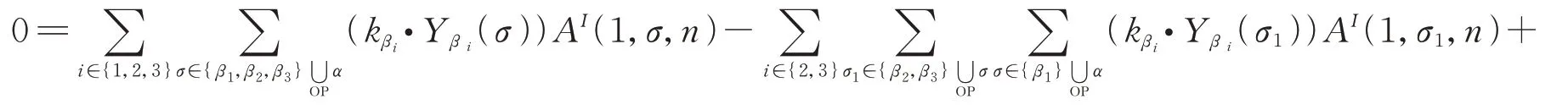
联系之前写出的BCJ关系式，（24）式中的第一项中i=2，3的部分可以记作

（25）式中B的定义与（3）式中的定义相同，β1≺β2表示只包含在色排序中β1排在β2的左边的那些项。（25）式和（24）式中的第二项结合得到

（26）式再与（24）式的最后一项合并，可以得到

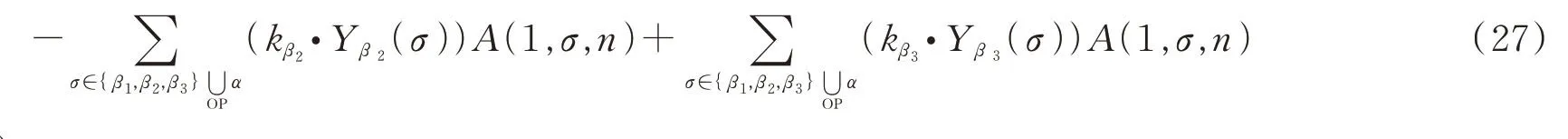
对（27）式和（24）式的第一项求和，可以看到这正是三点的图基BCJ关系。三点图还有另一种情况，即依旧使用图3，但以其中的中间点β2为基点。此时考虑如下的弦振幅组合

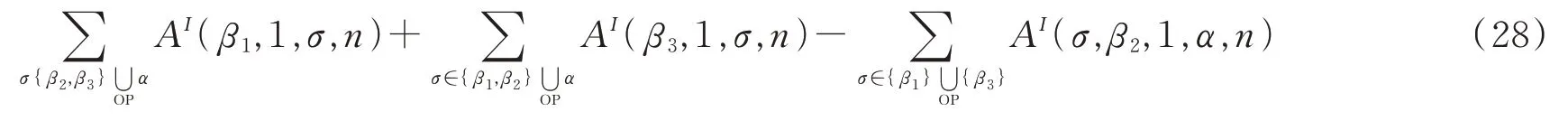
运用同样的方法可以得到

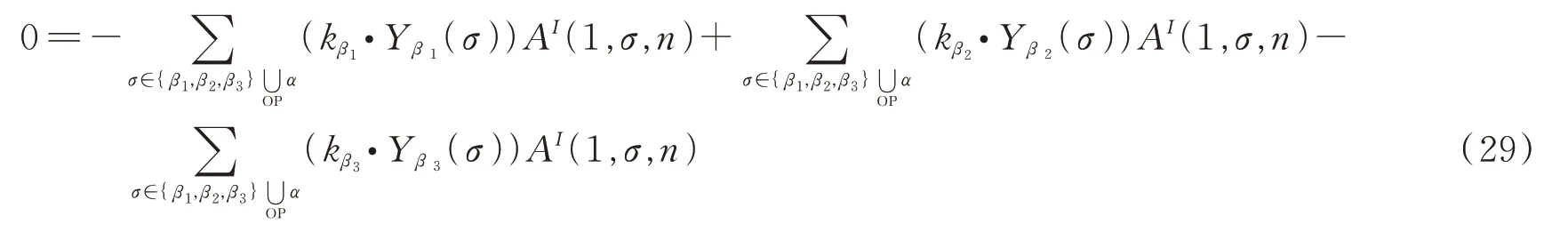
这也是三点的图基BCJ关系，只是基点不相同，因此与前一种方法得到的结果是相符合的。

考虑四点图的弦论散射振幅关系。对于四点图的散射振幅，也有多种不同情况，这里只重点计算最非平凡和有代表性的例子。考察定义式（5）中F如图1所示，以β4为基点的情况。考虑如下的弦散射振幅组合

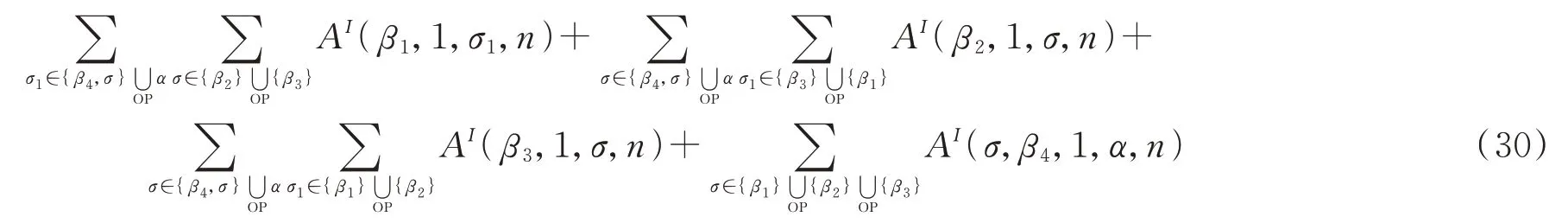
对（30）式中的第一项，同样利用公式（4）的规则写成如下的关系

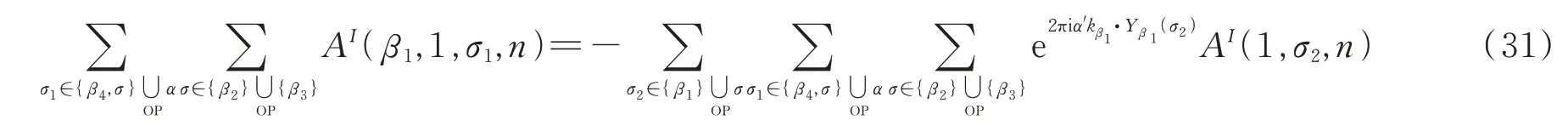
同理，对（30）式第二项有

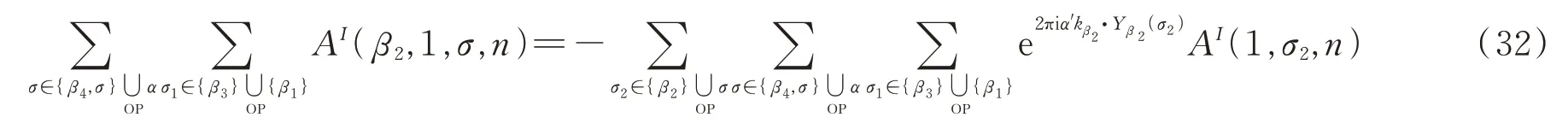
对（30）式第三项有

对（30）式第四项有

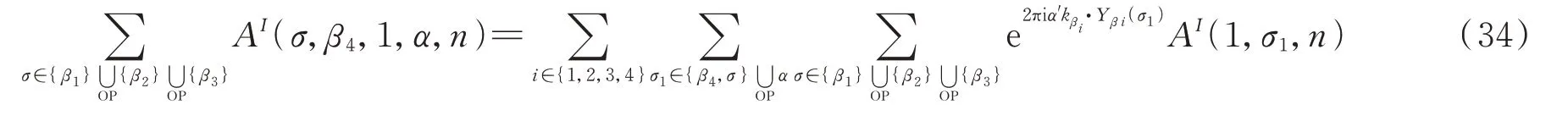
与前面同样的理由，等式（31）～（34）两边求和后式子的虚部为0，得到如下的关系

（31）～（34）式的实部相等，有

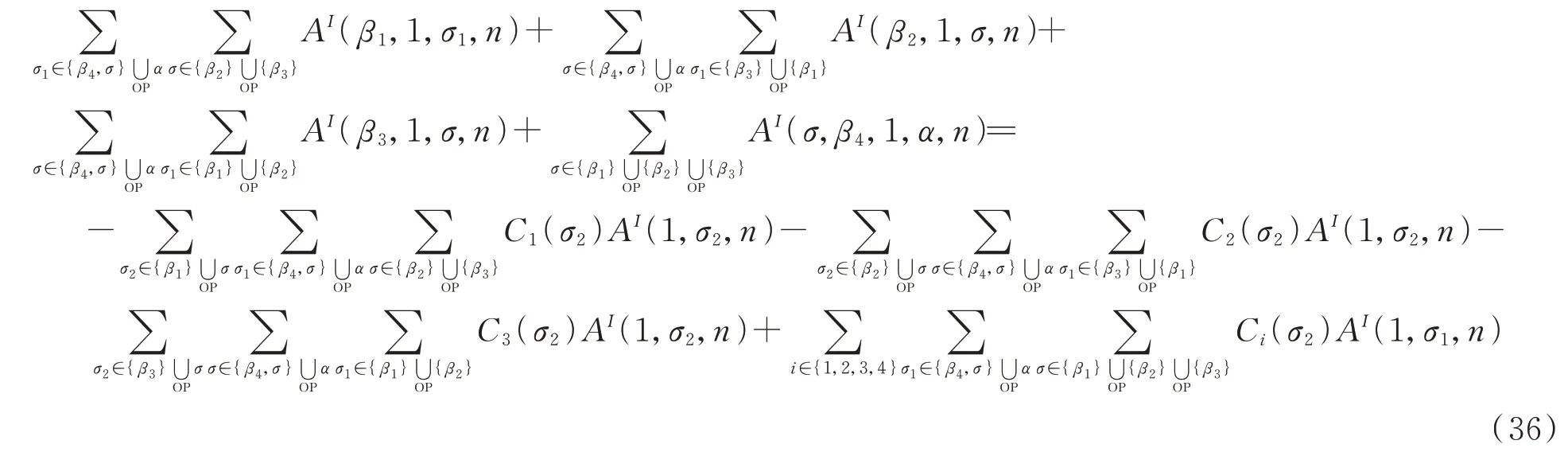
（35）和（36）式这两个关系就是弦散射振幅的图基BCJ和KK关系。在场论极限下，（36）式变为

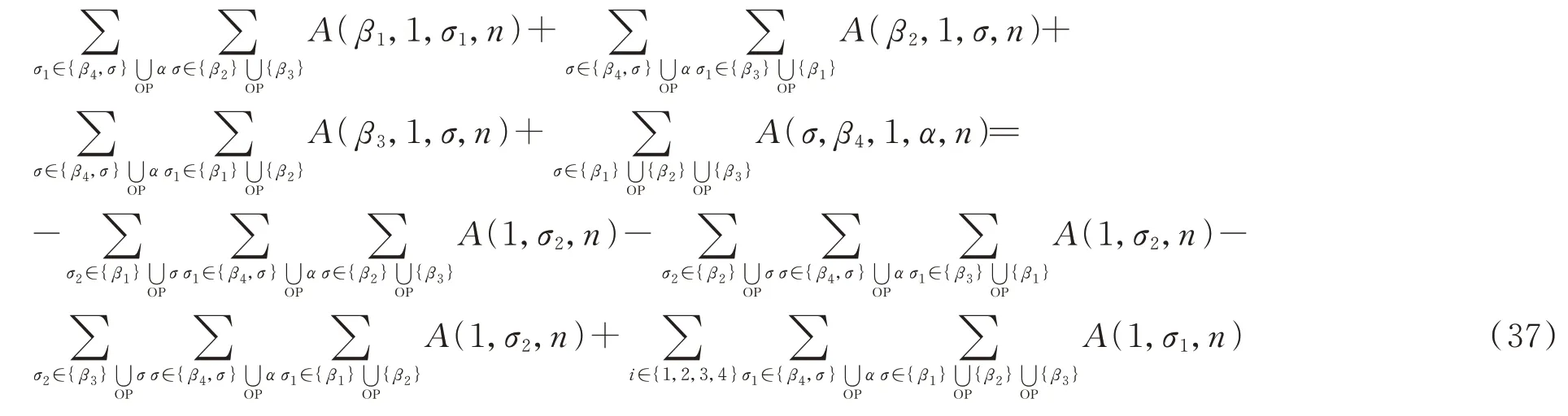
下面证明在场论极限下，（35）式退回到场的图BCJ关系。场论极限下（35）式可写为

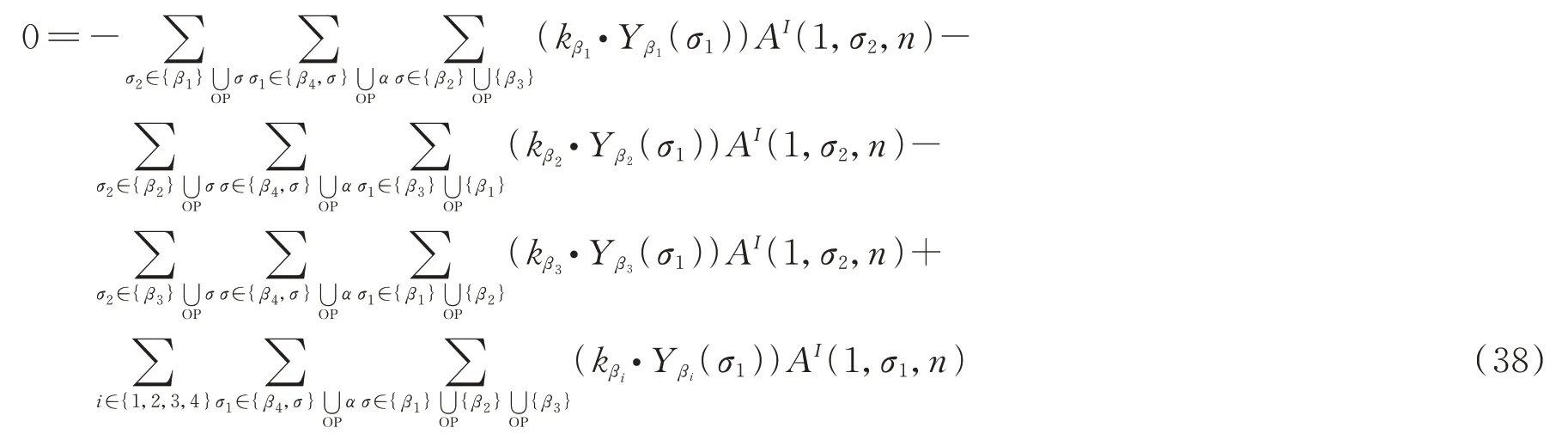
（38）式右边的第四项i=1部分可以写成

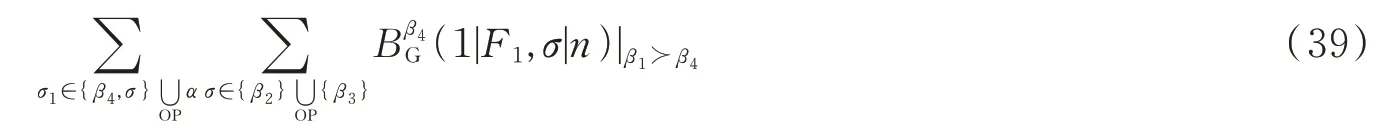
其中F1表示由β1组成的单点图。（39）式和（38）式右边第一项相加，得到如下结果

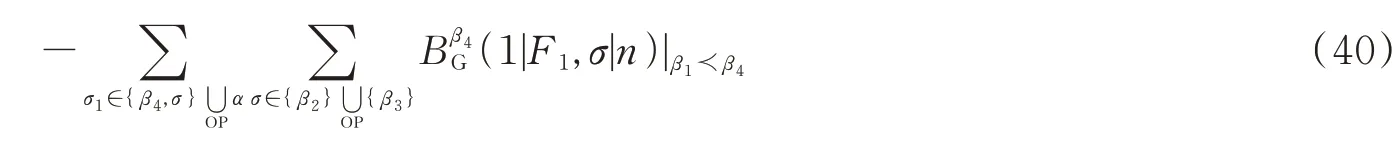
同样的方法处理（38）式右边的第四项i=2，3部分也能得到

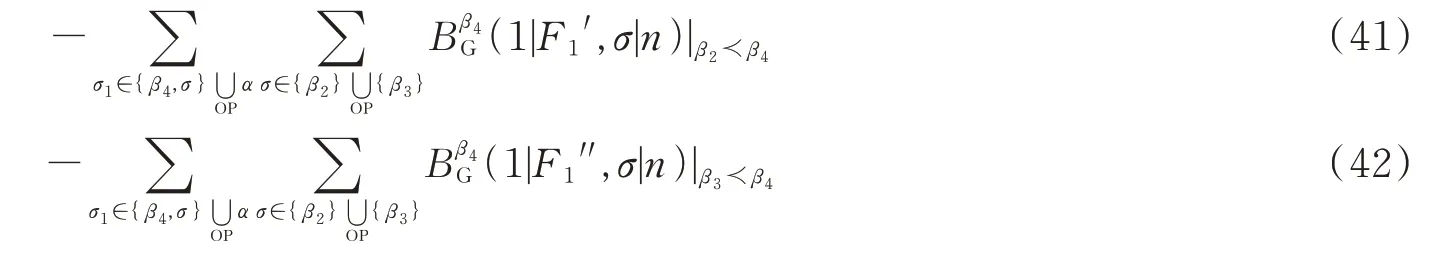
3 结语

从本文的证明中可以看出，弦论中的开弦散射振幅关系与杨-米尔斯场的散射振幅关系存在对应。通过找到弦论振幅的图基关系，并对其虚部取场论极限，就能方便地得到场论中的图基BCJ关系。若对其实部取场论极限，可得到与图基BCJ关系相伴随的新关系。这一证明方法更加清晰地揭示了场论振幅与弦理论振幅之间的关联。如何将相关讨论推广至圈级振幅，仍有待进一步研究。