基于差分进化算法的教育资源分配模型

刘宝宝,王贺应,陶 露,杨菁菁

(西安工程大学 计算机科学学院，陕西 西安 710048)

0 引 言

教育资源配置均衡不仅关乎着我国教育事业的发展，而且体现着教育事业的公平公正，在教育体系中发挥着重要作用。教育的可持续发展能够使其保持着生机和活力，促进创新型人才的培养。教育资源分配不均会导致教育质量的非均衡性发展，在一定程度上会对教育的可持续发展产生阻碍。教育资源分配不均衡还会影响基层教育目标的实现，影响着学生的德智体美劳全面发展。如何有效并合理地分配教育资源是教育管理部门的一项重要工作，也是一项严峻的挑战。文献[1]提出了由于教育资源分配不均产生的部分社会问题，如教育服务于市场并与房地产市场紧密联系，从而出现了“学区房”相关问题。教育资源分配不均还会加剧课外辅导热。因此，对教育资源进行合理的分配是促进区域教育均衡发展的重要环节。文献[2]认为教育资源的不均衡是资源分配不合理和固有的教育体制所引起的。优化教育资源在一定程度上促进了教育资源分配的均衡发展，同时可以有效地减少教育资源不均所带来的不利因素。

目前大部分教育资源的分配是依靠人工统计完成，存在成本高、效率低、统计工作复杂等问题。不利于教育事业的发展。近年来，智能算法在教育事业统计和资源分配方面的应用引起了研究者的关注。文献[3]以某13个区县原有的教育资源数据为依据，提出基于粒子群算法的教育资源分配模型，在一定程度上改善了教育资源的分配不均衡问题。粒子群[4](particle swarm optimization, PSO)算法是群体智能算法的一种[5]。该算法通过群体中个体之间的协作和信息共享寻找最优解,每个粒子视为一个个体[6]，并且具有速度特征和位置特征，分别表示粒子移动的快慢和方向，在迭代过程中粒子的速度和位置会不断更新变化[7]。PSO算法的优势在于简单、容易实现，并且只需要调整少许的参数。但该算法在数据维度较高时，容易陷入局部最优解[8]，需要较大的迭代次数才能使适应度值收敛。

本文提出了一类基于差分进化(differential evolution, DE)算法的教育资源分配模型，该模型结构简单、参数较少、性能优越。DE算法具有内在并行性，种群中的个体之间可以协同搜索。在相同的条件下，DE算法具有较快的收敛速度，能够实现教育资源合理有效的分配[9]。与基于PSO算法的教育资源分配模型相比，该模型在迭代速度、运行时间方面具有一定的优势。为了验证此模型对教育资源分配的有效性，文中还建立了基于人工鱼群算法[10](artificial fish swarms algorithm，AFSA)的教育资源分配模型，实现了某13个区县教育资源数据分配的图形用户界面(graphical user interface, GUI)，为教育管理部门提供资源分配依据，同时为教育统计大数据模型的优化提供一定的理论基础。

1 教育资源分配模型的建立

1.1 DE算法

DE算法是一种基于群体差异的启发式并行搜索方法[11]，群体中每个个体对应一个解向量。该算法的流程与遗传算法相似，都包括变异、交叉和选择操作，但这些操作的具体定义与遗传算法有所不同。

DE算法的基本思想是从某一随机种群开始，对个体进行初始化、变异、交叉和选择操作，最终保留最优个体[12]。该算法具有较强的搜索能力[13]，是一种高效的全局优化算法。首先，种群经过初始化操作,从中随机选择2个不同的个体进行差分和缩放[14],并从种群中再随机挑选个体进行向量合成进而产生变异个体；然后，对父代个体和变异个体进行交叉操作[15]，从而获得新的个体；最后，对个体与父代个体的适应度值进行比较,选择个体适应度值最优的个体进入下一代继续迭代，直到满足终止准则[16]。具体分5个步骤。

1) 初始化。在解空间里随机产生满足约束条件的N个由D维向量组成的个体[17]，第i个个体的j维取值方式为

(1)

(2)

(3)

4) 边界条件处理。DE算法经过交叉操作和变异操作后，可能会导致种群中部分个体范围超出给定的范围。假设u的范围是[v,w],u′是经过交叉和变异操作后产生的新个体，需要对上述操作后得到的个体进行边界条件判断并做出相应的处理。处理方法一般有2种：

ⅰ) 边界吸收，

(4)

ⅱ) 重新随机生成新的个体，即当u′w时,

u′=v+rand(0,1)×(w-v)

(5)

5) 选择。选择操作使用锦标赛选择机制，从种群中的个体和通过变异和交叉操作得到的个体中选择出最好的个体进入下一代[21]。具体方式为

(6)

算法通过不断的迭代计算，保留优良个体，淘汰劣势个体，引导搜索过程向全局最优解逼近，最终输出最优结果[22]。

1.2 教育资源分配模型的实施

基于DE算法的教育资源分配模型流程如图1所示。

图 1 基于DE算法的教育资源分配模型Fig.1 Educational resource allocation model based on DE algorithm

Step 1 初始化种群并进行归一化。根据目标函数计算初始化种群中的个体，得到每个个体的适应度值。该模型的种群规模NP影响着算法的寻优能力：NP越大，种群的多样性也就越好，寻优能力也就越强。但NP不能过大，否则会增加计算难度。综合考虑,此模型中的种群规模NP取20。

Step 3 验证结束条件。基于DE算法的教育资源分配模型分配教育资源的结束条件为当前的迭代次数超过初始化的迭代次数，或者为多次迭代后，适应度值的结果没有发生变化，教育资源分配模型流程结束。为了缩小区县之间教育资源分配不均衡的状况，假设现有1 000名新招教师和100 000册新图书要分配到这13个区县。基于DE算法的教育资源分配模型中算法的迭代次数根据分配教育资源数目的不同而不同：根据教师资源数，在教师分配时模型的迭代次数设置为200；在分配图书册资源时，模型的迭代次数为2 000。教育资源分配模型根据教育资源分配数目的不同，迭代次数取不同的值，进而保证基于DE算法的教育资源分配模型寻优结果的全局最优性[3]。

1.3 目标函数

本文模型采用了文献[3]中的均方差作为适应度值函数，适应度值的表示为

(7)

式中:Yi表示教育资源分配到各区县之后的适应度总值，i≥1；Y0表示初始适应度总值，且初始值为0;Ni表示分配前各区县的资源总数;ni表示教育资源分配模型分配到各区县的资源数;si表示各区县的学生人数。已知待分配的资源总数和原有的教育资源数，式(7)中仅存在一个变量，即待分配到各区县的资源数ni。Yi的值恒大于零，分配资源ni≥0。经过上述分析，若要降低Yi的值，需要将教育资源优先分配给低于总区县资源平均值的区县。

2 仿真实验

本文使用文献[3]的统计数据,见表1。表1中，生师比越小表示每位教师能够更有效地辅导学生； 生均图书册数值越大表示每个学生可拥有图书册的数量越多。通过表1中的统计数据可以看出，部分区县之间的生师比和生均图书册数存在着较大的差距，说明了原有的教育资源分配不均衡的情况比较严重。

为了改善区县之间原有的教育资源分配不均的现状，教育资源分配模型会根据目标函数，在分配资源的过程中适当地降低生师比，提高生均图书册数，使得区县之间的生师比和生均图书册数尽可能地趋于均衡状态。

表 1 教育资源统计数据[3]

2.1 生师比分配

根据目标函数，基于DE算法的教育资源分配模型会将教师优先分配给生师比较高的区县，从而降低适应度总值Yi。模型会比较各个分配方案的Yi值，并将Yi取最小值时所对应的分配结果作为最佳方案，从而降低区县之间教师资源的差距。

表2分别给出了基于DE算法和PSO算法的教育资源分配模型对1 000名教师进行分配的结果。从表2中可以看出:2种模型具有相近的教育资源分配性能，5个生师比较高的区县，即区县11，10，8，12和7都有新教师被分配，在一定幅度上降低了这5个区县的生师比的比值。

图2描述了基于DE算法的教育资源分配模型分配教师资源前后的生师比变化趋势。

图 2 各区县生师比分配前后对比

从图2可以看出：各区县生师比分配前，区县11的生师比接近12，而区县4的生师比仅有3.456，原有的教师资源分配差距较大；分配后，区县11、10、8、12和7的生师比都有着明显的下降趋势。从而验证了该模型在分配教师资源方面能够有效改善区县之间教师资源分配不均衡的问题。因此，应用该模型对教师资源进行分配，能够有效地缩小各个区县生师比的差距，在一定程度上改善教师资源分配不均衡的现况，促进教育事业的公平公正。

表 2 生师比变化情况

2.2 生均图书册分配

表3分别给出了基于差分进化算法的教育资源分配模型和基于POS算法的教育资源分配模型对100 000册图书进行分配的结果。

表 3 生均图书册数变化情况

从表3可以看出：2种模型都能对图书资源进行合理的分配，提高了部分区县的生均图书册数，并且具有相近的分配结果。

图3描述了基于DE算法的教育资源分配模型分配图书册资源前后的生均图书册数变化趋势。

图 3 各区县生均图书册数分配前后对比Fig.3 The number of books before and after allocation of each area

从图3可以看出，区县之间的生均图书册数的差异较大，最小值是最大值的1/4，图书册数资源分配不均衡的情况比较严重。经过对图书册数资源数据的分析，个别区县原有的图书册数多达190多万册，少则26万册，所以13个区县总的图书册数基数差异较大。而待分配的图书册数仅有10万册，相比原有的图书册总数差距较大。经过教育资源分配模型的分配，图书仅分配到图书资源较少的2个区县，即区县10和区县12，但生均图书册数在各区县之间的差距并没有得到根本的改善。

可见，通过教育资源分配模型对图书册数进行分配，并不能从根本上改善区县之间生均图书册数的差距。若想改善由于基数过大而造成的教育资源分配不均衡的问题，需要耗费大量的财力和人力才可能缩短区县之间的教育资源差距。所以，在初始的图书册数分配阶段，应充分考虑图书册数资源的分配是否合理，而不能只依靠教育资源分配模型分配新的图书解决区县之间的图书册数资源不均衡问题。

2.3 不同教育资源分配模型的比较

为了进一步说明基于DE算法的教育资源分配模型的有效性，建立了基于AFSA的教育资源分配的仿真模型。通过大量的仿真实验数据，验证了DE、PSO及AFSA等3种智能算法的教育资源分配模型的分配结果相近，但在算法的执行效率上有所差异。

从教育资源适应度值的收敛趋势、教育资源适应度值收敛时的平均迭代次数、教育资源分配模型的时间复杂度以及模型分配教育资源的平均运行时间(单位：s)等4个方面对3种智能算法的教育资源分配模型进行比较和分析。图4、5分别描述了3种智能算法教育资源分配模型教师资源分配和图书册资源分配所得到的适应度值收敛趋势。

图 4 教师资源适应度值收敛趋势Fig.4 Convergence trend of teacherresource fitness value

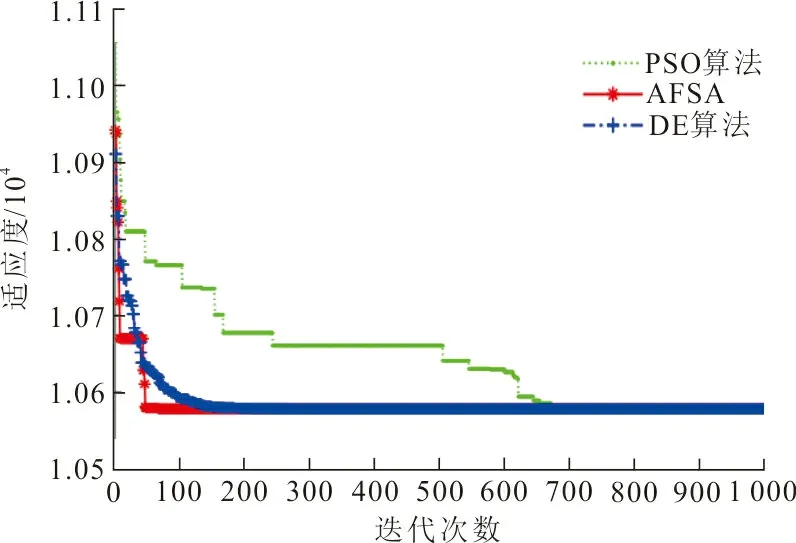
图 5 图书册数资源适应度值收敛趋势Fig.5 Convergence trend of book resource fitness value

表4为3种模型在分配教育资源过程中，适应度值收敛时平均迭代次数。

表 4 适应度值收敛时的平均迭代次数

从表4可以看出，基于PSO算法的教育资源分配模型的迭代次数最高，收敛速度最慢。其主要原因在于PSO算法在处理高维度问题时容易陷入局部最优解，所以算法需要较长的迭代的次数才能使适应度值收敛。基于AFSA的教育资源分配模型的迭代次数最低，收敛速度最快，是因为人工鱼群算法具有并行处理的能力[25]，即人工鱼群通过并行搜索进而寻找最优解。AFSA中的聚群行为能够使算法快速摆脱局部最优解，追尾行为能使算法在较少的迭代次数中使适应度值达到收敛，从而加快AFSA寻找最佳适应度值的速度。

分析3种资源分配模型的时间复杂度:设m为算法的迭代次数;n为种群的数目;D为维度，即区县的个数;t为人工鱼群算法中鱼群的尝试次数。计算得出基于AFSA的教育资源分配模型具有较高的时间复杂度,为O(m·n·D·(t+n));基于PSO算法的教育资源分配模型和基于DE的教育资源分配模型具有相同的时间复杂度,即O(m·n·D)。不过，基于DE的教育资源分配模型与基于PSO算法的教育资源分配模型相比，需要较少的迭代次数便可以获得最优解。

表5为3种模型在分配教育资源过程中，适应度值收敛时平均运行时间。

表 5 教育资源分配模型的平均运行时间

从表5可以看出，基于DE算法的教育资源分配模型的平均运行时间最短，而基于AFSA的教育资源分配模型的平均运行时间最长。因为AFSA包括觅食行为、聚群行为、追尾行为和随机行为等4种行为，在算法的每一次迭代中，计算过程比较复杂，因此该模型在分配教育资源的运行时间较长，分配效率较低。

经过对3种模型的综合分析可以得出：AFSA的教育资源分配模型在分配教师资源时能够在较少的迭代次数使适应度值达到收敛，但模型得到最终分配结果所运行的时间最长。随着教育资源数据量的增大，DE算法的教育资源分配模型和AFSA的教育资源分配模型都能够在较少的迭代次数中使适应度值收敛，而PSO算法的教育资源分配模型仍需较多的迭代次数才能使适应度值收敛。在3种资源分配模型中，AFSA教育资源分配模型的运行时间远大于DE算法教育资源分配模型的运行时间，资源分配的效率较低。通过比较和分析，验证了DE算法的教育资源分配模型的有效性。

3 MATLAB的GUI仿真

利用MATLAB GUI能够设计出人机交互式的图形化界面，方便用户使用。用户在GUI界面上执行相关操作便可以使计算机运行相关的回调函数，进而显示用户所期望的输出结果。因此，为了更加直观地显示3种模型分配教师和图书册数资源的差异，图6构建了3种模型对某13个区县的教育资源数据分配结果的可视化界面。其GUI界面主要包括资源分配的按钮、资源分配所需要的时间、资源分配结果的展示和教育资源分配模型适应度值的收敛趋势等4个模块。

图 6 教育资源数据分配可视化界面Fig.6 Educational resource data distribution visualization

用户在GUI界面的资源分配模块中，输入待分配的教育资源数后，点击分配教师资源模块中的PSO_TE按钮，则会在资源分配结果展示模块中的左侧表格中显示一列PSO教育资源分配模型分配教师资源的方案，同时也会在模型收敛趋势的模块中显示该模型分配教师资源时适应度值的收敛趋势。DE_TE按钮和AFSA_TE按钮的功能与PSO_TE按钮相同。点击分配图书册资源模块中的PSO_Book按钮，则会在资源分配结果展示模块中的右侧表格显示PSO教育资源分配模型分配图书册资源的方案，同时也会在模型收敛趋势的模块中显示该模型分配图书资源时的适应度值收敛趋势。DE _Book按钮和AFSA _Book按钮功能等同于PSO_Book按钮，会分别展示模型分配图书册资源的结果以及适应度值的收敛趋势。

点击Teachers按钮，则会在资源分配结果的模块中的左侧表格显示3种教育资源分配模型分配教师资源的方案，在教师资源分配时间模块也会分别显示3种模型分配教师所执行的时间，同时在模型收敛趋势的模块中显示3种模型分配教师资源的适应度值收敛趋势。Book按钮有3种教育资源模型对图书册资源进行分配的功能,并显示图书册资源分配的结果、模型运行的时间对比和模型分配图书资源时的适应度值收敛趋势。

4 结 语

教育资源的合理分配对于教育管理部门是一个挑战。资源分配到各个区县后，还需要分配到具体的学校或者教育机构，是一项比较繁琐的任务。在教育资源分配的过程中，需要考虑各区县原有的资源情况，尽可能地改善教育资源分配不均衡。从资源分配的结果分析，当待分配的资源与原有的教育资源的总基数相差不大时，使用教育资源分配模型分配教育资源，可以适当地缩小区县之间的差距，从而使得教育资源的分配更加科学合理。对于某些教育资源基数过大的问题，则需引起教育管理部门的重视。在今后的教育机构基础建设时，应充分考虑到教育区域资源的均衡问题，否则区县之间的教育资源差距不易缩小。

此外，本文的模型是基于差分进化算法提出的，即算法中的缩放因子F为固定值。F过大会降低模型的收敛速度；F过小会降低种群的多样性。同理，交叉算子CR也可以设置动态值，保持种群的多样性。因此，在未来的工作中，基于改进的DE教育资源分配模型可以将缩放因子F设置为动态的值：在算法的迭代初期F较大，可以保持种群的多样性，加快寻找最优解；随着迭代次数的增加，可以适当减小F值，以保存种群中的优良个体，避免破坏最优解，从而更加合理有效地分配教育资源，逐渐缩短各区县之间的差距。