云计算辅助的高效决策树隐私保护查询协议
秦宝东,李媛媛,余沛航
(西安邮电大学 网络空间安全学院,陕西 西安 710121)
机器学习[1]是一种使用历史数据训练出模型,然后通过对模型输入新的数据来进行预测的方法。在当今的大数据时代,机器学习技术取得了突破性的进展,在无人驾驶汽车、垃圾邮件过滤等领域应用广泛,在医疗诊断领域也有着良好的发展前景[2]。然而,机器学习本身面临着许多安全与隐私问题[3-4]。模型训练需要大量的训练数据,其预测的准确性与训练数据的多少以及数据质量相关。训练数据通常包含诸如个人工作、爱好、身份信息和家庭状况等涉及到个人隐私的信息,必须利用密码技术进行保护[5]。如果将这些信息以明文的形式传输,一旦被泄露,可能会造成严重后果。而且,大量训练数据的计算全部交给服务器完成,可能会超出服务器的计算能力,从而导致整个系统效率减慢甚至系统崩溃。
在早期的工作中,机器学习隐私保护主要重视模型训练阶段数据的隐私保护,如基于差分隐私[6]、(全)同态加密[7-8]和安全多方计算[9]等密码技术的安全机器学习模型。除了保护训练数据的隐私,近年来,越来越多的学者更加关注隐私保护的机器学习分类研究,特别是用户特征向量、分类模型和预测结果的隐私保护[10-11]。
2015年,Bost等[10]研究了超平面分割(Hyperplane Decision)、朴素贝叶斯(Naïve Bayes)和决策树(Decision Trees)等3种分类模型的隐私预测协议,主要使用半同态加密技术实现协议中的加、乘、比较等基本运算。但是,对于决策树模型,需要将决策树模型表示成一个高次多项式函数,并使用效率较低的全同态加密技术实现密文数据上的高次多项式运算。2016年1月,Gilad-Bachrach等[11]提出一种基于同态加密的深度学习隐私保护方案用于医疗系统中,对患者病历中的敏感信息进行保护。医院将患者的信息加密后发送给服务器,服务器对加密数据进行预测,并将预测结果返回给医院进行解密使用,该方案在MNIST(Mixed National Institute of Standards and Technology database)数据集上训练的准确率为98.95%,不但保证了准确性和安全性,同时也实现了较高的吞吐量。同年7月,Wu等[12]利用不经意传输协议和加法半同态加密技术替代全同态加密实现Bost等人的决策树隐私预测协议,从而提高了协议的效率。但是Wu等人的协议需要将决策树模型发送给用户,在发送给用户之前,服务器需要先对决策树模型进行随机化并且转化为完全二叉树,从而增加了用户与服务器之间的通信及计算开销。 2017年,Tai等[13]改进了Wu等人协议的效率,提出一种基于线性函数的决策树隐私保护查询协议,用线性函数取代高次多项式函数表示决策树模型,并利用路径权重是否为零判断二叉树叶子节点是否包含分类结果,从而降低决策树预测协议的总体运行时间。但是,当决策节点稀疏时,该协议需要用户与服务器交互两轮,用户端的计算效率并没有提高。
除了解决用户和模型提供者之间的隐私预测协议,还有一部分工作将用户特征向量和决策模型同时外包给两个云服务器来实现隐私预测协议[14-15]。该类协议一般通过秘密拆分和安全计算解决协议中的一些常规运算,而不需要同态加密方案,因此效率一般较高。但是,该类协议需要引入可信密钥中心预分配一些秘密信息到两个服务器,从而保护用户数据和预测模型的隐私性。针对基于线性函数的决策树隐私保护查询协议存在的不足之处,拟提出一种云计算辅助的高效决策树隐私保护查询协议,以期在一定程度上改善客户端的计算和通信开销。该协议包含用户、决策服务器和云计算辅助服务器等3个实体。以医疗系统为例,协议的用户是拥有一些疾病特征向量的患者,决策服务器是拥有一个决策树分类模型的医院。首先,用户利用云计算辅助服务器的公钥将自身的疾病特征向量加密后安全地传送给医院。其次,医院和云计算辅助服务器通过运行比较协议,计算出决策树中每条路径的权重和,将该权重和利用云计算辅助服务器的公钥进行加密,而相应的分类结果用云计算辅助服务器的公钥和用户的公钥进行双重加密,并将密文发送给云计算辅助服务器。再次,云计算辅助服务器通过判断每条路径的权重和是否为零,将正确的分类结果部分解密后返回给用户。最后,用户利用自己的私钥恢复出正确的分类结果。
1 基础知识
1.1 同态加密
同态加密是一种加密形式,用户对密文进行特定运算得到的结果仍然是密文,且和对明文进行相同运算后再加密得到的结果具有相同的分布,其分为全同态和半同态两种形式。半同态加密是指已知两个密文E(e,m1)和E(e,m2),用户可以计算出明文m1+m2的密文E(e,m1+m2)。下面给出同态加密的形式化定义。
定义1一个(加法)同态加密方案包含以下4个概率多项式时间算法并满足正确性和同态性。
1)系统参数生成算法S(1λ)。输入安全参数λ,输出系统参数s=S(1λ)。无特殊说明外,其他算法都将s作为其输入参数的一部分。
2)密钥生成算法G(s)。输入系统参数s,输出公钥e和私钥d,其中公钥定义了消息空间M和密文空间C。
3)加密算法E(e,m)。输入公钥e和消息空间上的一个消息m,输出密文c=E(e,m)。无特殊说明外,[m]e表示消息m在公钥e下的密文。当公钥明确时,可省略其下标,简记为[m]。
4)解密算法D(d,c)。输入私钥d和密文c,输出明文m=D(d,c)。
正确性对于任意系统参数s,密钥(e,d)←G(s)和消息m∈M,则有
D[d,E(e,m)]=m
同态性对于任意消息m1,m2∈M及其密文c1和c2,存在一个多项式时间算法H,则H(c1,c2)输出一个密文c并满足D(d,c)=m1+m2。
LEE[16](Lifted ElGamal Encryption)同态加密方案在DDH(Decisional Diffie-Hellman)假设下满足不可区分选择明文攻击安全性,即语义安全性,具体构造如下。
1)系统参数生成算法S(1λ)。λ选取一个循环群(,p,g),其中p和g分别是群的阶和生成元,输s=(,p,g)。
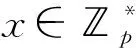
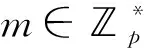
(c1,c2)=(gr,hrgm)

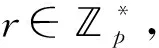
H([m1],[m2])=(grc1,1c1,2,hrc2,1c2,2)
显然,H([m1],[m2])≡[m1+m2]。
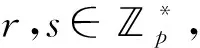

下面介绍双重LEE加密方案满足的3个性质。
性质1交换加密顺序,其密文是等价的,即两个密文的解密结果一样,表示为
[[m]e1]e2=[[m]e2]e1
根据性质1,将消息m的双重LEE加密简记为[[m]]。
性质2双重LEE加密方案满足同态性,即已知消息m1和m2的双重加密密文,存在算法H1计算消息m1+m2的双重加密密文,即
H1([[m1]],[[m2]])≡[[m1+m2]]
性质3已知消息m1在公钥e1下的LEE密文[m1]e1、消息m2和公钥e2,存在算法H2计算消息m1+m2的双重LEE加密密文,即
H2([m1]e1,m2)≡[[m1+m2]]
类似地,已知公钥e1和e2下的两个密文[m1]e1和[m2]e2,则存在算法H3计算消息m1+m2的双重LEE加密密文,即
H3([m1]e1,[m2]e2)≡[[m1+m2]]
1.2 比较协议
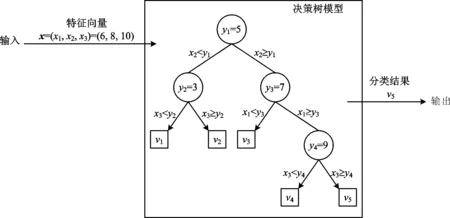
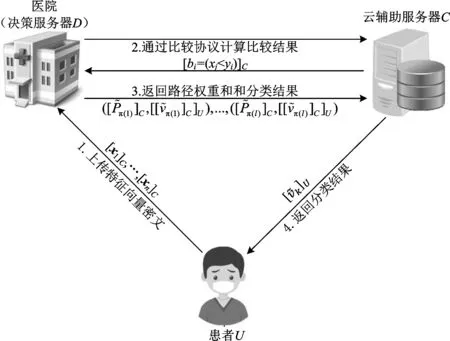
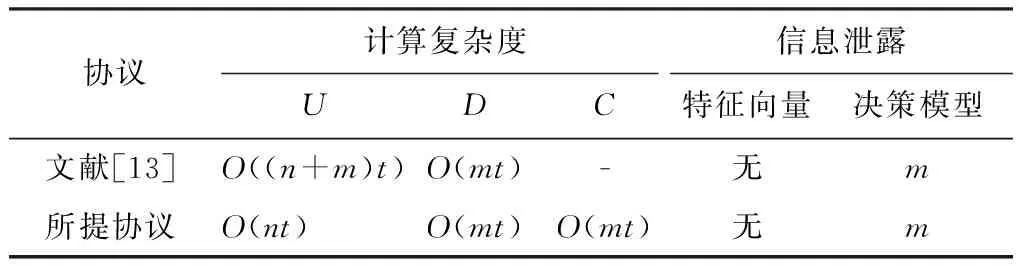
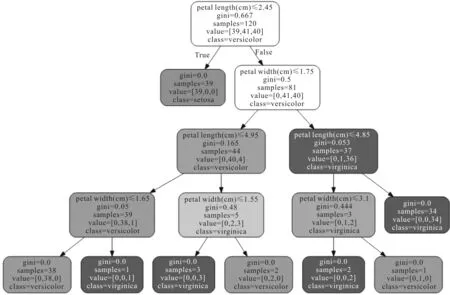
2008年,Damgård、Geisler和Krøigaard提出一种安全比较协议[17](简称DGK安全比较协议)。该协议假设用户A和用户B分别持有t比特的正整数x和y,并且A拥有一对同态加密算法的公私钥(e,d),通过运行DGK安全比较协议,B将获得加密后的比较结果,即[b]=[(x 图1 DGK安全比较协议运行过程 [x]表示对x按比特加密的结果,即 [x]=([xt-1],…,[x1],[x0]) PvtCmpA(d,c)算法的具体步骤如下。 输入私钥d和密文向量c=(ct-1,…,c1,c0)。 输出bA。 步骤1对于任意0≤i≤t-1,利用私钥d计算密文ci的解密结果mi←D(d,ci)。 步骤2如果存在解密结果满足mi=0,则返回bA=1。 步骤3如果所有解密结果都不满足mi=0,则返回bA=1。 PvtCmpB([x],y)算法的具体步骤如下。 输出c和bB。 步骤1选择一个随机比特bB∈{0,1}。 步骤2令s=1-2bB。 步骤4输出密文向量c=(ct-1,…,c1,c0)和随机比特bB。 决策树是一种常见的机器学习模型。一个决策树模型包含若干中间节点(决策节点)和叶节点(分类结果)。每个决策节点具有一个决策陷门值yi,每个叶节点具有一个分类值vj。因此,一个决策树可以用所有决策节点的限门值构成的决策向量y=(y1,y2,…,ym)和相应的分类结果向量v=(v1,v2,…,vl)表示,其中m和l分别为决策节点和叶节点的数量。当决策树是一个满二叉树时,决策节点和叶子节点的数量满足关系l=m+1。决策树模型的输入是一组特征值向量,记作x=(x1,x2,…,xn),其中n是特征值的数量,输出是某一分类结果vi。决策树模型示例如图2所示,该模型示例包含m=4个决策节点和l=m+1=5分类结果。 图2 决策树模型示例 图2中,特征向量包含3个特征值,即输入特征向量x=(6,8,10),根据模型,输出分类结果v5。在明文状态下,通过比较特征值和决策节点值,很容易判断出分类结果。但是,这样会泄露输入的特征向量信息。通过DGK安全比较协议,决策模型持有者仅能获取比较结果,如b=(x 云计算辅助的高效决策树隐私保护查询协议包含决策服务器D、用户U和云辅助服务器C等3个实体。以医疗系统为例,决策服务器(医院)拥有一套训练好的疾病预测模型,用户(患者)具有某种疾病的特征值并期望利用预测模做出疾病诊断,其具体工作模式如图3所示。 图3 协议工作模式 假设每个特征向量包含n个特征值,决策树是一个满二叉树,即包含m个决策节点和l=m+1个叶子节点。令(x1,x2,…,xn)∈n和(y1,y2,…,ym)∈m分别表示特征向量和所有决策节点的限门值。每个特征值和决策限门值不超过t比特。用户和云辅助服务器分别拥一对LEE同态加密方案的公钥和私钥,记作(eU,dU)和(eC,dC)。该协议的详细执行步骤如下。 步骤1用户利用云辅助服务器的公钥将特征向量的每个元素按比特加密,并通过安全信道将加密结果[x1]C,[x2]C,…,[xn]C传送给决策服务器。 步骤2对于每个决策节点元素yi,令xj表示相应的特征值,其中1≤i≤m,1≤j≤n。决策服务器执行算法(ci,bi,0)←PvtCmpB([xj],yi)并将密文c1,c2,…,cm发送给云辅助服务器。 步骤3对于每个密文ci,云辅助服务器首先利用算法PvtCmpA(dC,ci)计算共享比特bi,1,然后利用自己的公钥加密每个共享比特bi,1,最后将密文[b1,1]C,[b2,1]C,…,[bm,1]C发送给决策服务器。 步骤4当收到密文[b1,1]C,[b2,1]C,…,[bm,1]C后,决策服务器进行以下计算。 (a)对于任意决策节点1≤i≤m,利用bi,0和密文[bi,1]C计算比较结果bi=bi,0⊕bi,1的密文,即[bi]C←[bi,0⊕bi,1]C。令决策节点i的左分支和右分支权重分别为wi,L=[1-bi]C和wi,R=[bi]C。 (b)对于任意叶节点Lk(1≤k≤l),计算从根节点到该叶节点路径权重之和Pk。 最后,决策服务器按上述排序结果发送给云辅助服务器。 假设用户、决策服务器和云辅助服务器都是诚实可信但好奇的,通过协议,3个实体能够获取以下信息。 1)用户可以提交任意(加密后的)特征向量给决策服务器,并从云辅助服务器获取正确的决策结果。 2)决策服务器可以获取任意特征向量的密文以及比较结果的密文。 3)云辅助服务器可以获取算法PvtCmpB输出的密文以及所有从根节点到叶节点路径权重和的密文和对应分类结果的密文。 此外,任意实体可以监听其他实体之间通信的内容,即模拟外部攻击者和单一实体共谋情况。协议的隐私性意味着用户仅能获取决策结果,而决策服务器和云辅助服务器不能够获取用户特征向量和分类结果的任何信息,除了特征向量的维数和长度。同时,云辅助服务器不能获取决策服务器的分类模型信息。 定理1若LEE同态加密方案是语义安全的,DGK安全比较协议是隐私保护的,并且决策服务器与云辅助服务器之间不共谋,则上述决策树查询协议是隐私保护的。 证明在协议的步骤1中,用户的特征向量用云辅助服务器的公钥加密后通过安全信道将加密结果传递给决策服务器。尽管云辅助服务器拥有解密私钥,但是利用安全信道的语义安全性,云辅助服务器等外部用户无法获取用户和决策服务器之间通信的真实信息,即特征向量的密文[x1]C,[x2]C,…,[xn]C,保证用户特征向量的语义安全性。决策服务器尽管可以获取特征向量的密文,但是没有云辅助服务器的解密密钥。根据LEE方案的语义安全性,决策服务器无法从特征向量的密文中获取任何有用信息。因此,用户与决策服务器之间的通信内容不会泄露用户特征向量的信息。协议中步骤2、步骤3和步骤4(a),相当于在云辅助服务器和决策服务器之间执行了一次DGK安全比较协议,根据DGK比较协议的安全性,决策服务器仅能获取比较结果的密文,即[bi]C根据加密方案的语义安全性,决策服务器从该密文中获取不到bi的任何有用信息。云辅助服务器仅能获取比较结果的随机拆分结果,即共享比特bi,1。 总之,通过上述决策查询协议,用户可以正确地获取分类结果,而不会获取其他决策模型的其他信息。决策服务器除了获取用户特征向量的长度,也不会获取特征值的其他信息。云辅助服务器除了能够获取决策模型的叶子节点数量,也不会获取决策模型以及用户特征向量的其他任何信息。 为了分析所提决策树隐私查询协议的性能,将其与基于线性函数的决策树隐私保护查询协议[13]进行对比。令n和t分别表示特征向量的维数和每个特征值的比特长度,m表示决策树中的决策节点个数。将一个实体到另一个实体的单向通信记作半次交互,双向通信记作1次交互。假设同态加密方案定义在循环群(,p,g)上,用群元素的数量表示通信量。用户、决策服务器和云辅助服务器端的理论计算复杂度及用户特征向量和决策模型泄露的信息对比如表1所示,各实体间协议交互次数和通信量对比如表2所示。 表1 两种协议计算复杂度对比 表2 两种协议通信量对比 通过表1和表2可知,所提协议利用云辅助服务器可以将文献[13]协议中用户端的O(mt)计算量转移至云辅助服务器,从而将用户端的计算复杂度从O((n+m)t)降至O(nt)。此外,用户与决策服务器的交互次数也由2次降至0.5次,同时增加0.5次用户与云辅助服务器的交互。因此,在所提协议中,用户参与的协议交互次数仅为1次,比文献[13]协议减少了50%。在信息泄露方面,两种协议都不会泄露用户特征向量的任何信息,而仅会泄露决策模型中决策节点的数量信息,即m。在通信量方面,用户参与的通信量之和为(2nt+2)个群元素,比文献[13]协议减少了(2mt+6m+2)个群元素。总而言之,借助云辅助服务器,所提协议不仅能够降低用户端的计算和通信复杂度,而且可以减少用户参与协议的交互次数。 下面利用鸢尾花和乳腺癌两种数据集训练的决策树模型检测上述两种协议的实际效率。鸢尾花品种预测模型和乳腺癌预测模型分别如图4和图5所示。在鸢尾花品种预测模型中,特征向量维数为n=10,决策树深度为d=5,决策节点数量为m=7,分类结果有“setosa”“versicolor”和“virginnica”等3种。在乳腺癌预测模型中,特征向量维数为n=15,决策树深度为d=9,决策节点数量为m=20,分类结果有“benign”和“malignant”两种。实验环境为一台电脑配备Inter(R) Core(TM) i5-4210M (2.6 GHz)处理器,4G运行内存和64位Windows 10操作系统。令p=2q+1是一个1 024比特的素数,其中q是一个强素数。实验选取的El-Gamal加密方案定义在模p生成的q阶循环子群上。两种协议的实验结果如表3所示。 图4 鸢尾花分类模型 图5 乳腺癌分类模型 表3 两种协议的实验结果 由表3可以看出,对于不同的数据集,由于训练出来的模型参数不同,使得两种协议的具体时间和通信开销并不相同,这与表1和表2中的理论分析结果是一致的。对于鸢尾花数据集,由于决策节点数量和特征向量维数较小,所提协议的用户计算时间与文献[13]协议区别并不明显。但是,当决策节点数量和特征向量维数较高时,如乳腺癌数据集,文献[13]协议的用户计算时间为11.27 s,而所提仅需要将近一半的时间,即6.61 s。在通信量方面,对于鸢尾花数据集,所提协议用户与两个服务器的通信量之和为0.16 MB,而文献[13]协议需要0.22 MB。对于乳腺癌数据集,所提协议用户的通信量比文献[13]协议的用户通信量减少0.23 MB,约为53%。 借助云计算技术,提出一种高效的决策树隐私保护查询协议。该协议通过同态加密技术保护用户特征向量信息不会泄露给决策服务器和云辅助服务器,同时保护决策树信息不会泄露给用户和云辅助服务器。性能分析结果表明,通过云辅助服务器,该协议用户的计算时间和通信量较以往相关工作都有一定程度的改进。但是,决策服务器和云辅助服务器之间的效率仍然较低。下一步,将考虑如何在保证协议安全的前提下提高服务器的效率以及如何将决策树模型安全、高效地外包给云辅助服务器。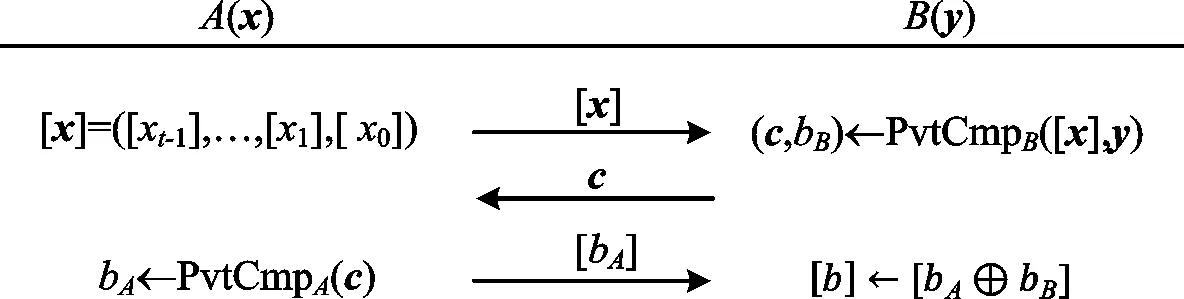

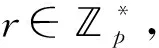
1.3 决策树模型
2 协议设计
2.1 协议描述
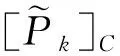
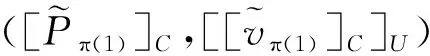
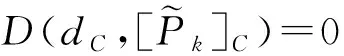
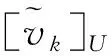
2.2 正确性分析
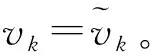
2.3 安全性分析
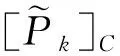
3 性能分析


4 结语

