一种改进的复合混沌系统及其性能

张雪锋，刘伟东，姜 文

(1.西安邮电大学 网络空间安全学院，陕西 西安 710121；2.国家计算机网络应急技术处理协调中心，北京 100029)

随着网络信息技术的迅速发展，大量的信息在网络上传播[1]，带来了隐私和机密泄露等数据安全问题。为此，提出了众多信息加密算法。其中，混沌在信息加密中有着重要的应用。

混沌是指在非线性动态系统中，不添加任何随机因素，由系统内部相互作用而产生的一种类随机现象[2]。混沌系统具有初值敏感性[3]、伪随机性[4]和遍历性[5]等性能，使得当混沌系统应用于加密算法时具有较好的雪崩效果[6]、安全性[7]和更大的密钥空间[8]。这些特点导致混沌系统成为加密算法的重要工具之一。

数字混沌系统可以分为一维混沌系统和高维混沌系统两类[9]。高维混沌系统具有更复杂的混沌特性，更大的混沌区间和密钥空间，更高维度的遍历性等特点[10]，但是，计算复杂度和实现成本比较高，限制了其实际应用[11]。相比之下，一维混沌系统的结构更加简单、计算成本较低，更加易于硬件实现。一些经典的一维混沌系统如Logistic、Sine、Cubic、分段线性混沌映射(Piecewise Linear Chaotic Mapping,PWLCM)和Tent等已经应用于相关的加密方案设计中[12-13]。但是，传统的一维混沌系统的初值敏感性和序列随机性较差[14]，混沌区间和密钥空间较小[15]，导致其应用在加密算法中的安全性较低[15]。

针对经典一维混沌系统安全性能较差的问题，有研究提出，在将一维混沌系统应用到加密方案的设计之前，先对一维混沌系统实施改进，改善其混沌特性，进而将其应用于加密算法中，以提升加密算法的安全性等性能[16]。例如，文献[11]提出了一种级联混沌系统(Cascade Chaotic System,CCS)框架，将任意两个一维混沌映射复合起来，第一个混沌映射的输出作为第二个的输入，第二个的输出又反馈到第一个作为输入进行循环迭代，从而将任意两个映射级联成为一个新的映射，然而，这种方法只有当两个混沌映射均具有较大的Lyapunov正值时，级联后的映射才会表现出更复杂的混沌特性。另外，如果多个混沌映射进行级联操作，会增高计算成本，导致硬件难以实现等问题。文献[17]提出了一种轮开关转化系统，通过控制密钥选取混沌映射，这种改进能够有效提高加密算法的安全性，但是，设计合适且高效的轮式开关转化系统较为复杂。文献[18]提出了一种组合混沌系统，将Logistic、Sine、Tent等3种一维映射进行组合，并通过控制参数取值范围，然后进行加法和取模操作，进而构造出新的一维混沌系统，这种构造方式改善了混沌区间小、混沌区间不连续等问题，但是，系统的Lyapunov值较低。文献[19]提出了一种级联组合的方式来改造底层的一维映射，将Logistic、Sine、Tent等3种一维映射的任意一种作为一级的输入，然后在3种映射中任选两种映射进行级联后再组合，取模得到混沌映射，该方案改善了混沌序列随机性差、混沌区间小等问题，但是系统的初值敏感性较低。文献[20]提出一种复合混沌系统(Integrated Chaotic System,ICS-I)结构模型对Logistic、Sine和Tent映射进行级联组合，得到的新映射比仅通过级联操作得到映射的Lyapunov值大，但是，存在混沌区间不连续，初值敏感性低的问题[21]。文献[21]提出了一种复合混沌系统，用一个子映射的输入去扰动主映射的输出，然后再和子映射相加取模得到新的映射，利用乘法器使得状态变量在相空间中的分布更好，但是，该方法混沌区间小，当混沌系统参数取值较小时，初值敏感性较差，另外，还存在系统框架对于映射的选取不够灵活等问题。

针对文献[20]存在的混沌区间不连续、初值敏感性低以及文献[21]存在的混沌区间小等问题，拟在文献[20]和文献[21]的基础上提出一种改进的复合混沌系统，应用Logistic映射和Sine映射作为种子映射，通过扩展系统参数对种子映射进行随机地复合和组合，取模得到混沌映射，以扩大混沌区间，提升初值敏感性，扩展系统参数个数，改善混沌区间不连续问题，生成随机性较好的混沌序列。

1 预备知识

主要介绍Logistic映射和Sine映射两种传统的一维混沌映射，以及文献[20]和文献[21]提出的两种构造一维复合混沌系统的方法。

1.1 Logistic映射

Logistic映射是一种经典的一维混沌映射[10]，其结构简单，在多种图像加密中得以应用。Logistic映射的定义[10]为

xn+1=μxn(1-xn)

(1)

式中：初始值x0∈(0,1)；控制参数μ∈[0,4],当3.569 9…<μ≤时，系统处于混沌状态。

1.2 Sine映射

Sine映射同样作为一种经典的一维混沌映射[10]，其定义[10]为

(2)

式中：初始值x0∈(0,1)；混沌系统控制参数μ∈[0,4]，当μ在区间(3.48,3.72)和(3.8,4)之内时，系统处于混沌状态。

1.3 一维复合混沌系统

文献[20]和文献[21]分别以Logistic、Sine和Tent等3种一维映射构建一维复合混沌系统。

文献[20]提出的ICS-I系统可以表示为

xn+1=(F(G(xn))+H(xn))(mod 1)

(3)

式中，F(xn)、G(xn)和H(xn)分别为Logistic、Sine、Tent映射中的任意一种。

文献[21]提出的一维复合混沌系统可以表示为

xn+1=((fmain·(fseed(xn))+fseed(xn))·r)(mod 1)

(4)

式中：系统参数r∈[0,4]；主映射fmain(xn)和子映射fseed(xn)分别为经典一维混沌映射Logistic、Sine和Tent映射中的任意一种。

Logistic映射和Sine映射虽然结构简单，但混沌区间小，容易被穷举攻击，安全性低。文献[20]的一维复合混沌系统的混沌区间不连续，文献[21]的一维复合混沌系统的混沌区间较小。

2 复合混沌系统

为了改善Logistic映射和Sine映射的动力学特性，受到文献[20]和文献[21]一维复合混沌系统的启发，拟提出一种一维复合混沌系统构建方法。该方法的主要思想是利用一个混沌映射的输入，扰动另外一个混沌映射的输出，看似只用到了两个混沌映射，实际上该混沌映射的最终输出序列受到3个混沌映射的动力学特性的影响。

提出的一维复合混沌系统可以表示为

xn+1=((μa·F(G(xn))+
(ca-μa)·F(xn))·μb)(mod 1)

(5)

式中：+和·分别表示浮点加法和乘法；(mod 1)运算是保证生成的序列位于(0,1)之间；混沌系统参数a∈[8,10],b∈[0,2],c∈(4,6],μ∈[0,4]；F(xn)和G(xn)分别表示Logistic和Sine映射的任意一种。

该方法将级联算子随机作用于F(xn)和G(xn)，在此基础上，对于F(G(xn))和F(xn)采用了加法和模的组合算子。F(xn)和G(xn)组合条件为，两个混沌系统的控制参数取值范围相同并且相空间也相同。

为了增强系统结构的灵活性，在构造映射的过程中，并不严格的区分主映射和子映射。改变F(xn)和G(xn)的顺序，对F(xn)和G(xn)进行随机选取复合和组合就能够生成不同的混沌映射，这种复合方式构造新映射的选择机会更多。

选取Sine和Logistic这两种映射作为种子映射，通过复合和组合相结合来构造如下4种一维复合混沌映射。

1)S(L)+L映射，其表达式为

(6)

式中：n为迭代次数；混沌系统参数a∈[8,10],b∈[0,2],c∈(4,6],μ∈[0,4]。

2)S(L)+S映射，其表达式为

(7)

3)L(S)+L映射，其表达式为

(8)

4)L(S)+S映射，其表达式为

(9)

3 仿真结果及分析

为了验证所提复合混沌系统的性能，使用Matlab 2019进行仿真。采用Lyapunov指数、分岔图、序列随机性、相关系数、平衡度、初值敏感性和位变化率等常用的测试指标[22-23]仿真复合混沌映射的性能，并与文献[20]和文献[21]提出的映射性能进行对比。选择的测试指标中：Lyapunov指数和分岔图反映了映射是否具有混沌行为以及混沌区间；序列随机性、相关系数和平衡度反映了产生混沌序列的随机性能；初值敏感性和位变化率反映了映射的初值敏感性。

3.1 系统参数的混沌范围

分岔图可以直观反映混沌映射的混沌区间，其是检验一个系统是否具有混沌行为的重要指标。分岔图中阴影区域对应混沌区域，利用混沌系统的分岔图可以直观地反映系统的混沌区间[22]。提出的4种复合混构造的4种映射性能相近，以S(L)+L映射为例，通过分岔图对除μ外的系统参数a,b,c的混沌范围进行仿真。S(L)+L映射不同参数的分岔图如图1所示。图中的阴影部分对应区域为混沌区域。从图1可以看出，在3个系统参数取值范围内，S(L)+L映射进入了混沌状态，表明在此范围内构造映射具有随机性。

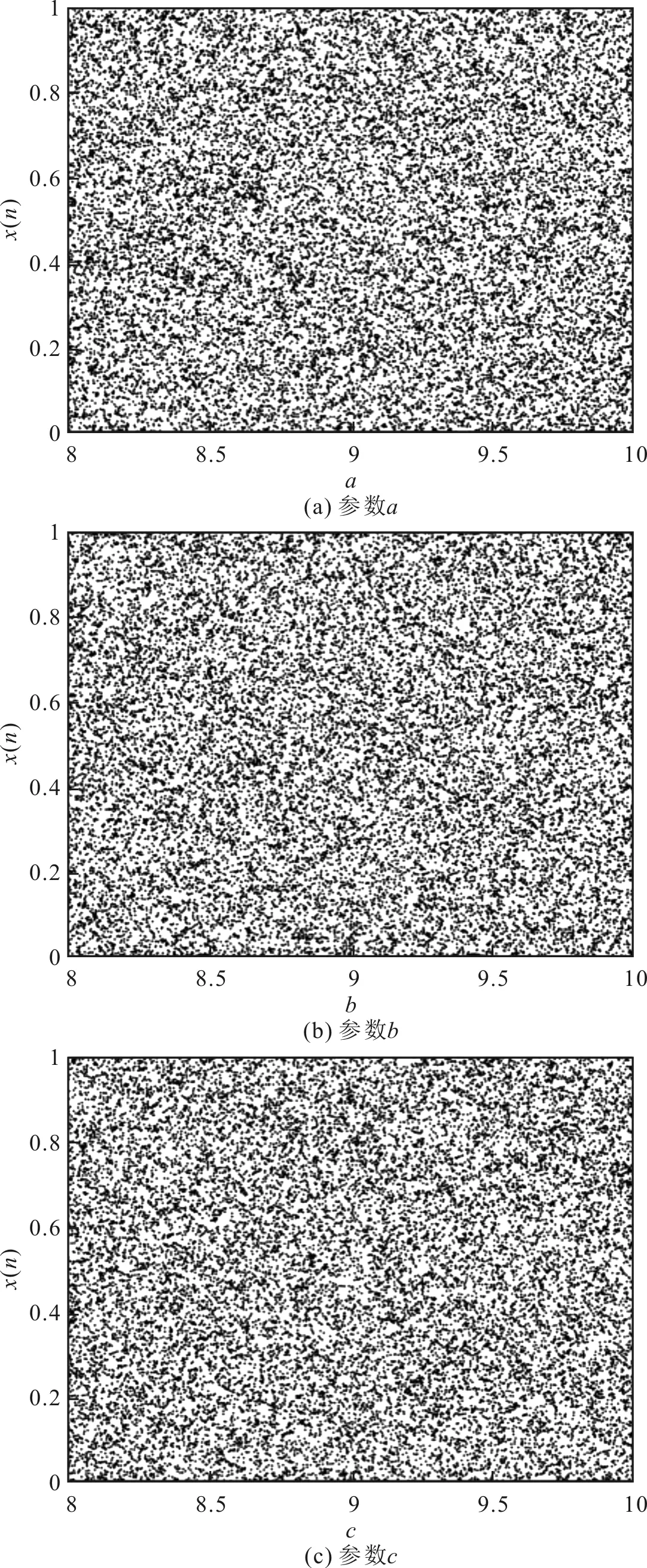
图1 S(L)+L映射不同参数的分岔图

3.2 Lyapunov指数

Lyapunov指数值能够有效地反映当变量值发生变化时，系统对于初始值的敏感性。李雅普诺夫指数(Lyapunov Exponent,LE)值大于0时的序列被称为混沌序列[22]。

构造4种映射的Lyapunov指数仿真结果如图2所示。从图中可以看出，当μ∈[0.1,4]时，4种映射的LE值始终大于0，并且没有奇异点的出现，说明当μ∈[0.1,4]时，提出的4种混沌映射均处于稳定的混沌状态。

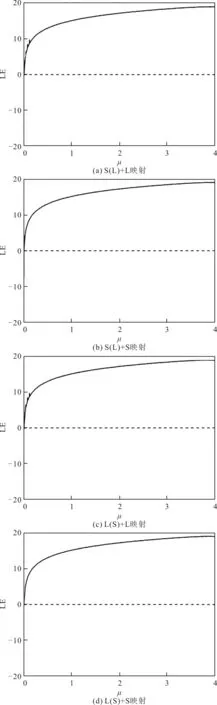
图2 4种映射的Lyapunov指数仿真结果

3.3 分岔图

参数在μ∈[0.1,4]的范围内，提出的4种复合混沌映射的分岔图如图3所示。可以看出，当μ∈[0.1,4]时，4种映射开始出现混沌现象，并且处于稳定的混沌状态，表现出复杂的混沌行为。

图3 4种映射的分岔图

文献[20]利用ICS-I复合结构生成的一维复合混沌映射有12种，这些映射的混沌区间均不连续。为了方便展示，选取其中的LT-L映射和LS-S映射作为例子进行展示。文献[20]中的LT-L映射和LS-S映射的分岔图如图4所示。从图中可以看出，文献[20]中的LT-L和LS-S两种映射的混沌区间均不连续，说明该映射的混沌状态不够稳定。当该两种映射被应用于图像加密过程中时，容易受到密钥穷举的攻击。

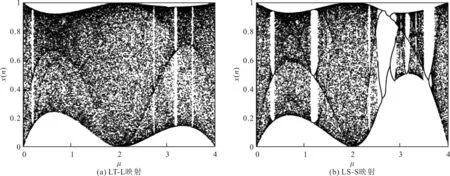
图4 文献[20]中两种映射的分岔图

文献[21]提出的复合混沌映射有两种，分别是TLT和TST映射。文献[21]中两种映射的分岔图如图5所示。从图中可以看出，当μ∈[1.05,4]时，文献[21]提出的TLT映射和TST映射出现混沌现象，处于稳定的混沌状态，表现出复杂的混沌行为。

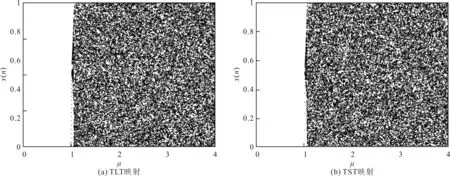
图5 文献[21]中两种映射的分岔图

对比图3、图4和图5可以发现，所提的复合混沌映射混沌区间为μ∈[0.1,4]，改善了文献[20]混沌区间不连续的问题以及文献[21]混沌区间小的问题，使用所提的混沌映射设计加密方案时，映射能够更快地进入稳定的混沌状态，另外，混沌区间的增大可以有效地抵抗密钥穷举攻击，算法的安全性也就相应提高。

3.4 随机性

混沌的随机性衡量其不可预测性，随机性越强混沌系统的保密性能越好。所提4种映射性能接近，文献[20]和文献[21]提出复合混沌映射的性能也各自比较相近。因此，为了方便结果展示，接下来，以所提出的S(L)+L映射为例，与文献[20]提出的LS-S映射和文献[21]提出的TLT映射进行随机性的仿真比较。

3.4.1 频数检验

将混沌序列经二值化处理得到二值序列。频数检验可以确保该序列里出现0和1的次数接近一致，其计算公式[23]为

(10)

式中：n1表示序列中1出现的次数；n0表示序列中0出现的次数；n表示生成的序列长度。

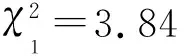
序列长度是10 000，对S(L)+L映射、TLT映射以及LS-S映射生成的序列进行频数检验，仿真结果如表1所示。

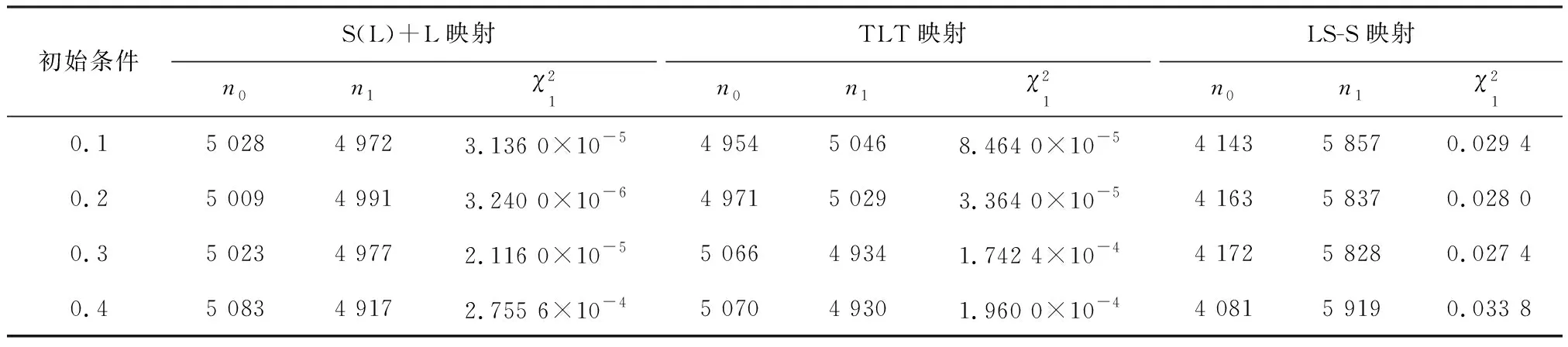
表1 3种混沌二值序列频数检验结果

3.4.2 随机性分布

设置混沌映射的初始值x0=0.40，序列长度取3 000，在系统参数μ的不同取值的条件下，文献[20]的LS-S、文献[21]的TLT和所提S(L)+L映射生成序列的随机分布图如图6所示。

从图6可以看出，当系统参数μ分别取4、3.7和1.05时，提出的S(L)+L映射生成序列均在整个(0,1)区间内有着近似均匀的随机性分布，而文献[20]提出的LS-S映射和文献[21]提出的TLT映射在μ取值不同的情况下，其生成序列有时候会位于(0,1)之间的中间区域，说明提出的S(L)+L映射在参数μ取值不同的情况下有着更好的随机性。

图6 3种映射生成的序列随机分布图

3.5 相关性

自相关系数和互相关系数是两个评价序列随机性的常用的统计指标。当其他参数改变时，序列自相关系数的变化越小，说明序列的随机性能越好；序列的互相关系数均越接近于0，说明序列的随机性能越好[23]。接下来，利用自相关系数和互相关系数指标来对比文献[20]的LS-S映射、文献[21]TLT映射和所提S(L)+L映射生成序列的随机性能。

3.5.1 自相关性

设定3映射的初始值x0=0.40，生成序列长度均为10 000。文献[20]的LS-S映射、文献[21]的映射TLT和所提S(L)+L映射生成的二值序列的自相关性分析结果如图7所示。

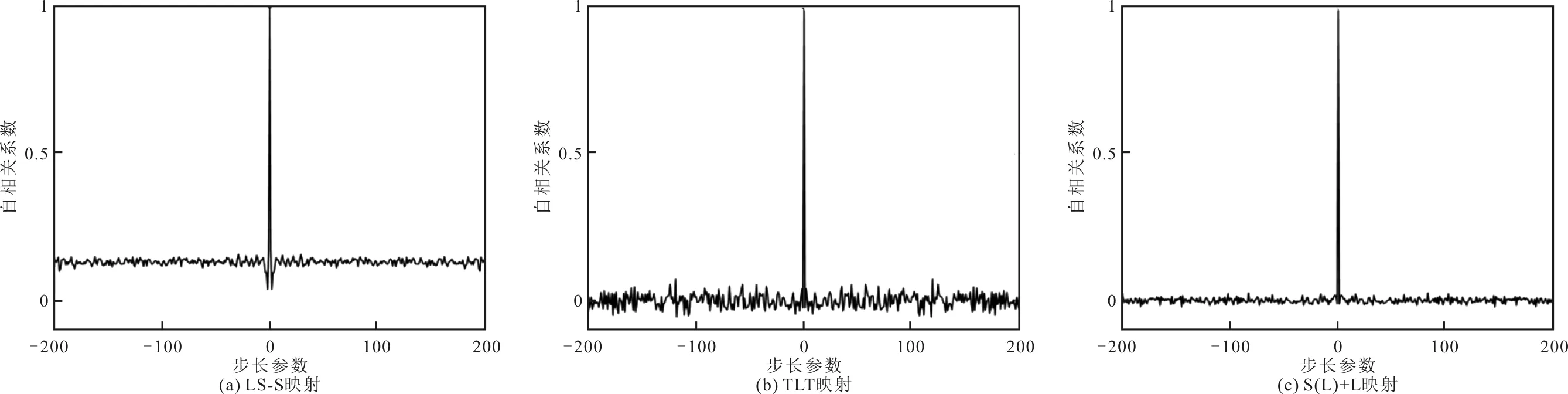
图7 3种映射二值序列自相关性仿真结果

自相关系数值与步长参数有关，当步长参数改变时，若自相关系数的改变越小，则证明二值序列的随机性能越好。从图7可以看出，当步长不为0时，LS-S映射的自相关系数位于0的上方，而TLT映射和S(L)+L映射的自相关系数均在0的附近且无限逼近，说明相比于LS-S映射，TLT映射和S(L)+L映射产生的二值序列有着更好的自相关性，其对应的二值序列随机性能更好。

3.5.2 互相关性

考查文献[20]的LS-S映射、文献[21]的TLT映射和所提S(L)+L映射生成序列的互相关性。互相关系数越逼近0，序列的随机性能越理想。设定3种映射的序列长度均为10 000，序列的初始值分别为0.4和0.5。当序列的初始值发生变化时，3种映射互相关性仿真结果如图8所示。从图中可以看出，LS-S映射生成序列的互相关系数距离0比较远，而TLT映射和S(L)+L映射生成序列的互相关系数均接近于0，说明相比于LS-S映射，TLT映射和S(L)+L映射生成的混沌序列具有较高的随机性能。

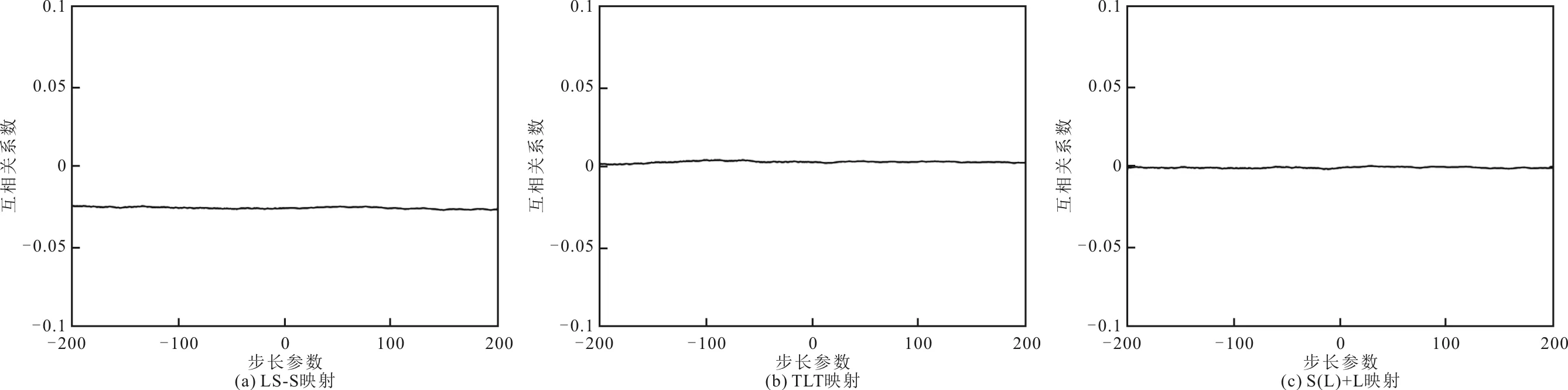
图8 3种映射互相关性仿真结果

3.6 平衡度

将混沌映射的实值序列经二值化处理得到二值序列，定义序列平衡度的计算表达式[23]为

(11)

式中：N为序列长度；p和q分别表示序列中0和1出现的次数。

E越小，说明序列中p和q越接近，从而说明序列随机性越理想[23]。设定混沌映射序列的N=10 000，初始值x0由0到1。文献[20]的LS-S映射、文献[21]的TLT映射和所提S(L)+L映射产生序列的平衡度分布情况如图9所示。从图中可以看出，文献[20]中LS-S映射产生二值序列的平衡度位于0.2附近，而文献[21]中TLT映射和所提的S(L)+L映射的平衡度都位于0的附近且无限逼近于0。说明相较于LS-S映射，TLT映射和所提S(L)+L映射的平衡度较好。

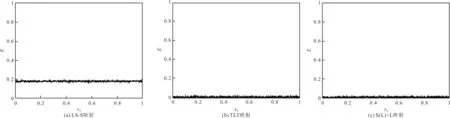
图9 3种映射的平衡度分布

3.7 初值敏感性

初值敏感性反映混沌系统的不可预测性能。设定相同的系统参数，对于初值发生微小的变化，分岔情形出现早的序列，对应映射的初值敏感性就越好。

设定初始值x0=0.40，变化值Δx=10-15，生成序列长度分别取1,2,…,20。文献[20]的LS-S映射、文献[21]的TLT映射和所提S(L)+L映射的初值敏感性仿真结果如图10所示。图10显示，当序列长度取20时，LS-S映射没有出现分岔情形；TLT映射在长度为9时出现了分岔情形；S(L)+L映射在长度为3时就出现了分岔情形。说明在系统参数设定相同的情况下，所提的S(L)+L映射比文献[20]提出的LS-S映射以及文献[21]中提出的TLT映射出现分岔情形更早，具有更好的初值敏感性。

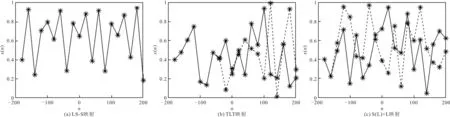
图10 3种映射的初值敏感性仿真结果

3.8 位变化率

位变化率从另一个侧面反映混沌序列的初值敏感性，一般认为，若位变化率接近50%，则表明映射具有较理想的初值敏感性[23]。设定生成序列长度N=10 000，初始值变化值Δx=10-15。文献[20]的LS-S映射、文献[21]的TLT映射和所提S(L)+L映射的位变化率仿真结果如表2所示。

表2显示，TLT映射和S(L)+L映射比LS-S映射的位变化率更接近50%，说明相较于文献[20]的LS-S映射，文献[21]提出的TLT映射和所提的S(L)+L映射对初始值的变化更敏感。

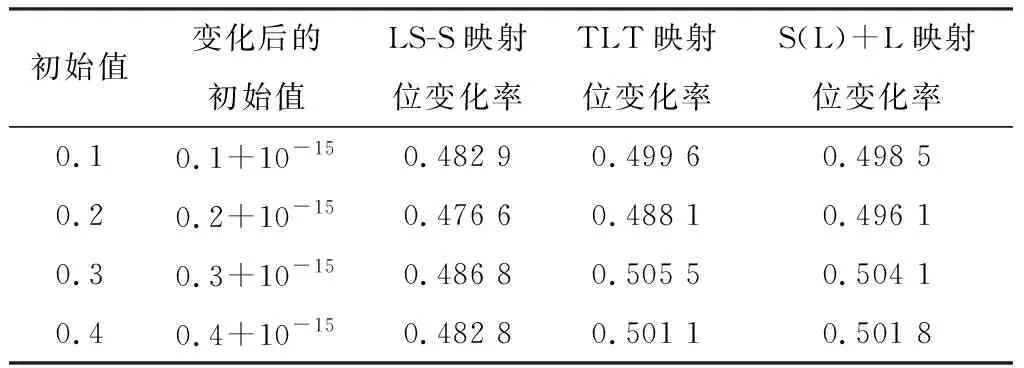
表2 3种映射生成序列的位变化率仿真结果

4 结语

提出一种改进的一维复合混沌系统。该复合混沌系统以Logistic和Sine映射作为种子映射，复合、组合生成不同的混沌映射。与经典一维混沌系统以及文献[20]、文献[21]提出的一维复合混沌系统相比，扩展了混沌系统参数个数，改善了混沌区间小、混沌区间不连续、生成序列随机性差以及初值敏感性差等问题，另外，生成的混沌映射保留了底层映射的参数取值范围，可以直接取代底层映射应用于图像加密中。下一步要做的工作主要是，如何在不降低安全性的前提下，改善在此复合混沌模型，提高计算效率。