基于各向异性高斯滤波器的改进引导滤波算法

王富平，齐明辉，吉聪聪，岳 兵，李 藕，刘卫华

(西安邮电大学 通信与信息工程学院，陕西 西安 710121)

图像边缘特征是图像中最稳定的特征之一，是人眼最为关注的信息源，因此，更为精准地检测到图像的边缘对于后续图像处理至关重要[1-2]。图像边缘特征属于高频信息，传统滤波方法在处理时极易导致滤波后的图像细节丢失，造成图像边缘模糊。为此，各种边缘保持滤波算法被提出，即通过图像的空间信息对图像的非边缘区域进行平滑，最大程度地保留图像的边缘结构[3-5]。图像边缘保持滤波算法被广泛应用于不同的图像处理领域，如图像匹配[6-8]、角点检测[9-12]、雾霾去除[13]及上采样等。

目前，已有的边缘保持滤波算法主要分为基于全局的边缘保持滤波[14-15]和基于图像局部的边缘保持滤波算法[16]。基于全局的滤波算法是通过求解基于整幅图像的最优化结果达到最终的滤波结果，但此类算法的计算复杂度高且计算量较大。基于图像局部结构的边缘保持滤波算法最为经典的是双边滤波算法[17]，其主要思想是利用目标像素的局部区域内其他像素的加权平均值代替目标像素，并利用周边区域像素与目标像素间的灰度差和欧式距离生成自适应权重。该算法能够有效保留图像的边界信息并去除噪声干扰，但会导致图像局部梯度反转效果。引导滤波算法[18]可有效缓解该问题，其通过引入引导图像对需要保留的边缘进行自适应的强化提取，相比于双边滤波器有着更强的边缘保持能力。但是，传统引导滤波算法[18]中使用的矩形均值窗口，使得窗口内远离中心的其他像素容易干扰滤波，导致图像边缘两侧模糊及产生光晕伪影等现象。

为了提升传统引导滤波的边缘保持性能，提出一种基于各向异性高斯滤波器的改进引导滤波算法。将各向异性高斯滤波器与传统引导滤波算法相融合，更准确地识别图像的边缘结构。同时，基于各向异性高斯滤波器的权重因子对窗口内的像素信息进行加权融合，使其具有更好的边缘感知性，以期获得的滤波结果能够更好地抑制边缘处的模糊以及光晕等现象。

1 各向异性高斯滤波器与引导滤波

1.1 各向异性高斯滤波器

各向异性高斯滤波器[19-20]具有较强的边缘分辨力，被广泛应用于图像边缘检测中。为了增强传统引导滤波算法的边缘保持性，利用各向异性高斯滤波器作为感知窗口。各向异性高斯滤波器gσ,ρ(m)是两个互相垂直方向不同尺度的一维高斯滤波器的卷积，可表示为

(1)

式中：σ为各向异性高斯滤波器的尺度；ρ为各向异性因子；m为像素位置。

对gσ,ρ(m)滤波器进行旋转，可得到一组沿不同方向的θ的各向异性高斯滤波器，即

gσ,ρ,θ(m)=gσ,ρ(Rθm)

(2)

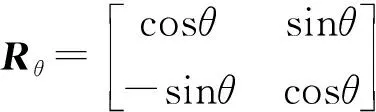
对于各向异性高斯窗来说，该窗口的噪声抗干扰性和各向异性高斯滤波器的尺度σ呈正相关的关系。各向异性因子ρ与滤波器的边缘感知精度相关。各向因子影响了各向异性高斯滤波器的窗口形状，即ρ越大时滤波器窗口的形状更狭长，能够较好地与图像边缘结构信息保持一致，而随着ρ减小，滤波器窗口的空域范围也会随之减小，导致滤波结果的方向一致性变差和边缘定位误差变大。当参数σ=ρ=6时，8个方向的各向异性高斯窗口如图1所示。

图1 8个方向的各向异性高斯窗口

由各向异性高斯滤波器gσ,ρ(m)产生的各向异性高斯滤波器窗口和滤波器权重分别为

Nm,θ={m|gσ,ρ,θ(m)>γ}

(3)

wm,θ={gσ,ρ,θ(m),m∈Nm,θ}

(4)

式中，γ为阈值，设置γ=0.000 1。

1.2 基于各向异性高斯滤波器的改进引导滤波

在传统引导滤波中，将引导图像I作为输入图像p的约束条件，对输入图像进行优化滤波，最终得到边缘保持的引导滤波结果[18]。但是，传统引导滤波采用的滤波窗口是矩形窗口，当图像边缘像素处于窗口中心时，窗口内距离中心较远的像素会干扰边缘像素滤波，影响图像的边缘保持性。为了解决传统引导滤波的不足，基于各向异性高斯滤波器的改进引导滤波，结合图像边缘结构特性和各向异性高斯滤波器的方向选择性和自适应加权性，根据图像中边缘方向自适应选择对应的各向异性高斯滤波器，从而适应不同方向边缘的有效滤波，保证定位准确度和边缘保持性。

Nm,θ为目标像素位置m处产生方向为θ的各向异性高斯滤波器的窗口，假设输出图像q与引导图像I在该窗口Nm,θ上为线性关系，则可以表示为

qn=amIn+bm,∀n∈Nm,θ

(5)

式中，qn和In分别表示输出图像q与引导图像I在像素位置n处的值，n为窗口Nm,θ的像素位置。am和bm分别表示窗口Nm,θ范围的增益系数与偏差系数。为了提高边缘识别的精确性，在传统引导滤波的平方误差损失函数中增加各向异性加权因子wn,θ，对局部窗口内滤波结果和输入图像之间的误差进行空域加权约束。基于各向异性高斯窗口的改进引导滤波的目标函数为

(6)

式中，ε是正则化参数，可以抑制am过大。

利用最小二乘法求解目标函数E(am,bm)的最优解，分别可得

(7)

(8)

(9)

(10)

(11)

进而，对局部滤波窗口内已获得的线性参数am和bm进行局部加权操作，分别可得

(12)

(13)

最终得到方向为θ的图像引导滤波结果为

(14)

滤波窗口有多个方向，将滤波方向进行离散化，且离散方向个数K=8，则第k个滤波器的方向为

(15)

那么，第k个方向上的滤波结果为

(16)

接下来，从多个方向的高斯窗的滤波结果中选择最接近输入图像的结果作为最佳的滤波结果，表示为

(17)

最后，利用qs代替输入图像，经过多次滤波处理后就得到了最终的滤波结果qo，即

qo=qs

(18)

将各向异性高斯滤波器融入传统引导滤波目标函数，使其具有更好的边缘感知，同时对局部线性参数am和bm进行各向异性加权，使得最终输出qo具有更好的边缘保持效果。

2 实验结果与分析

2.1 算法参数设置

基于各向异性高斯滤波器的改进引导滤波算法主要包含尺度σ、各向异性因子ρ和滤波器方向数K等3个参数。当σ=ρ时，各向异性高斯滤波器的噪声抑制性和方向分辨性综合最优[21]。在不同尺度参数下，分别对200张花卉图片[22]进行滤波处理，并计算与原图像的结构相似性指数(Structural Similarity,SSIM)，不同尺度下花卉图的SSIM平均值如图2所示。可以看出，当σ=ρ=3时，SSIM平均值最大，因此，可在改进算法中将尺度和各向异性因子设置为3。

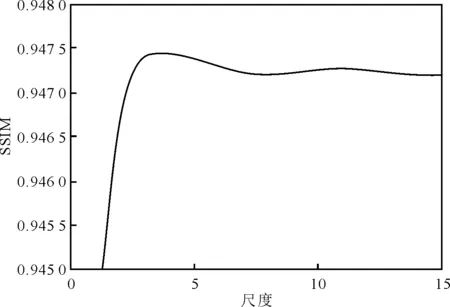
图2 不同尺度下花卉图的SSIM平均值

2.2 精细边缘保持性评价

改进算法对精细的边缘有着较好的保持效果。为了验证改进算法的边缘保持性，分别对比改进算法和传统引导滤波[18]对不同分辨率边缘的滤波效果，如图3所示。理想边缘条纹图由黑白间隔的竖直条纹顺序排列而成，黑色条纹宽度设置为10个像素，白色条纹的宽度在区间[1,49]上以1像素逐渐增加。由图3可以看出，两个虚框处分别标识了改进算法和传统引导滤波初次达到理想边缘值时的边缘，且此时理想边缘宽度分别是dw=11和dw=45，表明改进算法能够识别更精细的边缘。随着白色条纹的边缘变宽，两种算法的滤波结果会接近并最终到达理想的边缘线上。

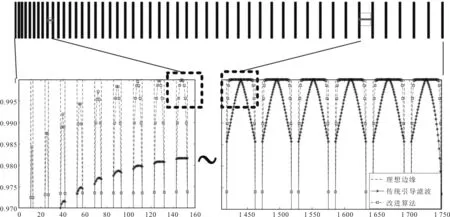
图3 两种算法的滤波结果对比

为了进一步对比，将图3中标识的边缘局部区域放大，如图4所示。其中，图4(a)为dw=11时，两种算法到达理想边缘值时的滤波响应，图4(b)为dw=45时，两种算法到达理想边缘值时的滤波响应。

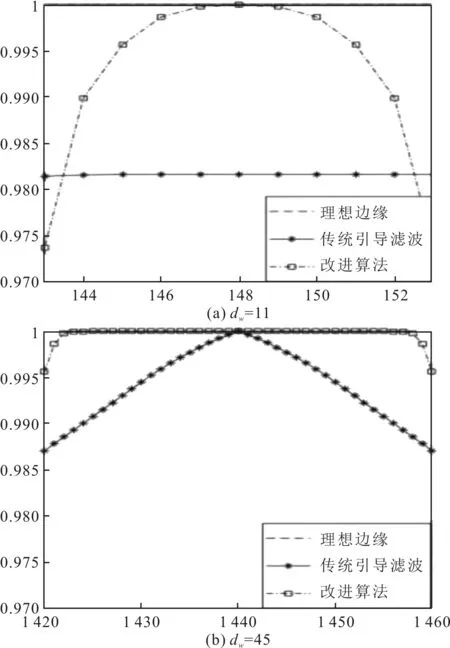
图4 标识边缘的局部放大图

由图4可知，改进算法比传统引导滤波能够更快地到达理想边缘值，表明改进算法对精细边缘的检测能力更强。

2.3 图像平滑处理结果对比

图像平滑处理是常用的图像预处理步骤，对后续的图像处理效果产生重要的影响。通过组合不同的参数ε和r，分别使用传统引导滤波[18]和改进算法对图像进行平滑处理实验，结果分别如图5和图6所示。

图5 传统引导滤波的平滑结果

图6 改进算法的平滑结果

由图5和图6可以看出，随着ε和r的增大，平滑图像会逐渐模糊。相比于传统引导滤波，改进算法的平滑结果在边缘处更清晰，说明改进算法在图像平滑处理中的边缘保持性更好。

为了更加客观地对改进算法的性能进行评估，在2 000张花卉图像[22]和BSD 500数据集[23]上进行平滑处理。其中，花卉图像中花瓣具有丰富的纹理边缘信息，能够很好地反映出算法的边缘保持能力，而BSD 500数据集包含多种类型图像，能够验证算法对于不同图像特征进行滤波的鲁棒性。实验分别计算两种算法在2 000张花卉图像和BSD 500数据集上，不同参数ε和r时的SSIM平均值，结果分别如表1和表2所示。SSIM平均值越大表示算法的边缘保持能力越好。

表1 两种算法在不同滤波下的SSIM平均值对比

表2 两种算法在不同滤波下的SSIM平均值对比

可以看出，改进算法的SSIM平均值比传统引导滤波要高，证明了改进算法相较于传统引导滤波算法能够更好的保留图像边缘，并且具有较好的鲁棒性。

2.4 图像细节增强结果对比

图像的细节增强[24]是图像处理中一个比较重要的应用，能够增强图像中的物体边缘处的细节，使图片提供更多的信息。图像细节增强公式为

IEnhanced=q+α(p-q)

(19)

式中：q表示输入图像；p是平滑后的结果；α是增益系数。

实验中传统引导滤波和改进算法参数设置相同，即r=16、ε=0.12和α=7。传统引导滤波[18]和改进算法的增强结果对比如图7所示，图7(a)为原始图像和局部放大图像。由图7可以明显看出，相较于原图，传统引导滤波增强后的图像的光晕伪影有所减少，但部分的细节边缘处仍然较为模糊，增强效果不理想。改进算法增强后的图像边缘更为清晰，视觉质量较好。这是因为改进算法的各向异性高斯窗是狭长的，具有较好的方向选择性，在进行滤波处理的时候可以自动选择最接近图像边缘方向的滤波器，能够有效抑制边缘周边干扰。因此，改进算法的边缘增强效果更佳。

图7 两种算法的增强结果对比

2.5 图像的亮度调整结果对比

图像的亮度调整处理一般用来增强低光照下的图像，使得低亮度图像的内容变得更符合人眼的感知。以往的图像亮度调整通常只对图像的单个像素的像素值进行调整，没有考虑到图像的局部结构信息，经过亮度调整的图像会出现过曝光现象。因此，实验将传统引导滤波[18]和改进算法应用到图像亮度增强，能够有效的保持原图像的边缘结构，具有较好的亮度增强效果，具体步骤如下。

步骤1利用滤波算法对输入图像进行平滑得到平滑后的图像，将图像与平滑图像相减后得到细节层图像。

步骤2利用伽玛校正[23]的方法对平滑图像进行扩展，得到扩展后的亮度图像。

步骤3将图像的细节层与扩展后的亮度图像合并得到最后的亮度调整结果。

传统引导滤波[18]和改进算法的亮度调整结果对比如图8所示，图8(a)为原图像以及部分局部放大部分。

图8 两种算法亮度调整结果对比

由图8可以看出，传统引导滤波有效地提升了原图像的亮度，但从局部放大部分看，仍然存在部分模糊和颜色失真等现象。而改进算法的调整结果较好，细节部分较为清晰，图像中“门”与“墙”间的界限分明，边缘细节保持效果很好。因此，改进算法在图像对比度的调整效果也是优于传统引导滤波。

3 结语

基于各向异性高斯滤波器的改进引导滤波算法，利用各向异性高斯滤滤波器较强的边缘感知性，将各项异性高斯窗及其加权特性融入传统引导滤波框架，能够有效增强算法的边缘保持性。实验结果表明，相较于传统引导滤波，改进算法的边缘感知性有了较大的提升。在图像平滑、图像增强以及图像亮度调整等方面也能够更好地保留图像的边缘，有效减少了伪影、边缘模糊等现象。