基于MDP的协作认知边缘计算网络资源分配方案

刘伯阳，马 杰，白 静,万奕尧

(西安邮电大学 通信与信息工程学院，陕西 西安 710121)

移动通信技术发展迅速，短短几十年间已经由以模拟通信技术为主的第一代移动通信系统(1st Generation Mobile Communication System，1G)发展到目前广泛使用的以正交频分复用(Orthogonal Frequency Division Multiplexing，OFDM)技术、多输入多输出(Multiple Input Multiple Output,MIMO)技术为核心的第四代移动通信系统(4th Generation Mobile Communication System，4G)。第五代移动通信系统(5th Generation Mobile Communication System，5G)目前已经在部分城市进行布设，相比于4G，5G具有更高的传输速率与更低的网络时延。随着5G的逐渐成熟，一些新业务如虚拟现实(Virtual Reality,VR)、增强现实(Augmented Reality,AR)和在线大型移动游戏等将逐渐向无线终端侧部署。然而，此类型业务具备高计算复杂度与低时延两个共同点。移动终端由于计算资源限制导致计算能力较弱，难以独立按时完成上述业务。

移动边缘计算技术(Mobile Edge Computing,MEC)是一种计算辅助技术[1]。与云计算类似，MEC允许用户将待计算数据卸载至服务器侧，服务器进行计算后将结果返回。但是，边缘计算与云计算不同，云计算中用户上传待计算数据前需要通过互联网层层请求，时延较长，难以满足业务低时延要求。MEC将服务器下沉至网络边缘，相比于云计算，MEC更靠近用户侧，用户可与MEC服务器建立无线链路直接进行数据交互，大幅度缩减数据上传与计算结果下载时延，满足用户业务低时延的要求。

由MEC的原理可知，移动用户能进行MEC的关键要素是频谱与能量，用户需耗费一定的能量将任务通过可用频谱将待计算数据卸载至MEC服务器。然而，目前移动设备数量巨大，据统计，仅无线物联网设备数量已经达到2 000多亿，且仍在快速增长。更为严峻的是，目前适合通信的频谱几乎都被分配殆尽，为如此海量的设备分配专用频谱几乎不可能。

认知无线电(Cognitive Radio，CR)技术是一种动态频谱接入技术，其允许网络中的次用户(Secondary User,SU)即未授权用户根据主用户(Primary User,PU)即授权用户的状态调整自身发送参数接入PU频谱，实现频谱共享，为SU提供更多的频谱接入机会[2]。另外，移动终端受其尺寸限制，难以装配大容量电池，电量有限，续航能力较弱，若长时间进行高复杂度业务计算将耗费大量能量，大幅度缩短续航时间，严重影响用户体验。能量收集(Energy Harvesting,EH)技术允许移动用户吸收周围环境能量，如太阳能、电磁能等，提升能量供应水平，延长续航时间[3]。因此，可将CR、EH与MEC技术进行结合，研究协作认知EH-MEC系统，为用户提供能量供应、频谱接入与业务计算服务。

目前，已有一些关于EH、CR与MEC分别结合的研究。文献[4]研究了无线充能MEC系统，通过优化卸载策略，即是否进行卸载以及MEC计算参数，最大化多个用户计算速率之和。文献[5]将上述场景扩展到多天线领域，利用小基站对用户进行无线充能，在满足业务需求的前提下最小化小基站能耗。文献[6]将无线充能场景进一步拓展到空域，采用无人机辅助MEC系统，无人机充当无线基站，通过优化系统参数最大化其计算速率。然而，上述文献并未考虑到移动边缘计算网络中的频谱稀缺问题，在频谱资源受限的实际应用场景中，性能将急剧下降。

作为一种有效缓解频谱稀缺问题的技术，近年来关于CR的MEC系统也得到一些研究。文献[7]提出了一种基于CR的MEC系统，在满足PU干扰容限的限制下最大化系统效益。文献[8]提出一种三层CR-MEC网络架构，CR用来为网络用户挖掘空闲频谱以提供频谱接入机会。但该研究只提出框架并未进行详细的研究。文献[9]与文献[10]对无线充能的CR MEC系统进行了研究，分别针对PU与SU协作与非协作的情况，通过优化SU操作参数最大化计算能量效率与计算比特数。但是，上述文献只考虑了系统的短期优化，对于长期计算任务而言，能够取得的收益有限。

值得注意的是，目前关于MEC与CR-MEC的研究均集中在单个时隙对用户进行性能优化的场景，即瞬时优化场景。但在无线通信网络中，单个时隙性能对整个网络性能的影响不大，网络更关注长期性能收益，且单个时隙性能最优不等于长期性能最优。因此，拟提出一种协作认知EH-MEC系统中的资源优化方案，未授权用户通过与授权用户进行协作以获取能量与频谱接入机会。利用强化学习中的马尔可夫决策过程(Markov Decision Process,MDP)对协作认知EH-MEC系统进行长效性能优化。以长期计算任务量为收益，通过对未授权用户的EH时间长度、CPU计算频率、任务卸载功率以及MEC模式进行优化设计使得未授权用户获得的长期计算量最大化，并验证所提方案的正确性与有效性。

1 系统模型

考虑协作认知EH-MEC系统模型，包括一个主用户发送端(Primary Transmitter,PT)，一个主用户接收端(Primary Receiver,PR)、一个SU以及一个搭载了MEC服务器的无线接入点(Access Point,AP)。各节点都受到高斯白噪声的影响，为表示方便且不失一般性，假设各节点处噪声功率均为σ2。用hp、hs、gp与gs分别表示PT与PR之间、PT与SU之间、SU与PR之间以及SU与AP之间的信道功率增益。假设所有节点均装备单天线且工作在同步的时隙结构下，令T表示单个时隙长度。设信道相干时间是时隙长度的整数倍，即Tcoh=ΘT，为Θ≥1的整数，在信道相干时间Tcoh内，信道功率增益保持不变。具体的协作认知EH-MEC系统模型如图1所示。

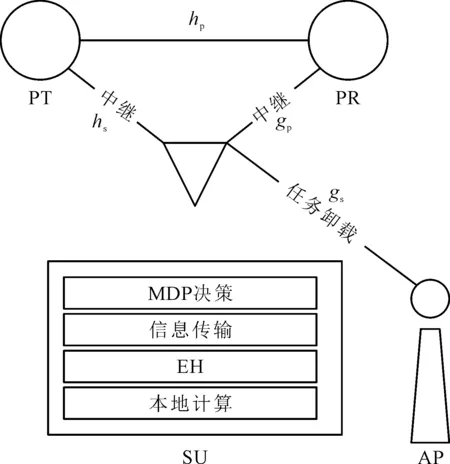
图1 协作认知EH-MEC系统

PT一共有忙碌状态与空闲状态两个状态，分别用A与S表示。与文献[11-14]相同，假设PT的状态变化可建模为一个二状态马尔科夫链，如图2所示，其中Pi,j表示状态转移概率，i,j∈{A,S}。

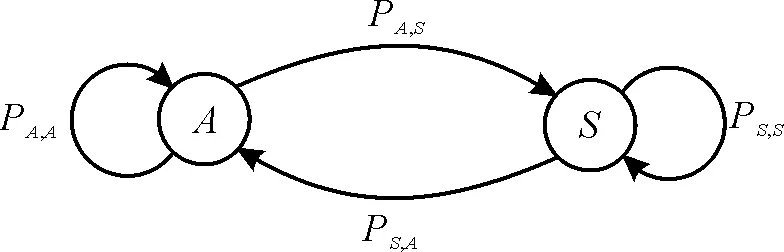
图2 PT状态转移

假设PT在忙碌状态时具有rp比特的数据要发送，且需占用整个时隙，PT的发送速率为

(1)

式中：pp为PT发送功率；W为信道带宽；σ2为噪声功率。

2 问题建模

用MDP对SU行为进行优化,MDP包含状态、行为、奖励与策略等4个模型要素。下面分别根据模型对上述元素进行分析。

1)状态。对研究的模型来说，SU知道PT当前准确的PT状态，MDP在时隙t的状态可以表示为st=(θt,es,t)。其中：θt∈{A,S}；es,t为时隙t起始时SU可用的能量值。

2)行为。在时隙t下SU有3种选择，用βt表示：βt=0时，SU不进行任务计算；βt=1时，SU只进行本地计算；βt=2时，SU与PT进行协作中继，协助PT发送完数据后采用部分卸载机制进行MEC。同时，SU可在PT进行数据发送时通过接收PT发送信号进行EH，令τt表示时隙t下SU进行EH的时间，SU吸收的能量表达式为

eh,t=φpphsτt

(2)

式中：φ为EH的效率；hs为信道增益。

SU进行MEC需耗费能量，因此SU每个时隙拟投入的能量也需进行决策。基于此，在时隙t下行为表示为αt=(τt,ea,t,βt)，其中，ea,t表示SU拟投入的能量值。

3)奖励。考虑目标是最大化SU长期的计算任务量，因此MDP在时隙t获得的奖励为时隙t下SU执行MEC进行的任务量，记为R(st,at)。奖励是状态和行为的函数，在不同的状态和行为下奖励取值不同，下面分别进行分析。

情况1当st=(A,es,t)，at=(τt,0,0)时，即当PT处于忙碌状态，且SU不进行任务计算，只进行EH的情况。此种情况下，SU不获得任何奖励，但是能量会得到补充，即

R(st,at)=0

(3)

令eu,t表示SU收集的能量

eu,t=min(φpphsτt,emax)

(4)

则SU可用能量更新为

es,t+1=min(es,t+eu,t,emax)

(5)

式中，emax为SU电池最大容量。

情况2当st=(A,es,t)，at=(τt,ea,t,1)，即当PT处于忙碌状态，SU进行EH，并投入ea,t能量进行本地计算。投入ea,t后SU能获得的奖励与SU的CPU频率有关，在投入ea,t后需优化SU CPU工作频率。CPU最优工作频率的表达式为

(6)

式中：η为SU每个CPU周期耗能功率系数。设C为SU计算1 bit数据需要的CPU周期数。SU可获得的奖励为

(7)

SU可用能量更新为

es,t+1=max[min(es,t+eu,t,emax)-ea,t,0]

(8)

情况3当st=(A,es,t)，at=(τt,ea,t,2)，即当PT处于忙碌状态，SU进行EH，并投入ea,t能量与PT进行协作中继，协助PT将待传数据传输完毕后采用部分卸载方式进行MEC，如图3所示。

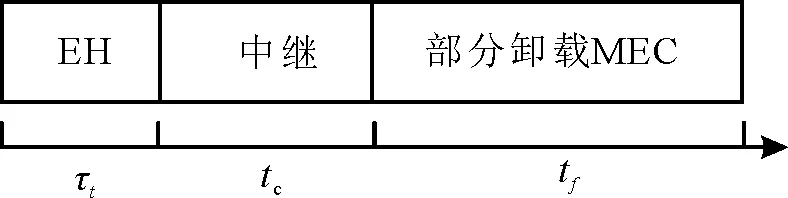
图3 st=(A,es,t)，at=(τt,ea,t,2)SU操作示意图

SU采用放大转发的方式进行协助PT中继传输数据，令tc表示协作时间。在[τt,τt+tc/2]时间段内，PT发送信息给PR与SU，PR与SU接收的信号分别为

(9)

(10)

式中，ns与np分别为PR与SU处的噪声。在[τt+tc/2,τt+tc]内，SU将接收的信息转发给PR，PR收到的信号为

(11)

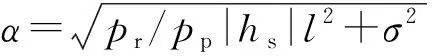
(12)

(13)

为后续计算方便，令pr=pmax，也可以对pr进行线性一维搜索得到最优值。

协作中继传输结束后PT频谱空闲，SU接入进行任务卸载时，SU可用于MEC的能量为

(14)

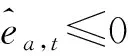
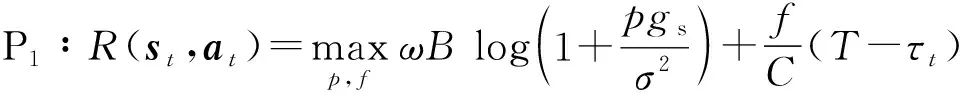
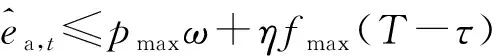
(15)

其中，

(16)

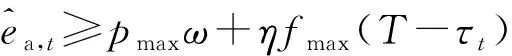
情况4当st=(S,es,t)，at=(0,ea,t,1)，即PT处于空闲状态，SU不进行EH，投入ea,t能量进行本地计算。最优CPU频率与获得的奖励分别为

(17)

(18)

能量更新与式(4)和式(8)相同。

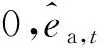
除了以上情况外，其余3种情况下均将奖励设置为R(st,at)=-c，其中c>0，即若出现以下几种情况，SU将获得负奖励。因此，在决策过程中，SU将会尽量避下述情况的出现。

情况1SU打算投入的能量超过SU可用能量的情况,表达式为

ea,t>min[es,t+min(φpp|hs|2τt,emax),emax]

也即违背能量因果限制的情况。

情况2当PT处于空闲状态S且βt=0，即PT处于空闲状态时SU不进行任何计算的情况。

情况3当PT处于空闲状态S且τ>0时，即PT处于空闲状态时SU仍打算进行EH的情况。

4)策略。策略是行为与状态之间的映射关系，记为π(at|st)，表示在当前状态为st的情况下选择行动at的概率，策略可以认为是系统状态与选择的行为之间的映射关系。考虑确定性策略，即对于状态st，SU将以概率1选择行为at。

MDP的目标是寻找最优策略最大化长期期望收益Vπ(st)，优化目标是最大化相干时间ΘT内SU的期望收益，其表达式为

(19)

其中，

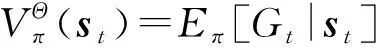
式中，γ为折扣因子。γ表示未来收益与当前收益的比重，是SU对当前动作所能带来的未来收益的重视程度。γ越大表示SU对未来收益越重视，越小则表示SU更注重当前就近时隙的收益。通过对Bellman方程的求解可获得最优策略为

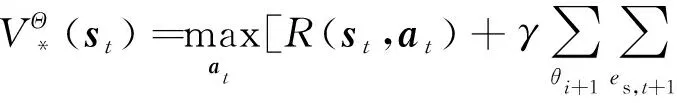
(20)

其中，

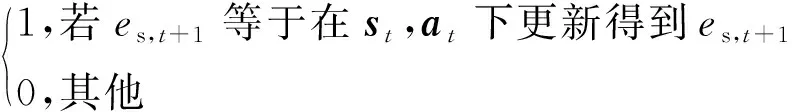
(21)

上述Bellman方程可通过值迭代或策略迭代 的方式进行求解。

3 性能仿真及分析

利用Matlab软件对所提方案进行计算机仿真，默认参数设置如表1所示。行为空间为连续空间，在进行MDP值迭代或策略迭代时难以计算。因此，仿真前必须将连续参数进行离散化处理。以eh为能量粒度，ea,t、es,t取值空间为

表1 仿真参数

其中，ea,t,num与es,t,num均为整数。EH时间τt也需进行量化，将EH时间在[0,T]内进行均匀量化，划分为τnum+1个时刻值。

考虑折扣因子γ以及相干时间时隙数Θ对SU期望计算量(每个时隙的平均计算量)的影响，对SU期望计算量与折扣因子γ以及相干时间时隙数Θ的关系进行了仿真，具体如图4所示。

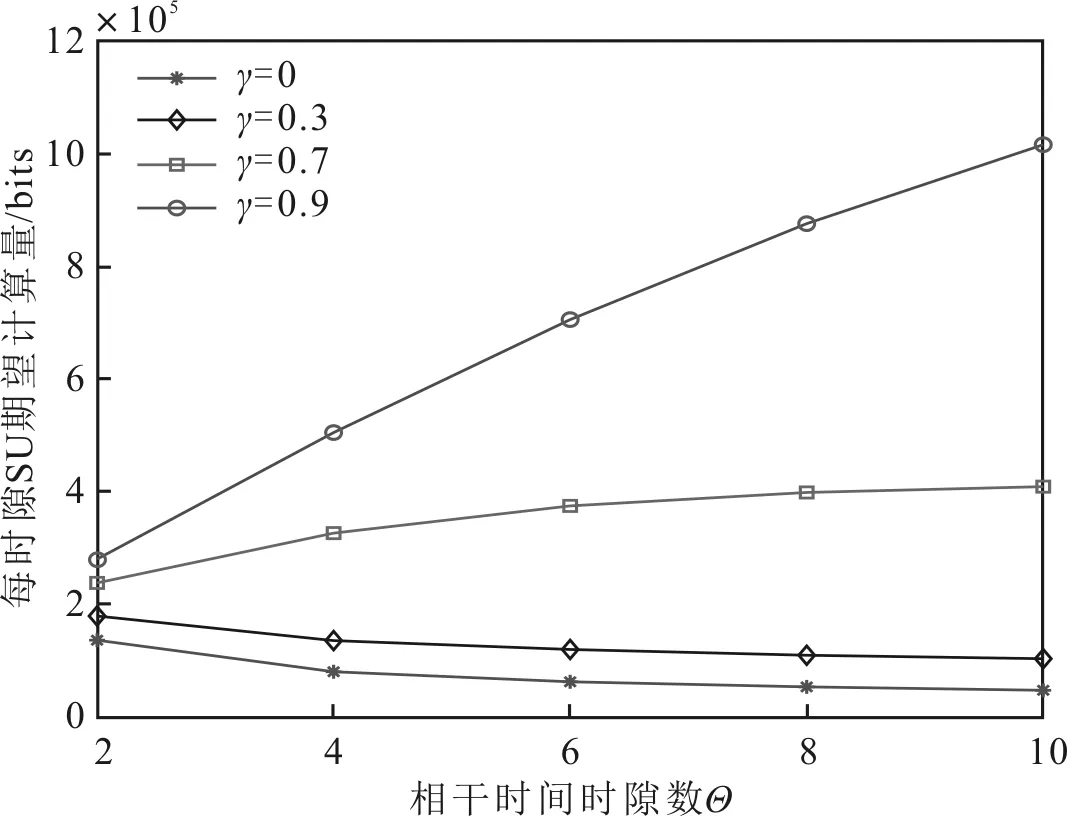
图4 每时隙SU期望计算量与γ及与相干时间时隙数Θ关系

由图4可以看出，在给定Θ的条件下，SU期望计算量随着折扣因子γ的增加而增加。折扣因子反应了SU对未来收益的看重程度，γ越大则SU在决策时会更看重未来的收益，因此随着γ增加SU期望计算量亦增加。在γ较小时SU期望计算量随着Θ增加而减小，γ较大时SU期望计算量随着Θ增加而增大，其由折扣因子的本质决定，折扣因子小则SU主要考虑当前时隙情况，折扣因子大则考虑更为长远。

为了说明系统最大可用计算、通信资源对SU期望计算量的影响，对SU期望计算量与fmax与pmax的关系进行了仿真分析，具体如图5所示。

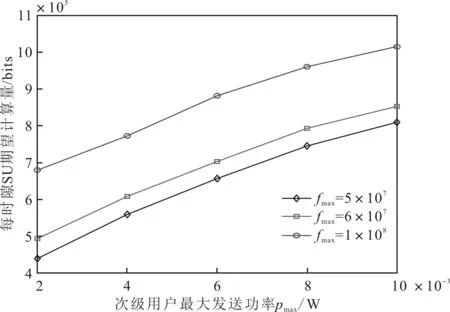
图5 每时隙SU期望计算量与fmax和pmax的关系

由图5可以看出，SU期望计算量随着fmax与pmax增加而增加。fmax与pmax增大，SU将具有更高的决策自由度，从而提升了SU的期望计算量，也能间接地证明所提算法的正确性。

同时，为了进一步研究转移概率对SU期望计算量的影响，图6对SU期望计算量与转移概率PA,A与PS,S的关系曲线进行了仿真。

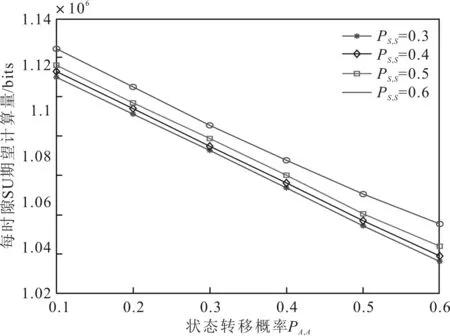
图6 每时隙SU期望计算量与转移概率PA，A和PS，S的关系

由图6可以看出，随着PA，A与PS，S的增大，SU期望计算量分别下降与增加。这是因为PA,A增加表示PU将有较大的概率处于忙碌状态，SU有较少的频谱接入机会，PS,S增加则表示PU将更多的保持空闲状态，SU将有更多的频谱接入机会。

4 结语

为了缓解移动边缘计算网络中用户设备的续航能力差，以及网络中面临的频谱资源稀缺问题。将EH、协作中继、CR与MEC相结合构成可认知EH-MEC网络架构，提出了一个长期收益最大化资源分配方案。利用MDP对SU策略进行优化设计，仿真结果表明，所提方案与各系统参数之间的关系，证明了所提方案相较于传统的短期优化方案而言，能够有效提升网络的长期期望计算量。此外，所提的可认知EH-MEC架构，显著提高了网络频谱效率。