车联网中基于随机网络演算的路由算法

朱国晖，杨 瑛

(西安邮电大学 通信与信息工程学院，陕西 西安 710121)

目前，移动通信正在完成从第四代移动通信技术(the Fourth Generation of Mobile Communication Technology,4G)到第五代移动通信技术(5th Generation Mobile Communication Technology，5G)的过渡，逐渐具备移动通信功能的汽车也在不断向着智能驾驶方向发展，正处在过渡过程中的网联阶段[1]。这个阶段的核心特征是出现了基于通信的车到车(Vehicle to Vehicle，V2V)和车到基础设施(Vehicle to Infrastructure，V2I)、车到人(Vehicle to Pedestrian，V2P)的通信技术，将车与车、车与周围的万物进行连接。5G将为车到其他(Vehicle to X，V2X)提供更高的通信能力和安全性。在5G环境下，无论是基站还是移动终端，其数量都会较4G网络环境有一个较大的增长，特别是5G带来的微基站，其高密度的部署能确保网络的高度覆盖性。

在车联网场景中，车辆作为网络中的移动节点，其运动特性带来的网络高度动态拓扑性，会在一定程度上引起网络连接的不稳定性，而5G微基站的高密度部署可以很好地解决此问题，尤其是在城市场景中，基本可以保证每一个移动节点都在其覆盖范围内。但随着节点数量的增多，随之而来的是路由选择的问题，每一个携带数据需要进行转发的节点，都会有更多备选的中继节点。因此，适应于车联网环境的路由算法成为一个研究热点。

不同的路由算法会根据网络中节点与链路之间不同的具体情况，选择不同的传输路径完成数据包的传输工作。国内外已有许多研究者对不同场景和传输需求进行了研究[2]。文献[3]在车辆自组织网络场景中提出了基于路口的V2V通信方式的路由表学习与维护的算法。该算法可以提供更稳定的路由，使传输成本更低，并且避免了不必要的数据丢失情况。文献[4]提出的MADSDV算法以多代理方法和PSO优化算法相结合，提高了链路的稳定性，可以有效地降低丢包量并增加了吞吐量。文献[5]提出了以街道为中心的机会路由算法，通过建立链路模型预测链路的可用概率。该概率通过车辆活动的稳定性与车辆的状态，使用不同的链路组合传输具有较少网络资源和较高吞吐量的分组。文献[6]提出了基于模糊逻辑系统的簇首选择算法，以运动中的车辆节点作为候选中继，减少了分簇的次数，提高了簇结构的稳定性。但是，以车辆节点作为中继的路由算法会因为车辆节点的移动性而带来网络的不稳定性。

传统的路由算法并未过多地考虑当网络中数据流具有突发性特点时的网络整体的服务质量(Quality of Service，QoS)。为了能够提供更优的QoS的中继节点，考虑使用网络演算分析节点与网络性能。网络演算[6]的发展分为确定性网络演算(Deterministic Network Calculus,DNC)和随机网络演算(Stochastic Network Calculus,SNC)两个分支。DNC提供的是确定性的QoS，数据从源节点(Source Node,SN)传输到目的节点(Destination Node,DN)时满足所有预定的性能指标。确定性的QoS是基于最坏情况下的场景，预留了充足的资源，可以保证最好的服务水平，但缺点是导致了网络资源的浪费。而SNC提供的随机QoS可以看做是用户所得到的服务是以一定的概率低于期望值的，允许一些数据包不满足预定的性能指标。确定性的QoS可以看做是随机QoS中违背期望值的概率为零的特殊情况，随机QoS相较于确定QoS可以更好地提高网络资源的利用率。因此，SNC已经被广泛应用于不同的网络领域[7-13]。

为了使选择出的中继节点具有更低的网络时延与积压，拟提出一种基于SNC的路由选择算法。该算法对同一时间到达同一服务节点的数据流进行区分，分别建立服务节点对目标数据流与竞争数据流的随机服务曲线。使用SNC分析网络中节点的服务质量，并以此为依据找到性能最优的中继节点，以期降低网络时延与积压。

1 算法分析

将网络中可以为车辆节点提供服务的固定网元统称为路边单元( Roadside Unit,RSU )，携带数据的源节点SN将数据发送给距离自己最近的RSU，再由RSU选择中继，直至包含DN的RSU接收到数据。在RSU沿路铺设达到全覆盖的场景下，每个RSU都具备充分的预信息，SN将选择RSU作为中继节点进行数据的传输，这样可以避免移动中的车辆作为中继所带来的不稳定性以及在一定程度降低因多跳传输引起的时延，具体车联网场景如图1所示。

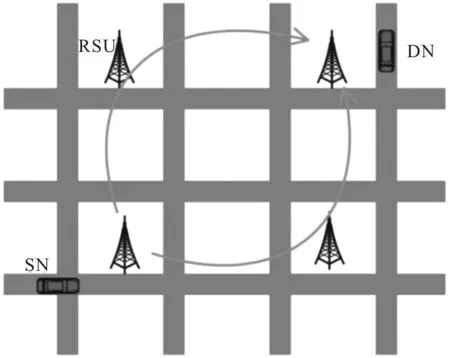
图1 车联网场景

SNC的核心思想是将网络中的数据到达流和网络提供的服务分别用随机到达曲线(Stochastic Arrival Curve,SAC)和随机服务曲线(Stochastic Service Curve,SSC)进行建模，从而分析网络的时延与积压。

1.1 数据随机到达模型分析

用非负广义递增累积函数A(t)描述数据流到达某一节点的到达过程，A(t)具有随机性与突发性。A(t1,t2)表示在时间段[t1,t2)内所积累的到达数据量，并且定义A(0)=0，A(t1,t1)=0，A(t1,t2)=A(t2)-A(t1)，0≤t1≤t2。用广义递增函数曲线α(n)表示数据流A(t)的随机到达曲线，α(n)描述了对到达网络节点的数据流的约束行为，当n=t2-t1时，α(t2-t1)为A(t1,t2)的上包络线。用A*(t)表示数据从节点的离开过程，A(t)和A*(t)均为统计独立的平稳随机过程，可以定义网络的时延与积压，如图2所示。

图2 网络的时延与积压

对于所有0≤t1≤t2，SAC满足

A(t1,t2)-α(t2-t1)≤0
A⊗β(t)-A*(t)≤0

式中，⊗为最小加卷积运算。

定义非负广义增函数f(x)和g(x)的最小加卷积⊗运算为

在确定性网络中，确定的QoS保证了网络是基于最坏情况下的场景预留足够量的资源，累积到达数据量A(t1,t2)不会超过到达曲线α(t2-t1)。但在SNC中，允许数据存在突发性，用违约变量x描述，允许A(t1,t2)-α(t2-t1)>x的情况发生，并且定义函数f(x)为α(n)的违约概率函数。

上述突发情况发生的概率受到违约概率函数f(x)的限制，对于∀0≤t1≤t2，x>0，若有概率

P{sup0≤t1≤t2{A(t1,t2)-α(t2-t1)}>x}≤f(x)

成立，则称该过程具有v.b.c(virtual-backlog-centric) SAC[14-15]，记为A(t)～sac。

假设车辆节点的数据到达过程符合泊松过程，则随机到达过程A(t)由[σa(θ),ρa(θ)]上界限制表示。其中：σa(θ)表示突发的增量；ρa(θ)表示数据流的平均速率上界。若∃θ>0,∀t1,t2≥0，则有

成立。其中：E表示期望；e为自然底数，即

E[eθA(t1,t2)]≤eθ[ρa(θ)(t2-t1)+σa(θ)]

设车辆节点到达过程服从参数为λ的泊松过程，N(t)表示t时刻到达的节点数量，则在时间段(t1,t2]内有n个节点到达的概率为

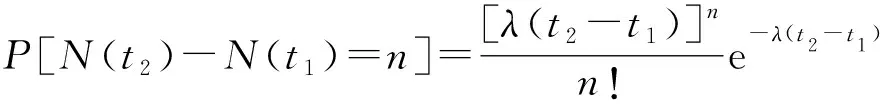
则服从泊松过程的数据流到达过程可以表示为

可得到eλ(t2-t1)(eθ-1)≤eθ[ρa(θ)(t2-t1)+σa(θ)]，即

λ(t2-t1)(eθ-1)≤θ[ρa(θ)(t2-t1)+σa(θ)]

可得到ρa(θ)=λ(eθ-1)/θ，σa(θ)=0。

由切尔诺夫不等式，可得

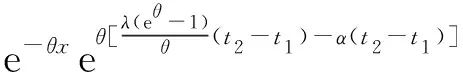
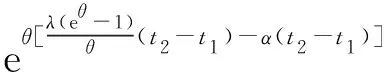
f(x)=m1e-θx

到达曲线为

式中，α(n)是关于时间间隔n的线性函数。

1.2 中继RSU随机服务模型分析

与SAC的定义类似，SSC用来表示服务节点所能提供的服务性能统计特性。网络节点所提供的随机服务曲线用广义增函数β(t)表示，当且仅当对于任意的t≥0，均满足A*(t)≥A⊗β(t)。假设违约概率函数为g(x)，在时间段(t1,t2]内，∀x≥0，系统为到达的数据提供的服务过程S(t1,t2)满足

P{β(t2-t1)-S(t1,t2)>x}≤g(x)

成立，服务系统S可为到达业务提供SSC,表示为S(t)～ssc。其中，β(t2-t1)为服务节点S(t1,t2)的下包络。系统在某时间段内累积的数据服务量S(t1,t2)比随机服务曲线β(t2-t1)小的概率受到g(x)的限制，服务曲线与服务过程如图3所示。

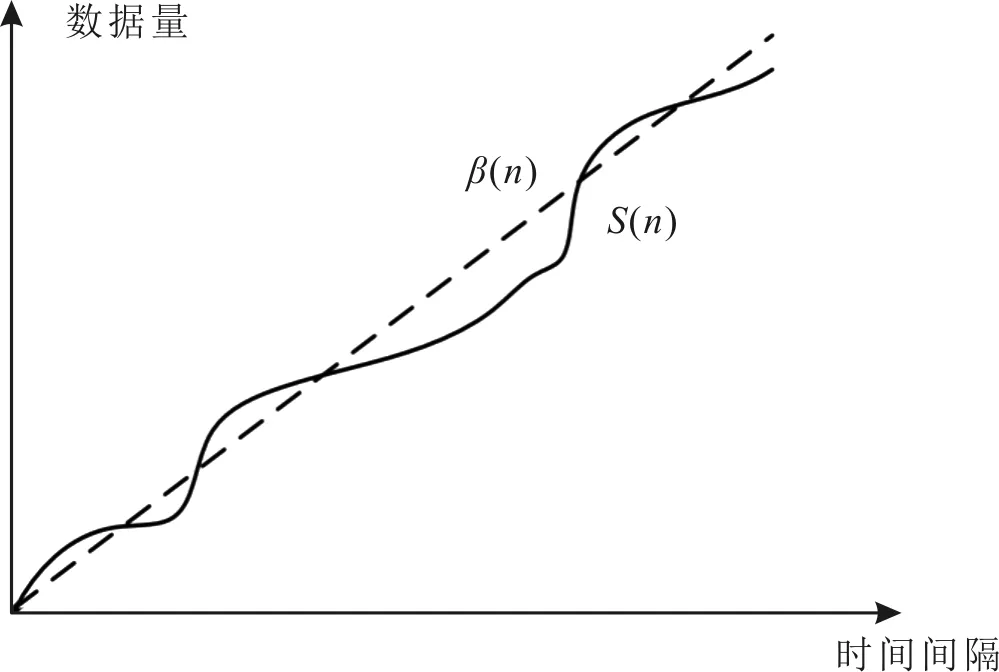
图3 服务曲线与服务过程

随机服务过程S(t)由[bs(θ),rs(θ)]下界限制表示，bs(θ)表示增量，rs(θ)表示服务平均速率下界，其表达式为

等价于

E[e-θS(t1,t2)]≤e-rs(θ)[(t2-t1)-bs(θ)]

由切尔诺夫不等式，可得

P{β(t2-t1)-S(t1,t2)>x}≤
e-θxE[eθ(β(t2-t1)-S(t1,t2))]≤
e-θxe-θ[rs(θ)[(t2-t1)-bs(θ)]-β(t2-t1)]

将e-θ[rs(θ)[(t2-t1)-bs(θ)]-β(t2-t1)]记为m2，则违约概率函数g(x)=m2e-θx。

在实际的网络环境中，服务节点对到达的数据所提供的服务也会带有一定的随机性。在绝大多数场景下的服务过程中，一个RSU会同时服务于多个车辆节点。因此，对于上述分析的数据流到达过程A(t)而言，存在与其竞争RSU服务的数据流。将与A(t)同时到达同一RSU的其他数据到达过程看作是合并后的同一数据流，并将其称为A(t)的竞争数据流到达过程，用C(t)表示，如图4所示。

图4 数据到达流与竞争流

竞争数据流到达过程同样具有随机到达曲线，若A(t)记为A(t)～sac，则竞争数据流的随机到达曲线C(t)可以记为C(t)～sac。与A(t)相类似，可以得到竞争数据流的违约概率函数和到达曲线

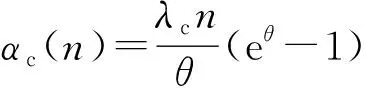
等价为

E[eθC(t1,t2)]≤eθ[ρc(θ)(t2-t1)+σc(θ)]

记竞争到达过程C(t)服从参数为λc的泊松分布，则可以得到

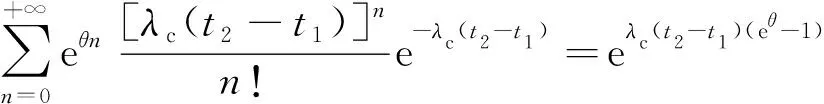
由此可得

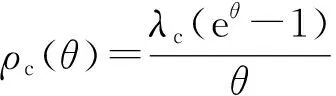
式中：ρc(θ)表示竞争数据流的平均速率上界；σc(θ)表示竞争数据流突发的增量。

设RSU对到达数据的服务速率为vc，则RSU的随机严格服务曲线可以记为β(n)=vcn。由剩余服务特性可知，假设到达系统的数据流由两条聚合流A(t)和C(t)组成，如果系统对到达的总的聚合流提供随机服务曲线满足S～，并且数据流C(t)满足随机到达曲线C～，则数据流A(t)所能获得的随机服务曲线记为

Sa～

其中,

ga(x)=g⊗fc(x)
βa=β(n)-αc(n)

得到节点对到达数据流的服务下包络线和违约概率函数，表达式分别为

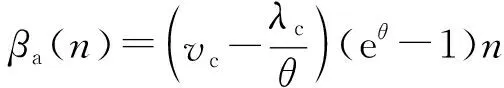
1.3 系统时延与积压分析

携带数据的车辆节点在与RSU进行信息传输的过程中，由于竞争数据流C(t)的存在，RSU对目标数据流A(t)的处理造成一定的延时与积压，导致信息传输无法达到理想状态。

找到满足随机时延P{D(t)>x}≤εd(x)和随机积压P{B(t)>x}≤εb(x)的边界函数εd(x)与εb(x)，即找到各自的违约概率函数后，使用互补累积分布函数分析边界函数，则时延D(t)和积压B(t)[16]有

根据以上分析，网络的时延与积压的表达式分别为[17]

通过以上计算过程得到节点的时延与积压的函数表达式，选择最优中继节点算法的具体步骤如下。

步骤1初始化相关信息。

步骤2发送hello数据包，并标记候选中继RSU。

步骤3建立A(t)～sac，S(t)～ssc及其违约概率函数。

步骤4选择性能最优的RSU。

步骤5判断该RSU是否为距离SN最近的RSU，如果不是，返回步骤1，如果是，则结束。

通过以上步骤选择出的RSU即为最优中继节点。

2 模型仿真与性能分析

2.1 仿真环境设置

为了验证所提算法的性能，使用Matlab仿真软件对提出的算法进行验证分析，仿真场景设置为一个SN，一个DN，多中继的场景，在保持链路连通可靠性的基础上完成仿真。

2.2 性能分析

通过将所提算法与文献[13]算法进行对比分析，得到违约概率与时延的关系，如图5所示。设Rn为源节点的数量，那么数据到达率与时延的关系如图6所示。

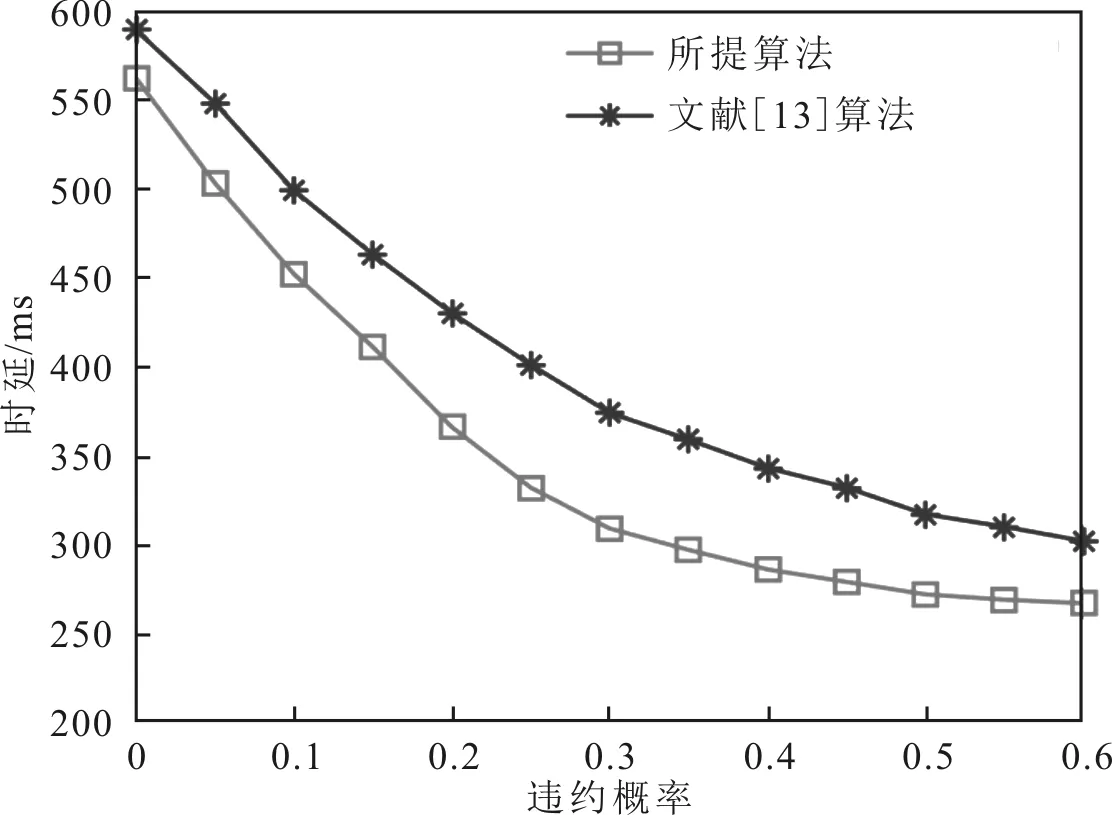
图5 违约概率与时延的关系

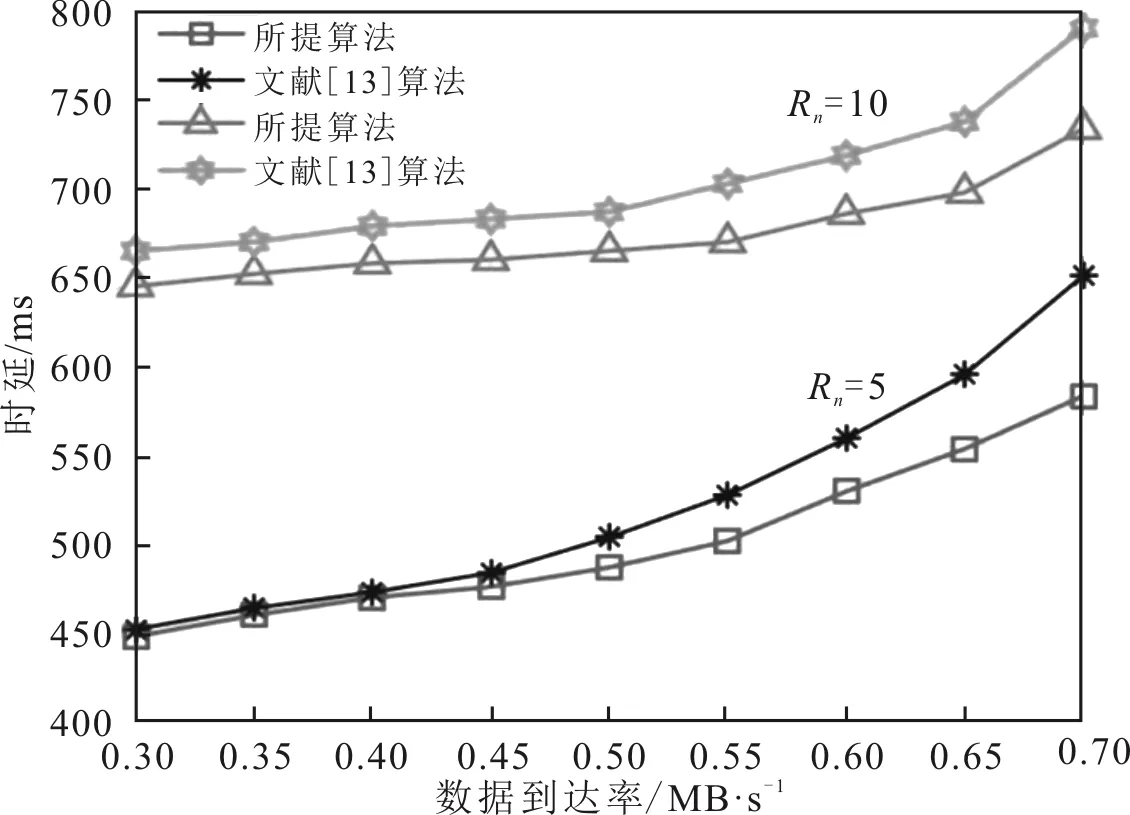
图6 数据到达率与时延的关系

由图5和图6可以看出，不同的违约概率对传输时延的影响关系，仿真中设置数据的到达率为0.5 MB·s-1。随着违约概率的增加，中继RSU对于有着突发性特点的数据的处理能力也在增强，传输时延也随之减小。在违约概率为0，即在确定性QoS的情况下，时延会达到最大。图6比较了在候选中继数量不同的情况下，SN所携带的数据的到达率与时延的关系。随着数据到达率的增加，系统的传输时延会增大。在中继数量一定的情况下，较高的数据到达率会引起RSU负载的增加。同时，会带来时延。考虑随着RSU部署密度的增加，会使得需要被服务的数据分散，可以减轻数据在排队系统中因等候而引起的传输时延。因此，候选中继的增加，会在一定程度上降低时延。

违约概率与积压的关系，以及数据到达率与积压的关系分别如图7和图8所示。

图7 违约概率与积压的关系

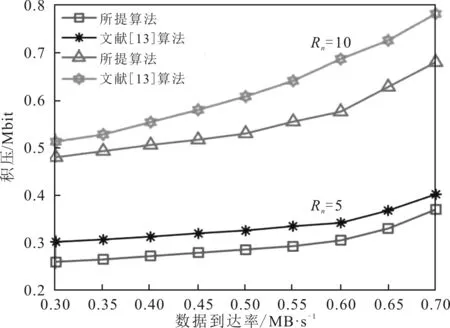
图8 数据到达率与积压的关系

由图7和图8所示，随着违约概率的增加，中继RSU对于具有突发特性的数据的处理能力会使得系统的积压减少。在允许一些数据不满足预定的性能指标的情况下，网络资源可以得到更充分的利用。同时，图8给出了不同数据到达率与积压上界的关系，可以看出，数据到达率的增大会增加系统的负载，中继RSU的积压也随之增大，候选中继数量的增加会分散需要被服务的数据，使得积压减少，并且相比于移动中的车辆节点，选择RSU作为中继，计算能力与存储空间会优于车辆节点，且RSU中留有充足的预信息，能够更加可靠地进行服务。因此，所提算法与文献[13]算法相比，能够得到更优的积压性能。

3 结语

在车联网中，由于车辆节点的运动特性带来的网络高度动态拓扑性和数据突发性等特点，如果选择移动中的车辆做为数据传输的中继节点，会导致链路连接不稳定，增大传输时延。在5G城市环境中，RSU达到全覆盖的场景下，选择RSU作为信息传输的中继能够在一定程度上减少链路连接的不稳定性以及降低由多跳传输所带来的时延。同时，采用SNC作为网络性能的分析工具进行路由的选择，更加符合车联网的特点。利用SNC建立SN的SAC与中继RSU的SSC，并分析竞争数据流存在时的SAC与SSC对时延与积压的关系。仿真结果表明，所提算法在选择中继RSU时，可以有效降低系统的传输时延与积压。