溯本求源 注重数学本质

张伟红

【摘要】中考数学命题以《数学课程标准》为依据，以“落实基础，注重过程，渗透思想，突出能力，强调应用，着重创新”为思想.中考题目大多源于课本的例題和习题，通过对教材习题的不断挖掘，一题多变，一题多解，逐渐变成了有价值的数学新问题，从而得到了一种解决此类问题的方法.

【关键词】  教材题目;初中数学;变式探究

纵观各地中考数学命题，其中很多题目都是源于课本的例题和习题，通过变式改编而成，这类题不仅较好地体现了命题的原则，还体现了基础性和学好课本知识的重要性，有着非常重要的导向作用，不仅能引导师生重视基础，重视教材，研究教材，用好用活教材，而且能激发学生学习数学的兴趣，挖掘习题的功能，促进学生对知识本质的理解.下面以一道教材的习题为例，突出解题的方法和题目的变式探究.

题目呈现 人教版八年级下册教材有这样一道题目：如，四边形ABCD是正方形，点E是边BC的中点.∠AEF=90°，且EF交正方形外角∠DCG的平分线CF于点F，求证：AE=EF.

学生看到本题会想到了一线三垂直模型，过点F作FH⊥BC，垂足为H，要证AE=EF，只需要证明Rt△ABE≌Rt△EHF，条件找到了两组角相等，即∠B=∠H=90°，∠BAE=∠HEF ，但是始终没有边相等.这两个三角形的确全等，但是边的条件找不到，此时引导学生换一种思路，要证AE=EF，能否构造一个与△ECF全等的三角形，请再思考.学生经过思考较容易的得到解法.如图2，取AB的中点H，连接EH，根据已知及正方形的性质利用ASA判定△AHE≌△ECF，从而得到AE=EF.

下面对本道习题做三种变式探究：

变式1 如果把“点E是边BC的中点”改为“点E是边BC上（除B、C外）的任意一点”，其他条件不变，那么结论“AE=EF”仍然成立吗，若成立，请写出证明过程;如果不正确，说明理由.

解法1 如图3，在AB上取一点M，使AM=CE，连接ME，

所以BM=BE，

所以∠BME=45°，∠AME=135°，

因为CF是正方形外交∠DCG的平分线，

所以∠DCF=45°，∠ECF=135°，

同（1）可证明△AME≌△ECF，

所以AE=EF;

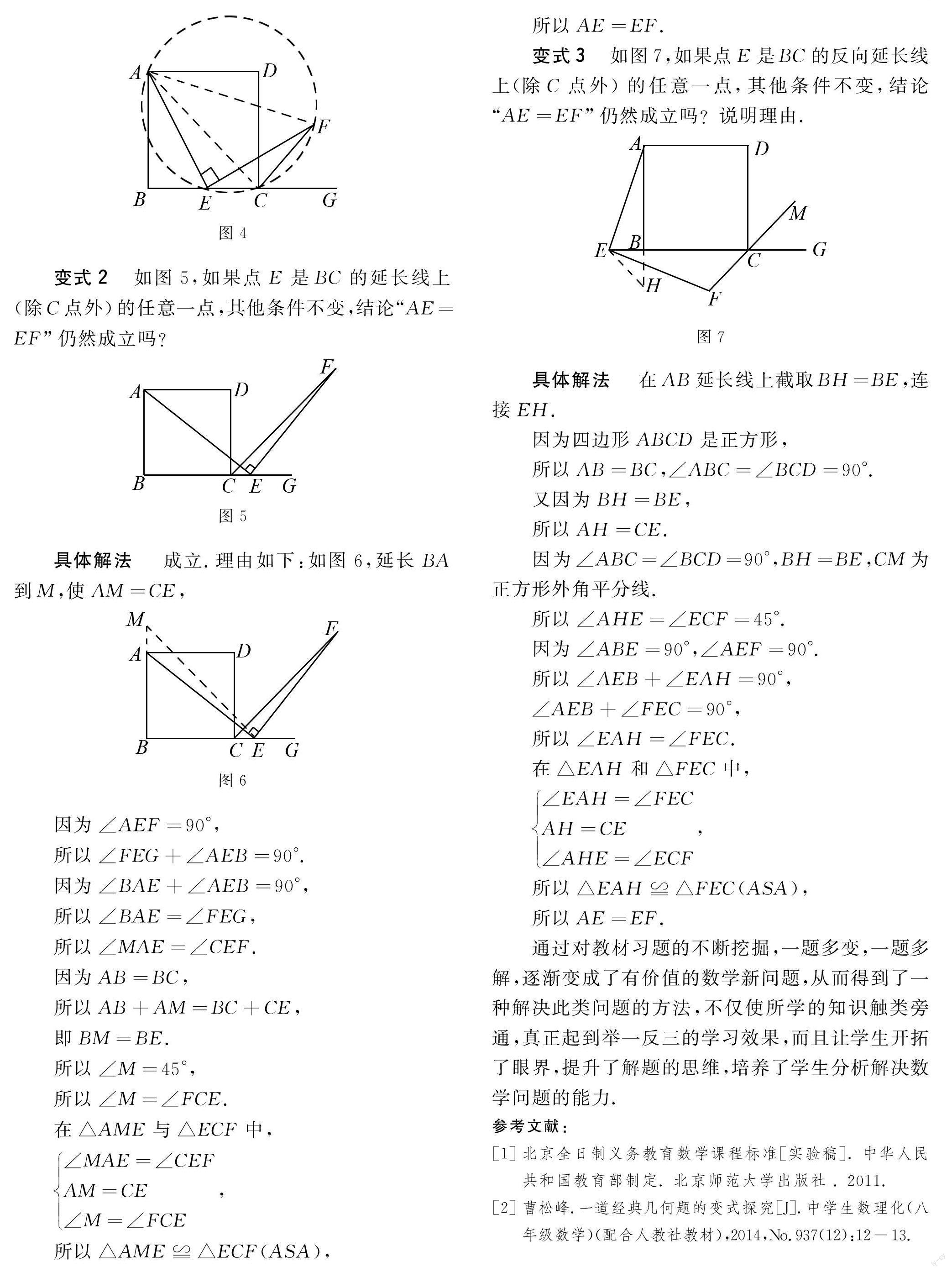
解法2 如图4，连接AC，易得到∠ACF=90°，又∠AEF=90°，所以点A、E、C、F在以AF为直径的同一个圆上，所以∠AFE=∠ACE=45°，从而∠EAF=45°，由∠AFE=∠EAF证明出AE=EF.

变式2 如图5，如果点E是BC的延长线上（除C点外）的任意一点，其他条件不变，结论“AE=EF”仍然成立吗？

具体解法 成立.理由如下：如图6，延长BA到M，使AM=CE，

因为∠AEF=90°，

所以∠FEG+∠AEB=90°.

因为∠BAE+∠AEB=90°，

所以∠BAE=∠FEG，

所以∠MAE=∠CEF.

因为AB=BC，

所以AB+AM=BC+CE，

即BM=BE.

所以∠M=45°，

所以∠M=∠FCE.

在△AME与△ECF中，

∠MAE=∠CEFAM=CE∠M=∠FCE，

所以△AME≌△ECF（ASA），

所以AE=EF.

变式3 如图7，如果点E是BC的反向延长线上（除C点外）的任意一点，其他条件不变，结论“AE=EF”仍然成立吗？说明理由.

具体解法 在AB延长线上截取BH=BE，连接EH.

因为四边形ABCD是正方形，

所以AB=BC，∠ABC=∠BCD=90°.

又因为BH=BE，

所以AH=CE.

因为∠ABC=∠BCD=90°，BH=BE，CM为正方形外角平分线.

所以∠AHE=∠ECF=45°.

因为∠ABE=90°，∠AEF=90°.

所以∠AEB+∠EAH=90°，

∠AEB+∠FEC=90°，

所以∠EAH=∠FEC.

在△EAH和△FEC中，

∠EAH=∠FECAH=CE∠AHE=∠ECF，

所以△EAH≌△FEC（ASA），

所以AE=EF.

通过对教材习题的不断挖掘，一题多变，一题多解，逐渐变成了有价值的数学新问题，从而得到了一种解决此类问题的方法，不仅使所学的知识触类旁通，真正起到举一反三的学习效果，而且让学生开拓了眼界，提升了解题的思维，培养了学生分析解决数学问题的能力.

参考文献：

[1]北京全日制义务教育数学课程标准[实验稿]. 中华人民共和国教育部制定. 北京师范大学出版社 . 2011.

[2]曹松峰.一道经典几何题的变式探究[J].中学生数理化（八年级数学）（配合人教社教材），2014，No.937（12）：12-13.