大型风力机异常功率数据清洗方法

李 琳,董 博,郑玉巧

(1.甘肃省特种设备检验检测研究院,甘肃 兰州 730050;2.兰州理工大学 机电工程学院,甘肃 兰州 730050)

风力机输出功率是表征其性能的关键指标[1].实测功率数据源于风力机的数据采集与监测系统(supervisory control and data acquisition,SCADA)，该系统记录的风功率数据存在大量集中、横向分布的异常数据簇和离群数据点[2]，严重影响功率数据的准确性.研究风力机功率数据清洗方法，形成高质量数据集尤为必要.

经验法结合3σ准则是目前相关研究中常采用的数据清洗方法[3]，但此类方法过于依赖经验，故风力机功率数据清洗工作亟待相关程序算法.基于统计原理的离散区间箱线图法[4-5]可有效处理异常离群数据点，即按风速等间隔划分数据区间并分区间使用箱线图剔除异常离群点.但该方法在横向分布的异常数据簇(通常由弃风限电导致)清洗方面明显失效，接近正常功率数据带的部分异常数据明显被误判为正常功率.另一研究思路是采用数据特征突变检测异常.以异常功率数据的突变统计特征为基础，最优组内方差算法((optimal interclass variance,OIV))[6]与其他几种方法[7-10]在离群数据点清洗方面取得较好效果.但横向分布异常数据方差特征多为渐变而非突变，此类方法亦失效.相关研究表明在横向分布异常功率数据清洗方面，聚类算法优势明显[11].基于密度的带噪声空间聚类算法(density-based spatial clustering of applications with noise，DBSCAN)的参与可有效提高风力机异常功率数据清洗质量[12]，然而该算法参数需要人工调整，不同风力机功率数据普适性难以保证.

鉴于此，本文提出基于DBSCAN聚类算法的改进清洗方法.该方法首先借助数据差分值粗估算法参数并获得初步聚类结果，继而通过数据簇统计特征相似性修正聚类结果.在2个数据集测试改进方法，并与离散区间箱线图法、OIV算法比较，证明本文所提方法清洗效果及其在不同数据集清洗的稳定性.

1 数据清洗方法

1.1 基于密度的带噪声空间聚类改进方法

DBSCAN算法[13]借助数据点邻域与邻域内最小包含点等概念计算数据点密度，但是该算法需经验法确定参数邻域Eps(最小包含点数Minpts = 4[13]).针对上述缺点进行改进.以0.5 m/s的风速间隔划分区间；设vin为切入风速；vout为切出风速；功率数据为U(j)={(xi，yi)|i=1,2,3,…,n}，U(j)为第j个区间功率数据集合，xi为第i个风速数据，yi为第i个风速下的功率数据，n为第j个风速区间内功率数据容量.改进说明如下：

1) 参数Eps的自适应估计.

在U(j)内依次计算数据点(xi，yi)与数据点(x1，y1)的欧式距离，即

(1)

将dist升序重排为dist′，计算dist′的一阶差分值，查询一阶差分值大于等于预设阈值d的第1个dist′值，并回溯查询对应的dist值，该数值为Eps估计值.其中，d为(0,0.7]内任意值.

(2)

式中：i为一阶差分值大于等于阈值d第1个dist值数据位置.

以d= 0.6为例，说明某型风力机风速在[8.5,9]内数据dist′一阶差分值，如图1所示.

可以看出，第1个不小于d的一阶差分值为点A(1 821,0.613 11)，回溯查询第1 821个功率数据的欧式距离为3.151 505，因此该区间内算法Eps= 3.151 505.

2) 聚类结果修正，即依据DBSCAN算法的聚类结果统计特征完成结果修正.

在[vin，vout]内，异常功率数据量远低于正常数据量[5].因此，由正常功率数据簇的3个指标(功率均值、功率标准差和风功率的spearman相关系数)构成的统计特征集{ms，ss，rs}必然与U(j)的特征集{mj，sj，rj}最为相似.通过计算上述2个集合的相似程度修正各类别的状态标记.经比较风力机实际运行记录，证明与该数据簇的欧式距离在(0,100]内的数据簇均为正常功率数据，其他为异常功率数据.仍以某型风力机风速在[8.5,9]内数据说明修正前后结果，如图2所示.

图2 修正前后算法聚类结果 Fig.2 The results of the method before and after modification

由图2a可以看出，DBSCAN算法可有效识别离群点，粗略识别多数正常数据并分离正常数据带周边数据簇.此时，计算各类别数据与正常数据，统计特征相似性,修正各类别数据实际标记，修正后聚类结果如图2b所示.改进方法整体计算流程如图3所示.

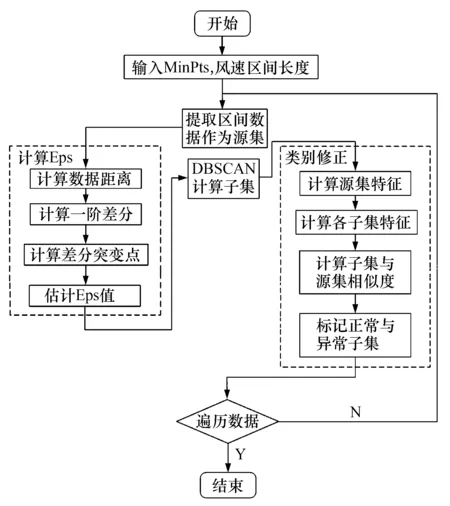
图3 改进方法计算流程图Fig.3 The improved method flow diagram

1.2 最优组内方差法

最优组内方差法(optimal interclass variance,OIV)的核心思路是设定初始方差阈值S后寻找对应的方差突变点，方差低于S的数据为正常数据，反之为异常.功率数据的方差突变位置λ为

(3)

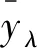
该算法清洗流程如下：

Step1 以0.5 m/s为间隔划分区间，提取功率数据；

Step2 按照功率数值升序重排每个区间的功率数据；

Step3 在每个区间内，根据式(1)依次计算前i个点的功率方差值(首个点的方差值恒为0)；

Step4 在每个区间内设定阈值S，功率方差小于S的为正常功率数据，大于等于S的为异常功率数据.

1.3 箱线图法

采用箱线图法对数据异常值进行清洗,剔除时需计算Q1分位数(x0.25)、Q2分位数(x0.5)、Q3分位数(x0.75)及数据上、下边缘(Lup、Ldown)5个特征值.通过数据上、下边缘确定正常数据范围，数据位置超出该范围的为异常数据.将数据按风速升序重排，上述3个分位数的计算公式为

(4)

式中：xp为数据的p分位数；n为区间内功率数据容量；[np]、[np]+1为计算出的p分位数的数据位置.

上、下边缘Lup与Ldown表达式为

(5)

式中：IQp为Q1分位数(x0.25)与Q3分位数(x0.75)的间隔.

该算法清洗流程如下：

Step1 以0.5 m/s为间隔划分区间，提取功率数据；

Step2 按照功率数值升序重排每个区间的功率数据；

Step3 在每个区间内，根据式(4)和式(5)计算数据上、下边缘特征值；

Step4 在每个区间内判断数据状态，数据位置处于(Ldown,Lup)的为正常功率数据，否则为异常功率数据.

1.4 清洗质量评价指标

功率数据清洗质量采用正常数据的准确率、召回率及前2个指标的调和平均数F1定量评价[14].

正常功率数据的准确率P表达式为

(6)

召回率R表达式为

(7)

F1度量表达式为

(8)

式中：正常功率数据为正例，异常功率数据为反例；TP是算法判断为正常功率中识别正确的功率数据(真正例)；FP是算法判断为正常功率中识别错误的功率数据(假正例)；FN是算法判断为异常功率中识别错误的功率数据(假反例).

2 实例分析

选用江西某风场2.5 MW风力机SCADA系统从2018年7月至2019年7月的实测功率数据.该型风力机切入风速vin=3 m/s，额定风速vrated=10 m/s，切出风速vout=25 m/s，数据采样间隔为10 min.选用2台该型风力机实测功率数据，通过人工逐点辨认法区分正常与异常功率数据并标记.其中1台风力机的实测功率数据作为实测数据集，另1台风力机的实测功率数据用于构建合成数据集.

采用蒙特卡洛方法为合成数据集引入异常功率数据[14].引入异常数据分为离散异常功率和限电异常功率.2类异常功率数据在风速轴均服从Weibull分布(与正常数据同分布)，离散异常功率数据在功率轴服从均匀分布，限电异常功率数据在功率轴服从正态分布.

数据集详细信息如表1所列.

表1 合成数据集与实测数据集信息Tab.1 Details of composite and measured data

2.1 合成数据验证

分别采用OIV算法、箱线图法及本文所提改进方法对合成数据集进行清洗.

OIV算法的方差突变点λ通过式(3)计算，该算法对风力机异常功率数据清洗结果如图4所示.

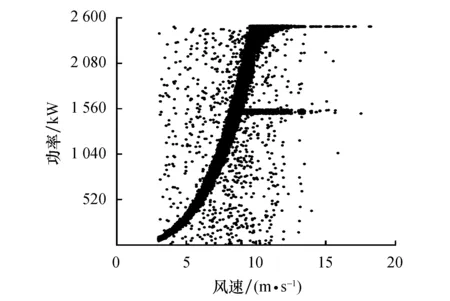
图4 OIV算法清洗异常功率数据结果 Fig.4 The cleaning result of the composite data with the OIV

可以看出，风速在(2.5,20)内，经该算法清洗后的正常功率数据周围散布着明显的离散分布异常功率数据，且横向分布异常功率数据基本未能去除，因此OIV算法的异常功率数据清洗效果较差.

为定量评价清洗效果，通过式(6～8)计算得到OIV算法的P值为95.62%，R值为76.02%，F1值为84.70%.上述指标表明，经OIV算法清洗后保留的数据包含4.38%的异常功率数据，正常功率数据占比为95.62%，且该部分数据占全部正常功率数据的76.02%.因此，在特定的数据集中OIV算法清洗异常功率数据工作是失效的.

箱线图法对风力机异常功率数据清洗结果如图5所示，上、下边缘Lup和Ldown通过式(4)和式(5)计算得到.

可以看出：风速在(2.5,20)内，离散分布异常功率数据基本去除；在正常功率数据带边缘仍存在部分数据簇呈锯齿状，该现象为异常功率数据未能有效清洗所导致；部分横向分布异常功率数据未能清洗;风速在(0,3)内，离散分布异常功率数据未能去除.由于本文使用数据集不包含停机、启动数据，所以风速小于3 m/s时不存在正常运行数据.因此，当正常功率数据的样本容量低于异常数据时，箱线图法存在失效可能.

计算评价指标得到箱线图法的P值为99.13%，R值为99.02%，F1值为99.07%.箱线图法的F1值比OIV算法(84.70%)高出14.37%，表明箱线图法在风力机功率数据清洗工作方面优于OIV算法.同时,P值与R值的计算结果表明,经箱线图法清洗后保留的数据包含0.87%的异常功率数据，正常功率数据占比为99.13%，且该部分数据占全部正常功率数据的99.02%.由此可见，箱线图法可较好地清洗异常功率数据，且清洗效果优于OIV算法.

本文所提改进方法对风力机异常功率数据清洗结果如图6所示，Minpts值为4[14]，Eps值通过式(1)和式(2)分区间自适应计算.

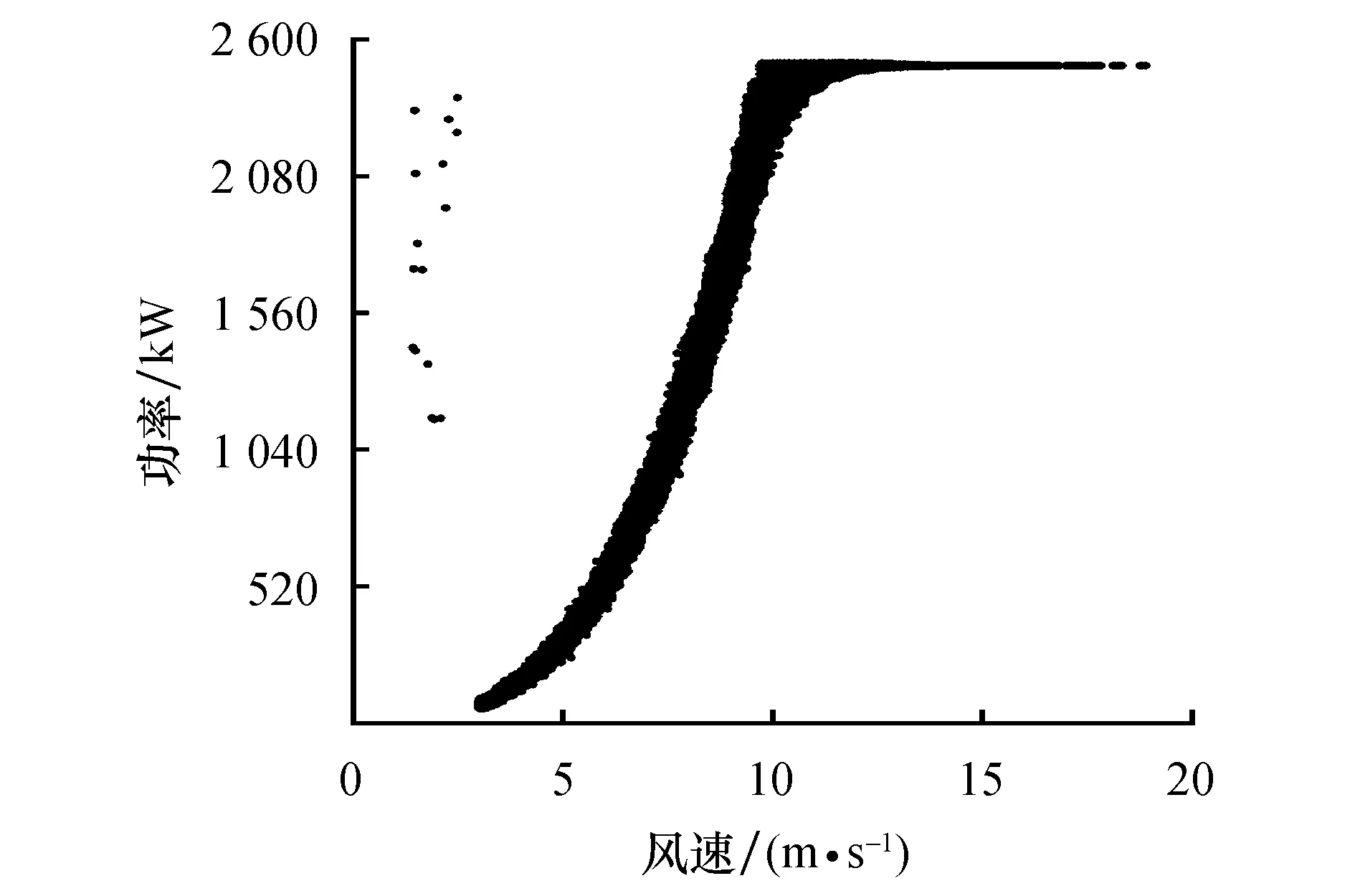
图6 改进方法清洗异常功率数据结果Fig.6 The cleaning result of the composite data with the improved metho

可以看出：风速在(2.5,20)内，离散分布异常功率数据基本去除；横向分布异常功率数据完全去除；风速在(0,3)区间内，离散分布异常功率数据未能正确去除.

进一步计算评价指标得到改进方法的P值为99.70%，R值为99.78%，F1值为99.74%.改进方法的F1值比OIV算法(84.70%)高出15.04%，比箱线图法(99.70%)高出0.04%，表明改进方法在风力机功率数据清洗工作方面优于OIV算法和箱线图法.同时,P值与R值的计算结果表明,经改进方法清洗后保留的数据包含0.30%的异常功率数据，正常功率数据占比为99.70%，且该部分数据占全部正常功率数据的99.78%.由此可见，改进方法可较好地清洗异常功率数据，且清洗效果优于OIV算法与箱线图法.

2.2 实测数据验证

为验证改进方法清洗不同数据集时的稳定性，在实际运行数据中验证改进方法的有效性十分必要.分别采用3种方法清洗该数据集，在清洗过程中，OIV算法的方差突变位置λ通过式(3)计算，其清洗异常功率数据结果如图7所示.

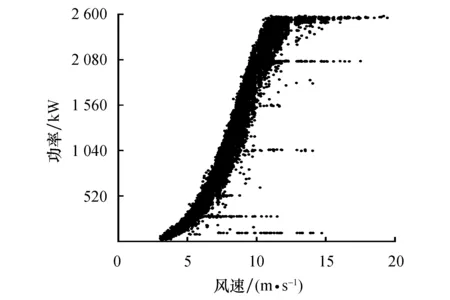
图7 OIV清洗异常功率数据结果 Fig.7 The cleaning result of the measured data with the OIV

可以看出，OIV算法保留的功率数据中存在大量离散、横向分布异常功率数据，且均位于正常功率数据带以下，同时在风速12.5 m/s附近正常功率数据被误删.因此OIV算法在实测数据集的清洗效果较差.

计算清洗效果定量评价指标得到OIV算法的P值为70.01%，R值为57.77%，F1值为63.30%.由P值与R值可知,经OIV算法清洗的数据包含29.99%的异常功率数据，正常功率数据占比为70.01%，且该部分数据占全部正常功率数据的57.77%，OIV算法的F1值相较于合成数据集(84.70%)下降了21.40%.由此可见，OIV算法在处理实测数据集时清洗质量较低，且在清洗不同数据集时稳定性较差.

箱线图法清洗异常功率数据结果如图8所示，上、下边缘Lup和Ldown通过式(4)和式(5)计算得到.

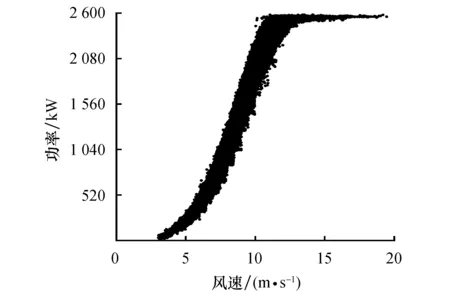
图8 箱线图法清洗异常功率数据结果Fig.8 The cleaning result of the measured data with the box-plots based method

可以看出：离散分布异常功率数据基本去除，但在风速10 m/s附近存在位于正常数据带顶部的异常功率数据未能清洗；正常功率数据带边缘呈明显锯齿状；部分横向分布异常功率数据未能清洗.

计算评价指标得到箱线图法的P值为95.94%，R值为97.69%，F1值为96.81%.由P值与R值可知，经箱线图法清洗的数据包含4.06%的异常功率数据，正常功率数据占比为95.94%，且该部分数据占全部正常功率数据的97.69%，箱线图法可有效清洗实测数据集.箱线图法的F1值相较于合成数据集(99.07%)下降了2.26%，表明箱线图法清洗不同数据集时稳定性较好.同时,该方法的F1值比OIV算法(63.30%)高出33.51%.因此，清洗实测数据集时，箱线图法仍优于OIV算法.

改进方法对实测数据集的清洗结果如图9所示，Minpts值为4[13]，Eps值通过式(1)和式(2)计算.

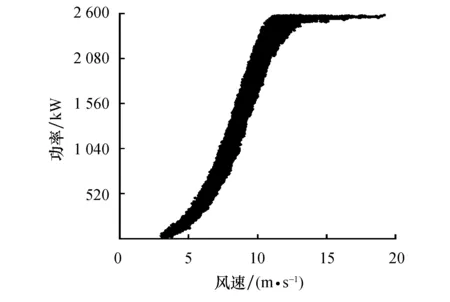
图9 改进方法清洗异常功率数据结果Fig.9 The cleaning result of the measured data with the improved method

可以看出，离散、横向分布异常数据均被去除，改进方法对实测数据集的清洗效果较好.计算定量评价指标得到改进方法的P值为97.97%，R值为97.73%，F1值为97.85%.由P值与R值可知，经改进方法清洗的数据包含2.03%的异常功率数据，正常功率数据占比为97.97%，且该部分数据占全部正常功率数据的97.73%，改进方法可有效清洗实测数据集.改进方法的F1值比OIV算法(63.30%)高出34.55%，比箱线图法(96.81%)高出1.04%，表明在清洗实测数据集中，改进方法仍优于OIV算法和箱线图法;同时,相较于合成数据集(99.74%)，改进方法的F1值下降了1.89%，低于OIV算法(21.40%)与箱线图法(2.26%).因此，改进方法清洗不同数据集时稳定性比OIV算法和箱线图法更优.

3 结论

通过2个数据集分别验证3种方法的清洗效果.改进方法F1值最低为97.85%，高于OIV算法(63.30%)与箱线图法(96.81%)，表明改进方法可有效清洗风力机异常功率数据，且清洗质量最优.清洗不同风力机数据时，改进方法的F1值下降了1.89%，低于OIV算法(21.40%)与箱线图法(2.26%)，表明相较于OIV算法与箱线图法，改进方法清洗不同数据集时更稳定.