改进的D-t-SNE滚动轴承故障数据集降维方法
赵荣珍,薛 勇,吴耀春
(兰州理工大学 机电工程学院,甘肃 兰州 730050)
随着人工智能技术和工业互联网的快速发展,工业智能化已成为当前流程工业装备制造业发展的重要趋势.同时,随着工业智能化程度的不断提高,机械设备在运行过程中的状态监测数据量与日俱增,促使关于旋转机械的智能故障诊断技术必须加快步入工业大数据的新时代[1-3].由此带来的关键性问题之一是如何从价值密度较低的海量高维信息资源中挖掘出有价值的故障状态信息,这已成为当前基于数据驱动的智能旋转机械故障诊断领域的前沿热点问题.滚动轴承是旋转机械中最常用的部件之一,其轻微缺陷就可能导致整个机械系统发生故障.因此,对滚动轴承开展智能决策技术的故障降维与分类问题研究具有重要的科学研究意义与工程应用参考价值.
然而在对滚动轴承进行故障诊断时,为了尽可能更加全面地描述出典型故障的状态,通常需要从时域、频域以及时频域等多角度提取出能够全方位描述故障状态的量化故障特征.由此产生的问题是故障特征中通常包含着大量的相关信息和冗余特征.很显然,这些不利因素将会导致人工智能自动辨识结果的准确性降低[4-6].因此,探究消除相关信息和冗余特征、降低高维故障数据集维数的有效方法,对于挖掘出能够反映旋转机械运行状态的有价值故障状态信息,从而降低故障分类的难度,提高故障的辨识准确率尤为重要.
流形学习自提出以来,在故障诊断领域引起了广泛的关注.流行学习的原理是假设所有数据都位于某光滑流形上,然后将高维数据在流形中的几何结构特征保留至低维特征中[5-6].经典的非线性流形学习算法,如等距映射(isometric mapping,ISOMAP)[7]、随机近邻嵌入(stochastic neighbor embedding,SNE)[8]和t分布随机近邻嵌入(t-distributed stochastic neighbor embedding,t-SNE)[9]等,都能够有效地处理高维非线性数据.其中,t-SNE算法是Ven der Maaten等学者于2008年在SNE算法基础上提出并改进的新型流形学习降维算法,具有较好的降维和可视化效果[9-10].目前,基于t-SNE算法的滚动轴承故障诊断方法层出不穷.于重重等[11]将t-SNE算法与时间卷积网络相融合,提出了新的轴承状态检测方法,该方法计算t-SNE算法降维后得到的特征子集样本熵,以样本熵为特征,将其输入时间卷积网络中预测轴承的退化趋势.姜战伟等[12]提出了多尺度时不可逆振动信号复杂度测量方法,用来计算轴承复杂信号的故障特征,利用t-SNE算法对新的故障特征进行降维,并通过粒子群优化支持向量机对低维故障特征进行故障模式辨识,从而实现故障诊断.
但是在t-SNE算法的降维过程中,随着待处理数据集维数的持续升高,欧氏距离会降低数据样本点之间距离的可区分度.由此导致的不利后果是数据点到其近邻点与远邻点之间的距离近似相等,难以通过距离对数据点进行有效区分.而测地距离指标(geodesic distance,GD)则能够利用邻域图中的最短路径长度来逼近数据点之间的真实距离,从而提供比欧氏距离更大的距离区分度[13-14].
基于上述分析,本研究拟对测地距离与t-SNE算法相结合的滚动轴承故障数据集降维方法进行探讨.欲为更好地保持原始高维故障数据集局部与全局几何结构特征,降低滚动轴承故障数据集的分类难度,提供理论参考依据.
1 相关算法简介
1.1 测地距离指标
该指标是指利用最短路径(Dijkstra)算法,通过数据近邻点之间的局部邻域距离对真实距离进行估计的距离度量公式,示意图如图1所示.假设数据点位于某流形上,点A、C为该流形上的任意两点,则它们之间的欧氏距离可表示为直线段AC,测地距离可表示为绕流形表面的曲线段ABC.由图1可以看出,在高维空间中,测地距离比欧式距离能够更好地描述数据点之间的真实距离,增大数据点之间距离的可区分度,从而更好地描述数据的几何结构特征.
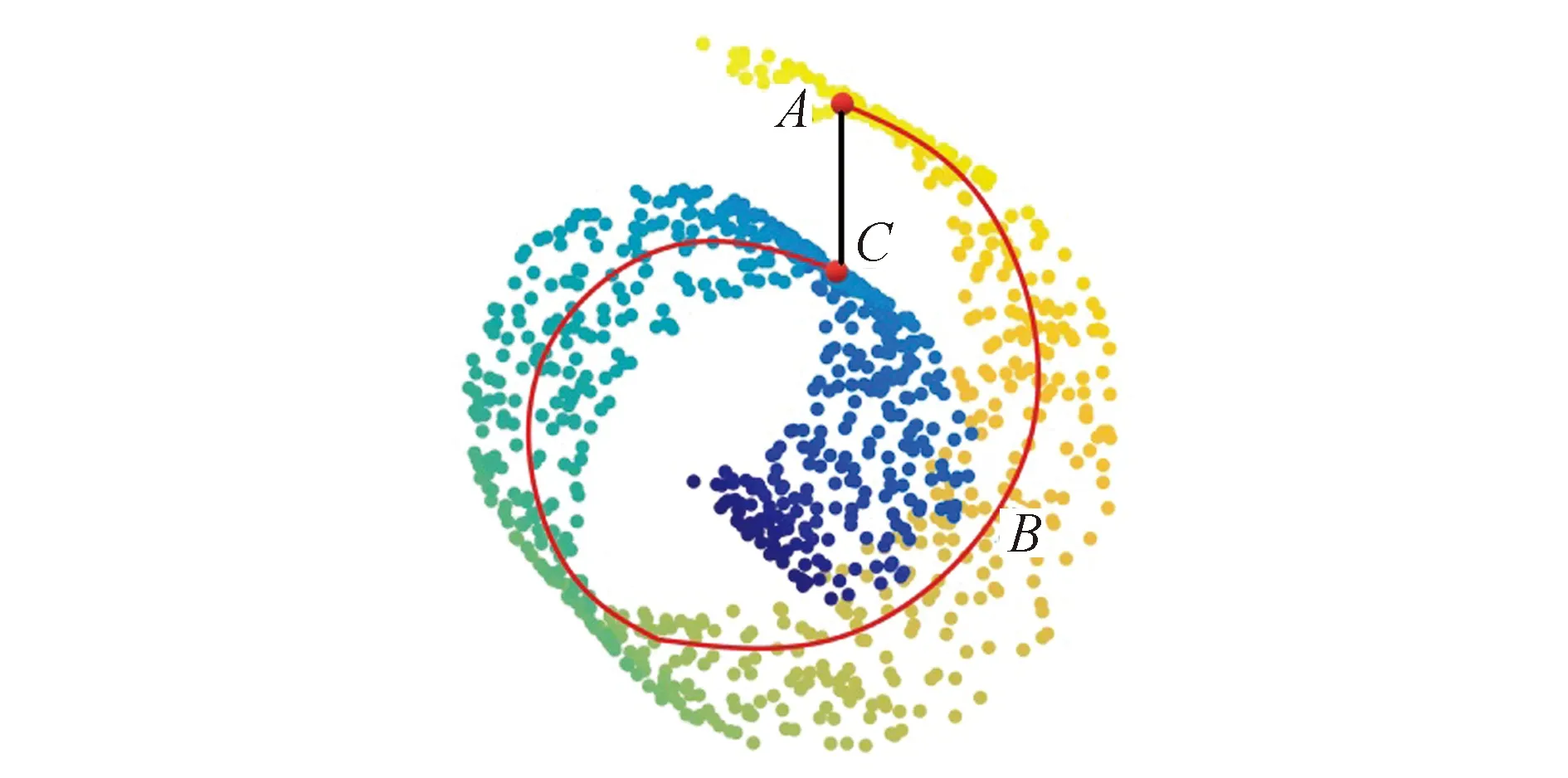
图1 测地距离示意图Fig.1 Schematic diagram of geodesic distance
Dijkstra[14]是经典的单源最短路径算法,用于求解从起点开始到其他所有节点的最短路径.它的基本思路是从起点开始逐层向外扩展,直到扩展至所有点为止.该算法寻找最短路径的方式为:将带权图中的所有节点存入集合S、T中,两集合中分别存放的是已确定为最短路径的节点和未确定为最短路径的节点,需按照最短路径长度递增的顺序逐个把T中的节点选入S中,直到S中包含所有节点为止.该算法的主要步骤如下:
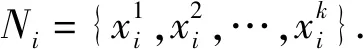
(1)
在图G中利用最短路径算法计算任意两点间的最短路径,其距离寻优经过的路径记为PG[14],即
pG(xi,xj)={xi,xi+1,…,xj-1,xj}
(2)
则数据点i、j之间的测地距离可表示为
(3)
1.2 t-SNE算法原理
该算法作为流形学习算法通常被用于非线性数据的降维过程中,其高维数据的可视化效果较好.它的核心思想是:假设高维数据和低维数据分别服从高斯分布和t分布,则通过欧氏距离构造高维数据的概率分布,通过t分布构造低维数据的概率分布;利用损失函数使得高维概率分布与低维概率分布尽可能相似,从而得到降维结果.步骤如下[9]:
(1) 假设高维输入样本为X={x1,x2,…,xi,…,xn|xi∈RD},高维空间的概率分布定义为pj|i,表示xj可能成为xi近邻点的概率,即
(4)
式中:pi|i=0;pj|i≠pi|j;γi为中心点是xi的高斯方差,可通过二分法搜索指定的复杂度prep得到,复杂度的定义为prep(Pi)=2H(Pi),H(Pi)为香农信息熵,表达式为
(5)
(2) 高维空间中具有对称性的联合概率分布为
(6)
其中,对任意的i、j都有pij=pji.
(3) 设Y={y1,y2,…,yn}为高维数据集的低维初始嵌入坐标,则低维服从t分布的联合概率分布为
(7)
(4) 构建损失函数KL(Kullback-Leibler)散度,它是用来测量高维与低维概率分布之间差异性大小的.其值越小,说明高维和低维之间的概率分布越相似;其值越大,说明高维和低维之间的概率分布差异性越大.即
(8)
(5) 为了获得低维特征,通过梯度下降法最小化KL散度,即
(9)
对其进行迭代更新,即
(10)
式中:ξ代表学习率;η(t)代表第t次迭代系数.
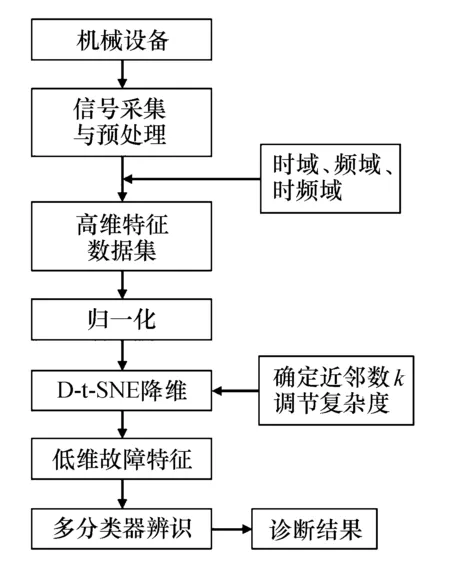
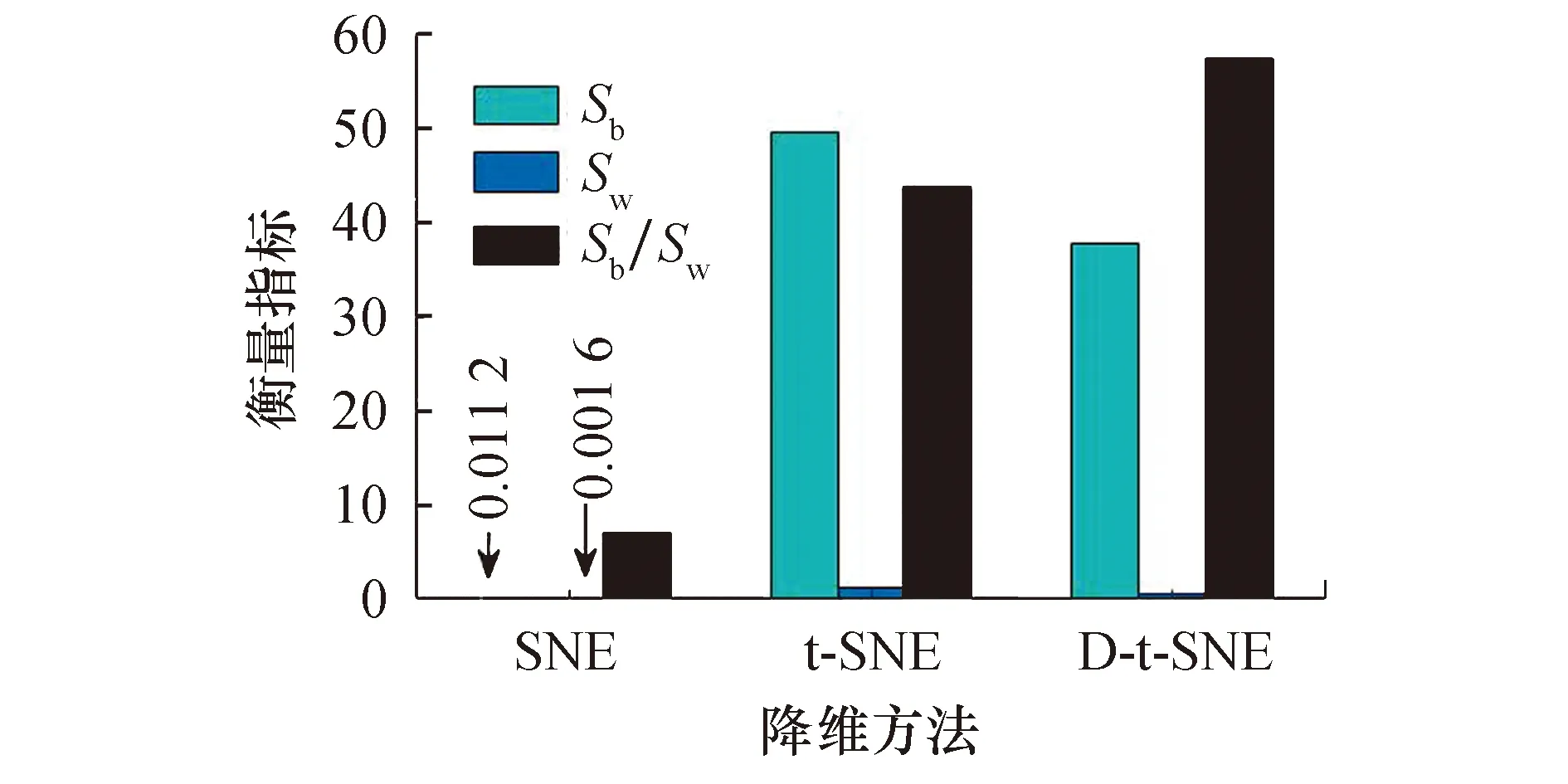
(6) 重复式(7~10),可得到低维映射结果Y={y1,y2,…,yi,…,yn|yi∈Rm,m 上述t-SNE算法的目的是保持降维前、后数据集的局部与全局几何结构特征基本一致,但该算法保持后者基本一致的能力较弱[10,15].此外,该算法还会出现在高维空间中距离较远的两数据点之间计算距离反而变小,近邻点与远邻点之间的可区分度降低.这将导致经降维运算得到的低维数据集仍然存在着不利于实施分类运算的数据拥挤问题. 鉴于t-SNE算法是通过低维概率分布模拟高维概率分布从而实现降维的,那么高维故障数据集的几何结构特征保留得越完整,则后续的降维效果以及故障分类准确率也就越高.从对t-SNE算法的介绍可知,随着待处理数据集维数的升高,该算法会导致近邻点与远邻点之间的距离区分度逐渐降低,无法有效保持降维前、后数据集的局部与全局几何结构特征基本一致,而且该算法对全局几何结构特征的保持能力较弱.从对测地距离的介绍可知,该方法能够通过计算最短路径的方法近似求得数据点间的真实距离,增大数据点之间的距离区分度,有效地保持高维数据的局部与全局几何结构特征.因此,将2种方法的优点进行结合.本研究拟设计新的流形学习降维算法,即通过测地距离改进t-SNE算法的D-t-SNE(dijkstra-t-distributed stochastic neighbor embedding)故障数据集降维方法,并将其用于滚动轴承高维故障数据集降维处理中.算法的原理描述如下: 输入 高维故障数据集X={x1,x2,…,xi,…,xn|xi∈RD; 输出 低维特征子集Y. Step1 输入高维故障数据集,构建邻域图G,根据式(3)计算其测地距离. Step2 根据式(6)和式(7)分别构建高维联合概率分布和低维联合概率分布,设定复杂度大小. Step3 根据式(8)建立损失函数,通过梯度下降法对其求解. Step4 利用式(10)进行更新迭代,获得低维特征子集Y. D-t-SNE算法的主要思路包括:首先,构建能够全面描述故障状态的多域高维故障数据集,通过k近邻法构建出能够正确表达数据几何结构特性的邻域图,在邻域图中利用最短路径算法近似求得与真实距离较为接近的测地距离;随后,用测地距离替代欧氏距离计算高维故障特征数据集的联合概率分布,再通过t分布建立低维联合概率分布;最后,通过最小化高维和低维概率分布之间的损失函数E,获得最佳的低维特征. 该算法中所提出的复杂度属于变参数[16],它的作用是调节算法降维过程中保持全局信息与局部信息的比例.值越小,算法更倾向于保留局部信息;值越大,算法更倾向于保留全局信息.按经验复杂度通常取5~50. 由式(11~13)可知,Sb越大,Sw越小,γ也就越大,表明低维敏感数据集的聚类与分类效果越好. 故障诊断的目标是在实现故障分类的基础上实现故障的自动辨识,故通过KNN[18](k-nearest neighbor)、支持向量机[19](support vector machine,SVM)和BP[20](back propagation)这3种分类器来验证低维敏感特征子集的分类准确率.分类准确率越高,表明相应算法的降维效果越好,辨识准确率越高. 本研究所提方法的故障诊断流程图如图2所示,它的具体应用步骤如下: 图2 D-t-SNE的故障诊断流程图Fig.2 The fault diagnosis flow chart of the D-t-SNE Step1 采集机械设备的振动信号,消噪后计算多域的量化故障特征,构建高维故障数据集. Step2 对高维故障数据集进行归一化处理. Step3 计算测地距离GD,设置近邻数k=12. Step4 计算高维空间联合概率分布pij和低维空间联合概率分布qij,复杂度prep设为50,通过最小化KL散度求得降维结果. Step5 将特征子集分为训练集和测试集,利用多种分类器分别验证测试集的模式辨识效果,确定测试集的故障类别. 在本研究中,滚动轴承故障模拟实验是在如图3所示的厚德仪表HZXT-DS-001型转子实验台上进行的.所选故障轴承是型号为6308的深沟球轴承,模拟了如图4所示的滚动体破裂、保持架破裂、内圈裂纹、外圈裂纹和正常共5种状态故障.为能够全面地进行分析,分别用1个加速度传感器和2个电涡流传感器采集故障轴承的振动响应,每次采集1种故障轴承.设置采样频率为8 000 Hz.在转速为3 000 r/min时采集5种故障状态各80组样本供本研究使用.将每种故障数据以40∶40的比例分为训练集和测试集,5种状态下的训练集和测试集均为200组样本.为能够从多视角相对比较全面地描述出故障轴承不同故障状态之间的差异性,最终确定使用如表1所列的时域、频域和时频域共32个特征描述单个通道信号的特征,用5个通道信号的特征构建出能够描述滚动轴承运行状态的高维原始故障数据集,共由32×5=160个特征组成. 图3 双跨转子实验台Fig.3 Double span rotor test bench 图4 故障轴承Fig.4 Fault bearings diagram 表1 故障特征参数Tab.1 Fault characteristic parameters 为验证D-t-SNE算法的有效性,本研究选择了t-SNE和SNE算法进行降维性能对比.在使用期间,上述3种算法的复杂度均设为prep=50;D-t-SNE算法的近邻数设为k=12.最终经SNE、t-SNE和D-t-SNE这3种算法降维后得到的低维特征子集可视化效果如图5所示.其中,图5a是原始高维故障数据集的分布状况,图5b~5d分别是经SNE、t-SNE和D-t-SNE算法降维后得到的低维特征子集可视化效果. 由图5d可以看出,使用D-t-SNE算法降维后的可视化效果明显优于其他2种算法,此时轴承的5种状态可以有效地被分离开.很显然,此结果呈现的特点是类内距离较小,类间距离较大,不同类之间无混叠现象.由图5c可以看出,经t-SNE算法降维后,滚动体破裂与内圈裂纹的类间距离较小,外圈裂纹与正常状态之间产生了一定的混叠现象,各故障状态之间无法完全有效地被分离开.由图5b可以看出,经SNE算法降维后得到的结果最差,类间较为聚集,类内较为分散,各状态之间均存在着较为严重的混叠现象,类间因拥挤严重呈现出难以实施分类的状况. 图5 各算法的降维效果Fig.5 Dimensionality reduction effect of each algorithm 为衡量各方法的降维效果,在研究中使用衡量指标Sb、Sw以及可分性指标γ=Sb/Sw对3种算法的降维效果进行评价,结果如图6所示,各算法的3项指标分别按照从左至右的顺序进行排列. 图6 各方法降维后测试样本的评价结果Fig.6 Evaluation results of test samples after dimensionality reduction by each method 因故障诊断的目标是模式辨识,故为了进一步衡量各算法的降维效果,还利用KNN、SVM和BP这3种分类器分别验证经各算法降维后测试样本的分类准确率,结果如表2所列.此时,设置KNN的k=12;SVM采用高斯径向基核函数,通过网格搜索法[21]对其核参数和惩罚因子进行寻优;BP分类器的隐含层神经元个数设为10. 表2 各方法的分类准确率Tab.2 The classification accuracy of each method 由图6和表2对比分析可以看出:1) 经SNE算法降维得到的低维特征子集降维效果与分类准确率最差,原因是非对称的条件概率导致算法效果较差,同时高斯分布使得该算法对离群点较为敏感,从而产生拥挤问题;2) 经t-SNE算法降维得到的低维特征子集降维效果与分类准确率较差,原因是欧式距离会降低高维数据点间距离的可区分度,导致数据点间的距离不易区分,在一定程度上影响算法的降维效果与分类准确率;3) 而经D-t-SNE算法降维得到的低维特征子集降维效果与分类准确率最好,原因是该方法能够利用测地距离有效地逼近了高维空间中数据点间的真实距离,增大了距离的可区分度,有效地提高了低维概率分布对高维概率分布模拟的准确性,从而优化降维效果,提高故障的分类精度.上述分析充分表明,本研究提出的D-t-SNE算法在用于滚动轴承故障诊断时,具有更好的降维效果与故障分类准确率. 1) 为验证D-t-SNE算法在小样本情况下是否具有稳定性,本研究以改变训练样本与测试样本比例的方式,通过KNN、SVM和BP分类器分别验证了不同比例下各算法降维后测试样本的分类准确率.训练样本与测试样本的比例分别设为10∶70、20∶60、30∶50、40∶40、50∶30、60∶20、70∶10,得到的识别效果如图7所示.由图7可以看出:随着训练样本的增多,所获得的有价值故障状态信息也就越多,因此,各方法的平均识别率整体呈上升趋势;而随着训练样本的减少,SNE和t-SNE算法降维后得到的低维特征子集识别率下降比较明显,此时D-t-SNE算法仍然能够保持较高的平均识别率,且在任意分类器中的识别效果均优于其他2种算法.这说明,D-t-SNE算法具有更高的稳定性和更强的信息挖掘能力. 图7 变训练样本对应的平均识别率Fig.7 The average recognition rate corresponding to the variable training sample 2) 为验证D-t-SNE算法的抗噪性能,本研究参考文献[22]的评价方法,设置每种故障状态的训练和测试样本均为40组,分别设置系数α=0、0.5、1、1.5、2的随机噪声对测试样本进行扰动,之后再利用KNN、SVM和BP这3种分类器分别验证3种算法在不同干扰情况下的分类准确率,结果如图8所示.由图8可以看出,随着噪声干扰程度的增加,3种算法的平均识别率均有所下降,但D-t-SNE算法在不同的噪声干扰下均能够保持较高的平均识别率,且在任意分类器中的识别率准、确率均最高.由此说明,D-t-SNE算法具有相对比较高的抗噪性能,即鲁棒性较强,更适应复杂的动态工作环境. 图8 不同噪声干扰下各算法的平均识别率Fig.8 The average recognition rate of each algorithm under different noise interference 3) 因旋转机械在工作状态下转速具有一定的波动性,故通过变工况实验验证D-t-SNE算法对速度波动的适应性.实验选择用2 600、2 800、3 000 r/min这3种不同转速的混合数据模拟变工况环境下的速度波动情况.分别在3种不同转速的每类故障中选取20组数据(共60组)混合后作为训练样本,另取各转速下每类故障中不重复的20组数据(共60组)混合后作为测试样本.通过KNN、SVM、BP这3种分类器验证变工况条件下经各算法降维后测试样本的故障辨识效果,结果如表3所列.由表3可以看出,在变工况条件影响下,3种算法降维后得到的测试样本平均识别率均有所下降,但SNE和t-SNE算法的识别率下降较为明显,识别效果较差,而D-t-SNE算法的识别率下降幅度较小,识别效果明显优于其他2种算法.由此说明,D-t-SNE算法可以在复杂工况条件下获得较高的识别率,适应性较强. 表3 变工况条件下各算法的平均识别率Tab.3 Average recognition rate of each algorithm under variable working conditions 4) 通过降维过程所需时间对算法的耗时性能进行分析.实验电脑的配置为Intel Corei7-8750H、2.20GHz CPU、RAM 8GB、Windows10 64位操作系统,安装的软件为MATLAB R2018b.3种算法降维过程所需时间如表4所列.由表4可以看出,D-t-SNE算法降维过程所需时间相比t-SNE和SNE算法有微弱的增加.然而,相对其降维效果与模式辨识准确率的巨大提升,所需时间在同一数量级的增加在可接受范围内,因此满足要求. 表4 各算法降维所需时间Tab.4 The time required of each algorithm to reduce dimension 1) 本研究以t-SNE算法为基础,通过引入测地距离指标,建立了新的D-t-SNE故障数据集降维算法.该算法能够通过测地距离近似计算数据点间的真实距离,增大数据点间距离的区分度,可有效地保持高维数据的局部与全局几何结构特征. 2) 相比其他算法,本研究提出的D-t-SNE算法具有更好的降维效果与更高的故障辨识精度,可为旋转机械非线性高维故障数据集更好地保留其局部与全局几何结构特征的降维和可视化工作提供全新的解决方案.下一步值得注意的应该是考虑如何自适应选择算法复杂度的问题.2 D-t-SNE降维算法
2.1 建立的D-t-SNE算法
2.2 参数对算法降维效果的影响分析
2.3 降维效果衡量指标

2.4 基于D-t-SNE算法的故障诊断模型
3 实验验证
3.1 实验数据说明



3.2 降维结果的可视化情况

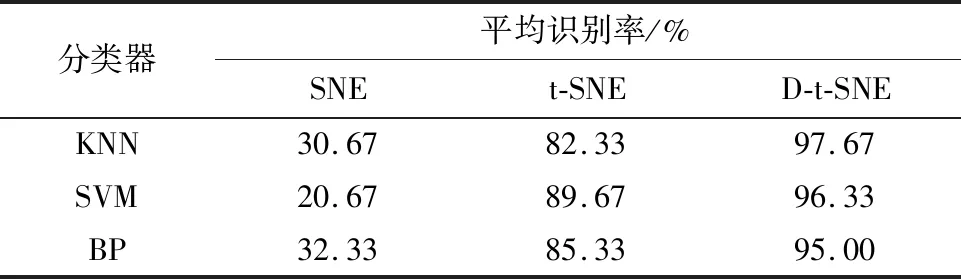
3.3 降维效果的衡量

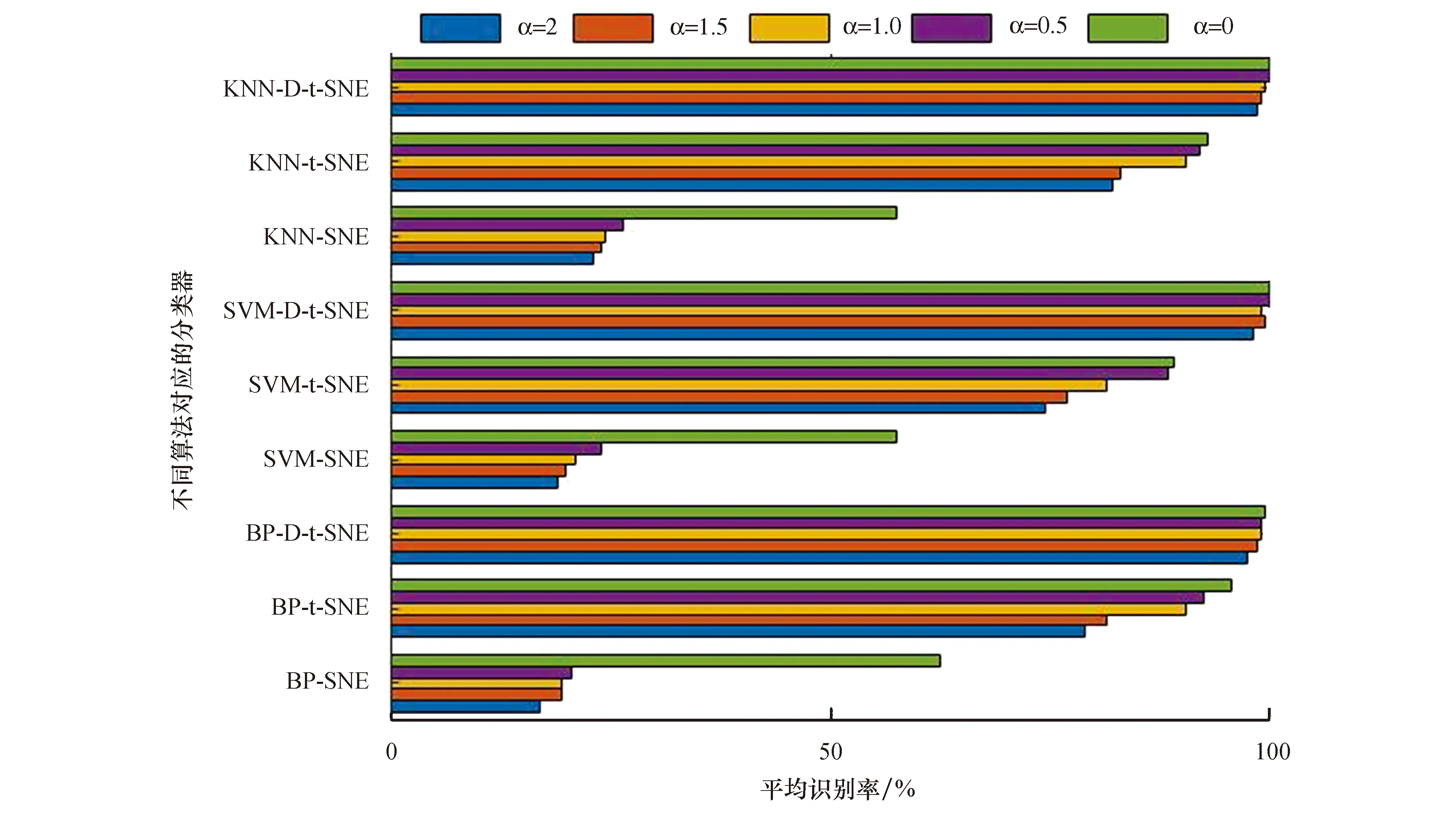
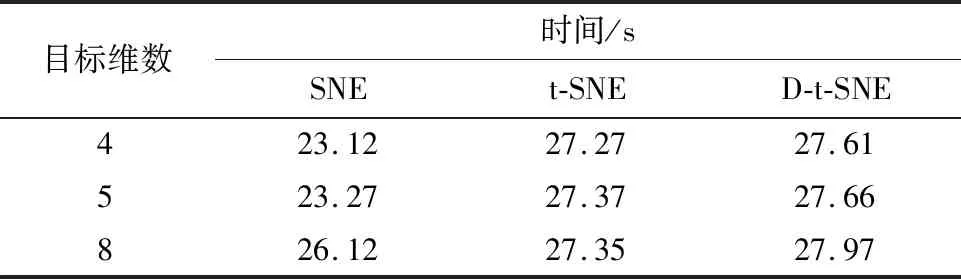
3.4 算法的性能评价情况

4 结论

