基于优化最小二乘支持向量机的数控机床热误差建模分析

李有堂,汤雷武,黄 华,吴荣荣

(兰州理工大学 机电工程学院,甘肃 兰州 730050)

机床热误差是由机床的不同构件热效应耦合作用产生的,最高占综合误差的70%[1-2].因此,解决热误差问题是提高机床加工精度的首要任务.

误差补偿法通过实验获取误差源数据,利用数学方法和数学工具对数据进行加工处理,找到热与热变形之间的内在联系,从而建立热误差模型对误差进行预测和补偿.在误差补偿中,关键问题是建立高精度的误差预测模型,目前主要的误差模型有神经网络模型和支持向量机模型.

林伟青等[3-4]分别建立了最小二乘支持向量机热误差模型和在线最小二乘支持向量机热误差模型,取得了很好的补偿效果,模型的结构参数选择了常用的交叉验证法来寻优,但是交叉验证法需要大量的数据,且需要花费大量时间.雷春丽等[5]分别采用多元自回归方法和遗传径向基函数神经网络方法建立电主轴热误差预测模型,建议对短期预测精度要求高的情况选用自回归模型,而遗传神经网络模型更适合于对中长期预测要求高的情况.Abdulshahed等[6]将模糊神经网络系统应用在热误差建模上,建立了FCM的热误差补偿模型,该模型拥有人工神经网络和模糊聚类理论的多项优点,且具有较高的精度和鲁棒性.Echerfaoui等[7]在人工神经网络模型基础上提出软件式误差补偿新方法,提高了预测精度.虽然神经网络模型有不错的效果,但是神经网络建立热误差模型存在以下问题:模型训练需要大量的数据，易陷入局部最优，模型初始权值和阈值随机取值导致每次预测的结果产生变化.而支持向量机拥有很强的非线性映射能力,它将非线性问题转换为二次凸优化问题,解决了智能算法易陷入局部最优的问题[2].因此,本文提出利用支持向量机方法来解决机床热误差预测问题.

最小二乘支持向量机(least square-support vector machine,LSSVM)继承了支持向量机的优点,采用最小二乘线性系统作为损失函数,从而加快计算速度.但是,最小二乘支持向量机过度地依赖训练参数,训练参数直接决定着模型精度.因此,许多学者通过智能优化算法对训练参数进行迭代寻优,主要有模拟退火算法、遗传算法、粒子群算法等[8-11].

布谷鸟算法(cuckoo search,CS)采用莱维飞行机制,从而扩大了搜索范围，增强了种群的多样性,且更容易跳出局部极值[12].因此,本文提出采用布谷鸟算法优化最小二乘支持向量训练参数,建立基于布谷鸟算法优化最小二乘支持向量机的数控机床热误差模型.预测结果表明,该方法相比于LSSVM和萤火虫算法优化BP神经网络模型,提高了机床热误差预测效率和预测精度.

1 布谷鸟算法优化最小二乘支持向量机数学模型

1.1 布谷鸟算法优化最小二乘支持向量机的原理

回归支持向量机(SVM)属于二次凸优化方法,通过核函数φ(Xi,X)将非线性问题转换到高维特征空间成为线性问题,避开了局部极值[13].但是,SVM允许一定的误差存在,如图1所示，ε(超平面偏移量)带中的样本点不作为支持向量,导致模型预测精度低.在此基础上提出LSSVM.LSSVM将SVM中不等式约束改为等式约束,使所有样本点都是支持向量,且是以结构风险最小化为原则的核函数学习机器.因此,LSSVM能够提高计算精度,增强模型的泛化能力.

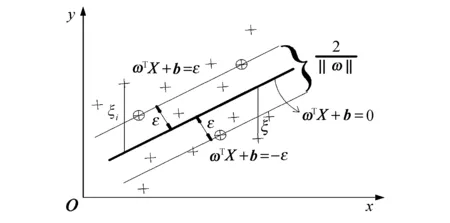
图1 ε带不敏感函数Fig.1 ε with insensitive function

特征空间中LSSVM模型可表示为

yi(X)=ωT·φ(Xi,X)+bi

(1)

式中：ω为权重因子；φ(Xi,X)为非线性映射核函数；b为偏置因子.

LSSVM数学模型为

(2)

式中：γ为惩罚因子,决定对超出误差样本的惩罚程度;ξi为松弛变量,决定样本拟合误差;‖*‖为任意表示距离的度量;l为样本个数.

通过拉格朗日函数求解:

(3)

式中：αi为拉格朗日乘子.

根据函数极值存在条件求解得：

(4)

消去式(4)中ω和ξ得线性系统：

(5)

式中:α=[α1,α2,…,αl]T;Y=[y1,y2,…,yl]T;L=[1,2,…,l]T;A=[φ(X1,X)T,φ(X2,X)T,…,φ(Xl,X)T].

令H=AAT+γ-1I,求解式(5)得：

(6)

求得最终的决策函数为

(7)

常见的核函数有:

式中:σ为核宽度;d为正数;β为缩放参数;θ为转换参数.

多项式核函数具有优越的全局性和强大的外推能力,且随着多项式次数d的递减,其外推能力逐渐增强.而Gauss径向基核函数具有优越的局部性,其内推能力随着核宽度参数σ的递减逐渐减弱.结合两类核函数各自的优点,找到具有很强的推广性和学习能力的混合核函数,表达式为

φmin=λφploy+(1-λ)φRBF

(8)

式中:φploy为多项式核函数;φRBF为Gauss径向基核函数;λ∈(0,1),随着λ的递增混合核函数的性能逐渐提高.

采用混合核函数的LSSVM模型需要确定λ、γ、σ这3个参数,因训练参数直接决定着模型精度，故LSSVM模型过度依赖训练参数.而CS算法主要优点是参数少、操作简单、易实现、随机搜索路径优(Levy随机飞行搜索机制)和全局寻优能力强等.因此,本文提出采用布谷鸟算法对参数进行迭代优化.

布谷鸟搜索算法根据寄生鸟类布谷鸟寄生育雏行为,模拟布谷鸟寻找最优鸟巢机理,用以有效求解最优化问题[14].王凡等[15]已通过建立CS算法的Markov链模型,理论证明了该算法可收敛于全局最优.

CS平均绝对误差函数为目标函数,即

(9)

式中：yp(t)和yr(t)分别为预测数据和实验数据;N为向量长度.

CS算法采用莱维飞行搜索方式更新鸟巢的位置,即

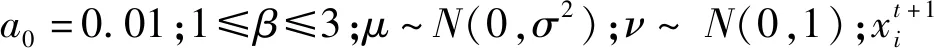
寻找到新的鸟巢后,计算新鸟巢的优劣度,用随机均匀分布的数与发现概率比较.发现概率大于随机数,保留该鸟巢,反之丢弃,重新购造新的鸟巢,即

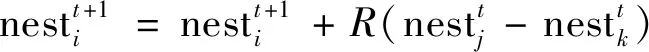
(12)

1.2 布谷鸟算法优化最小二乘支持向量机算法

采用布谷鸟算法优化最小二乘支持向量机(CS-LSSVM)进行数控机床热误差预测的建模过程如图2所示.优化步骤包括：

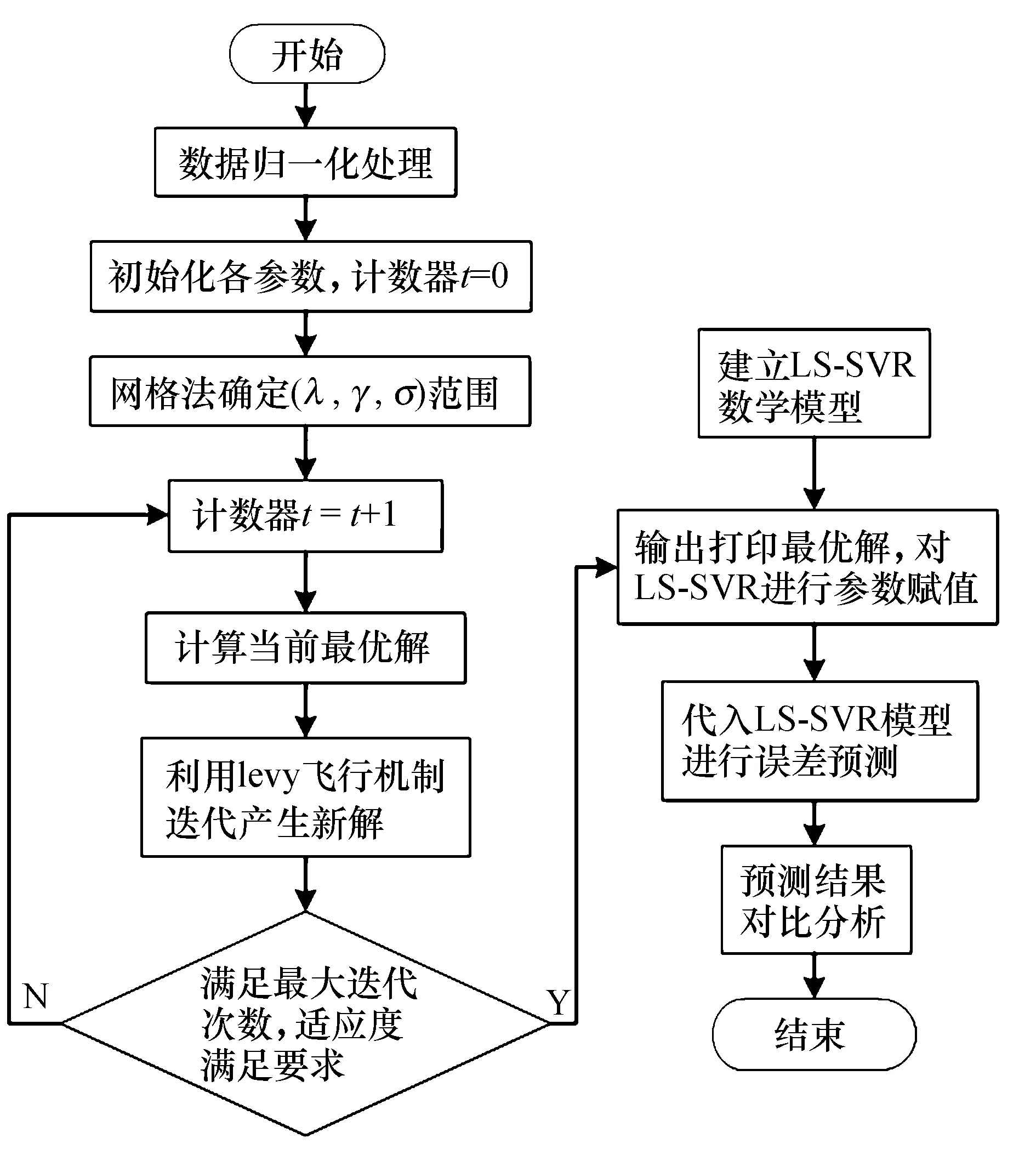
图2 CS-LSSVM预测流程Fig.2 CS-LSSVM prediction process

1)数据预处理.收集CS-LSSVM模型的训练样本和测试样本,进行归一化处理;

2) 初始化各参数.随机生成N个鸟巢的初始位置向量,定义目标函数和初始化函数,设置种群规模、最大迭代次数、最小误差要求、维数、发现概率;

3) 确定参数搜索范围.用网格搜索算法确定λ、γ、σ的搜索范围;

4) 找寻最优解.确定适应度函数,对自适应布谷鸟算法进行初始设置,根据布谷鸟算法机制式(10)找到鸟巢位置与拟合度的当前最优值,然后找出更新解与淘汰解,得到最优值;

5) 终止条件判断.当达到设置的最大迭代次数和最小误差要求后,算法停止搜索,输出的最优解即为LSSVM参数最优值,否则转至步骤4).

2 y轴热误差实验与误差数据处理

为验证CS-LSSVM模型的预测效果,对GMC2000A机床y轴的热误差进行了验证.在验证之前,为消除热误差数据之间的多元共线性,提出使用模糊C值聚类(fuzzyC-means algorithm,FCM)对数据进行聚类分析.

2.1 模糊C均值聚类算法基本原理

模糊C均值聚类算法是目前使用最多的模糊聚类算法之一[16].以往的硬聚类法是将各变量非0即1地严格划分到某一类中.而FCM是样本对类的隶属度不确定性的描述,即在0～1之间模糊划分,能够更好反映样本点的实际分类.

在FCM聚类算法中,设被分类对象的集合为X={x1,x2,…,xN},其中每个对象xk有n个特性指标,即xk=(x1k,x2k,…,xnk)T.如果要把X分成C类,则它的每个分类结果都对应C×N阶的Boolean矩阵U=[uij]C×N.若每类中UCi最大,就表示该样本点为此类的中心.对应的模糊C划分空间为

目标函数为

(13)

式中:i,j为类标号；m为聚类簇数,又称加权指数；xj为第j个样本,具有d维特征;μij为样本点xi属于j类的隶属度值;ci为i簇的中心,具有d维度.

根据Lagrange乘数法极值存在条件求得:

(14)

2.2 y轴热误差实验

本文引用文献[17]的误差实验.通过对GMC2000A机床结构的深入分析,选取该机床关键热源电机板(T1)、光栅尺(T2)、十字滑座左(T3)、横梁(T4)、十字滑座右(T5)、电机外壳(T6)、滑块(T7)、环境(T8)和螺母座(T9)这9个位置,如图3所示.在GMC2000A机床关键热源位置处布置9个Pt100 铂电阻温度传感器,用于测量9个关键点处的温度值,采用XL-80激光干涉仪测量和XSR90无纸记录仪记录y轴的定位误差.测量过程中,y轴总行程为3 400 mm,前后各预留200 mm余量,共3 800 mm.每当y轴伸进170 mm时,停留5 s,每间隔20 min记录1组定位误差数据,前后共记录了840个误差数据,40组温度数据(因为机床运行中温度值变化较小,所以每行程只采集1组温度值).测量期间,机床的速度设定为6～12 m/min.误差数据如图4所示.

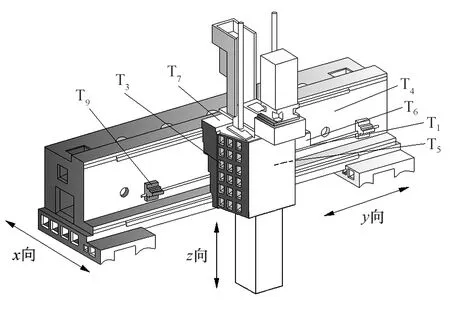
图3 y轴温度测量位置Fig.3 y-axis temperature measurement position

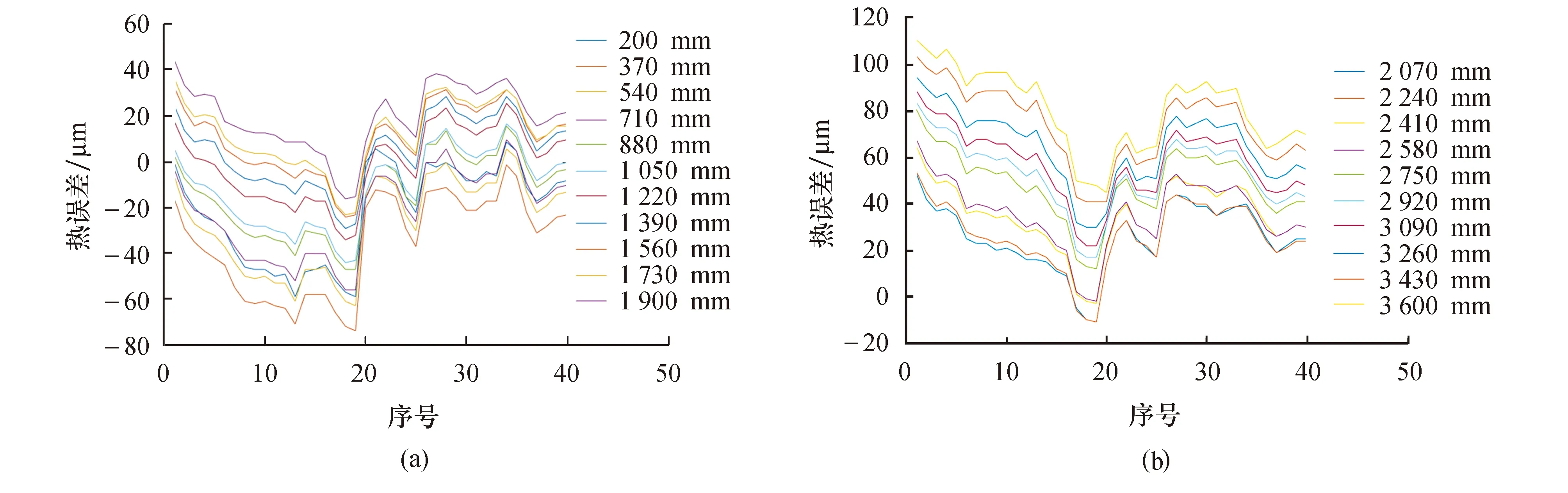
图4 数控机床y轴热误差Fig.4 y-axis thermal error of CNC machine tool

2.3 热误差数据的筛选

在数控机床热误差预测模型中,不同数量的温度敏感点会导致不同的预测结果[18].温度敏感点数量过多,会延长模型的计算时间,并且使得相近测点的输出信号存在多元共线性;温度敏感点数量过少,不能全面反应误差源之间的联系,进而导致模型精度变差.为了在多个温度测点中选出适当的测点数量,且必须保证信息系统的划分能力不变,需要对机床热误差的温度测点进行筛选,本文采用FCM对热误差数据进行筛选.

FCM算法的具体流程如下:

1) 初始化.给定聚类类别数C(2≤C≤N,N为样本点个数),设置迭代停止的阀值η,初始化聚类隶属度值U(0),设定迭代计数器z=0;

2) 根据式(14)计算ci,uij;

3) 判断迭代是否终止.若‖c(b)-c(b+1)‖<η,则算法停止输出,划分隶属度矩阵U和聚类原型C,否则转向第2)步;

4) 计算目标函数值.根据式(13)计算Jm,判断是否满足函数收敛条件,若满足则停止计算,否则返回第3)步;

5) 选取温度敏感点.分析得到的隶属度矩阵U,对温度数据进行分类,将各类中隶属度值最大的温度点作为本类温度敏感点.

首先对FCM参数初始化.设置最大迭代次数为50,隶属度最小变化量为1×10-6,‖*‖为欧式距离.加权指数m控制着模型在模糊类间的耦合程度,适当的m值能够抑制噪声,控制隶属度函数等.通过多次聚类分析,最终确定模糊权重指数m=1.5.基于此进行了模糊C均值聚类,温度点聚类结果如表1所列.

温度数据经聚类分组后,对聚类结果进行评价.最好的聚类结果本质要求类间关系疏远,类内关系精密.现依据聚类本质提出聚类结果有效性评价指标F(C),分子表示类内距离,分母表示类间距离.因此,评价指标F(C)越小,聚类效果最优.

(i,j=1,2,…,C,i≠j)

(15)

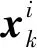
(16)

聚类结果如表2所列.

从表1可以看出：分3类时,FCM迭代次数最少,且隶属度都大于0.9;分2类和4类的迭代次数多,且个别点的隶属度值较小.从表2可以看出，F最小时分为3类.综上所述,最终确定划分为3类.其中，第1类中T8隶属度最大,第2类中T7隶属度最大,第3类中T5隶属度最大.因此,确定T5、T7、T8为聚类中心.

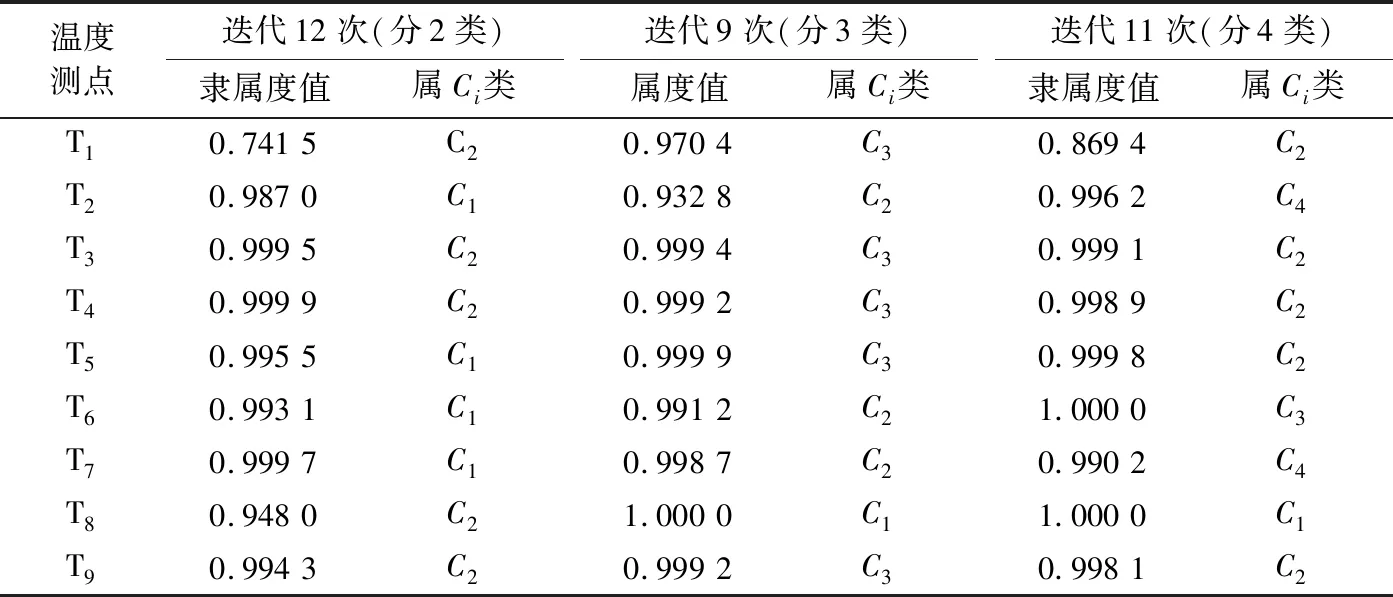
表1 FCM温度筛选结果Tab.1 Results of FCM temperature screening

表2 聚类有效性指标F值Tab.2 Cluster validity index F value

3 数控机床热误差建模与预测

3.1 CS-LSSVM热误差建模

1) 对CS-LSSVM模型的参数初始化.将通过FCM筛选得到的40组温度变量T5、T7和T8作为CS-LSSVM模型的输入,记为Xi,共120个数据;将y轴的40组定位误差数据作为CS-LSSVM模型的输出,记为yi,共840个数据.其中,(Xi,yi)的第15～30组数据用于测试.布谷鸟算法鸟巢数量N=30,被发现概率pa=0.25,寻优参数dim=3.

2) 由于模型的训练有较大波动,可能会导致预测误差值偏大,所以需要对数据进行归一化处理.归一化函数为

(17)

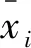
3) 热误差模型训练.将初始化的各项参数和归一化后的误差训练数据代入模型进行训练,寻优后的LSSVM模型关键参数值γ=10.430 4,σ=0.010 0,λ=0.728 6.

3.2 数控机床热误差预测与对比分析

用训练好的CS-LSSVM热误差模型对y轴定位误差进行预测.图5为BP神经网络模型的预测值与误差值,BP神经网络误差绝对值的平均值为8.065 4 μm.图6为经过交叉验证法优化LSSVM模型的预测值与误差值,LSSVM 误差绝对值的平均值为7.012 7 μm.图7为经过萤火虫算法优化BP神经网络模型的预测值与误差值,FABP神经网络误差绝对值的平均值为3.792 3 μm.图8为经过布谷鸟算法优化混合核最小二乘支持向量机模型的预测值与误差值,CS-LSSVM误差绝对值的平均值为1.799 5 μm.机床行程中370 mm处的预测值与真实值对比如图9所示和表3所列.

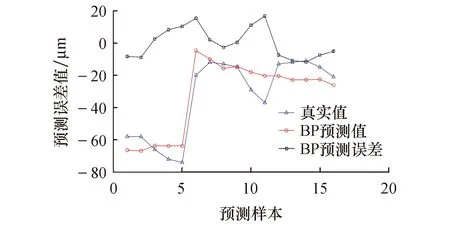
图5 BP神经网络预测结果Fig.5 BP neural network prediction results

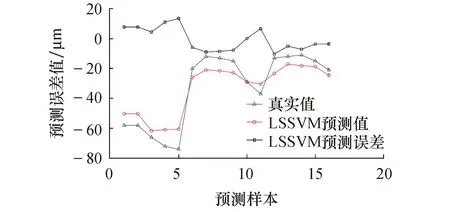
图6 LSSVM预测结果Fig.6 LSSVM prediction results

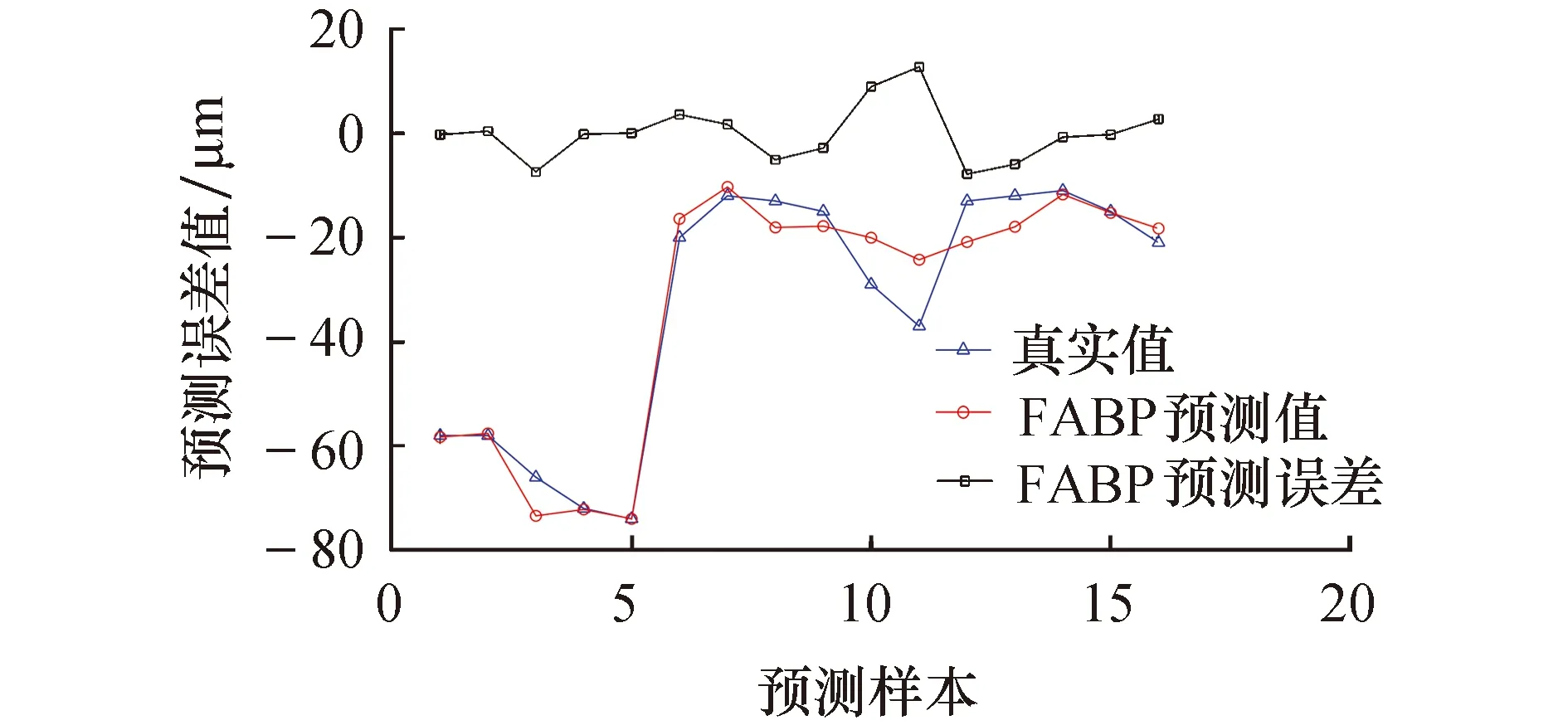
图7 FABP神经网络预测结果Fig.7 FABP neural network prediction results

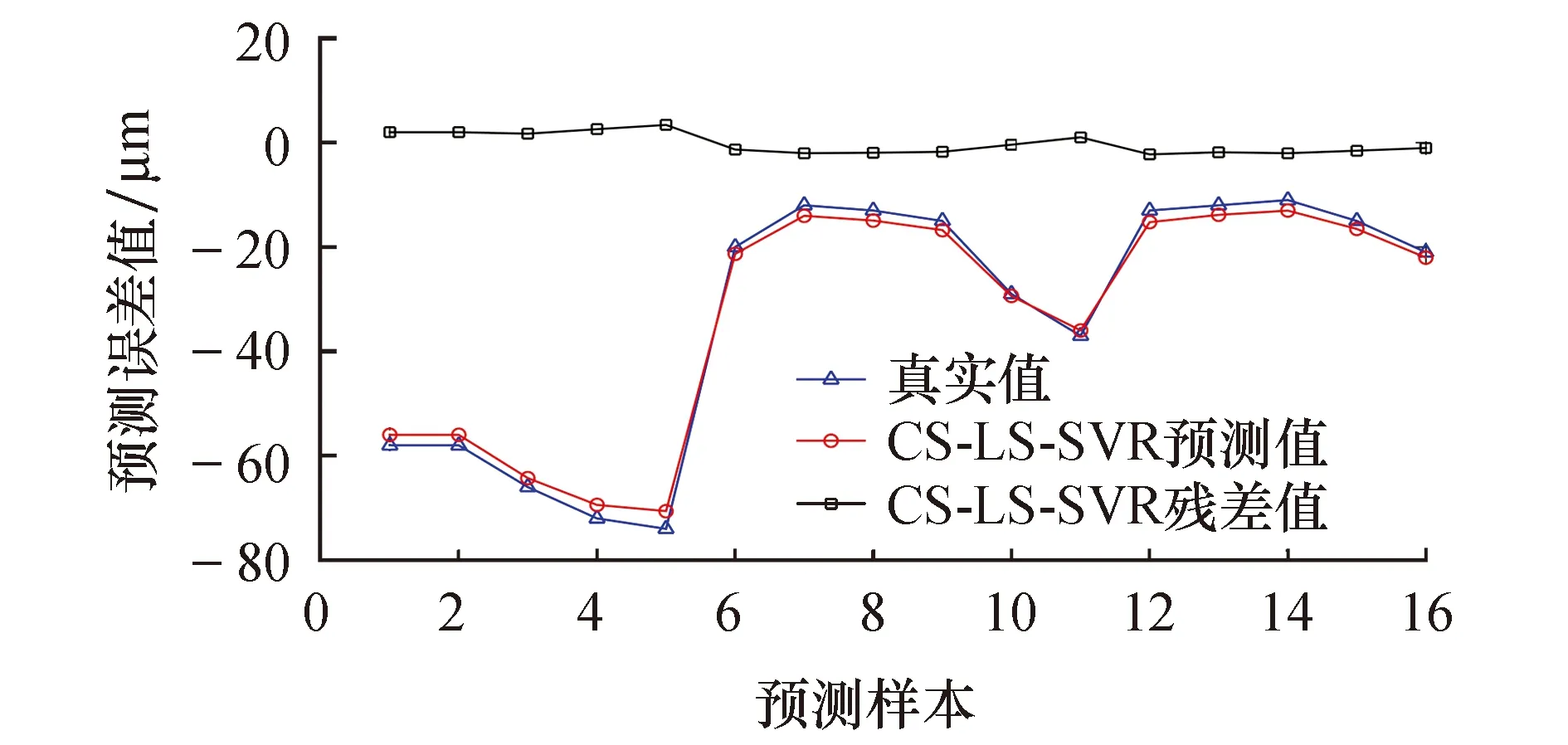
图8 CS-LSSVM预测结果Fig.8 CS-LSSVM prediction results

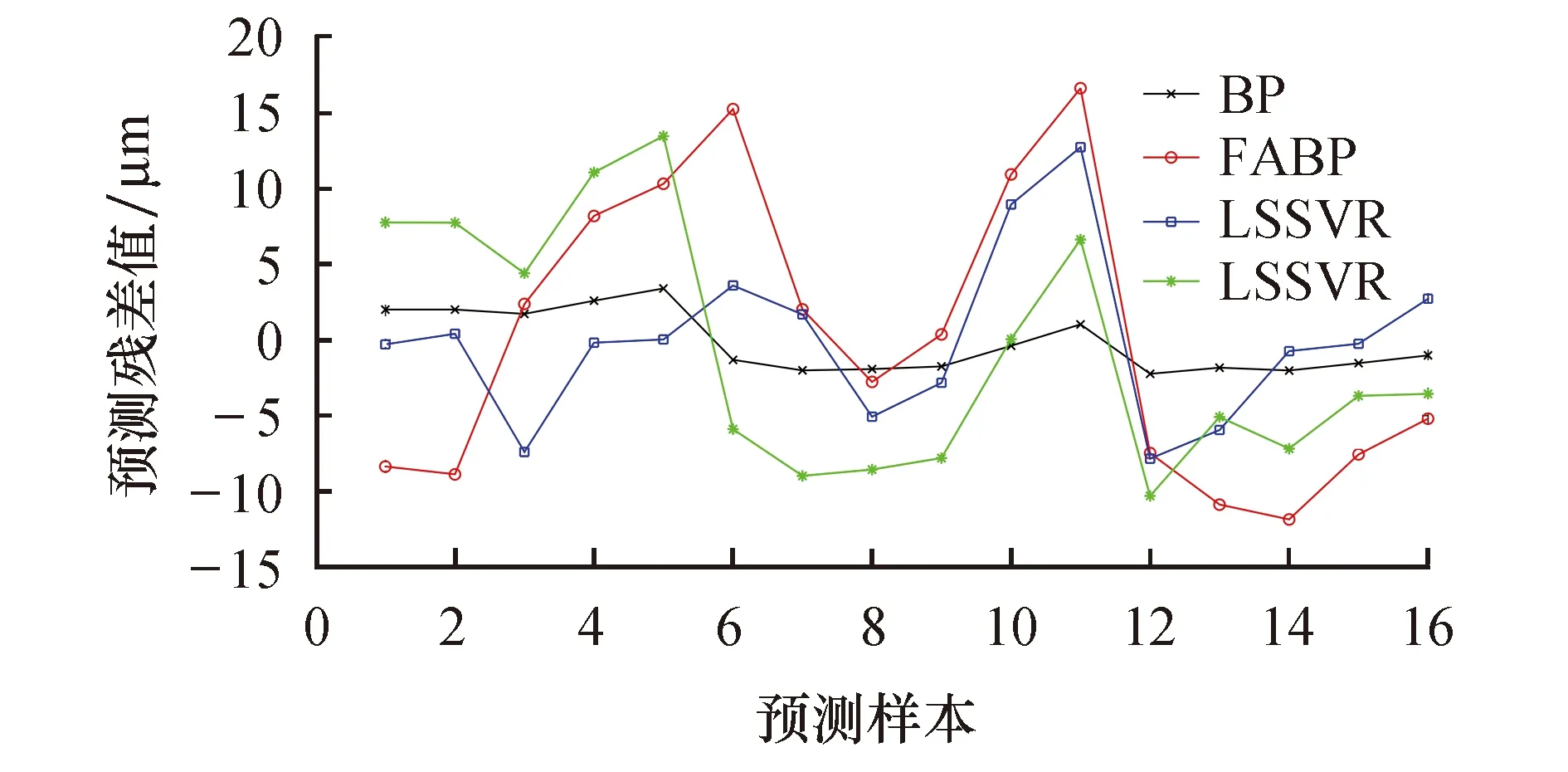
图9 多种误差模型预测后残差对比 Fig.9 Comparison of residuals after prediction of multiple error models

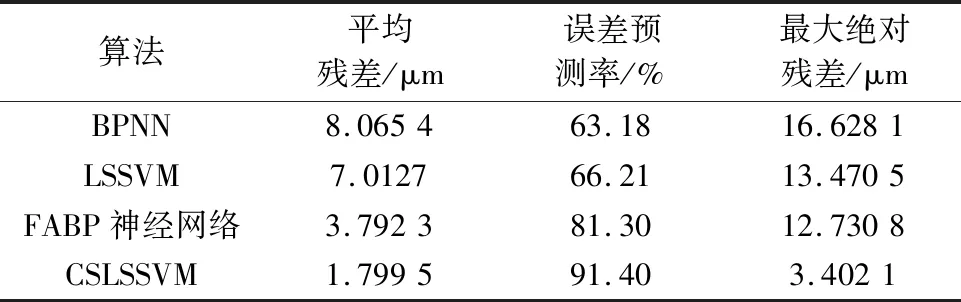
表3 多种误差模型预测结果对比Tab.3 Comparison of prediction results of multiple error models

从图6～9可以看出,BP神经网络模型、LSSVM模型和FABP神经网络模型具有一定的预测效果,但这3种模型在机床启动到稳定工作的过程中,对误差出现跳动不能迅速地拟合,而CS-LSSVM模型能够对误差跳动实现实时追踪.

从图9和表3可以看出,CS-LSSVM误差模型有相对较好的预测结果.在平均残差方面,CS-LSSVM模型的平均残差为1.799 5 μm,相比BP神经网络模型减小了6.265 9 μm,相比LSSVM模型减小了5.213 2 μm,相比FABP神经网络模型减小了1.992 8 μm;在误差预测率方面,CS-LSSVM模型的误差预测率为91.4%,相比BPNN模型提高了28.22%,相比LSSVM模型提高了25.19%,相比FABP神经网络模型提高了10.1%;在最大绝对残差方面,CS-LSSVM模型的最大绝对残差为3.402 1 μm,相比BPNN模型减小了13.226 μm,相比LSSVM模型减小了10.068 4 μm,相比FABP神经网络模型减小了9.328 7 μm.因此,CS-LSSVM模型能够很好地对GMC2000A机床y轴进行热误差预测,且该模型拥有很高的预测精度.

4 结论

为了提高数控机床热误差模型预测精度,本文基于布谷鸟算法，通过莱维飞行机制实现全局寻优的优点,提出了布谷鸟算法优化混合核最小二乘支持向量机的热误差建模方法.主要结论有:利用FCM选取了十字滑座右(T5)、滑块(T7)和环境(T8)作为热误差模型的输入;在支持向量机中引入了混合核函数,增强了误差模型的推广性和学习能力;利用布谷鸟算法选取了惩罚因子γ、核宽度因子λ和混合核函数权值因子σ的最优值,从而建立了基于布谷鸟算法优化最小二乘支持向量机的数控机床热误差模型;通过对y轴的热误差预测,且与BP神经网络、萤火虫算法优化BP神经网络、基于K折交叉验证法优化最小二乘支持向量机的热误差模型预测结果进行了对比,结果表明，CS-LSSVM模型具有更高的精度和较好的泛化能力,对数控机床热误差预测有较大的帮助.