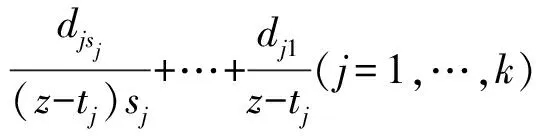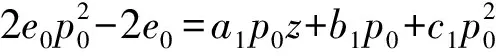差分Painlevé方程组解的存在性和增长级

邱 迪，蒋业阳

(江西科技师范大学数学系，江西 南昌 330038)

1 引言与主要结果

在本文中，我们假定读者熟悉Nevanlinna理论的基本概念、符号和复差分方程领域的一些基础知识，详细内容参见[1,2]。在文献[3]中我们了解到Painlevé方程与许多数学和物理问题密切相关，并且许多解析的、几何的和代数的性质不断被发现，1893年，E.Picard提出下列方程是否具有Painlevé性质的代数微分方程的重要问题。

ω″=f(z,ω,ω′)

(1.1)

Painlevé P.和他的合作者们解决了这一问题，他们指出若方程(1.1)具有Painlevé性质，则可划归为五十类典型的方程，但仅有六类方程产生新的超越函数，这六类方程就是著名的Painlevé Ⅰ-Ⅵ方程。众所周知离散的Painlevé Ⅲ方程在所有的离散Painlevé方程中占有特殊的地位，这是第一个在某些物理应用中被发现能产生超越函数的方程。发现不久之后，文献[4-5]就证明了该方程具有可积性，这为我们研究Painlevé Ⅲ方程奠定了良好的基础。

1991年，Ramani A.等[6]首先引进了Painlevé Ⅲ方程的离散形式：

(1.2)

随后Grammaticos B.等[7]对方程(1.2)进行一系列的变量代换，得到了两种不同的连续极限形式

(1.3)

和

(1.4)

显然，连续的Painlevé Ⅲ方程有两种不同的规范形式，我们可通过方程的有效参数的个数来区分。众所周知，离散的Painlevé Ⅲ方程是其连续极限对应的完美模拟。正如文献[8]所示，下列方程

(1.5)

正是方程(1.3)和(1.4)的自然离散模拟。更有趣的是文献[8]还介绍了方程(1.5)可重写成一组方程组

其中θ和κ是常数,κ和η关于n是线性的。这是一个深刻的结果，因为方程组中的每一个方程都有离散Painlevé Ⅱ方程的形式。

由于连续变量和离散变量的本质不同，复差分方程解的性质的研究成为时下复分析的热点之一。例如，在2000年，Ablowitz、Halburd和Herbst等[9]根据离散方程的可积性把离散方程看作是复平面上的时滞方程，他们认为所有的离散差分方程都有明显的分析方法，因此可使用复分析的方法来研究，特别是Nevanlinna的值分布论的方法。正是因为这种方法的渗透和应用，差分和差分方程从实数域发展到复数域成为了必然结果。在复数域上的扩展可帮助我们获得更本质的认识，许多数学工作者如Halburd,Korhonen以及Ronkainen等人[10-14]做了许多关于差分Painlevé方程的解的研究，特别地，Ronkainen在2010年研究了差分Painlevé Ⅲ方程的亚纯解得出了下述定理：

定理A[12]假设方程

ω(z+1)ω(z-1)=R(z,ω)

(1.6)

有一个超级小于1的可允许的亚纯解ω，其中R(z,ω)是关于ω的不可约的有理函数，关于z的亚纯函数，那么ω要么满足一个差分Riccati方程

其中α(z),β(z),γ(z)是代数体函数，要么方程(1.6)可转化为下列方程之一：

ω(z+1)ω(z-1)=

(1.7)

(1.8)

(1.9)

ω(z+1)ω(z-1)=h(z)ω(z)m

(1.10)

在(1.7)式中，系数满足κ(z)λ(z+2)λ(z-1)=κ(z-1)λ(z)λ(z+1)，λ(z+1)μ(z)=κ(z),λ(z-1)μ(z+1)，κ2(z)μ(z+1)μ(z-1)=μ2(z),和下列情况之一：

(1)η≡1,ν(z+1)ν(z-1)=1,κ(z)=ν(z)；

(2)η(z+1)=η(z-1)=ν(z),κ(z)≡1。

在(1.8)式中，系数满足η(z)η(z+1)和λ(z+2)λ(z-1)=λ(z)λ(z+1)。

在(1.9)式中，系数满足下列情况之一：

(1)η(z)≡1并且要么λ(z)=λ(z+1)λ(z-1)要么λ(z+3)λ(z-3)=λ(z+2)λ(z-2)；

(2)λ(z+1)λ(z-1)=λ(z+2)λ(z-2),η(z+1)λ(z+1)=λ(z+2)η(z-1),η(z-1)η(z)=η(z+2)η(z-3)；

(3)η(z+2)η(z-2)=η(z)η(z-1),λ(z)=η(z-1)；

(4)η(z)λ(z)=η(z+2)η(z-2),λ(z+3)λ(z-3)=λ(z+2)λ(z-2)λ(z)。

在(1.10)式中，h(z)是代数体函数并且m∈Z,|m|≤2。

在此之后，自然就会更进一步想到复差分Painlevé方程组的解的存在性上去，更关键的是我们注意到离散Painlevé Ⅲ方程的自然离散模拟可化为含PainlevéⅡ方程的方程组，因此结合定理A我们考虑更一般的差分Painlevé方程组的解的情况。我们主要考虑下列方程组

(1.11)

其中α(z),β(z),γ(z),a(z),b(z),c(z)都是关于z的多项式。

但在这篇文章中我们仅研究了方程组(1.11)的一种特殊情况α(z)=a(z)=0,β(z),b(z)是关于z的线性函数，γ(z),c(z)是常数，因此我们的方程可写为

(1.12)

其中a1,a2,b1,b2,c1,c2都是常数且a1,a2不等于0。

定理1.1设a1,a2均为非零常数，则差分方程组(1.12)不存在有理函数解。

例1在方程(1.12)中，设a1=a2=0，b1=-1，b2=c1=c2=1则方程组

定理1.2若c1≠±2且c2≠±2,设(x(z),y(z))是差分方程组(1.12)的一组有限级超越亚纯解，则我们有ρ(x)=ρ(y)≥1。

注记1在定理2的证明中我们发现若(x(z),y(z))是方程组(1.11)的一组解并且系数α(z),β(z),γ(z),a(z),b(z),c(z)分别是x(z),y(z)的小函数，那么也一定有ρ(x)=ρ(y)。

2 引理

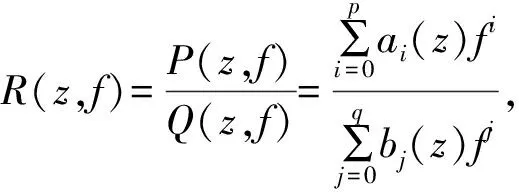
那么我们有T(r,R(z))=max{p,q}T(r,f)+S(r,f)。

引理2.2[17]设f(z)是一个ρ=ρ(f),ρ<∞的亚纯函数,并且设η是一个固定的非零复数，那么对于∀ε>0，我们有：

T(r,f(z+η))=T(r,f)+O(rρ-1+ε)+O(logr)

引理2.3[2]设g在平面上是一个级小于1的超越亚纯函数。设h>0,则存在一个ε集合Ε使得当z在C/Ε内趋于∞时，满足|c|

那么g在|ξ-z|≤h内没有极点或零点。

3 定理的证明

(3.1)

其中e0,e1,…,em是常数。

同理，我们可把y(z)表示为

(3.2)

其中p0,p1,…,pn是常数。

对于(3.1)式,我们可断定e1=…=em=0。如若不然，我们可假设em≠0(m≥1)，则当z充分大时，有

x(z)=emzm(1+o(1)),x(z+1)=em(z+1)m(1+o(1))=em(1+o(1))

(3.3)

对于(3.2)式，我们也断定p1=…=pn=0，如若不然我们可假设pn≠0(n≥1),当z充分大时，则有

y(z)=pnzn(1+o(1)),y(z-1)=pn(z-1)n(1+o(1))=pn(1+o(1))

(3.4)

将(3.3)式和(3.4)式代入差分方程组(1.12)得到：

(3.5)

和

(3.6)

由于m≥1,因此(3.5)式左右两边的次数不相等，故出现矛盾。

由于n≥1,因此(3.6)式左右两边的次数不相等，也出现矛盾。

因此，e1=…em=p1=…pn=0。

接下来，我们证明e0=0,p0=0,如若不然，e0≠0,p0≠0,则当z充分大时，我们有

(3.7)

同理有

(3.8)

(3.9)

不妨设

s(z)=szk+sk-1zk-1+…+s0

(3.10)

h(z)=hzt+ht-1zt-1+…+h0

(3.11)

m(z)=mzl+ml-1zl-1+…+m0

(3.12)

n(z)=nzu+nu-1zu-1+…+n0

(3.13)

其中s,sk-1,…,s0,h,ht-1,…,h0,m,ml-1,…,m0,n,nu-1,…,n0均为常数且shmn≠0显然有k

h(z)s(z+1)m(z)2+h(z+1)s(z)m(z)2-n(z)2h(z)s(z+1)-s(z)n(z)2h(z+1)=a1zn(z)h(z)h(z+1)m(z)+b1n(z)h(z)h(z+1)m(z)+c1m(z)2h(z)h(z+1)

(3.14)

和

m(z)n(z-1)s(z)2+n(z)m(z-1)s(z)2-m(z)n(z-1)h(z)2-n(z)m(z-1)h(z)2=a2zn(z-1)s(z)h(z)+b2n(z)n(z-1)s(z)h(z)+c2n(z)n(z-1)s(z)2

(3.15)

根据(3.14)式左右两边的次数关系我们有：l-u+1=k-t。但根据(3.15)式左右两边的次数关系我们又有：k-t+1=l-u这显然是不可能的。因此差分方程组(1.12)不存在有理函数解。

定理1.2的证明我们先证ρ(x(z))=ρ(y(z)).由差分方程组(1.12)我们有：

(3.16)

(3.17)

对于(3.16)式和(3.17)式右边的式子运用引理2.1得：

(3.18)

(3.19)

根据特征函数的运算性质，我们得到：

T(r,x(z+1)+x(z))≤T(r,x(z+1))+

T(r,x(z))

(3.20)

T(r,y(z)+y(z-1))≤T(r,y(z-1))+

T(r,y(z))

(3.21)

根据引理2.2有：

T(r,x(z+1))+T(r,x(z))=2T(r,x(z))+O(rρ-1+ε)+O(logr)

(3.22)

T(r,y(z))+T(r,y(z-1))=2T(r,y(z))+O(rρ-1+ε)+O(logr)

(3.23)

由(3.16)，(3.18)，(3.20)和(3.22)有

2T(r,y(z))+S(r,y(z))≤2T(r,x(z))+

O(rρ-1+ε)+O(logr)

(3.24)

由(3.17)，(3.19)，(3.21)和(3.23)有

2T(r,x(z))+S(r,x(z))≤2T(r,y(z))+

O(rρ-1+ε)

(3.25)

由增长级定义，以及式子(3.24)和(3.25)可得ρ(x(z))=ρ(y(z))。不失一般性，我们令ρ(x(z))=ρ(y(z))=ρ，现要证ρ≥1，我们不妨假设ρ<1,则通过引理2.3可知存在一个ε-集合E，使得在CE中z→∞.那么我们有

x(z+1)=x(z)(1+o(1))

(3.26)

y(z-1)=y(z)(1+o(1))

(3.27)

将(3.26)和(3.27)代入差分方程组(1.12)得

经计算得：

(3.28)

和

(3.29)

在(3.28)式中，我们令

P(z,y(z))=[2(c12-4)y(z)5+4c1(a1z+b1)y(z)4+2((a1z+b1)2+8)y(z)3-8y(z)](1+o(1))Q(z,y(z))=[2c2(a2z+b2)+c2c12]y(z)4+[2(a1z+b1)(a2z+b2)+2c1c2(a1z+b1)]y(z)3+[c2(a1z+b1)2-2c1(a2z+b2)]y(z)2-2(a1z+b1)(a2z+b2)y(z)

那么我们有P(z,y(z))=Q(z,y(z))，但由于c1≠±2且y(z),x(z)都是超越的。显然有

T(r,P(z,y(z)))=5T(r,y(z))+S(r,y(z))

T(r,Q(z,y(z)))=4T(R,y(z))+S(r,y(z))

这是一个矛盾。同理，对于(3.29)式也有同样的矛盾。因此ρ≥1。