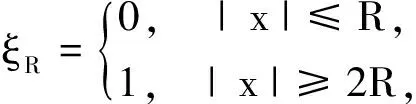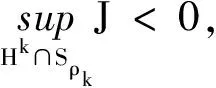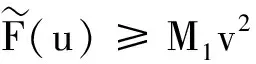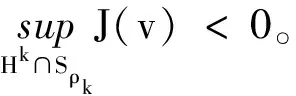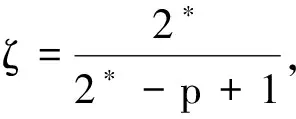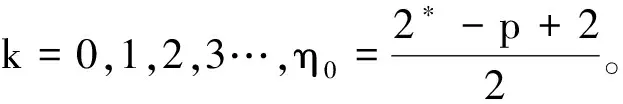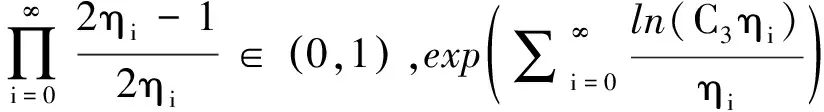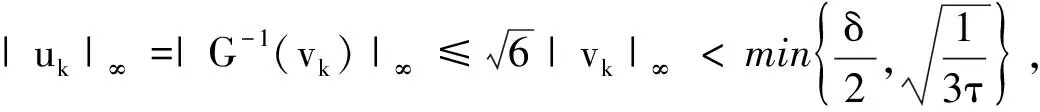拟线性Schrödinger方程解的多重性
朱文杰,陈春芳
(南昌大学数学系,江西 南昌 330031)
1 引言与主要结果
在本文中,我们考虑以下拟线性Schrödinger方程
(1)
解的多重性。其中V,K∈C(RN,R),f(u)在u=0的邻域内有定义,N≥3且τ>0。要求方程(1)的解,就转化为求Schrödinger方程
i∂tψ=-Δψ+W(x)ψ-l(|ψ|2)ψ+
(2)
的孤立波解,其中ψ:RN×R→C,W:RN→R为位势函数,l和ρ:R→R为实函数。当选取不同的函数ρ时,此方程可以应用在物理学、光学、动力学等领域中,见文献[1-4]。如果方程(2)具有ψ(x,t)=exp(-iEt)u(x)的形式且满足ρ(s)=s时,则方程(2)可转化成下述椭圆型方程
(3)
其中E∈R,V(x)=W(x)-E且h是一个新的非线性项。
当方程(3)中的τ>0时,由于非凸项“Δ(u2)u”的出现,与方程(3)所对应的能量泛函可能没有合适的工作空间使其是定义良好的并且是属于C1的。为了解决这个困难,Alves等人在文献[5]中采用变量替换方法求解方程(3),同时结合山路引理和Moser迭代方法,证明了当τ∈(0,τ0)时,方程(3)正解的存在性,其中τ0是一个很小的正数。后来,Wang和Li[6]证明了带有临界增长的拟线性Schrödinger方程正解的存在性。关于此种情形的其他结果可参考文献[7-10]。
最近,许多学者关注于考虑含有局部项的拟线性Schrödinger方程的解的存在性,也就是考虑非线性项h(t)只在t=0的附近有定义的情形。Huang和Jia[11]考虑了带有超临界拟线性Schrödinger椭圆方程,并分别讨论了在三种位势(紧位势、井位势、周期位势)条件下的正解的存在性。Bao和Cheng[12]使用Clark定理得到具有如下形式方程
-Δu+V(x)u-Δ(u2)u=g(x,u),x∈RN
多解的存在性,其中非线性项g(x,u)在原点附近是次线性增长的。与文献[13-14]不同的是,此方程多解的存在性只有在N=3或N=4的时候才成立,这是因为在做L∞估计时要满足迭代运算所导致的。更进一步,他们所得的弱解收敛到0。
受以上文献启发,本文主要解决以下两个问题:
(Q1):与文献[12]对比,我们是否可以考虑非凸项“Δ(u2)u”的系数为正的情况,也即是方程(1)中τ>0情形,并且非线性项f只在原点附近有定义时解的存在性?
(Q2):如果我们把文献[11]中的非线性项是局部超线性增长的改成局部次线性增长,那这个问题的解还会存在吗? 特别地,也会类似文献[12]需要对空间维数N限制吗?
本文采用文献[12]的思路研究方程(1),我们对方程(1)中的位势函数V,K和非线性项f做出以下假设:
(V)0≤α≤V(x)≤β<∞,x∈RN,其中α,β是常数;
(f1)存在δ,M>0,p∈(1,2)使得f∈C((-δ,δ),R)是奇函数且|f(t)|≤M|t|p-1;
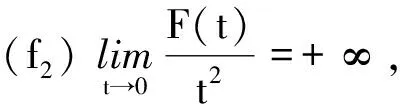
(K)0 本文的主要结果如下: 定理1.1假设(V),(f1)-(f2)和(K)成立。则方程(1)存在无穷多个负能量解。 这一节介绍本文所需要的空间和截断函数。首先介绍本文的工作空间为 H1(RN):={u∈L2(RN):∇u∈L2(RN)} 其范数为 通常,|·|s表示空间Ls(RN)的范数。C,Ci表示常数(i=1,2,3…),不同位置可能不相同。 (4) 接下来,我们考虑以下修正方程 (5) 解的存在性。方程(5)所对应的能量泛函为 (6) 的解的存在性,其中g(s):R→R且 现在我们定义 易知反函数G-1存在且是一个奇函数。下面,我们给出函数g,G-1的一些性质。 引理2.1[5]函数g,G-1满足: 接下来,我们采用以下变量代换 则 由引理2.1,我们得到泛函J在H1(RN)是定义良好的且J∈C1(H1(RN),R)。另外,对任意的ω∈H1(RN)有 因此,想要求方程(5)的弱解,我们只需要讨论半线性椭圆方程 的弱解。 在本节中,我们采用Clark定理来证明我们的结果。 定理3.1[15]设X是一个Banach空间,Ψ∈C1(X,R)。如果Ψ满足(PS)条件且 (a)Ψ(-u)=Ψ(u),Ψ(0)=0且Ψ有下界; 则以下结论至少有一条成立: (1)存在临界点序列{uk},使得对任意的k都有Ψ(uk)<0,并且当k→+∞时有‖uk‖→0; (2)存在r>0,使得对∀s∈(0,r),都有一个临界点u满足‖u‖=s且Ψ(u)=0。 下面,我们说明泛函J满足Clark定理的所有假设条件。 引理3.2假设(V),(f1)-(f2)和(K)成立。则泛函J有下界且满足(PS)条件。 证明由(4),(K),引理2.1、Hölder不等式有 则根据Sobolev嵌入不等式得到 又因为1 下证泛函J满足(PS)条件。令{vn}是一个(PS)序列,即当n→+∞时,有 |J(vn)|≤c,J′(vn)→0 显然当n→+∞时,有on(1)=〈J′(vn)-J′(v0),vn-v0〉,即 (7) 对任意取定的R>0,令ξR∈C∞(RN,[0,1])满足 on(1)= (8) 接下来,由引理2.1,Hölder不等式以及{vn}是有界的可知 (9) 和 (10) 成立。联立(8)-(10)有 然后再根据条件(V)和引理2.1,当R→+∞时,则有 (11) 又因为v0∈L2(RN),则我们可以取R0>0足够大使得 (12) 由(11)、(12)以及局部是紧嵌入的可知 也就意味着当n→+∞时,在L2(RN)中有vn→v0。 接下来,再次利用条件(K)、(4)以及引理2.1和Hölder不等式,我们得到 (13) 同理有 (14) 再由中值定理可得 (15) 最后,由(7)和(13)—(15)知 引理3.4令v是泛函J的一个临界点,则存在与v,τ无关的常数C*使得|v|∞≤C*。 证明因为v∈H1(RN)是泛函J的一个临界点,则对任意对φ∈H1(RN)有 (16) 令T>0,定义vT:=max{-T,min{v,T}}。取φ=|vT|2(η-1)v,其中η>1。容易验证φ∈H1(RN),因此我们把φ代入(16)有 根据vT的定义,我们知道上式等号左边第二项是非负的。 通过(4)和引理2.1,我们得到 (17) (18) 令T→+∞,由(17)、(18)、Hölder不等式和Sobolev不等式可知 和 下面,我们按照以上方法依次迭代下去,则有 然后令k→+∞可得 最后,由H1(RN)→L2*(RN)以及v的有界性可知|v|∞≤C‖v‖≤C*,其中C*与v,τ无关。 注记1从以上证明过程可以看出,与文献[5-6]相比,我们不需要把参数τ限制在一个很小的范围内,也即是说,参数τ可以为一个取定的数。2 预备知识
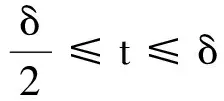
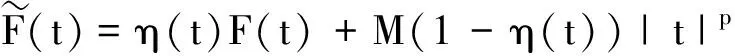

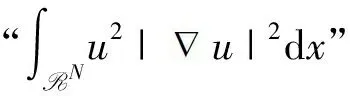
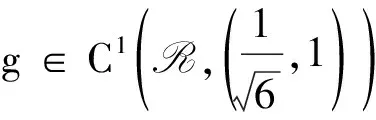
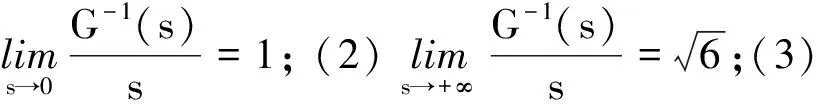
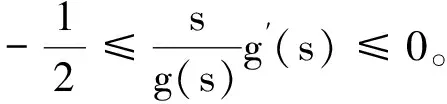
3 主要结果的证明