基于智能算法的无人集群防御作战方案优化方法

马也，范文慧，常天庆

(1.陆军装甲兵学院 兵器与控制系，北京 100072;2.清华大学 自动化系，北京 100084)

0 引言

无人集群的概念来源于无人机集群的研究，随着人工智能及自动化技术的进步，无人机器人、无人机、无人车及其他无人装备迅速发展，使得无人集群的种类范围大大扩展。由于无人集群具有装备及可完成任务数量多、无需人在环、可自主协同、无中心更灵活的组织方式、可方便回收等特点，受到美国为首等强国的高度重视，将其发展为无人集群系统(USS)并应用在军事中，成为未来战争的重要作战形式之一。目前，有专家在联合作战、协同侦察和战场通信等军事领域中研究探索无人集群系统的应用潜力。无人集群系统弥补了单一无人装备战斗力不足，可完成任务单一等问题，智能体(Agent)仿真技术中的Agent同样具有协同合作、自主性及与环境互动的能力。同时，Agent技术可应用在强化学习等多种智能算法中。将无人集群技术与Agent技术相结合，能够扩展无人集群的研究方法及思路。

无人集群的自主兵力部署及协同任务分配是无人集群作战的重点研究方向之一，是其自主及适应性的体现。在防御作战中，利用有限的兵力发挥最大的作战效能是防御作战中的研究疑难点，高效合理的兵力部署是实现其目标的手段。针对兵力部署问题，多使用粒子群优化算法、遗传算法、Memetic算法、线性规划算法等多种智能算法进行优化。以上方法存在模型构建复杂、阵地区域及武器种类单一、算法有早熟及局部最优、未对结果进行进一步论证测试等问题。

无人集群任务分配是任务规划的一部分，能够协调集群的一致性，保证高效完成作战任务。目前的作战任务分配领域大多以人为主，根据战场经验进行规划，而无人集群作战使作战方式逐步无人化，由此任务分配算法的研究逐步引起学者的关注。其中Agent技术与任务规划结合的方法取得较多成果，主要成果有基于马尔可夫过程的Agent任务分配算法，可以解决机器人在位置环境中的任务规划问题；基于Agent技术的分层任务规划方法，可以解决局部个体的任务分配方式等。上述方法的任务分配效率不高，随着强化学习算法在智能决策方面的突出表现，将其引用可突破任务分配问题的瓶颈。其中效果较好的强化学习算法有Team-Q算法、Distributed-Q算法等Agent技术任务分配方法。这些方法均从个体的角度进行考虑，未能协调多个个体并独立完成任务的问题。

本文针对无人集群作战的重点构建防御作战情景下的无人集群作战仿真模型。从作战方案中的兵力部署及任务分配两个方面，提出一种自适应遗传算法来解决无人集群兵力部署问题，对算法的目标函数及相应参数进行改进，提高算法性能，完成无人集群的战场兵力部署。为进一步验证算法的结果，提出一种基于深度强化学习的无人集群任务分配方法。增加自适应调节权重因子，根据算法运行效果实时调整Q值并得出无人集群防御作战结果。通过上述算法对无人集群防御作战的优化，使防御作战成功率得到提高。

1 无人集群防御模型

兵力部署及任务分配为无人集群作战中的重点研究方向之一，合理的兵力部署可使有限的兵力发挥出最高的作战效能，有利于提高我方作战胜率。无人集群任务分配能够协调集群一致性，保证作战任务合理高效分配，更好地完成作战任务。针对无人集群作战中兵力部署和任务分配这两个重点方面，构建无人集群防御作战模型。模型架构如图1所示。

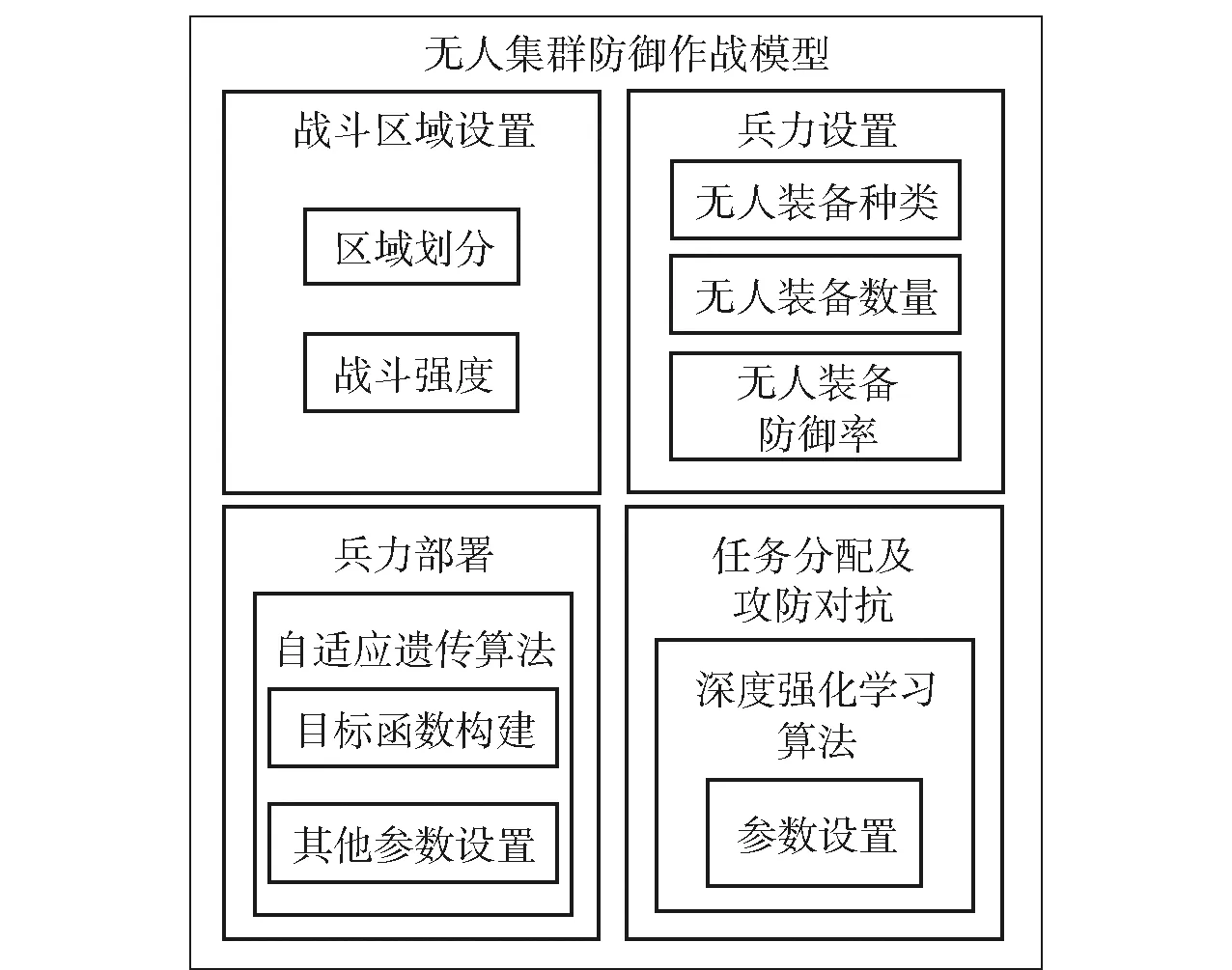
图1 无人集群防御作战模型架构Fig.1 Unmanned swarm defensiv combat model architecture

由图1可见，无人集群防御作战模型主要由四部分构成，分别用于对战斗区域及兵力进行设置、构建目标函数、完成自适应遗传算法的设置解决兵力部署、通过强化学习算法完成防御任务分配及攻防对抗。

1.1 战斗区域及兵力规划

作战过程中，防御方会根据地形、敌方主攻方向、防御目标等因素划分战斗区域。综合考虑各方影响，在某些区域集中兵力进行高强度战斗，某些区域作为佯攻区域。假设一个防御作战战场分为(≥1)个战斗区域，每个战斗区域内包含(≥1)个防御重点。设战斗强度因数为(≤1)，作战重要程度因数为。模型通过战斗强度因数表示战斗区域的战斗强度，在主要战斗区域，=1，非主要战斗区域<1，相同战斗区域内的不同防御要点其战斗强度因数相同。通过战斗区域的作战重要程度因数表示作战区域的作战重要程度。战斗区域的战斗强度及作战重要程度都将对兵力部署方案造成一定影响。

包含(=1,2，…，)个防御重点的第个战斗区域的作战重要程度因数计算方法如(1)式所示：

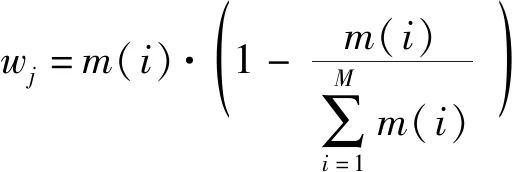
(1)

式中：为第个战斗区域的作战重要程度因数；()为第个防御重点的战斗强度因数。

无人集群装备的战斗能力通过单件装备的武器效能指数量化，武器效能指数是度量不同型号种类武器装备战斗能力的标准。模型中的无人集群装备种类及兵力效能指数参考历史数据及现有情况分析分为5种类型，包括类步枪型、类机关枪型、类迫击炮型、类榴弹炮型及类坦克型无人装备。无人集群装备类型、数量及单件武器战斗效能指数如表1所示。

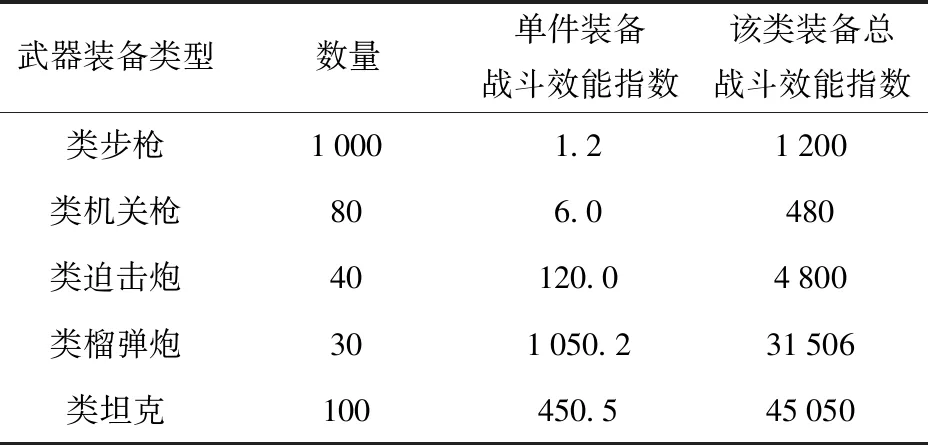
表1 无人集群装备兵力设计Tab.1 Unmanned swarm equipment force design

单件无人集群装备战斗效能指数为，该类装备总战斗效能指数为与该类装备数量的乘积。为方便模型构建及后续优化算法的使用，将每件无人集群装备视作一个Agent。模型将根据武器效能指数决定装备有效防御战区的概率并得出作战对抗胜负结果。

1.2 无人集群防御作战效能

无人集群的防御作战效能可通过目标函数进行描述，该函数可同时用于遗传算法兵力部署优化。为方便描述武器装备类型，将5类装备分别用数字1～5代替，设单件装备可有效防御战区的概率为，则第′类单件装备有效防御第个战斗区域的概率′的计算方法如(2)式所示：

(2)

式中：(′)为第′类单件装备的总战斗效能指数；()表示第类武器的总数；()为第类武器所有装备的总战斗效能指数。第类多件装备有效防御第个战斗区域的概率′计算方法如(3)式所示：

(3)

式中：(′)表示在第个战斗区域中第′类武器数量占第类武器总数量()的比例，其约束条件为

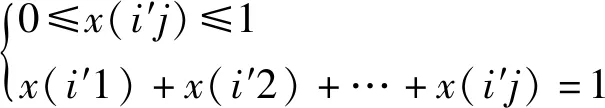
(4)

′的数学期望如(5)式所示：

(5)

根据上述分析，无人集群防御作战的目标函数构建为

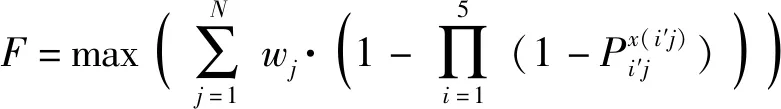
(6)

构建好的目标函数将用于进行无人集群的兵力部署，通过遗传算法对其进行优化，得出兵力部署方案。

2 无人集群兵力部署方法

根据无人集群的兵力部署问题设计遗传算法的优化过程。传统遗传算法容易出现过早收敛而陷入局部最优的情况，为避免出现此类问题，本文提出一种自适应遗传算法，对目标函数、交叉率及变异率3个方面进行优化。

2.1 算法参数设定

定义一个防御作战实例，对无人集群装备进行兵力部署。无人集群的装备种类和数量见表1。防御作战战场设有3个战斗区域，其中一个主要战斗区域、两个次要战斗区域，每个区域分别包含4、3、2个防御重点，战斗区域分布示意如图2所示。

图2 战斗区域分布示意图Fig.2 Battle area distribution diagram

设主要战斗区域的战斗强度因数为1，两个次要战斗区域的战斗强度因数分别为08和07。根据(1)式和(2)式分别计算作战重要程度因数及有效防御概率′，具体数值如表2所示，保留小数点后3位。

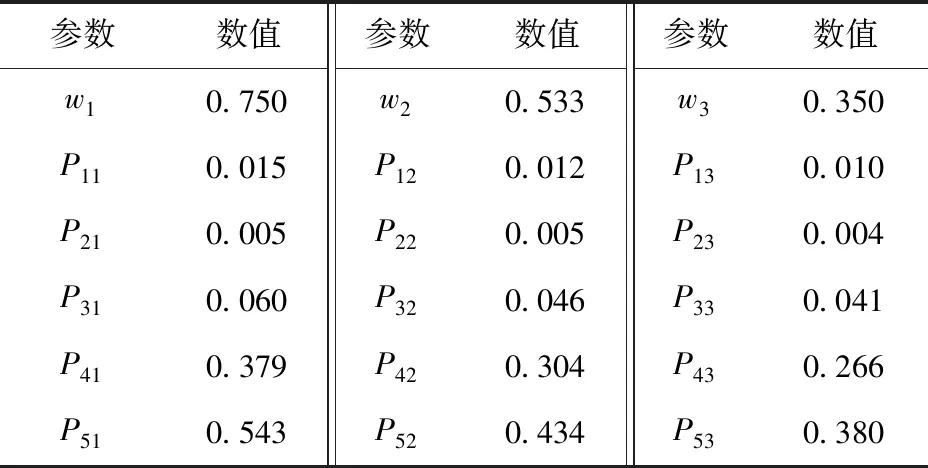
表2 两类参数数值Tab.2 Two types of parameter values

根据无人集群防御作战的任务和目标函数的设置，遗传算法的个体数目为40、最大遗传代数为200、变量维数为15、其上下界为[0，1]。为改变算法的局部搜索能力，使用格雷码进行编码，编码位数为20。适应度值分配采用线性排序方式，按照排序适应度因数进行排序。其排序适应度因数的计算方式如(7)式所示：

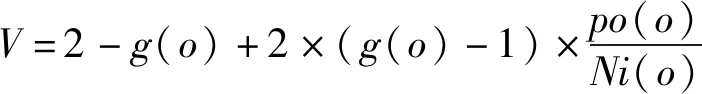
(7)

式中：()为种群中的待计算个体；()为排序种群的位置；()为种群中的个体数量。

2.2 算法改进

标准遗传算法在运行过程中，种群中个体的适应度值将逐渐趋于相似数值，难以继续优化，造成在算法过早收敛而未能找到最优解。为解决此类问题，本文对遗传函数的目标函数进行优化，优化后目标函数如(8)式所示：

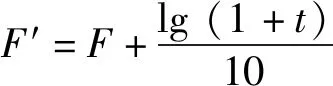
(8)

式中：为遗传算法的代数。随着算法的运行，对目标函数进行一个适当补偿，以提高高适应度的优势个体被遗传的概率，达到算法自适应的调整的目的。

在个体进行交叉和变异的过程中，若采用固定概率，则优秀个体和不良个体的交叉、变异可能性相同，不利于优秀个体的遗传。因此对算法的交叉及变异率进行改进，交叉率的计算方法如(9)式所示：

(9)

式中：为当前个体的适应度；为当前群体最大适应度；为每一代的平均适应度。变异率的计算方式如(10)式所示：

=01×

(10)

对交叉和变异率的改进能够使群体中具有较高适应度个体的交叉及变异率较小，更容易遗传给子代，适应度较群体较低的个体将更容易被进化。通过以上改进，遗传算法能够自适应地进行无人集群兵力部署的优化。

2.3 算法流程

根据21节及22节的算法设定，自适应遗传算法的运行流程如图3所示。

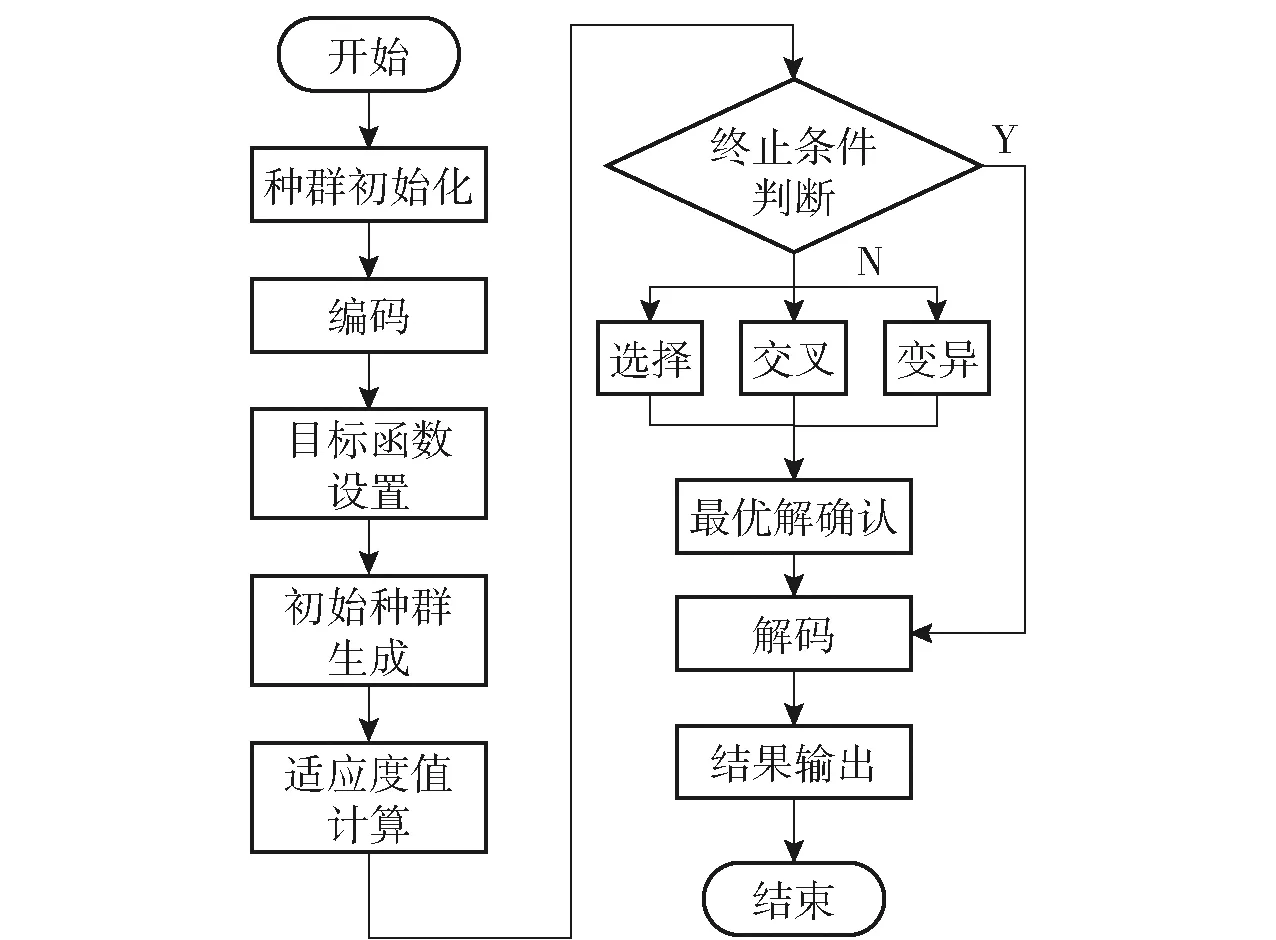
图3 自适应遗传算法运行流程图Fig.3 Fflow chart of adaptive genetic algorithm

首先根据算法参数设置进行种群初始化，随后按照格雷码进行编码，计算适应度值，在算法未终止之前，一直循环选择、交叉、变异及最优解的计算，待满足终止条件后，进行解码及结果输出。算法的终止条件设置为最大遗传代数，当达到该代数时停止计算。算法的伪代码如表3所示。

表3 自适应遗传算法伪代码Tab.3 Pseudo code of adaptive genetic algorithm

2.4 无人集群兵力部署结果

为与标准遗传算法进行对比，将标准遗传算法的变异率及交叉率设置为0.03和0.7。进行100次重复实验，取其平均值。标准遗传算法的平均最佳适应度曲线如图4所示。

图4 标准遗传算法平均最佳适应度曲线Fig.4 Average optimal adaptive curve of standard genetic algorithm

由图4可见，遗传算法的代数运行到40代时适应度值变化不再明显，进化过程受到阻碍，由此造成算法得到局部最优的结果。本文提出的自适应遗传算法平均最佳适应度曲线如图5所示。

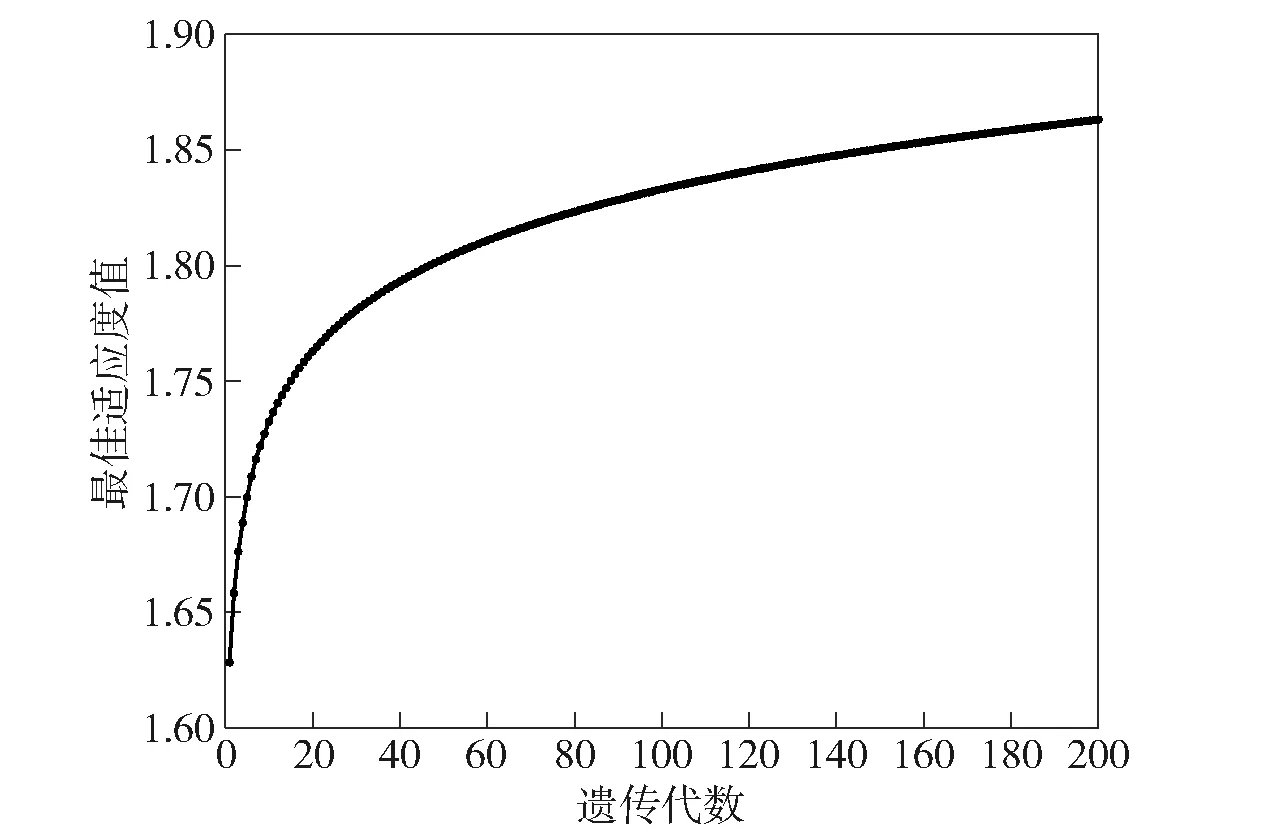
图5 自适应遗传算法平均最佳适应度曲线Fig.5 Average optimal adaptive curve of adaptive genetic algorithm

在增加了自适应参数调整后，适应度曲线呈现缓慢上升趋势，保证了更高适应度的优秀个体遗传，防止过早收敛及局部最优情况的出现。

对算法的100次重复实验进行平均，得到的()值及其对应的无人装备武器数量如表4所示。

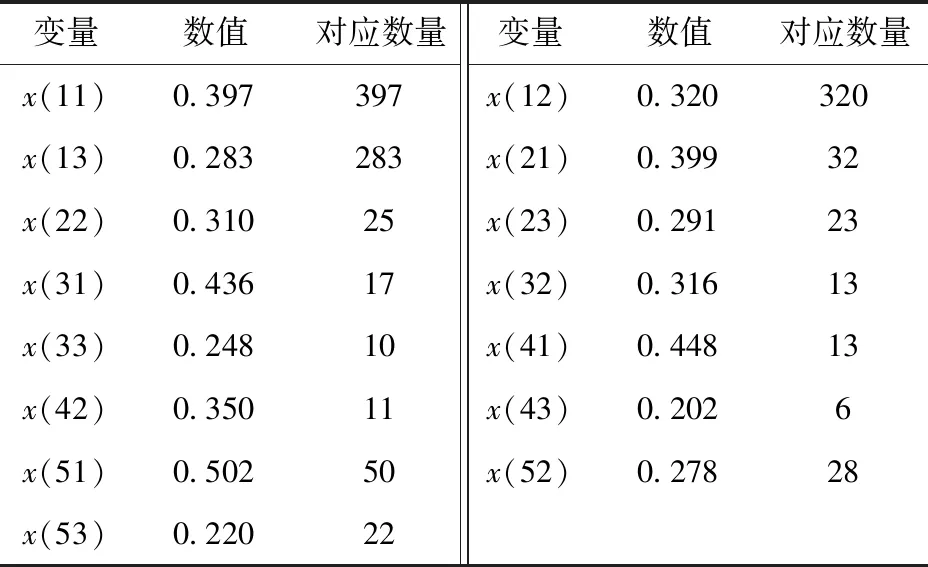
表4 算法运行结果Tab.4 Algorithm operation results

经过自适应遗传算法的优化，得到最佳的无人集群兵力部署方案为：在第1战斗区域分别部署各类无人集群装备397、32、17、13、50件；第2战斗区域分别部署各类无人集群装备320、25、13、11、28件；第3战斗区域分别部署各类无人集群装备283、23、10、6、22件。

3 无人集群协同任务分配方法

为进一步检验无人集群防御作战的兵力部署方案，本文提出一种改进的深度Q网络(DQN)深度强化学习算法，对无人集群任务分配进行优化，利用算法给出的方案进行防御作战，最终得到无人集群防御作战结果。

3.1 防御作战任务描述

防御作战任务即为防御方一定数量的无人集群装备Agent与攻击方一定数量的作战装备Agent进行作战。每轮对战在本模型中，攻击方采用和防御方一样的兵力构成，同样包含5种无人集群装备。分三波依次攻击3个战斗区域，若每波还有兵力剩余，则并入下一波进行攻击。双方作战流程按照OODA环进行循环战斗，直到一方Agent数量为0。基于OODA环的战斗按照侦察(Observation)、判断(Orientation)、决策(Decision)和行动(Action)4部分依次进行。本模型的观察部分即观测对方现有Agent的数量及种类，判断部分和决策部分则为无人集群任务分配部分，由深度强化学习算法完成，行动部分则按照任务分配方案进行作战。其作战流程如图6所示。

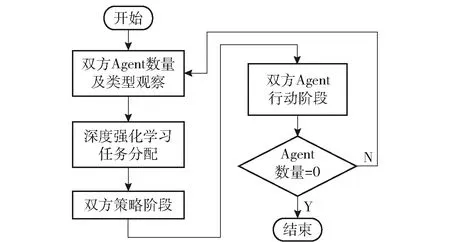
图6 无人集群防御作战流程Fig.6 Flow chart of unmanned swarm defensive combat

Agent的属性为={,}，其中为Agent的数量、为Agent战斗效能指数，=，在11节中定义。

任务的属性包括任务数量、任务优先级、任务执行质量及任务收益。任务数量为攻击方Agent个数，在防御作战的过程中，任务数量将实时变化，取决于当前进攻方还能有效作战的Agent数量。任务优先级与每类Agent的有关，越高则优先级越高。任务执行质量为Agent在攻击对方时是否能成功的概率，其计算方式如(11)式所示：

=1-(1-)()

(11)

任务收益函数与任务执行质量及Agent的战斗效能指数相关，对分配给Agent的任务进行价值衡量，其计算方法如(12)式所示：

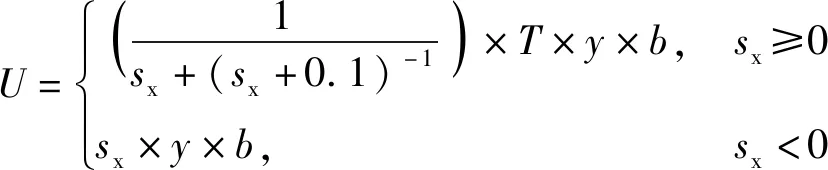
(12)

式中：为当前行动方与选定任务方的之差；为当前Agent是否参与任务的标志因数，当参与任务时=1，不参与任务则=0。

攻击方的策略原则为：任意选择小于等于自己的Agent进行攻击。防御方的策略由任务分配算法得到。只有不小于对方时才有可能成功攻击对方，成功攻击的概率由(11)式进行判定，否则攻击无效。

3.2 算法设置

DQN算法是包含预测网络和目标网络两个神经网络的强化学习结构，两个网络分别用于动作选择和动作执行后的奖励更新。网络的损失函数根据Q-learning构建。Q-learning的Q值更新方法如(13)式所示：

(,)=(,)+(+max(′,′)-(,))

(13)

式中：为状态；为动作；′与′为下一时刻的状态和动作；为学习率，∈[0,1]；为随机数；为折扣因数。在DQN算法中，网络的权重参数为，因此使用(,,)代替动作值函数(,)。传统DQN算法中，神经网络在计算Q值时容易出现过度估计问题，造成Q值高于实际值，使算法无法收敛至最佳状态。为解决上述问题，本文提出一种自适应权重Q值更新方法。其计算方式如(14)式所示：

(,,)=(,,)+(+
(max(′,′,)+
max(′,′,))-(1-)(,,))

(14)

式中：(，，)为更新后的Q值；为自适应调节权重因子，∈[0,1]，

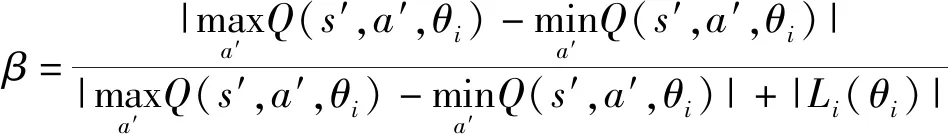
(15)

()为损失函数，

()=E[(+max(′,′,)-
(,,))]

(16)

根据(16)式，网络参数的梯度计算方式为

(17)

算法的目标函数采用随机梯度下降法进行优化。改进的自适应权重Q值更新方法可根据损失函数进行自适应调整，当=0为原DQN算法。策略选择使用贪婪策略进行策略更新，策略原理如图7所示。

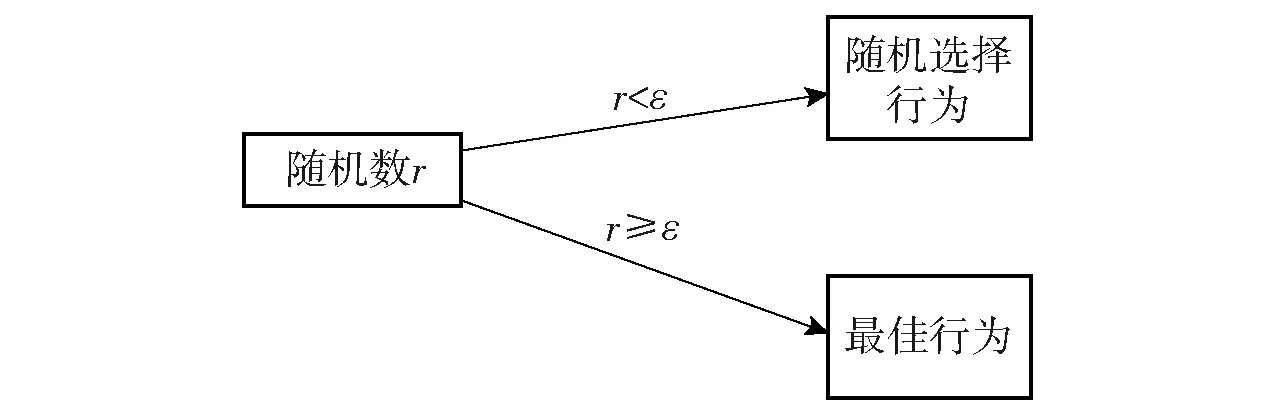
图7 ε贪婪策略原理Fig.7 ε greedy strategy principle

策略在非零概率的规则下进行选择，在概率为时随机选择行为，在概率为1-时根据网络权重选择当前最佳Q值对应的行为。

算法的回报计算方法如(18)式所示：

(18)

式中：、表示所有进攻方和防御方的总战斗效能指数；和为一轮攻击后当前进攻方和防御方剩余的总战斗效能指数。

算法的行为集合为防御方可能会选择进攻方的5类无人集群装备中的某一类，即={,,,,}，状态空间为防御方的五类无人集群装备，={,,,,}。设计深度强化学习算法神经网络结构如图8所示，输入层为防御方当前状态空间，输出为对应的任务分配动作Q值。

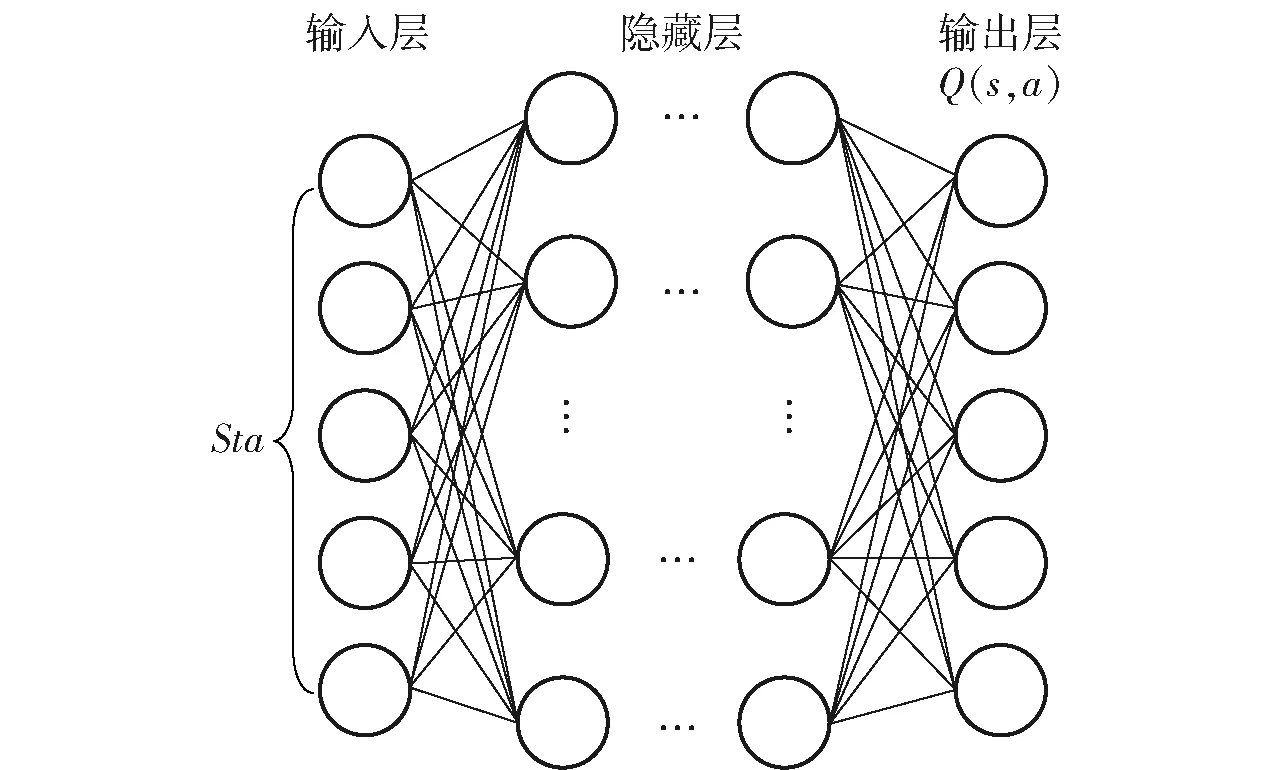
图8 算法神经网络结构Fig.8 Neural network structure of algorithm

3.3 算法流程

本文提出的深度强化学习算法流程如图9所示。

图9 深度强化学习算法流程Fig.9 Flow chart of deep reinforcement learning algorithm

首先构建经验池，用于存放算法产生的各类样本及数据，对其进行初始化，方便后续进行经验回放。随后对预测网络及目标网络权重、强化学习所需的参数、模型状态集合以及行动集合进行初始化。初始化完成后开始算法迭代。通过贪婪策略对动作进行选择，根据规则可随机选择或通过网络选择Q值最大的动作。其次根据动作执行及环境反馈得到奖励，获得新状态，将各类参数存入经验池。随机取出少量经验用于目标网络更新Q值，并通过梯度下降法更新权重。在迭代过程中使用预测网络的参数更新目标网络的参数。算法的伪代码如表5所示。

表5 深度强化学习算法伪代码Tab.5 Pseudo code of deep reinforcement learning algorithm

3.4 无人集群任务分配及防御作战结果

3.4.1 无人集群任务分配算法结果

模型采用2层全连接神经网络结构，每层神经元数量为(40，40)，训练10 000个回合，每个回合为一个episode，代表一次完整的任务分配和防御作战过程。重复实验100次。模型仿真参数如表6所示。

表6 模型参数Tab.6 Model parameters

按照遗传算法给出的最优无人集群部署方案进行部署：第1战斗区域分别部署各类无人集群装备397、32、17、13、50件；第2战斗区域分别部署各类无人集群装备320、25、13、11、28件；第3战斗区域分别部署各类无人集群装备283、23、10、6、22件。

进攻和防御均采取该方案，经过仿真实验，Q值在各种状态下均能收敛。防御方第1类无人集群装备的Q值误差如图10所示。

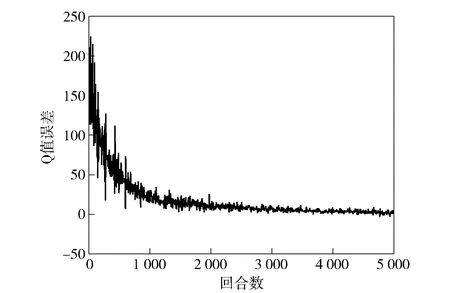
图10 防御方第1类无人集群装备Q值误差Fig.10 Q value error of the first class unmanned swarm equipment of the defensive side

Q值在最初几回合较大的误差波动后，随着回合数的增加逐步趋向于稳定。其中，防御方第1类无人集群装备的深度强化学习奖励曲线如图11所示。为进一步清晰观察奖励曲线的变化，在图11中添加强力曲线在1～200回合的局部放大图。从中可见，随着回合数的增长，初期奖励曲线迅速增加，随后呈现出趋势较微弱的缓慢增长。

图11 防御方第1类无人集群装备奖励曲线Fig.11 Reward value curve of the first class unmanned swarm equipment of the defensive side

3.4.2 防御作战结果

通过防御作战对无人集群的兵力部署算法进行效果验证，进攻方采用最优部署方案，且与防御方装备数量相等。防御方采用本文算法与标准遗传算法两种方式进行兵力部署，并分别利用本文提出的深度强化学习算法进行防御作战，对比作战成功率。对手的全部无人集群装备被损毁即为作战成功，损毁标准根据(11)式得到。作战成功率由100次重复试验的平均值得来，使用横坐标对应的训练回合数得到的任务分配结果进行作战。标准遗传算法的变异率及交叉率分别设置为0.03和0.7。本文提出的自适应算法根据数据适应度自行调整，结果如图12所示。

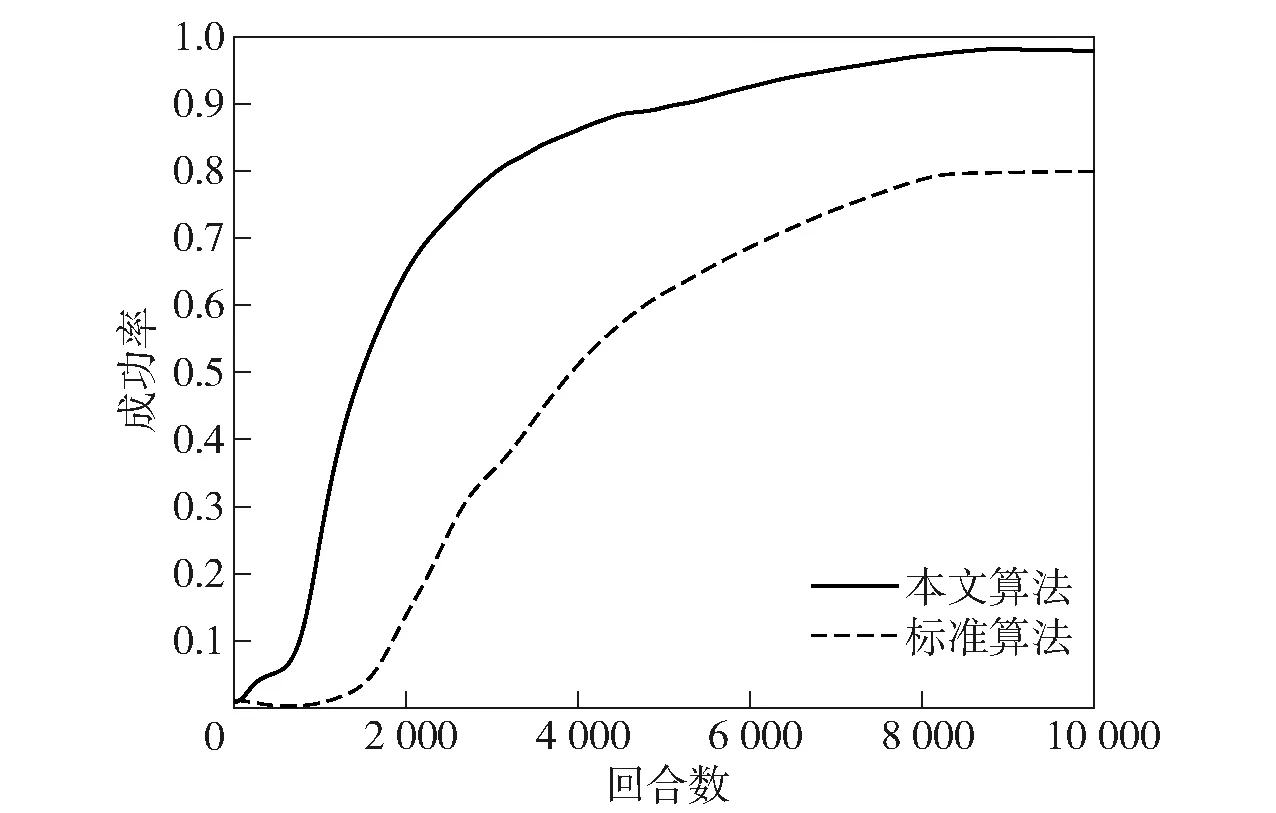
图12 采用不同遗传算法计算兵力部署方案的防御作战效果对比Fig.12 Comparison of the force deployment effects of different genetic algorithms in defensive combat

根据仿真结果，本文提出的无人集群兵力部署算法可增加无人集群防御作战的成功率，较标准算法可提高23%。同时，本文还使用其他文献提出的拍卖算法、粒子群优化算法及蚁群算法进行兵力部署，并将部署方案用于无人集群防御作战，将防御作战成功率与本文算法进行对比，算法对比结果如表7所示。

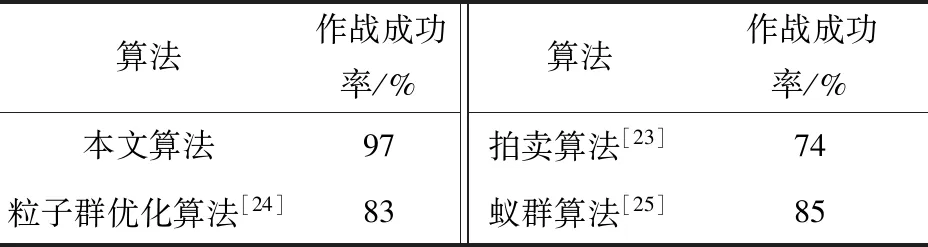
表7 算法对比结果Tab.7 Algorithm comparison results

对比结果表明，本文算法得出的兵力部署方案在进行无人集群防御作战时的成功率最高，蚁群算法与粒子群优化算法效果相近，拍卖算法次之，但均低于本文算法。本文算法能够更好地结合无人集群防御作战战场及武器装备的特点，利用有限兵力设计最优兵力部署方案，同时提高防御作战的成功率。

其次，对本文提出的无人集群任务分配算法效果进行验证，进行攻防双方防御作战。双方均采用自适应遗传算法得到的最佳装备部署方案进行作战，且数量相等。对比本文提出的深度强化学习算法与标准强化学习算法的防御作战效果，其结果如图13所示，取100次实验平均值。

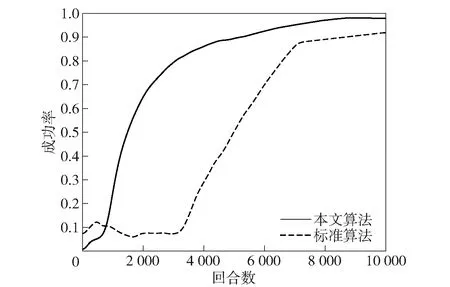
图13 深度强化学习算法防御作战效果对比图Fig.13 Comprison of defense combat effects of deep reinforcement learning algorithm

图13显示，标准强化学习算法因未对Q值进行过度估计修正，前期出现一定的波动，后续慢慢趋于稳定，但总体效果仍低于改进后的算法。本文提出的深度强化学习算法能够提高无人集群防御作战的成功率，提高效果为7%。

3.4.3 不同兵力下的防御作战结果

通过对无人集群兵力部署算法和任务分配算法的防御作战验证，均对防御作战的效果进行了提升，证明了本文算法的有效性。为进一步对模型的防御作战能力进行测试，对进攻方兵力数量的变化进行研究。在进攻方与防御方均为最优兵力部署的情况下，将进攻方兵力设置为多于防御方兵力0%、10%、20%及30% 4种情况，分别进行防御作战防真，成功率计算方法与前述方法相同，取100次实验平均值，仿真结果如图14所示。图14表明，在进攻方与我方兵力相同时，因我方采用基于深度强化学习的任务分配方式，防御作战成功率接近100%，随着进攻方兵力的逐步增加，防御方的作战成功率逐步下降，当进攻方兵力比我方多30%时，防御方已经不能成功防御，需要对防御方兵力进行提升。

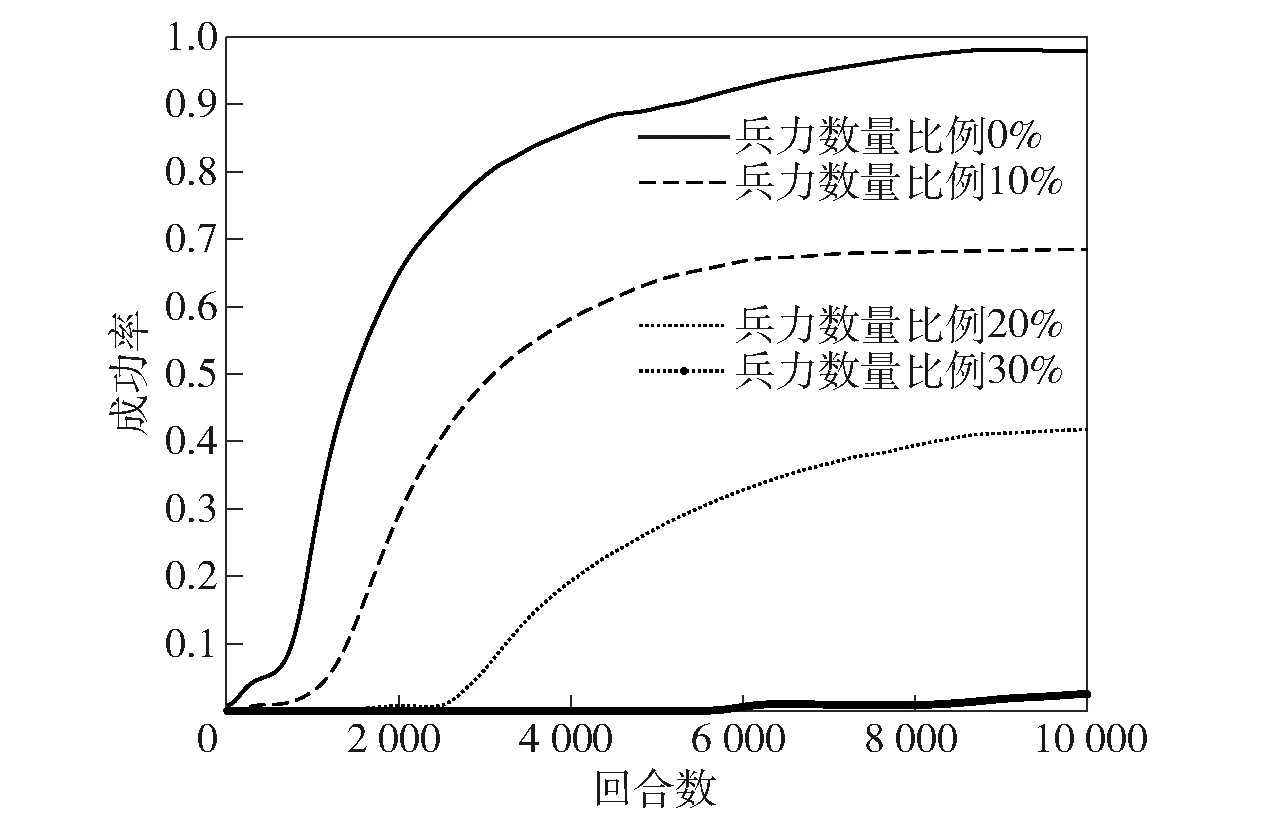
图14 多种进攻方兵力防御作战结果Fig.14 Defensive combat results of a variety of offensive-side forces

模型还对不同的兵力部署方案进行测试，防御方兵力部署方案除了2.2节和2.3节中提到的自适应遗传算法最优兵力部署方案，还分别采取兵力平均部署及随机部署方案。使用两种不同的兵力部署方法，由深度学习算法进行任务分配及防御作战仿真。其中，平均部署方案的仿真结果如图15所示，取100次实验平均值。图15的结果显示，当双方兵力相同时，最终能取得72.7%的作战成功率，进攻方兵力比防御方多10%时，虽然成功率只有45%，但并非不能防御作战。在进攻方兵力比防御方多20%时，防御作战不能成功。

图15 平均兵力部署方案防御作战结果Fig.15 Defensive combat results of average force deployment plan

最后，防御方采用随机部署方案，使用深度强化学习进行任务分配及防御作战效果如图16所示，取100次实验平均值。由图16可见，当防御方采用随机兵力部署方案时，在双方兵力相同的状态下，其成功防御的作战成功率仅为56%，即有将近一半的可能性会防御失败。在进攻方兵力比我方多10%时，已经几乎不能防御成功。

图16 随机兵力部署方案防御作战结果Fig.16 Defensive combat results of random force deployment plan

将上述3种不同兵力部署方案的防御作战效果进行汇总，结果如表8所示。

表8 多种兵力部署方案防御作战结果Tab.8 Defensive combat results of a variety of force deployment plans

由最优部署、平均兵力部署及随机兵力部署进行防御作战仿真的结果可知：最优兵力部署方案的防御作战效果最为显著，平均兵力部署方案次之，随机兵力部署方案最差。在进攻方兵力数量多于防御方数量时，最优部署方案在进攻方兵力多20%时，还具有42%的防御成功率；其他两个方案，在进攻方兵力多于20%及10%时已经几乎丧失防御能力。仿真实验结果也进一步表明，在防御方兵力有限的情况下，对进攻方的防御能力在兵力多于30%时达到极限，需要采用除兵力规划及任务分配之外的优化方案进行优化，如采用增援力量、提高自身防御兵力数等。

4 结论

本文构建了基于多智能体技术的无人集群防御作战模型，提出了一种无人集群兵力部署自适应遗传算法以及一种基于DQN的无人集群任务分配算法，对部署好的无人集群进行了任务分配和防御作战。得出主要结论如下：

1)本文提出的模型及算法可对无人集群防御作战的兵力部署及任务分配进行优化，优化后的防御作战成功率的提高率分别为23%和7%。

2)模型还研究了最优兵力部署方案、平均兵力部署方案及随机兵力部署方案3种方案下进攻方不同兵力的防御作战效果。其中，经过优化的最优兵力部署方案取得了最优的防御作战效果，防御作战成功率最高可达97%。

3)对部署好的无人集群进行任务分配和防御作战。结果表明，该无人集群兵力部署与任务分配技术可有效提高防御作战的成功率。