精密对称驱动二级微动放大系统设计及性能
杨满芝,景钢,郭卫,张传伟,武宏璋,魏凯洋,李林岳,吕振阳,桂皓晨,张晓栋
(1.西安科技大学 机械工程学院,陕西 西安 710054;2.西安计量技术研究院,陕西 西安 710082)
0 引言
近年来,超精密、高精度定位技术在军事工业领域得到了越来越广泛的应用,如何将输入位移进行精密的传动或转换,已经成为高精度机械系统研究的焦点。柔性铰链具有无摩擦、无迟滞、高精度等优点,可实现位移的精确导向、传动、转换等功能。基于柔性铰链技术设计的微位移放大机构可以对输出位移进行精确放大,满足实际应用中的工作行程要求[1-4]。基于柔性铰链设计微位移放大机构原理主要包括三角形原理(或平行四边形原理)、杠杆原理、压杆原理和其他放大原理[5-8],其中杠杆机构外形设计及工作原理简单、刚度小、放大比高、易于加工,调整微动机构的结构便可获得不同的放大比。在杠杆放大微动机构中,由于其非运动方向受力会产生一定的寄生运动,使机构产生非运动方向力和位移,导致机构运动精度下降,并影响机构运动时的安全性。因此进行微动机构消除寄生运动研究具有重要意义。
张群明[9]设计了单级杠杆放大机构,用于夹持微小器件,可实现微小位移的精准放大,完成微装配的各种作业任务。Ma等[10]设计了一种适用于非圆车削的新型单自由度柔性铰链机构来放大压电致动器的输出位移,对结构的静、动力特性进行了理论分析,建立了结构的微分方程,并用有限元方法进行了验证。Hwang等[11]在考虑杠杆弯曲变形的情况下,推导出具有杠杆柔性铰链一级放大机构精密定位平台的位移放大比公式。然而一级微动放大机构存在放大比有限的缺点,无法满足一些较大的运动位移需求。二级微动放大机构可解决运动比放大有限的问题。Liu等[12]基于柔性铰链结构设计了一种新型大行程微夹持器,采用二级柔性放大器的机构设计实现了压电驱动器的行程放大,在非工作方向的位移极小,可应用于各种微装配场合。沈剑英等[13]基于杠杆式二级放大柔性铰链机构,在考虑铰链转动中心偏移量的基础上,对放大机构的放大比计算公式进行了推导。卢倩等[14]提出了一种二级放大机构设计方案,该机构采用直圆型柔性杠杆放大原理并进行了结构优化,其放大率及运动精度大幅度提高。但是,现有研究的二级杠杆放大机构在运动时存在寄生位移,导致运动不精确并影响其安全性。
为解决微动机构放大比有限且有寄生运动的问题,本文基于直圆型柔性铰链的导向、传动作用及杠杠放大原理,设计了一种无附加位移及力且放大比可调的对称驱动二级微动放大机构,利用压电陶瓷致动器作为微驱动器设计了微动系统,并对系统的强度、动态及运动性能进行了分析,分析显示系统具有运动精度高、安全性强、放大比大且可调等优点。本文研究成果可在精密加工与制造领域发挥作用。
1 二级微动放大系统设计
1.1 系统结构设计
设计的二级放大系统三维模型图如图1所示,x轴、y轴和z轴方向外形尺寸为138 mm×192 mm×50 mm,共包含32个直圆型柔性铰链,呈轴对称式分布,系统采用压电陶瓷致动器对微动机构进行驱动。
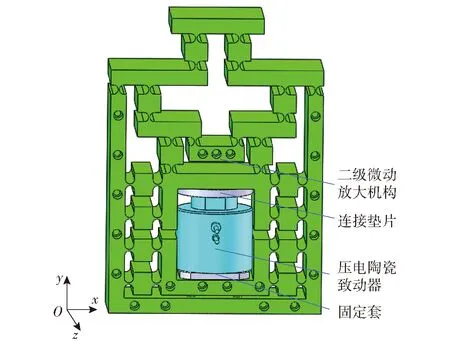
图1 二级放大系统三维模型Fig.1 3D model diagram of the two-stage amplification system
1.2 二级微动放大机构设计
1.2.1 柔性铰链
柔性铰链利用柔性材料在结构薄弱部位受力时产生微小变形来实现对运动和位移的精确传动,最终实现运动的精密导向、传动及转换。根据外形不同,柔性铰链可分为圆弧型、直圆型、抛物线型及直梁型等[15-17]。直圆型柔性铰链能满足运动范围及精度的要求,其转动精度较高、结构简单、易加工、应力小、运动性能稳定[18-20]。综合以上因素,本文选用转动精度较高的直圆型柔性铰链。
1.2.2 柔性铰链组件
柔性铰链组件由柔性铰链与其他构件连接而成。柔性铰链组件模型如图2所示。柔性铰链组件af由ab段、bd段及df段组成,其中ab段和df段为柔性铰链。假如组件af足够长,可以将其视为梁结构组件,当其在Oxy面内受到平行于y轴方向的载荷py时,梁af将产生x轴方向的拉压变形和Oxy面内的弯曲变形。梁af可视为由梁ab、bd和df刚性结合而成,其中,ab、df是直圆型柔性铰链,可等效为变截面梁模型,又可将其通过离散分解为众多等截面梁(离散份数N值越大,离散越精确)。
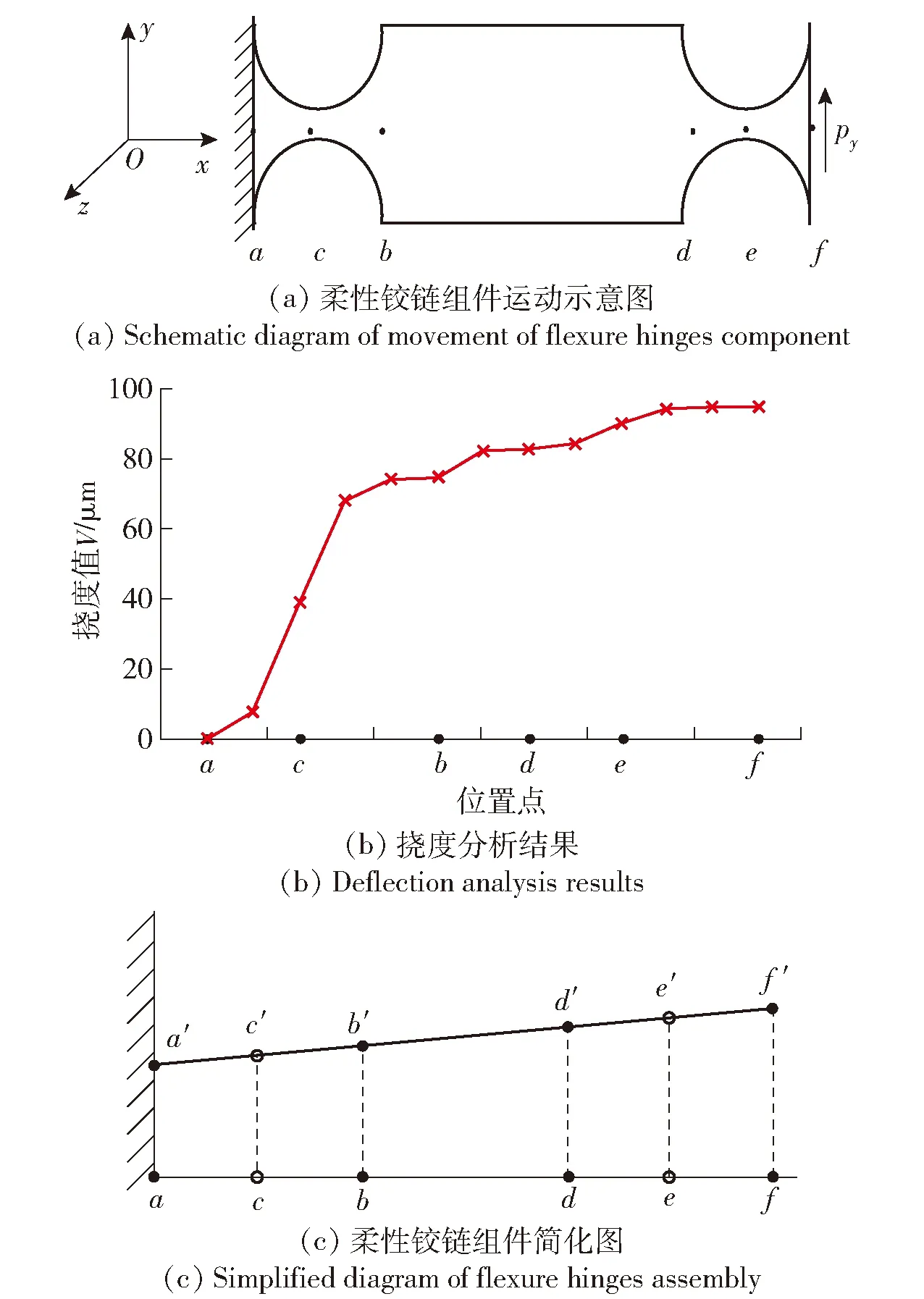
图2 柔性铰链组件模型Fig.2 Model of flexure hinges component
图2(a)情况下梁af的挠度分析结果如图2(b)所示。图2(b)中,点a、b、c、d、e、f为柔性铰链组件运动前的简化图,点a′、b′、c′、d′、e′、f′为柔性铰链组件运动后的简化图。由图2(b)可以看出,在柔性铰链的中心点c、e处挠度变化率很大,可以将柔性铰链的中心视为其转动中心。由于运动后梁af内部各点均产生挠度且点c、e为柔性铰链转动中心,可将图2(a)的柔性铰链组件运动前后简化为图2(c)。
1.2.3 微动机构设计
微动机构的工作原理如图3所示,其中各个柔性铰链编号为1~32。本文机构的驱动、导向具有对称性,故取其右半部分对其进行分析。当系统工作时,压电陶瓷致动器(PZT)沿着y轴正向产生输入位移yi,输入位移由柔性铰链16、14沿y轴正向传递至第1级杠杆机构;在第1级杠杆机构中,柔性铰链13为固定约束,柔性铰链14为输入位移,放大后的位移经由柔性铰链10沿y轴正向传出;柔性铰链10将位移沿y轴正向传递至柔性铰链7,进入第2级杠杆机构;在第2级杠杆机构中,柔性铰链8为固定约束,柔性铰链7为输入位移,放大后的位移经由柔性铰链4沿y轴正向传出;柔性铰链4将二级放大后的位移沿y轴正向传递至柔性铰链2,在机构顶部输出位移yo。本文机构中共有21个沉头孔,其中,柔性铰链5及8下方的10个孔用来固定机构;柔性铰链12及13下方的3个孔可为机构一级放大提供固定作用;柔性铰链30及31之间的4个孔用以固定机构以确保压电陶瓷驱动器驱动时系统只沿y轴正向运动;机构最下方4个孔用以固定机构并通过推力为压电陶瓷致动器工作时提供预紧。

图3 二级微动放大机构原理示意图Fig.3 Schematic diagram of two-stage micro-drive amplification mechanism
在系统运动过程中,柔性铰链17~32组成的8个柔性铰链组,可抵消在运动过程中产生的大小相等、方向相反的非运动方向(x轴)的力和位移。因此,在机构的运动过程中避免了非运动方向的力和位移,保证了压电陶瓷致动器的安全性、提高了运动精度。
1.3 微驱动器选型
PZT以驱动力大、体积小、动态特性好、位移分辨率和频响高且无噪声、无震动、不发热、换能效率高的优点,成为目前微位移驱动较为理想的驱动元件,在精密定位领域得到了越来越广泛的应用。
按照系统对微驱动器的外形及输出性能的要求,本文选用德国PI公司生产的P-235.1s型压电陶瓷致动器,压电陶瓷最大伸长量为15 μm,最大运动频率为300 Hz,其主要参数如表1所示。
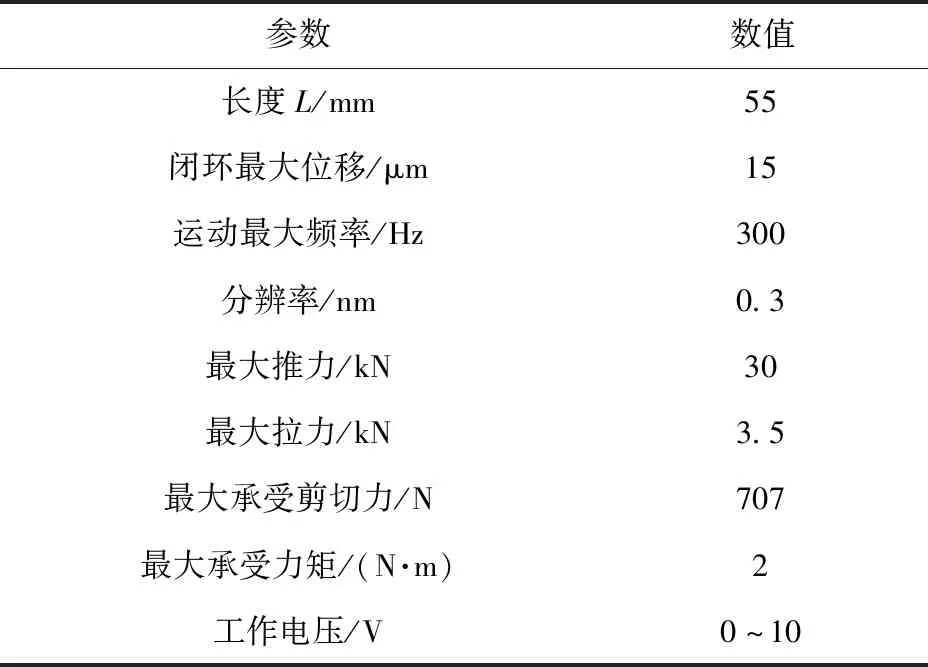
表1 压电陶瓷致动器(P-235.1s型)主要参数Tab.1 The main parameters of P-235.1s PZT
2 二级微动放大机构运动性能分析
2.1 微动机构对称驱动性能分析
在微动放大机构运动过程中,由于非运动方向受到力和位移通常会产生一定的寄生运动。微驱动器非运动方向的强度一般很差,产生的寄生运动易对微驱动器造成损坏,影响系统运动过程中的精密性和安全性。因此消除寄生运动对于微动机构具有重要意义。本文机构采用对称柔性铰链组结构,利用导向原理和附加力平衡原理,可有效消除寄生运动。
2.1.1 二级微动放大机构的导向原理分析
将图2所示的柔性铰链组件作为导向单元对称分布于微驱动元件的两侧,即可实现微动机构的导向作用,可视为直线运动导轨。导向单元的导向原理如图4所示,其中1为固定微动机构的工作台,2为移动件,4个导向单元3、4、5、6构成直线运动导轨对移动件2的直线运动导向。其中,图4(a)为导向单元组处于平衡状态的结构示意图,图4(b)为导向单元组运动后的结构示意图。此时,在驱动载荷作用下移动件2运动至2′位置。4个导向单元3、4、5、6分别运动至3′、4′、5′、6′位置。

图4 导向机构导向原理图Fig.4 Guiding mechanism guiding schematic diagram
以导向单元5为例对其导向原理进行分析,建立直角坐标系,如图5所示。导向单元由两个柔性铰链和连接杆I组成,将第1个柔性铰链简化为转动副c及杆ac、cb,将第2个柔性铰链简化为转动副e及杆de、ef。其中,设杆ac、cb、de、ef长为lj(j取值为ac、cb、de、ef),杆I长为lI。导向单元左端自由右端固定,运动前导向单元结构示意图如图5(a)所示,运动后导向单元结构示意图如图5(b)所示,y轴为微动机构的运动方向,柔性铰链组件在左端受力,在y轴方向产生Δu位移时,由于导向单元右端固定,导向单元将产生拉伸及弯曲变形,即等效为各杆的拉伸及铰点的转动。导向单元右端固定,左端移动Δu,可近似视为导向单元转动了Δθ。可将导向单元导向运动等效为图5(c),在左端受力移动Δu时组件将发生Δθ转动。
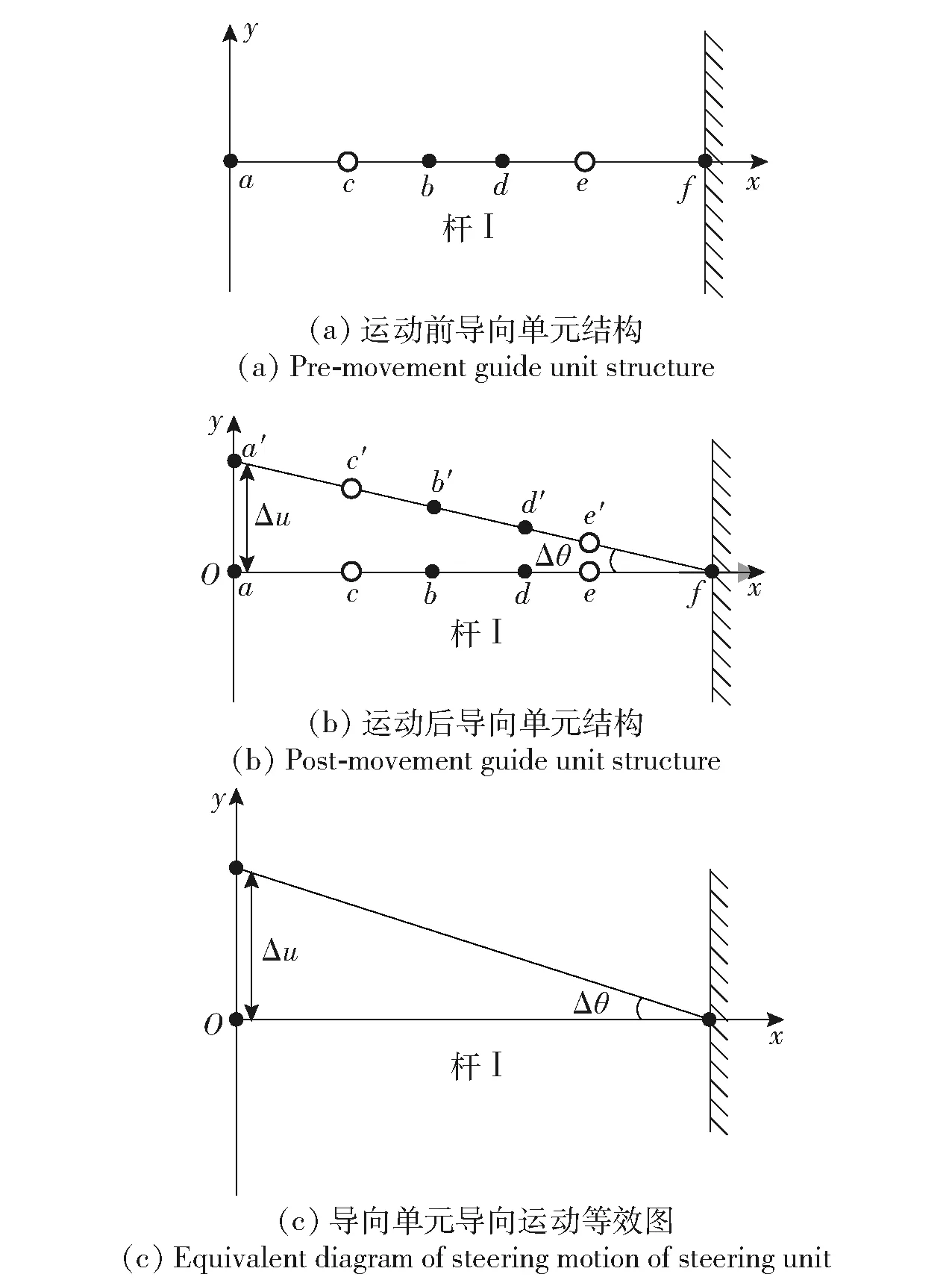
图5 导向单元导向工作原理示意图Fig.5 Schematic diagram of guiding principle of guiding unit
同理,可对图4中的导向单元3、4、6导向性能进行分析。由于4个导向单元3、4、5、6相对于固定台1及移动件2呈对称分布,实现了移动件相对于固定台1的运动导向,当移动件2运动Δu时,各个导向单元均转动了Δθ。
运动后导向单元总长l近似为
(1)
运动后导向单元与x轴夹角Δθ近似为
(2)
导向单元各个位置点运动后的y轴方向位移近似为
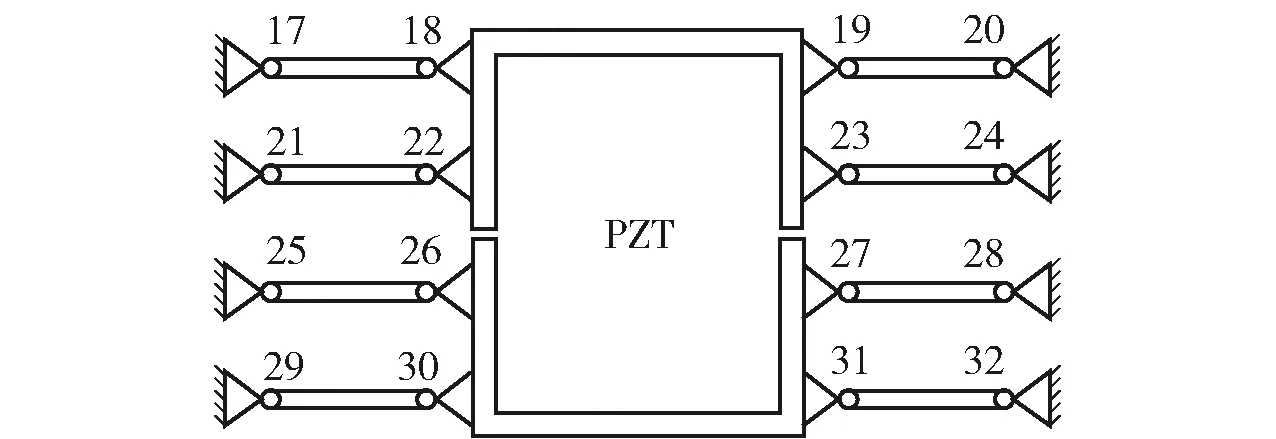
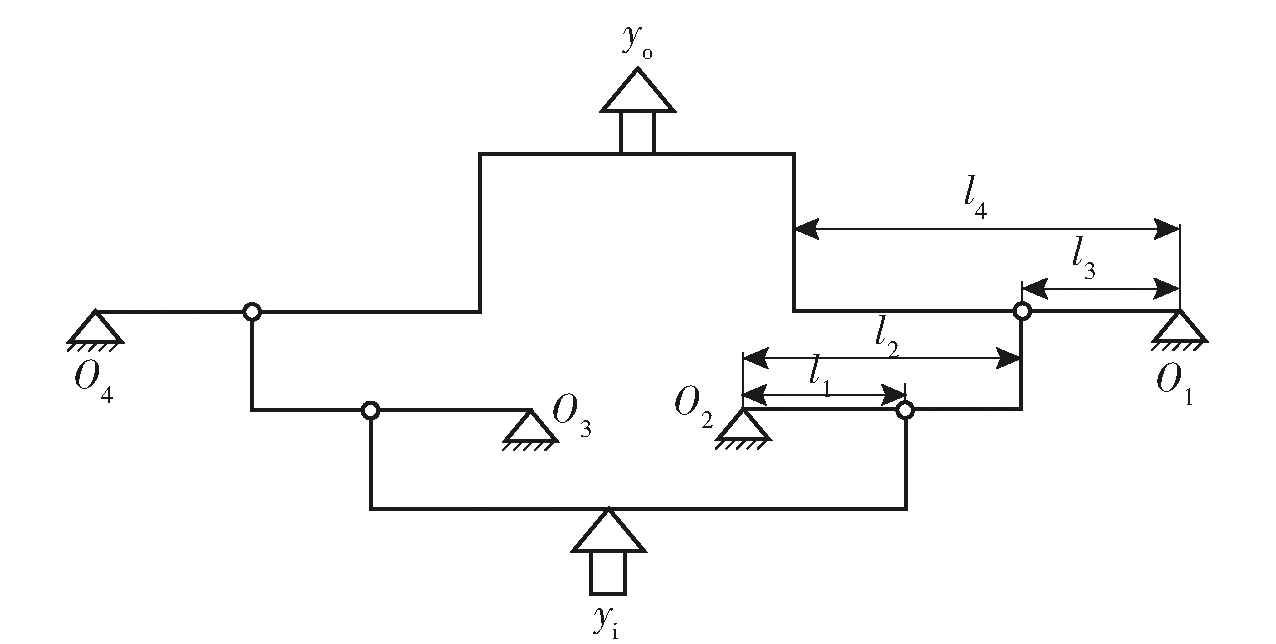
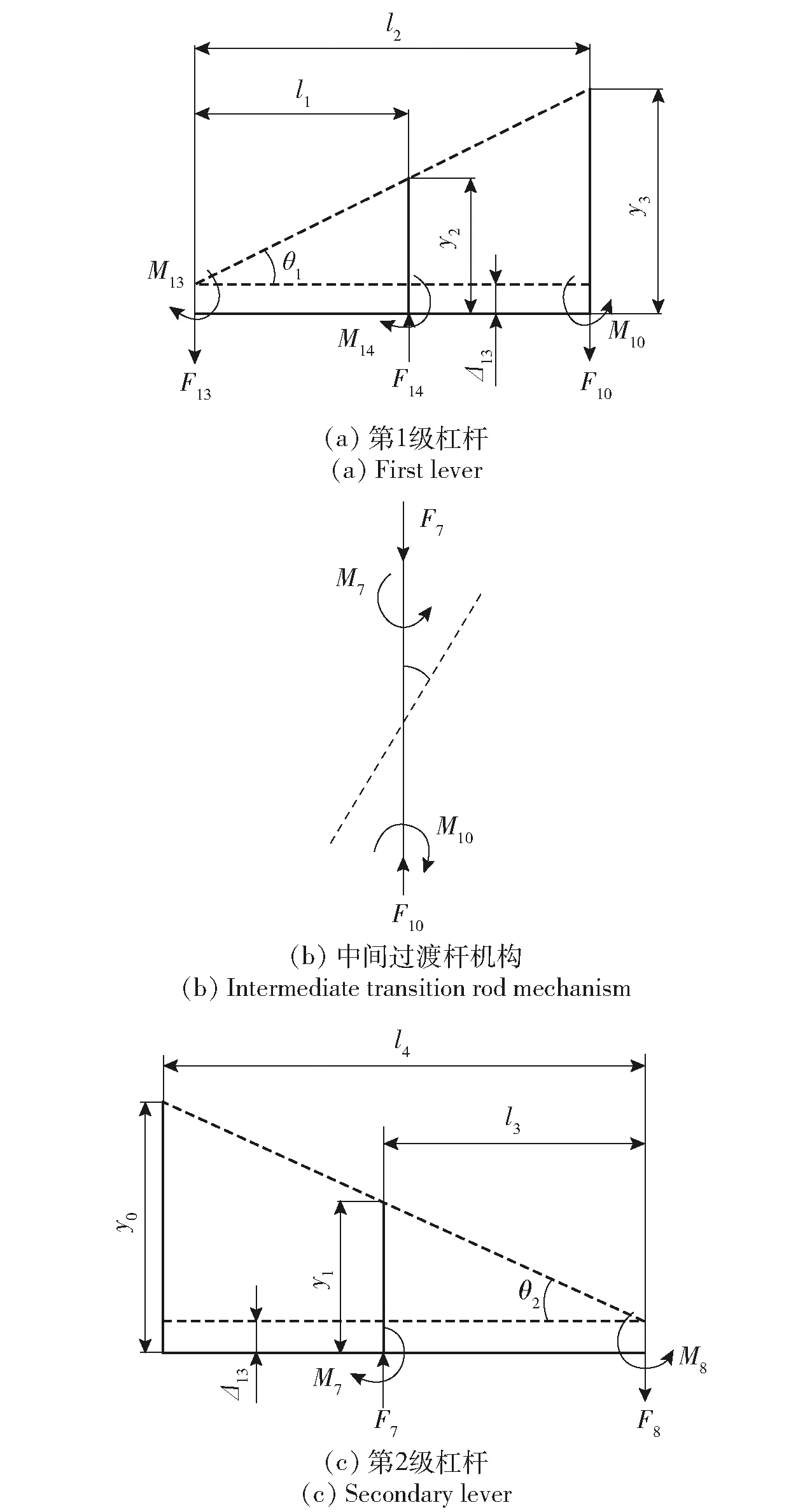
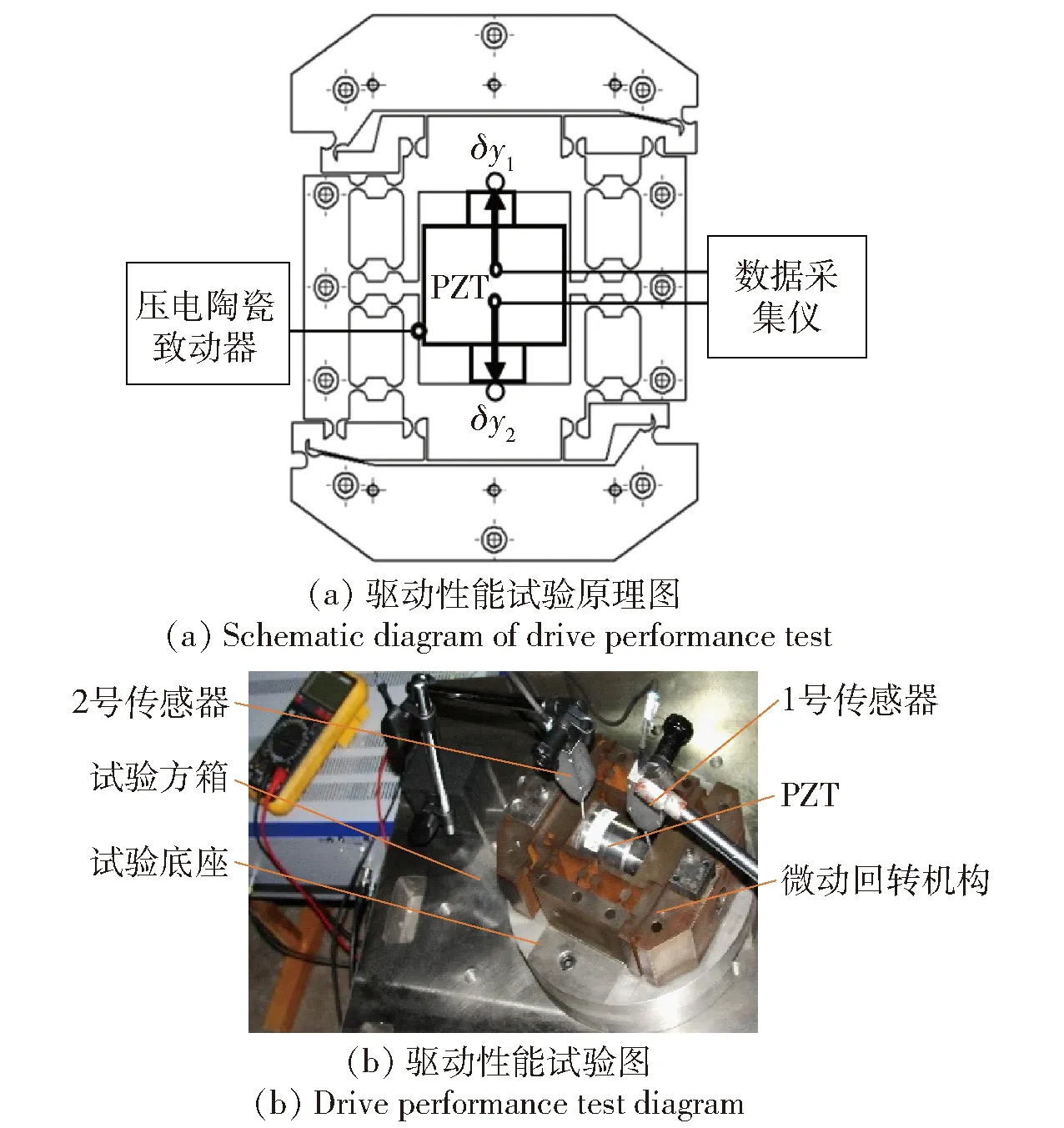
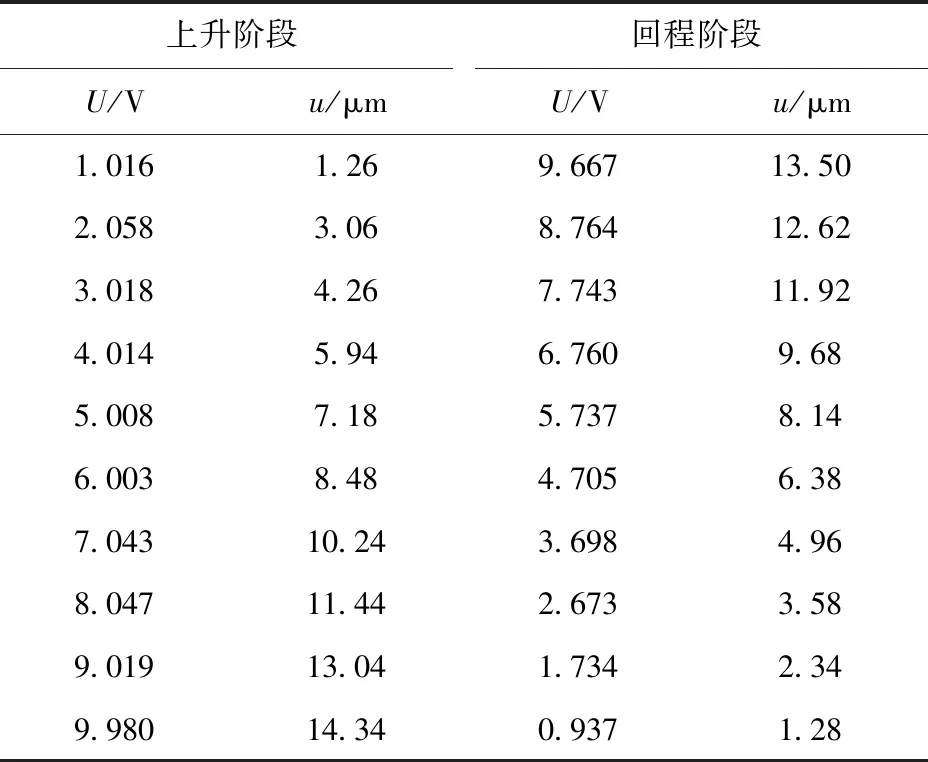
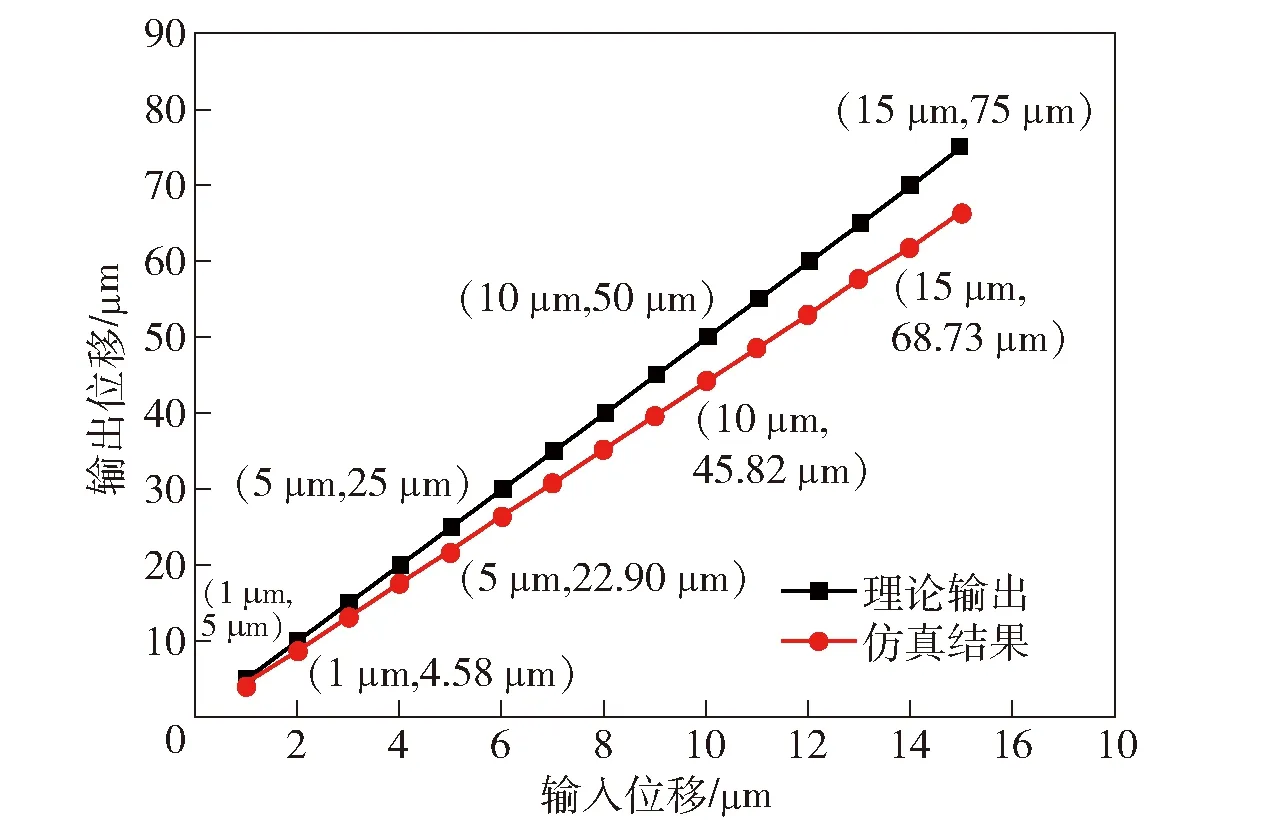
y′k=(lI+4lj-xk)tan(Δθ),0 (3) 式中:xk、y′k分别为各点x轴方向坐标值、运动后各点y轴方向位移值。(3)式即为导向单元导向运动数学模型。 在微动机构运动过程中,在运动方向y向机构有运动位移,由于4个导向单元3、4、5、6呈对称分布,运动过程中各杆伸长而产生的力或力矩被对称结构消除,从而保证机构只在运动方向有运动位移,在非运动方向无运动位移。 因此,当图4中的移动件2作直线运动时,可以通过导向单元产生的拉伸及弯曲变形完成对运动的导向,这就是二级放大微动机构的导向原理。故运动过程中不会产生附加位移,从而保证了机构运动过程中的精密性。 2.1.2 二级微动放大机构附加力平衡原理分析 为了直观形象,设计方案图中柔性铰链组件用铰点表示,例如图6(a)中柔性铰链组件acbdef用图6(b)的铰点c、e组成的组件ce表示。 图6 柔性铰链组件等效简化图Fig.6 Equivalent simplified diagram of flexure hinge components 二级微动放大机构附加力平衡原理如图7所示,中间空心位置处放置PZT,柔性铰链17~32分别组成8个柔性铰链组件,对称分布在驱动器两侧。在运动过程中,除会产生运动方向(y轴方向)的力外,还会产生非运动方向(x轴方向)的附加力,而压电陶瓷致动器在非运动方向脆性较大,受力易损坏,故设计关于y轴对称分布的8个柔性铰链组件来平衡非运动方向的附加力。 图7 二级微动放大机构附加力平衡工作原理图Fig.7 Working principle diagram of additional force balance of the two-stage micro-drive amplification mechanism 因此,在运动过程中产生的x轴方向附加力大小相同、方向相反,互相抵消,实现了微动机构附加力平衡,防止运动过程中横向附加力的存在,从而保证了压电陶瓷致动器在运动过程中的安全性。 二级放大系统三维模型图如图1所示,二级微动放大机构原理示意图如图3所示,对其分析得出微动机构的放大原理图如图8所示,因微动机构具有轴对称性,故取右半部分进行放大比分析。 图8 二级微动机构放大原理图Fig.8 Enlargement schematic diagram of two-stage micro mechanism 设计的对称驱动二级微动放大机构的放大比可根据实际需求进行调节,具体是调节微动机构中柔性铰链间杠杆的长度,即图8中l1~l4的长度。 取任意一组特定值进行分析计算,即l1=15 cm,l2=30 cm,l3=20 cm,l4=50 cm。在微动机构运动时,其放大比会因各柔性铰的挠度、拉伸及压缩等变形而发生变化。设柔性铰链i(i取值为1~32)的轴向力为Fi,力矩为Mi,柔性铰链i产生的轴向变形为Δi,转动角度为αi,则其变形量与所受力及力矩之间关系可表示为 Fi=KFΔi (4) Mi=KMαi (5) 式中:KF为柔性铰链的轴向拉压刚度, (6) E为机构材料的弹性模量,b为柔性铰链z轴方向宽度,s为柔性铰链的切口半径r与最小厚度t之比;KM为柔性铰链的转角刚度, (7) 设微动机构中第1级、第2级、中间过渡杠杆的转角分别为θ1、θ2、θ3,则柔性铰链的转角αi和杆件的转角θj之间存在如下关系: α13=α14=θ1 (8) α10=θ1+θ3 (9) α7=θ1-θ3 (10) α8=θ2 (11) 二级微动放大机构受力与位移关系分析如图9所示。其中,图9(a)为机构第1级杠杆的受力及位移放大情况,本级杠杆绕柔性铰链13的旋转中心转动,分析可得: 图9 二级微动放大机构受力与位移关系分析Fig.9 Analysis of force and displacement of the two-stage micro-drive amplification mechanism F14=F13+F10 (12) F10l2+M13+M14=F14l1+M10 (13) 设二级微动放大机构的输入位移为yi,作用在铰链14、16组成的柔性铰链组件轴向方向上,在轴向力作用下铰链14、16产生压缩,压缩位移为Δ14和Δ16;同时,铰链13的旋转中心会产生偏移,其偏移位移为Δ13,则第1级杠杆的输入位移量y2为 y2=yi-Δ14-Δ16 (14) 机构第1级放大的输出位移量y3为 y3=θ1l2+Δ13 (15) 第1级杠杆的转角θ1为 (16) 图9(b)为二级微动放大机构的中间过渡杆,即由柔性铰链7、10组成的柔性铰链组件的受力与位移分析图,分析可得: F7=F10 (17) M7=M10 (18) 图9(c)为机构第2级杠杆的受力与位移图,第2级杠杆绕柔性铰链8中心转动,则 F7=F8 (19) M7+F7l3=M8 (20) 在第1级杠杆的推力作用下,设柔性铰链7和10由于轴向受压产生的变形分别为Δ7和Δ10。由于过渡杆推力F7的作用,铰链8的中心会产生偏移,设其偏移量为Δ8,则机构第2级放大有效输入位移y4为 y4=y3-Δ7-Δ10 (21) 机构的第2级放大输出位移(机构的最终输出位移)yo为 yo=Δ8+l4θ2 (22) 第2级放大机构转角θ2为 (23) 联合(4)式~(23)式,得出二级微动放大机构放大比A的计算公式为 (24) 式中: p4=l1(6l1-12l2-19l3)+l3(9l3+34l2) 直圆型柔性铰链结构参数如下:铰链切口半径r=3 mm,最小厚度t=1 mm,l1=15,l2=30,l3=20,l4=50。铰链最小厚度t、切口半径r的数值根据相关文献及本课题组前期相关研究(如微动回转机构设计)的经验设计,它们的数值可以根据实际情况与需要改变(如压电陶瓷致动器的直径值变化),但是经本课题组相关研究表明它们的变化对系统的放大比及运动精度等性能影响较小且无规律性。 机构的材料选用60Si2Mn,材料弹性模量E=2.06×1011Pa。将相关参数代入(24)式,可得二级微动放大机构的放大比A=5.001 2≈5。 由分析计算的结果可以看出,本文设计的微动放大机构放大比较大,且可根据使用需要通过调整关键杆的长度调整放大比。 本文系统的微驱动器选用压电陶瓷致动器,其具有蠕变、迟滞、非线性等不足,这些特点与压电材料的性能如电致伸缩效应、压电与逆压电效应、铁电效应等有关。为了考察本文设计的微动系统的驱动性能,利用一种微动回转机构对P235.1s型压电陶瓷致动器进行驱动性能试验。 压电陶瓷致动器驱动性能试验如图10所示,其中原理图如图10(a)所示,试验图如图10(b)所示,利用试验方箱、压电陶瓷致动器、微动回转机构、试验底座、电感位移传感器(位移传感器为分辨率为0.05 μm的旁式电感位移传感器,试验所用传感器分别编号为1号传动器和2号传感器)等装置进行试验,试验方箱放置于隔振台上,底座固定于试验方箱上,微动回转机构装配压电陶瓷致动器后固定于底座上。压电陶瓷致动器的电压U由控制系统控制,y轴方向的1号与2号电感传感器位移变化值为δy1、δy2,则压电陶瓷致动器的伸长量u为 图10 压电陶瓷致动器驱动性能试验Fig.10 Driving performance test of PZT u=|δy1|+|δy2| (25) 分别对压电陶瓷致动器上升和回程运动性能进行测试,试验结果如表2所示。对试验结果进行线性拟合,结果如图11所示。 表2 压电陶瓷致动器驱动性能测试试验结果Tab.2 Driving performance test results of PZT 图11 压电陶瓷致动器运动性能线性拟合图Fig.11 Linear fitting diagram of the kinematic performance of PZT 将上升阶段压电陶瓷致动器的工作电压U与压电陶瓷致动器伸长量u拟合成线性方程为 u=1.444U-0.046 86 (26) 其线性度为 0.999 1;将回程阶段压电工作电压U与压电伸长量u拟合成线性方程为 u=1.444 1U-0.200 46 (27) 其线性度为0.996 7。 由试验结果及其线性拟合结果可以得出以下结论: 1)P-235.1s型压电陶瓷致动器上升和回程不一致且具有一定的非线性,但其误差很小。 2)由其运动线性拟合结果看,P-235.1s 型压电陶瓷致动器上升阶段与回程阶段线性度很高,表明系统的驱动性能优良。 为对系统的强度、模态、运动性能进行分析,采用有限元法对微动系统进行模拟仿真,在微动系统中,压电陶瓷致动器仅提供系统的输入位移,故只对微动机构进行分析即可。 在有限元软件中导入微动机构的结构模型立体图,并选择60Si2Mn材料参数对机构进行整体网格划分,模型共划分为366 048个单元,544 272个节点。 微动机构强度分析主要分析机构在运动时是否发生破坏,因此需要计算其在压电致动器最大驱动位移下的最大模拟应力。 分析在有限元静力学模块中进行,对机构上的21个螺栓孔施加固定约束,在驱动器的位置处施加y轴正向位移15 μm进行求解,得到的应力云图如图12所示,该机构最大模拟应力为108.59 MPa。 图12 应力云图Fig.12 Stress diagram 材料许用应力为 (28) 式中:σs为60Si2Mn屈服极限。将σs=1 176 MPa及设定安全系数λ=1.5代入(28)式中,计算出材料的许用应力σ为784 MPa。而通过有限元计算,机构的最大模拟应力仅为108.59 MPa,其值远小于材料许用应力值。 有限元分析结果显示,系统在运动过程中安全可靠,其微动机构最大应力符合材料强度要求。因此,系统强度符合设计要求,系统具有较好的强度性能。 为分析系统在运动过程中动态性能,需要进行微动机构的固有频率分析,以判断在运动过程中系统是否会产生共振现象。 采用有限元的modal模块对机构进行自由模态分析。有限元分析结果显示其前6阶固有频率值为316.55 Hz、454.22 Hz、663.62 Hz、719.08 Hz、1 252.2 Hz、2 316.8 Hz。 系统采用P-235.1s压电陶瓷致动器,其最大运动频率是300 Hz,而有限元仿真结果显示系统的第1阶固有频率为316.55 Hz,因此系统具有较好的动态性能且运动过程中不会发生共振。 采用有限元软件对二级微动放大机构进行有限元分析,计算其放大比。取机构的输入位移1~15 μm(即压电陶瓷致动器伸长量范围)作为分析的初始条件,计算系统的输出位移值,运动学分析结果如表3所示。 表3 微动机构运动学分析Tab.3 Kinematics analysis of micro mechanism 将输入值与理论输出值、仿真结果分别进行线性拟合,结果如图13所示。 图13 输入值与输出值的关系Fig.13 Relationship between inputvalues and output values 由运动学分析结果可知,系统在运动时误差为8.36%,理论放大比为1∶5,运动学分析放大比最大为1∶4.58,表明系统运动具有较高的精密性且定位精度可达到微米级。由于模型假设与实际有限元计算存在差别,有限元仿真的结果和理论计算的数值有一定的计算误差,但其误差较小(相对误差为8.36%),在可接受范围之内。 本文针对目前精密微动放大系统研究中放大比有限、存在寄生位移及非运动方向受力运动的问题,设计了一种由压电陶瓷致动器驱动二级微动放大机构的微动系统,并对微动系统的相关性能进行了研究。得出主要结论如下: 1)设计了一种精密的二级微动放大系统,该系统可根据实际需要调整放大比,同时该系统具有强度性能、动态性能及定位性能优良的特点(最大绝对误差为6.27 μm,相对误差为8.36%),克服了传统机构的放大比有限的不足,可为兵工技术提供大尺度的精密定位。 2)该系统采用对称柔性铰链组结构,可确保系统在运动方向上无寄生位移以及系统运动方向的运动精度,从而保证系统运动过程的精密性。 3)本文系统利用二级微动放大机构附加力平衡原理,保证系统运动过程中不存在非运动方向的力或力矩,确保微驱动器不承受横向力或力矩(微驱动在非运动方向的强度一般很差),从而保证了系统运动过程中的安全性。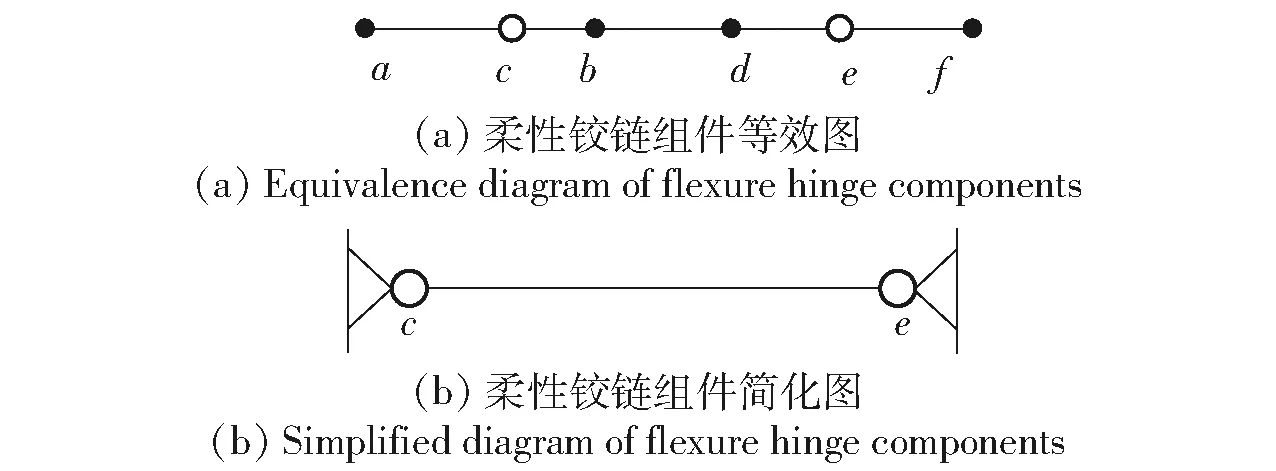
2.2 微动机构放大比计算
3 微驱动器驱动性能研究

4 二级微动放大系统性能分析
4.1 强度分析

4.2 模态分析
4.3 运动学分析

5 结论

