基于GO-Markov的飞机燃油闭环控制系统可靠性分析

李景奎，林文杰，江秀红，卢雨泽

(1.沈阳航空航天大学 民用航空学院，辽宁 沈阳 110136；2.沈阳航空航天大学 电子信息工程学院，辽宁 沈阳 110136)

0 引言

近年来，航空发动机控制系统逐渐向智能化、数字化和可视化的方向发展，其控制功能和变量不断增多。航空发动机燃油控制系统是一个闭环控制过程，其通过调节燃油流量以最佳加速率控制飞机的机动性。对飞机燃油控制系统进行可靠性分析，可以为系统设计、故障诊断和维修维护提供可靠性依据，从而提高系统的安全性。目前，系统可靠性分析方法主要有可靠性框图(RBD)[1]、二元决策图(BDD)[2]、故障模式与影响分析(FMEA)[3]、故障树(FTA)[4-5]、GO法[6-7]和贝叶斯网络(BN)[8]等。在众多系统可靠性评估方法中，GO法以其模型简洁、计算精确、有时序性、能解决多态问题等优点广泛应用于多个领域[9-13]。

GO法适用于可修和不可修系统的可靠性分析。在运用于可修系统的可靠性分析时，可修部件由操作符模拟。文献[14-15]提出并发展GO法在可修系统中的稳态定量算法。文献[16]提出一种多输入多功能可修部件的新型操作符。文献[17]提出一种多故障模式的可修系统中可靠性分析方法。文献[18]提出一种基于Bayes-GO的制动风源子系统可靠性评估方法。

在实际工程中，系统普遍存在闭环反馈控制过程，在进行系统可靠性分析过程中通常忽略闭环反馈结构，以便获得系统可靠性的近似解。闭环回路的反馈信号会给系统可靠性分析带来逻辑循环的问题，许多研究人员尝试研究闭环反馈回路对系统可靠性的影响。文献[19]提出一种在概率安全评价(PSA)中自动打破闭环反馈的分析方法，自顶向下展开了故障树的逻辑，删除故障树中导致循环的事件，从而得到无逻辑循环的故障树。文献[20]提出一种在系统层面打破系统级的闭环反馈分析方法。文献[21]提出一种求解包含闭环反馈系统故障树的有限迭代方法。文献[22-23]提出GO-Flow分析方法，采用联立布尔代数方程来描述带有闭环反馈的系统，有效解决了带有闭环反馈回路的沸水堆芯隔离冷却系统和高压堆芯注入系统可靠性问题。

一般GO法规定模型中的信号流从输入到输出形成信号流序列，模型中不允许出现闭环反馈结构[24]，避免由于系统中出现循环逻辑而无法进行计算求解的问题。文献[25]采用循环贝叶斯网络结合类型9操作符(功能操作符)来模拟具有反馈信号的部件，对带有单个闭环反馈信号的系统进行可靠性分析。文献[26]引入布尔代数思想，把构造的闭环反馈环布尔运算等式转化成GO模型，并应用于某型民用飞机襟翼液压系统的可靠性分析。文献[27-30]提出可模拟单输入、双输入和多输入闭环回路结构的新型操作符，并推导出操作符在可修系统中的可靠性计算公式。

本文根据飞机燃油控制系统原理图，建立飞机燃油控制系统GO模型。针对可修系统中含有闭环反馈环节的结构，基于马尔可夫过程理论推导出闭环回路环节在稳定状态(稳态)下的概率表达式，对某型飞机燃油闭环控制系统进行可靠性分析。将考虑反馈回路的计算方法(本文提出方法)与不考虑反馈回路的计算方法(一般GO法)和FTA法定量计算结果进行对比分析。

1 飞机燃油控制系统结构原理

1.1 飞机燃油控制系统组成

飞机燃油控制系统主要由燃油箱、滑油冷却器、高压泵、高压燃油滤、低压燃油滤、旁通活门、燃油歧管、发动机关闭阀、燃料控制单元、发动机电子控制器、燃油流量计、燃油喷雾机构等部件组成。某型飞机燃油控制系统结构原理图如图1所示[31]。

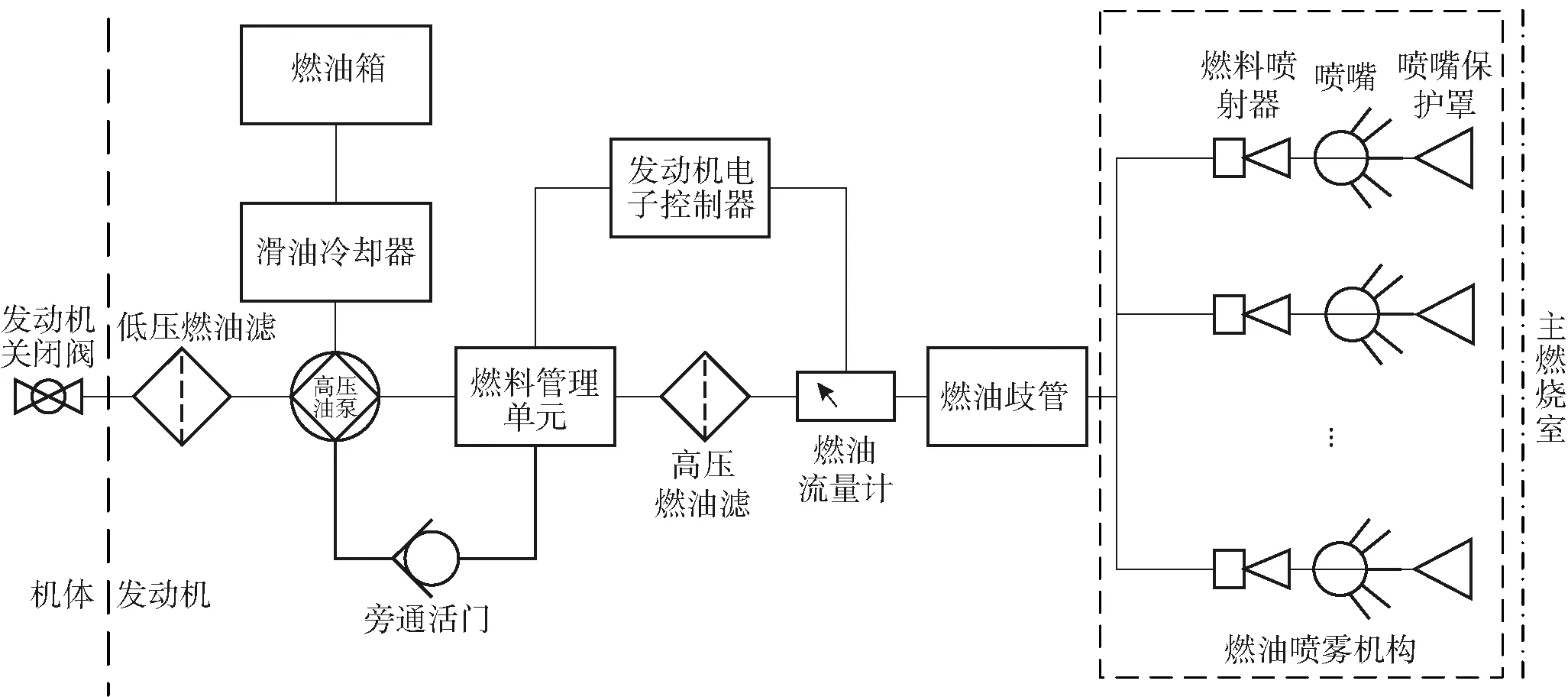
图1 某型飞机燃油控制系统结构原理图Fig.1 Schematic diagram of an aircraft fuel control system

1.2 飞机燃油控制系统工作原理

在飞机燃油控制系统中，飞机燃油经过滑油冷却器冷却后由高压油泵泵出，经过燃料管理单元、高压油滤、燃油流量计和燃油歧管，将燃油分成多条支路喷射入发动机的主燃烧室。安装在燃油管道中的燃油流量计将测量出的实时流量反馈给发动机电子控制器。旁通活门在系统释压或插转弯销后把转弯作动筒两边腔体连通，起过压保护的作用，旁通活门会发生阻塞将导致发动机空中熄火、停车等。

2 GO法分析飞机燃油控制系统

2.1 飞机燃油控制系统的GO模型构建

2.1.1 操作符的选择

GO法一共有17种基本操作符，功能操作符与实体部件逐一对应。油箱是飞机燃油控制系统燃油信号的输入，可用第5类操作符模拟；发动机关闭阀是燃油控制系统的外部信号的输入，用第5类操作符模拟；滑油冷却器、低压燃油滤、高压油泵、旁通活门、发动机电子控制器、燃料管理单元、高压油滤、燃油流量计、燃油歧管、燃料喷射器、喷雾嘴保护罩等选择第1类操作符模拟。飞机燃油控制系统GO模型的操作符类型及各部件数据如表1所示。

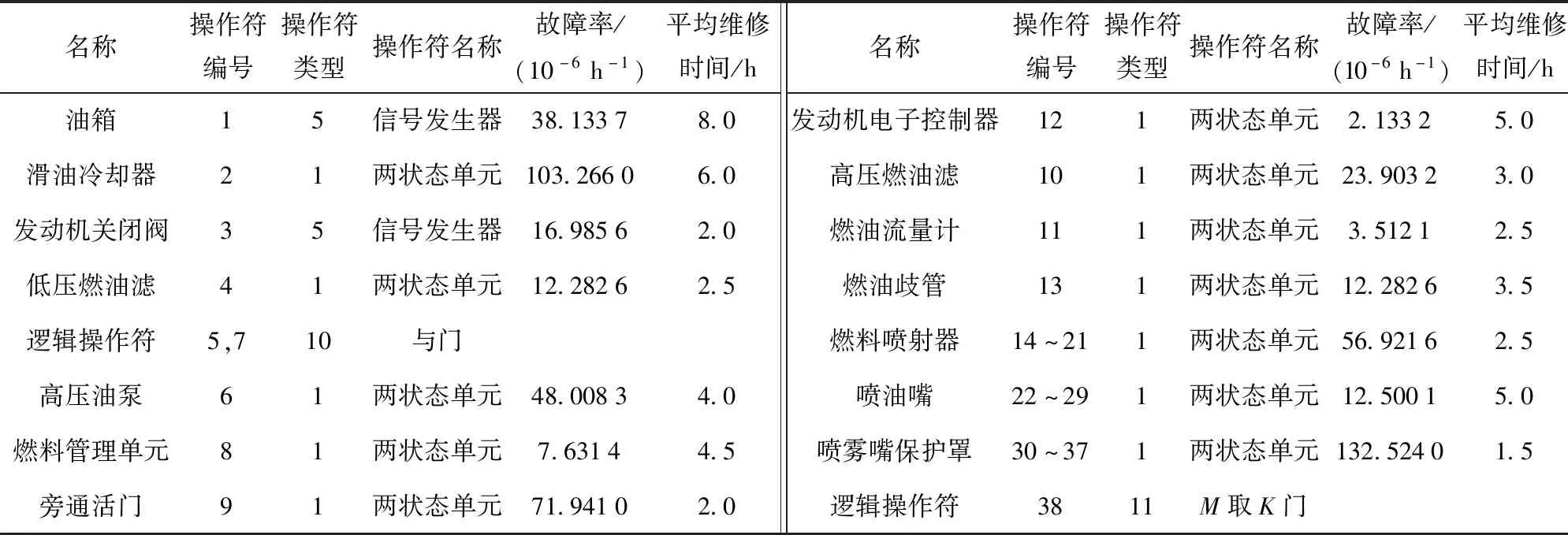
表1 飞机燃油控制系统操作符数据Tab.1 Operator data of aircraft fuel control system

2.1.2 成功准则

根据对飞机燃油控制系统工作原理的分析，以燃油控制系统对发动机正常供油为成功准则。

2.1.3 模型建立

在GO模型中，模型由操作符和连接操作符的信号流组成，信号流适用于模拟液流、电流、气流等矢量信号流。结合飞机燃油控制系统原理和成功准则，建立含闭环回路的飞机燃油控制系统GO模型，如图2所示。GO操作符内第1个数字表示操作符类型，第2个数字表示操作符编号，信号流上数字表示信号流编号，信号流38为飞机燃油控制系统正常工作的最终输出信号。

图2 含闭环的飞机燃油控制系统GO模型Fig.2 GO model of aircraft fuel control system with closed-loop

2.2 基于马尔可夫过程的闭环回路稳态可靠度分析

2.2.1 马尔可夫状态转移过程用于可修系统

马尔可夫过程中，在ti时刻的随机变量概率与tj(i,j=1,2,…,n)时刻随机变量的取值有关，与tj以前过程无关，即无后效性[32]。已知单元或系统的初始状态，可确定系统之后任意t时刻的可使用概率。采用马尔可夫过程理论分析系统可靠性时，假设系统中各个单元和等效模块的寿命与维修时间均服从指数分布，即故障率λ和维修率μ是常数[33]。在时间区间(t，t+Δt)内，未发生故障的单元发生故障的概率是λΔt，尚未修复的单元被修复的概率是μΔt；并且在较短时间Δt内出现多次故障或者修复的概率为0。

在两状态(成功状态和故障状态)可修系统中，单元或者系统始终处于正常工作与故障的交替状态，且任意状态向其他状态转移的概率之和为1。假设系统只有一个单元构成，用数字1和0分别表示部件正常工作和故障。初始条件为t=0时，P1(0)=1和P0(0)=0，即0时刻单元处于正常状态。用Pab(Δt)表示任意Δt时间内单元由a状态转移到b状态的概率(a，b=0，1)。系统的状态转移概率为

(1)

以上状态转移过程可用图3所示的系统状态转移图表示。

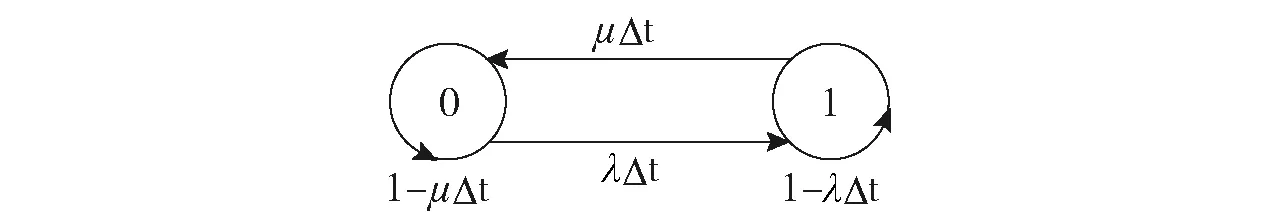
图3 系统状态转移图Fig.3 State transition diagram of the system

系统状态转移过程可写成以下状态转移矩阵：

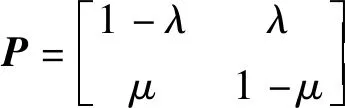
(2)

设P1和P0分别为t时刻单元正常状态和故障状态概率，取状态向量X=[P1，P0]。一段时间系统进入稳态后即t→∞时，有

XP=X

(3)

(3)式可化为X(P-I)=0，I为与P同阶的单位矩阵，可得

(4)

补充方程P1+P0=1，即可求得系统稳态下的可靠性表达式

(5)

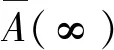
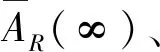
(6)

2.2.2 闭环回路稳态可靠度概率公式推导

在系统可靠性分析过程中，GO法不能计算含有闭环回路的系统可靠度，然而闭环回路作为飞机燃油控制系统的重要组成部分，燃油流量器能为电子控制器提供实时连续动态燃油流量，燃油流量大小直接影响飞机发动机的运行效率；旁通活门连通转弯作动筒两边的腔体，对燃油控制系统起过压保护及防止发动机空中熄火、停车等作用。如果忽略反馈信号对系统可靠性的影响，则最终不能有效反映飞机燃油闭环控制系统的工作特性。

马尔可夫状态转移过程适用于可修系统的可靠性分析。为方便使用马尔可夫过程理论进行系统可靠性分析，根据闭环回路环节的逻辑连接方式和GO运算法则，对闭环回路环节GO模型进行适当的等效处理。输入信号记为S，输出信号记为R；闭环回路环节中单元1-6表示为A，单元1-8表示为B，串联单元1-10和1-11等效为C[24]，单元1-9和1-12分别表示为D和E，如图4(a)所示。为便于马尔可夫转移过程的实现，将输入信号S、单元A和单元D等效为F1，将单元B、单元C和单元E等效为F2[28]，并对等效模块F1、F2和输出信号流R进行状态组合，形成闭环回路环节的马尔可夫状态转移等效图，如图4(b)所示。

图4 闭环回路环节等效图Fig.4 Equivalent diagram of closed-loop link

其中，等效模块C执行串联可修系统的GO算法，其表达式为

(7)

式中：PC(1)和PC(0)分别为等效模块C在成功状态和故障状态下的概率；PC10(1)和PC11(1)分别为操作符10和11在成功状态下的概率；PC10(0)和PC11(0)分别为操作符10和11在故障状态下的概率；λ10和λ11分别为操作符10和11的故障率；λC和μC分别为等效模块C的故障率和维修率。

等效模块F1的运算规则是部件S与D作逻辑与门运算之后，再与A作GO运算；等效模块F2的运算规则是部件C与E作GO运算之后，再与B作逻辑与门运算，则有

(8)

式中：λS、λA、λB、λD、λE、λF1、λF2分别为S、A、B、D、E、F1、F2的失效率；μS、μA、μB、μD、μE、μF1、μF2分别为单元S、A、B、D、E、F1和F2的维修率。

根据等效模块F1、F2和输出信号R的工作状态，列出闭环回路环节状态组合表，如表2所示。表2中数字0和1分别表示故障状态和成功状态，状态组合0表示系统的成功状态，状态组合1、2、3均表示系统的故障状态。

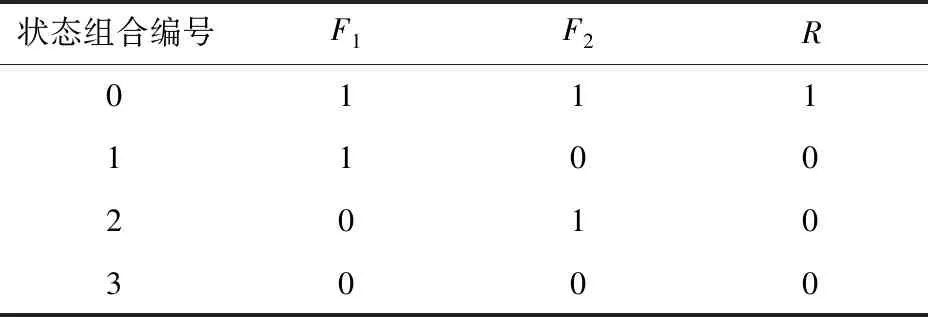
表2 闭环回路环节状态组合表Tab.2 State combination table of closed-loop link

由等效闭环回路环节的4个运行状态组合，绘出闭环回路环节的马尔可夫状态转移图如图5所示。

图5 闭环回路环节的马尔可夫状态转移图Fig.5 Markov state transition diagram of closed-loop link

设闭环回路环节的状态转移向量S=[P0，P1，P2，P3]，P0、P1、P2、P3分别表示等效闭环回路环节在t时刻处于0、1、2、3状态组合的状态概率。由图5写出闭环回路环节的马尔可夫状态转移概率矩阵G为

(9)

可修系统在开始工作时，系统可用度A(t=0)=1，可用度随着设备工作时间增加而逐渐减小，工作一定时间后系统进入稳定工作状态即t→∞时，有

SG=S

(10)

(10)式转化为S(G-I)=0。由归一化条件，即任意时刻取每个状态概率之和等于1，得

(11)

由(9)式～(11)式，得

(12)

闭环回路环节输出信号R在稳态下的等效故障率λR和等效维修率μR通过(13)式求解：

(13)

则闭环回路环节的输出信号R在稳态下有

(14)

式中：PR(1)和PR(0)分别为闭环回路环节输出信号R在稳态下成功概率和故障概率。

2.3 可靠性计算

根据本文给出的闭环回路环节计算方法和一般GO法的运算规则，列出含有闭环回路GO模型中关键信号流的表达式。

2)信号流11：即闭环回路输出信号R，PR11(1)=PR(1),PR11(0)=PR(0),λR11=λR，μR11=μR。

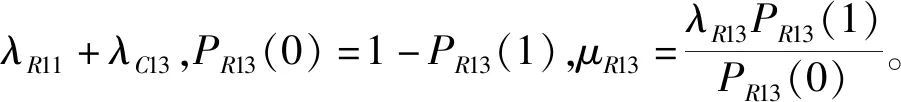
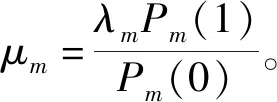
在飞机燃油控制系统中，假设燃油喷雾机构中8条支路至少有6条正常工作，能为飞机发动机提供持续稳定的供油，即M=8，K=6。系统最终输出信号流38在稳态下的成功状态概率计算公式为

通过代入数据计算，输出信号流38在稳态下的成功输出概率为0.998 477 35。

3 对比分析

3.1 一般GO法对燃油控制系统可靠性分析

在一般GO法中，为避免闭环回路环节反馈信号带来循环逻辑计算困难问题，通常会忽略系统中闭环回路环节的反馈信号，以便获得系统近似可靠度。本节采用第5类GO操作符(信号发生器)模拟两个反馈信号，计算过程中将两个反馈信号的失效率设置为0，建立不含闭环回路的飞机燃油控制系统GO模型，如图6所示。

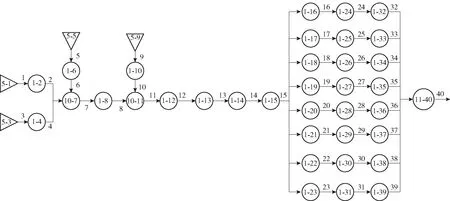
图6 不含闭环回路的飞机燃油控制系统GO模型Fig.6 GO model of aircraft fuel control system without closed-loop

根据一般GO法运算规则，列出不含闭环回路的飞机燃油控制系统GO模型中主要信号流的表达式如下：

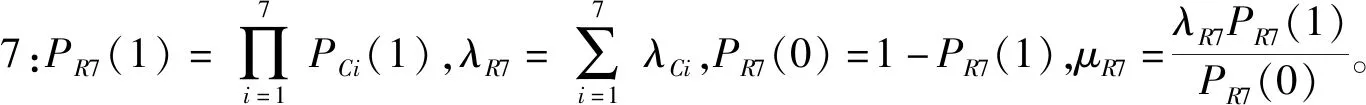
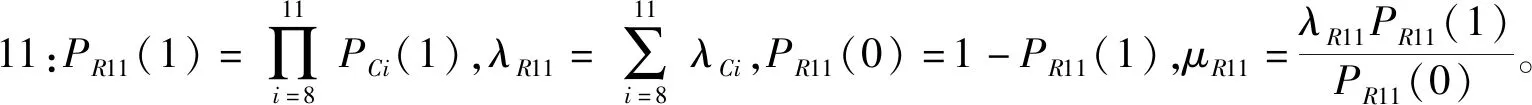
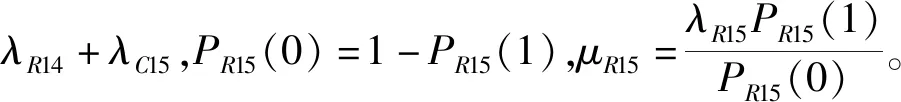
5)信号流40：

通过代入数据计算，一般GO法计算出信号流40在稳态下的成功输出概率为0.998 507 62。

3.2 FTA法对燃油控制系统可靠性分析

FTA法是一种系统可靠性与安全性评估方法，广泛应用于系统可靠性和安全性分析。以飞机燃油控制系统故障为故障树的顶上事件，建立飞机燃油控制系统FTA模型，如图7所示。

图7 飞机燃油控制系统FTA模型Fig.7 FTA model of aircraft fuel control system

由图7可见，飞机燃油控制系统FTA模型中，共有12个中间事件和14个底事件，其中T表示燃油控制系统故障，M1表示供油失效，M2表示燃油流量控制失效，M3表示燃油喷雾机构失效，M4表示燃油传输故障，M5～M12表示8条燃油喷雾机构中任意一条支路故障；M13表示油滤故障。飞机燃油控制系统FTA模型中对应的底事件如表3所示。

表3 飞机燃油控制系统故障树底事件Tab.3 Bottom events of aircraft fuel control system fault tree

通过代入数据计算，用FTA法计算出飞机燃油控制系统在稳态下成功概率为0.998 507 64。

3.3 对比分析

本文方法与一般GO法和FTA法对飞机燃油控制系统的可靠性计算结果对照如表4所示。

表4 不同方法定量计算结果Tab.4 The results of quantitative calculation by different methods

从表4中可以看出，本文方法计算结果略低于一般GO法及FTA计算结果。针对同一系统，一般GO法在处理闭环反馈环节时以第5类操作符进行运算，并设置两反馈信号失效率为0，计算结果略高于系统真实可靠度。在使用FTA的计算过程中未考虑反馈信号的失效，也不能进行状态转移的计算，因此计算结果并不完全准确。本文方法通过马尔可夫模拟状态转移，考虑了反馈系统的所有失效可能，结果更能反映系统可靠性的真实情况。

4 结论

本文将闭环回路环节进行等效替代处理，采用马尔可夫状态转移过程理论对闭环回路进行状态组合，推导出闭环回路环节的状态概率计算公式，解决了一般GO法不能计算含有闭环回路系统的可靠性问题。得出主要结论如下：

1) 闭环回路环节的反馈信号对系统的可靠性有影响。

2) 通过采用本文方法与一般GO法和FTA法对某型飞机燃油控制系统的可靠性计算对比，本文方法考虑反馈信号对系统可靠性的影响，该计算方法能更真实地反映系统的可靠性。