审意·培思·论证：初中几何概念教学策略探究

王宁

概念是数学课程中较为常见教学内容。学术界将“概念”定义为“反映对象本质属性的思维形式”，可见，数学概念教学既要体现对数学对象本质属性的研究，其中更蕴含对学生数学思维形式发展的教学要求。几何是初中数学重要组成，几何概念学习是学生探究初中几何基础与保障。所谓“代数繁”“几何难”，加强几何概念教学策略研究，对促进初中数学教学有重要现实意义。本文以苏科版初中数学教材为例，就此话题展开讨论。

一、初中数学几何概念形式

初中几何研究对象繁多，涵盖点、线段、直线、直线关系、夹角、图形（三边形、四边形、多边形、圆形）等，通过概念学习来厘清几何图形性质，增进对几何图形认知。发展几何思维能力，是初中阶段几何概念教学关键点。纵观初中数学几何概念表现形式大致可分为如下几种形态：

1.文字描述型

某些几何图形与人们日常生活关系紧密。学生借助已有生活阅历，对其已经具备了相应认知能力，只是苦于或无力对其进行准确描述，这种情况下，教材通常会以“白描”方式将其概念直接以文字形式予以显示。如，七年级上册“平面图形的认知（一）”中关于“点到直线的距离”概念，直接表述为“直线外一点到这条直线的垂线段的长度叫做点到直线的距离”;再如七年级下册“平面图形的认识（二）”中对三角形的定义，则直接用文字表述为“三角形是由3条不再同一条直线上的线段，首尾一次相接组成的图形”;還有九年级上册《对称图形——圆》中“正多边形”概念为“各边相等、各角也相等的多边形叫做正多边形”等。

2.图形辅助型

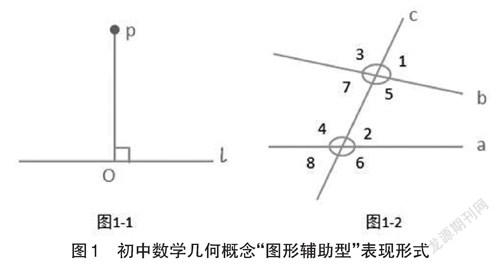
有些几何概念从图形中抽象而来，或需从图形关系中产生，因而在概念表述时需借助图形降低学习理解难度，或反映概念中各种因素几何关系。通过图形诠释概念，体现对学生几何直观、空间观念与模型思想等数学思维的教学渗透。如，七年级上册“平面图形的认知（一）”中对“垂线段”的几何概念定义，则利用了图形辅助（见图1-1），教材描述为“如图，点P在直线l外，PO⊥l，垂足为O，PO叫做点P到直线l的垂线段”。再如，七年级下册“平面图形的认识（二）”中对“同位角”“内错角”“同旁内角”等几何概念表述时，也均借用了图形辅助（见图1-2），体现上述概念中不同几何图形关系。

3.符号标识型

将几何图形进行抽象化，将图形所涵盖的本质属性以数学符号形式予以展示，体现几何概念中的应用原理，在初中数学教材中也较为普遍。符号化的几何概念，既是对归纳、符号意识、模型思想等数学思维教学引导，也是对数学学科规范严谨特点的认知渗透。如，七年级上册“平面图形的认知（一）”中关于“平行线”几何概念，既体现了“在同一平面内，不相交的两条直线叫做平行线”文字定义，用通过“两条直线相互平行，记作a∥b或者AB∥CD”给予符号标识。再如，九年级上册《对称图形——圆》中有关“圆”“圆弧”几何概念，提到“以点O为圆心的圆，记作‘⊙O，读作‘圆O”，“圆上任意两点间的距离叫圆弧，简称弧，用符号‘⌒表示”等等。

二、初中数学几何概念教学策略

几何概念源于数学概念，具备一般数学概念基本特征。教学过程中应遵循数学课程规律与学生认知特点，以生为本，引导学生在接触几何概念时主动进行知识建构。与此同时，教师也应摒弃大包大揽、满堂灌输等传统教学方式，在思维引导和认知结构构建方面予以积极引导，促使学生在几何概念学习中取得更好成果。以笔者实践为例，关于初中数学几何概念教学可从如下几方面进行优化：

1.审意：重视几何语言研读

几何概念由几何语言构成，几何语言有其独特逻辑规范与叙述风格。前文提到的“文字语言”“图形辅助”“符号标识”等，均体现不同情境下几何语言对几何的完美诠释。笔者发现：几何方面表现不佳学生，多半根源出在对几何概念理解偏差方面，由于认知不深、解读不全，严重影响他们在几何应用与题型证明等方面表现。因此，加强对几何概念中几何语言教学研读，培养学生透过几何概念深入探寻其中数形关系，则有助于提升学生几何学习表现。

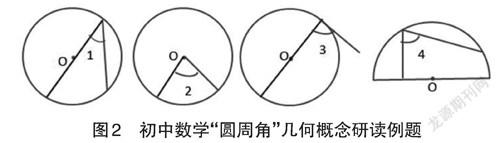
以九年级上册《对称图形——圆》中“圆周角”概念教学为例。关于“圆周角”，教材给出的定义是“顶点在圆上，并且两边都和圆相交的角”。这个概念的形成，至少包含两个条件：（1）角的顶点要在圆上;（2）角的两边要全部和圆相交。那么，这个概念在解读过程中就会有“疑问点”，有学生就问到：什么是“和圆相交”？结合图形，在深入理解探究过程中，学生们发现：“和圆相交”即是圆周角的两边都必须有“两点”在圆上面。可通过以下例题进行佐证（见图2）：以下图形中各角，哪几个是⊙O的圆周角？（  ）A，∠1 ;B、∠1、∠4;C、∠1、∠3、∠4;D、∠1、∠2、∠3、∠4。本题关键在于对“圆周角”概念理解，通过概念中必要条件（1）“角的顶点在圆上”，则可以排除∠2，实际上∠2是⊙O的圆心角。虽然∠1、∠3、∠4符合概念中的条件（1），那么它们是否符合第（2）个条件“两边全部和圆相交”呢？∠1两边有两点在圆上，因此很容易判定其符合题意。∠3只有一条边与⊙O相交（有两个交点），另一边只有一个交点，所以∠3不合题意;∠4情况略显特殊，虽然是角与半圆关系，但通过补圆，我们发现其同样符合“圆周角”概念条件中“顶点在圆上”“两边都与圆相交（两边都与圆有两个交点）”条件，符合题意。因此，本题答案为B。

2.培思：加强几何图形探究

几何是与图形相关数学，几何概念学习的前提建立在学生对几何图形深入研究基础之上，建立在学生对图形性质快速识别、准确依据几何语言快速画出几何图形及围绕几何图形快速展开计算应用等基础之上。初中数学几何概念的导入、公式定理的阐述证明等等，均离不开学生对几何图形的深入理解，体现几何概念与识图读图能力互相促进的教学关系。引导学生加强对几何图形的深入探究，实则体现对通过几何思维培育，为几何概念理解与应用奠定坚实基础。32CC6605-ECCA-467E-BFFD-7F8E024C8405

以八年级上册“轴对称图形”某习题为例。如图（见图3）已知A、B、C三点均处于方格纸格点之上，请再找一个格点D，使A、B、C、D四点组成一个轴对称图形。本题需画图解决，前提建立在学生对几何图形深入理解基础之上。通过本题探究，可深化学生对“轴对称图形”这一几何概念认知。解题前，首先要借助前文“几何语言”研读策略，深入探寻题干与问题核心。题目共中有哪些条件？题目要求取得什么结论？通过读题，不难得出本题给出两个条件：（1）三点固定（A、B、C）;（2）新的四边形ABCD是轴对称图形。而找到D点的关键，最终落在解决“如何确定对称轴”问题之上。可通过（1）以线段AB的垂直平分线为对称轴，找到C点的对称点D（见图3-1）;（2）以线段BC的垂直平分线为对称轴，找到A点的对称点D（见图3-2）。但是，很多学生往往忽略了将图中已知线段AB、BC、AC本身作为对称轴的作图方法，因而缺少了其他解法（见图3-3、图3-4，注：因以AC作对称轴时B点对称点D不在格点上，故舍弃）。

3.论证：强化概念过程推演

几何概念是对几何现象规律进行判断、推理与建构的重要依据，也是培养学生数学思维，启发数学能力的重要开始。初中数学教材中编排的几何概念，既是阶段性教学目标任务的综合体现，更建立在学生既有数学能力基础之上。因此，在教学过程中，教师应重视引导学生对几何概念形成过程深入探究，鼓励学生通过推导、验算、论证等方式对几何概念成因序列展开推演，以深刻揭示概念之间的相互关联及内在本质属性特征。

以“等腰梯形”概念探究教学为例。对于等腰梯形，常见的判定概念是“同一底上的两个角相等的梯形是等腰梯形”，那么，这个概念该如何证明？有人认为“对角线相等的梯形是等腰梯形”，你觉得这个概念是否正确？该如何证明？将几何概念中的文字描述，转化为实际推导验算过程，是培养学生深入理解几何概念重要途径。课堂教学中，笔者将上述两种与等腰梯形相关概念转化为数学问题论证，引导学生通过概念形成过程的推导，强化对等腰梯形性质特点认知。对第一种说法，可转化为如下数学论证问题：在梯形ABCD中（见图4），已知AD∥BC，∠B=∠C，求证：梯形ABCD是等腰梯形。学生通过研读题意，很快找到的解题方法。沿梯形两个腰BA与CD做延长线，交于F点（见图4-1），构成一个全新三角形△BFC。因为∠B=∠C，所以△BFC为等腰三角形，所以FB=FC;又因为AD∥BC，所以∠FAD=∠FDA，所以△FAD為等腰三角形，所以FA=FD;因为AB=FB-FA，DC=FC-FD，FB=FC，FA=FD。所以，AB=DC;所以，梯形ABCD为等腰梯形。关于“对角线相等的梯形为等腰梯形”概念论证可通过如下具体问题予以实现：在梯形ABCD中，已知AD∥BC，AC=BD，求证：梯形ABCD是等腰梯形。学生的论证过程为：过D点作DF∥AC交BC于F（见图4-2）。因为AD∥BC，DF∥AC，所以四边形ACFD为平行四边形，所以DF=AC=BD，所以，∠DBC=∠DFC。因为DF∥AC，所以，∠ACB=∠DFC=∠DBC，根据三角形全等（SAS）判定公式，可得出△ABC≌△DCB，所以，AB=DC;所以，梯形ABCD为等腰梯形。通过这样的论证与推演，不仅解决了学生对“等腰梯形”概念形成过程的亲身体验，深化学生对几何概念隐含图形属性的根本性认知，更通过对相同几何概念不同表述的验证判断，拓展数学思维，发展推理归纳能力。

综上所述，几何是初中数学的重要组成，是“数学是研究空间形式的科学”定位的核心要素。几何概念隐含对数学符号意识、空间观念、几何直观、推理能力以及模型思想的启蒙与熏陶，是初中几何教学的先导，更是几何应用的前提。本文从几何概念的常见表达形式入手，探究了几何概念教学研究重点。从审意、培思、求证等方面探究几何概念教学策略，引导教师从重视几何语言研读、加强几何图形探究、强化概念过程推演等途径来展开几何概念教学，让学生从中不仅获得数学知识，更可收获尺规作图经验，通过内化能力、外化建构方式，提升几何概念教学效果，为培养学生数学核心素养而不懈努力。32CC6605-ECCA-467E-BFFD-7F8E024C8405