让稚朴的表达多“飞”一会儿

涂俊珂

曹培英教授曾说：“唯有基于儿童、基于数学，才能实现学生学业与教师发展的最大化。”好奇、爱玩、乐分享是孩子的天性，在课堂教学中应遵循儿童的天性，和谐的课堂既有学生个体的独立思考探索，也要有同伴间的智慧碰撞、群体的交流分享。我们鼓励孩子用童言童语“讲数学”、诠释自己对数学概念的理解，让儿童在思辨中获得正确的认识，深化对知识的理解。

下面让我们先来看看发生在一节数学课上的对话：

“它在孤军奋战”“原来有团伙帮忙呀”“一个人打不赢啦”……这是在讲故事吗？No，no，no，此乃数学课堂上孩子们有趣的对话。

“猴子的烦恼”是北师大小学数学三年级下册第一单元“除法”第四课时的内容，本课主要学习三位数除以一位数，被除数中有0，商中间或末尾有0的除法。课堂上，在理解了“0除以任何不是0的数都得0”之后，通过306÷3，探索被除数中有0的除法计算。

借助小正方体模型，学生能很快建立口算与除法竖式之间的内在联系，理解竖式的计算方法。

在完成了306÷3的竖式计算后，课堂上有了下面这段对话。

师：这道题与前面学的除法有什么不一样吗？

生：这道题出现了0。

生：是被除数和商里都出现了0。

师：为什么商的中间会有0呢？

生：因为被除数的中间有0，0除以除数3就等于0。

师：哦，原来是这样。那我们再来算算306÷2这道题吧。

……

少顷，有的孩子们轻声嘀咕起来：这道题的商中间没有0了。

师：同学们有什么发现吗？

生：我发现306÷3，商的中间有0，306÷2，商的中间没有0。

师：都是中间有0的306做被除数，为什么一题商的中间有0，另一题商的中间没有0呢？

生：306除以3时，0一个人在打仗，打不赢呀！

生：是的是的！0在孤军奋战，0打不赢3，就只能商0了！

师：那306÷2呢？

生：306在除以2時，0有团伙帮忙了！

师：哦，还有团伙呀！你们猜猜××说的“团伙”是谁？

生：团伙是百位剩下的（余数）1；

生：这个1可以变身为10个1，0有了10帮忙，就能打赢除数3了！

师：请问被除数的中间有0，商的中间一定有0吗？

生：那可不一定，要看这个0是不是在孤军奋战。

生：如果中间的0一个人打仗，那商的中间一定有0，如果0有余数团伙帮忙，商的中间就没有0了。

……

哈哈，有意思！这帮小家伙把除法计算看作“打怪升级”游戏了！我在脑海里迅速思量：是马上出手把孩子们的表达拉回到“中规中矩”的标准语言上，还是和他们一起继续“打怪升级”呢？几乎没有犹豫，当即决定：让这可爱稚朴的表达多“飞”一会儿吧！

下一节课“节约”，学习“三位数除以一位数、被除数中没有0，因不够商1而在商中间或末尾商0的除法”，我们继续保持“打怪游戏”的对话体系。

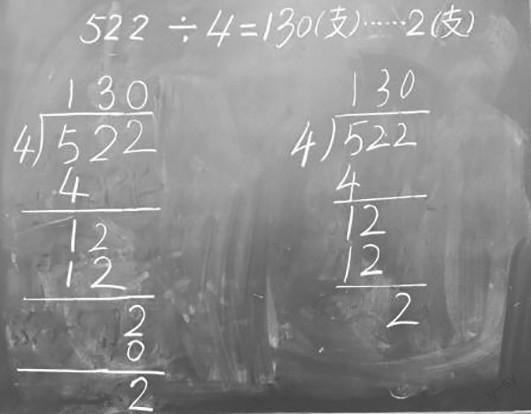
师：912÷3、522÷4 这两道题的被除数里都没有0，可是为什么商的中间或末尾有0呢？

生：912÷3，十位上的1一个人打不赢3，只能商0。

生：是的，522÷4也是这样，末尾的2没有团伙帮忙打不赢4，就要商0。

师：你们说的“打不赢”究竟是什么意思呢？

生：1比3小，2比4小，不够除当然打不赢

生：“打不赢”就是连1都商不了，所以只能商0。

生：我想补充一个前提，要分的那个数自己比除数小，而且又没有团伙帮忙就肯定打不赢。

师：哦，既然都打不赢了，0不写行吗？

生：不可以，不写0就等于没打仗呀！

生：0不写，商就变成两位数了。

师：想一想，决定商是否有0的关键是什么呢？

生：我举个例子吧，比如：522÷4，除到被除数的个位，只有当个位上的数比4小打不赢4，而且没有团伙帮忙的时候，商就一定有0；如果个位上的数比4大，或者有团伙帮忙，商就不会出现0了。

生：我想补充一下，个位上的数如果和4一样大，打成平手，就可以商1，商也不会出现0。

生：我认为决定商是否有0的关键是看接下来要分的数，自己能不能打赢除数，如果自己打不赢再看有没有团伙帮忙。

师：会不会出现有团伙帮忙都打不赢除数的情况呢？

生：不可能的！团伙可以变身的！

师：哦？怎样变身？

生：我举个例子吧，百位如果余1，“1”来帮忙就变身为10个10，十位如果余1，“1”来帮忙就变身为10个1，这样一定能打赢除数了。

生：有团伙帮忙，就可以合体变成两位数了，两位数肯定能打赢一位数。

……

爱了爱了！孩子们的表达原来可以如此精彩！可爱的童言童语生动形象地解释了“三位数除以一位数”的计算道理。我们把“孩子的话”与“老师的话”做个对照：

瞧，“孩子的话”与“老师的话”放到一起并不违和。“遇到被除数的那一位上的数，除以除数不够商1（前一位没有余数）就商0”这是作为成人的教师的“明白”，“团伙帮忙打得赢，打不赢的时候就商0”这是作为儿童的学生的“明白”。如何让孩子们用自己的“明白”理解我们的“明白”？

我想首先应努力做到的是不急于让孩子明白我们的“明白”。孩子的世界充满想象，如果“天马行空地打仗”有助于他们对除法算理的理解，那让这可爱的表达多“飞”一会儿又有何妨！只是做一个“能忍”的教师并非易事，有时一不留神，老师就成了“真理评判者”，久而久之，孩子们会习惯去猜“你想让他说什么”，不再专注于“我想说什么”，从而失去本真的表達。不妨蹲下来以儿童的视角真正参与他们的对话，你会发现让稚朴的表达多“飞”一会儿是一件很美妙的事情！

其次，该出手时就出手。老师适时抛出一个个问题，“你们猜猜他说的‘团伙是谁？”“你们说的‘打不赢究竟是什么意思呢？”“既然都打不赢了，0不写行吗？”“会不会出现有团伙帮忙都打不赢除数的情况呢？”“决定商是否有0的关键是什么呢？”一个个问题的抛出，搅动思维的涟漪，引发一个个思维高潮。这些问题有的在引导孩子去读懂同伴的表达，有的“逼”着孩子去解释原因、讲道理，有的帮助学生捅破最后一层“窗户纸”深刻理解算理、有的助力学生完成思维的升级……孩子们在思辨中不知不觉用自己的“明白”理解了我们的“明白”！

数学是严谨、抽象的，而儿童以直观形象思维为主，只有处理好了两者之间的矛盾，才能让孩子学好数学。这场相互讨论、倾听、补充、调整、沟通与分享的学习过程，让我们看到儿童熟悉的话语好玩、有趣、易懂，更容易让儿童产生亲近感。鼓励孩子敢讲话、会表达、善提问，大胆用自己的童言童语表达内心的数学世界，方能引发真正的思维共振，感受数学学习的乐趣与价值。