单次扫描连通域分析算法研究综述
曲立国,陈国豪,胡 俊,陈 鹏
(1. 安徽师范大学物理与电子信息学院,安徽芜湖 241002;2. 安徽省智能机器人信息融合与控制实验室,安徽芜湖 241002)
1 引言
连通域标记(Connected Component Labeling,CCL)和基于CCL 改进的连通域分析(Connected Component Analysis,CCA)是二值图像分析和图像处理的重要步骤,在医学[1~3]、自动监控系统[4~6]、天气监测[7]、人脸识别[8]和天文观测[9]等诸多领域有广泛应用. 它对二值图像中前景像素(也称对象像素)进行标记,让每个单独的连通域形成一个被标识的块,进而获取这些区域的面积、边界框和质心等相关图像特征信息.
为了不失一般性,在W×H像素大小的二值图像中,坐标为(x,y)的像素表示为b(x,y),其中0≤x≤W-1,0≤y≤H-1. 图像内像素值只有0 和1,假设0 代表背景像素,1代表前景像素.
CCL 算法常见的连通关系有四连通和八连通两种,如图1 所示. 任意像素b(x,y)的上下左右四个像素,即b(x,y-1),b(x,y+1),b(x-1,y),b(x+1,y)被称为它的四连通像素. 四连通像素加上四个对角相邻像素,即b(x-1,y-1),b(x+1,y-1),b(x-1,y+1),b(x+1,y+1)被称为它的八连通像素.

图1 四连通和八连通
根据图1的连通关系,相互连通的对象像素属于同一个连通域. 连通域标记就是给属于一个连通域的所有对象像素分配相同标签,利用唯一的标签区分图像中不同连通域. 连通域是一副图像中相互连通的对象像素的最大集合,所以一个连通域也可以被称为一个物体对象.
自20 世纪60 年代以来,大量学者致力于连通域标记算法的研究. Rosenfeld 等人[10]和Lumia 等人[11]设计了基于像素的连通域标记算法;Ronse等人[12]设计了基于游程的连通域标记算法. 现代算法都是在它们的基础上发展而来的,根据算法通过图像的扫描次数的不同,其可以分为以下几类:(1)多次扫描标记算法[13,14];(2)基于轮廓跟踪的标记算法[15~18];(3)两次扫描标记算法[19~39];(4)单次扫描标记算法[40~68].
已有一些文章对CCL 算法进行了比较. 文献[30]对文献[10,11,15,25~28]中提出的算法进行了综述,并提出了用于测试不同算法性能的基准. 此外,文献[35]对基于标签传播[15]和基于标签等价解析[22~26,32]的标记算法进行了综述,详细介绍了一些典型算法的原理,并给出了一些算法的伪代码. 但这些比较综述主要针对两次扫描CCL算法,很少提及单次扫描算法.
单次扫描连通域标记算法又称为单次扫描连通域分析(CCA),也有文献对CCA 算法进行了比较. 文献[50]对一些现有CCL 和CCA 算法进行了比较,然而这篇文章对除了文献[48]算法以外的所有算法都只是进行了简单的描述,并没有详细说明算法的原理和算法之间的联系. 为此本文对最近十年来发展的单次扫描CCA 算法进行分析,描述适用于单次扫描CCA 算法的联合查找算法,阐述典型CCA 算法的原理,给出它们的伪代码,并对算法FPGA 性能的实现情况进行了比较.
2 联合查找算法
无论是在CCL 算法还是CCA 算法中,标签等价关系的记录和处理都是算法实现的重要操作,并且影响着算法处理效率. 联合查找(Union-find)算法是记录和解析标签等价关系的一种有效方法[50],它通过一个联合查找森林结构实现,森林由相互独立的联合查找树组成. 联合查找树的特点:(1)给每个连通域分配的临时标签都是树中的一个结点,每个结点都连接到它所在树中的父结点;(2)树中的所有结点都是等价的,一棵树代表一个连通域;(3)如果树中一个结点的父结点就是它本身,那么该结点被称为该树的根结点,根结点是树中最小的标签,对应着该树代表连通域的根标签.
可以采用图像进一步表示联合查找树算法的结构,做以下定义:结点Ni通过有向边指向另一个结点Nj,有向边E可以表示为Ni→Nj,其中Ni是Nj的子结点,Nj是Ni的父结点. 一个结点可以有很多子结点,没有子结点的结点是叶结点. 所有结点的集合N(F)和有向边集合E(F)构成森林F,如式(1)所示:
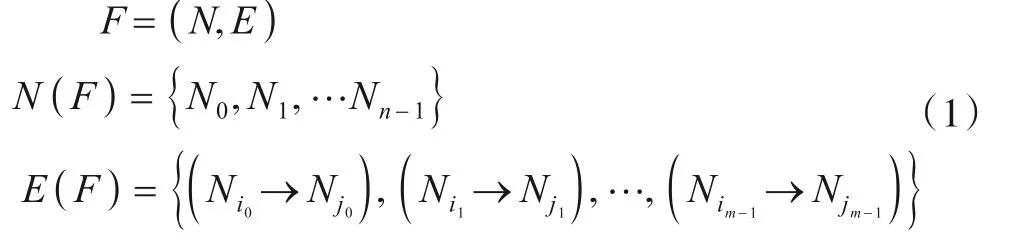
每一个结点都沿着一条路径连接到树的根结点,路径中有向边E的条数就是该结点的等级. 根结点的等级为0,其它结点比它的父结点等级高1,叶结点的等级最高,树中叶结点的等级就是这棵树的高度. 两个连通域和它们对应的联合查找树结构F如图2所示.

图2 连通域示例和联合查找树数据结构F
联合查找树已经衍生出多种改进算法,如快速查找(QuickFind)算法[37]、快速联合(QuickUnion)算法[37]和带有路径压缩的快速联合(QuickUnion with Path Compassion)算法[37]. 在单次扫描CCA 算法中,一种有效的联合查找算法是文献[50]中提出的基于上下文(Context-based)的联合查找算法,它不仅结合了快速查找和快速联合的最佳特性,还加入年龄平衡(Agebalancing)[39]策略. 年龄平衡策略不再依据标签数值大小定义标签大小,而是依据分配标签的时间先后顺序(即标签“年龄”),越早分配的标签年龄越大,标签越小. 年龄平衡策略可以确保给连通域分配的初始标签始终是根标签,避免许多复杂的合并,简化了算法计算复杂度.
基于上下文的联合查找算法伪代码如算法1所示,它主要包含新树(Newtree)、查找(Find)、联合(Union)和展平(Flatten)四个操作. 当给新连通域分配新标签时,将会在森林中创建一个新树,树的根结点n指向自己. 通常,查找操作会迭代找出结点的根结点[38],但算法1中查找操作只找出结点n的父结点. 在联合操作中连接结点u和v,需要对两个结点进行一次查找,找出它们的父结点e和f. 当e小于f时,把e作为f的父结点;而当e大于f时,不仅要把f作为e的父结点,还需要把这两个合并标签压入链堆栈中保存. 展平操作在图像每一行行尾执行,将链堆栈中的标签反向弹出,把较小标签的父结点作为较大标签的父结点,从而解析两个标签的等价关系.
3 连通域标记
表1 从以下几个方面对典型CCL 算法和CCA 算法的性能进行了比较:(1)扫描次数和连通性;(2)扫描和标记单元;(3)运行时间复杂度和采用的等价解析策略;(4)是否重用标签. 图3 列举了CCL 算法和CCA 算法主要的扫描窗口,其中图3(d)是文献[54]中提出的TRSP(Tang’s Run-based Single Pass)算法的扫描窗口,该算法将会在4.2.1节分析.
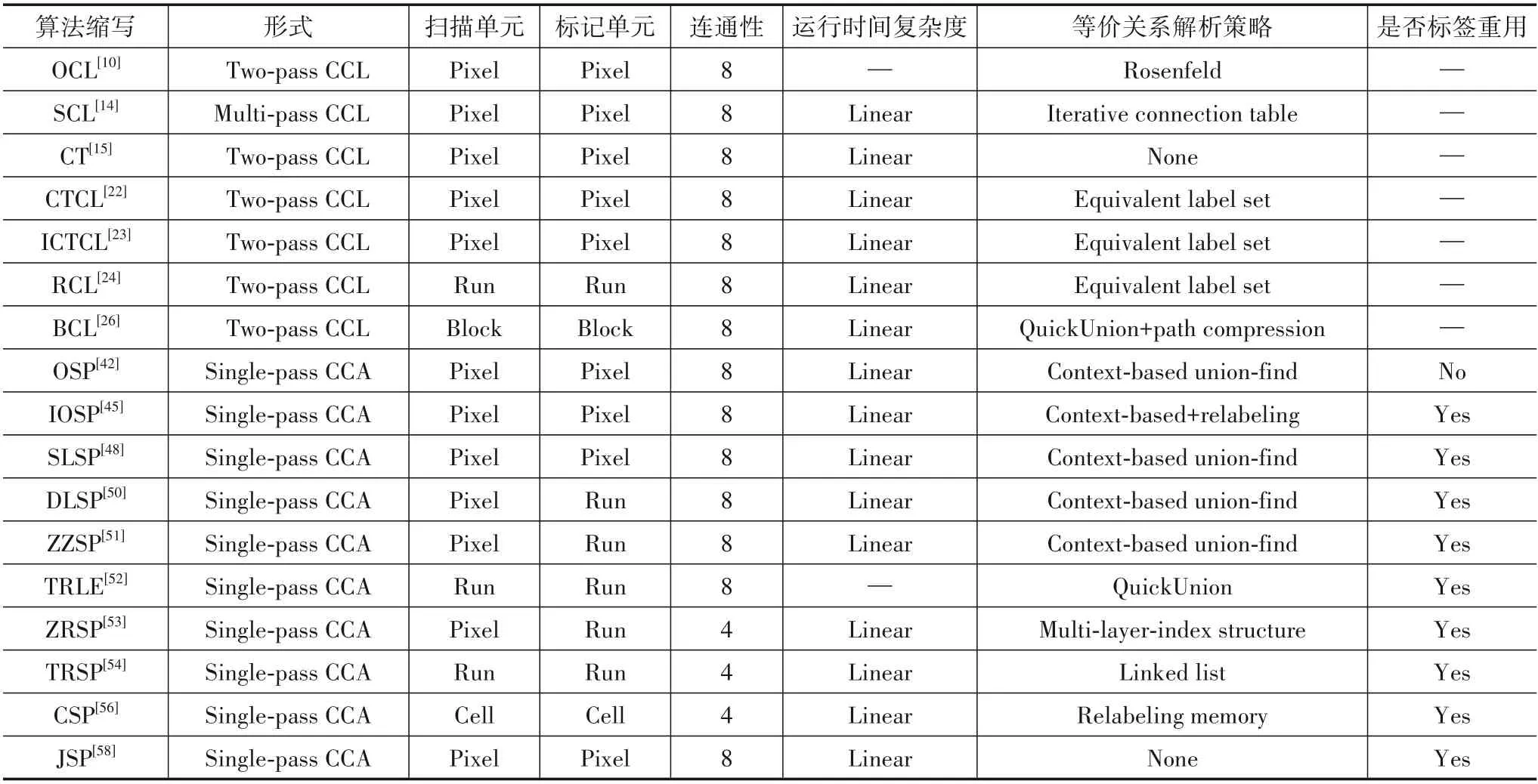
表1 典型CCL和CCA算法的性能比较
Rosenfeld 等人[10]在1966 年提出的OCL(Original Connected-component Labeling)算法是经典连通域标记算法,它采用如图3(a)所示的扫描窗口对输入图像进行两次扫描并生成一个包含标记结果的输出图像. 第一次扫描图像时给像素分配临时标签:当前像素如果是背景像素,则标记为0;如果是对象像素,需要根据四个邻域像素信息为当前像素选择临时标签. 如果邻域都是背景像素,则分配一个新标签;如果邻域内只存在一个标签,则把该标签分配给当前像素;如果邻域中存在两个不同标签,则把较小标签分配给当前像素,并在等价表中记录两个标签的等价关系. 第二次扫描图像时用等价表中的代表标签(连通域中最小的标签)替换所有临时标签.OCL 算法需要为最终图像和等价表分配足够的内存,并且由于在检测等价关系时重复采用排序算法,计算量较大.

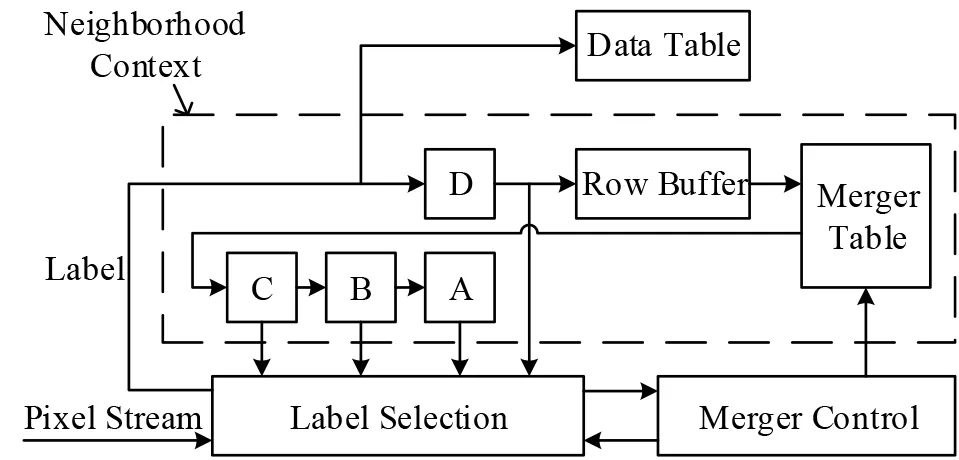
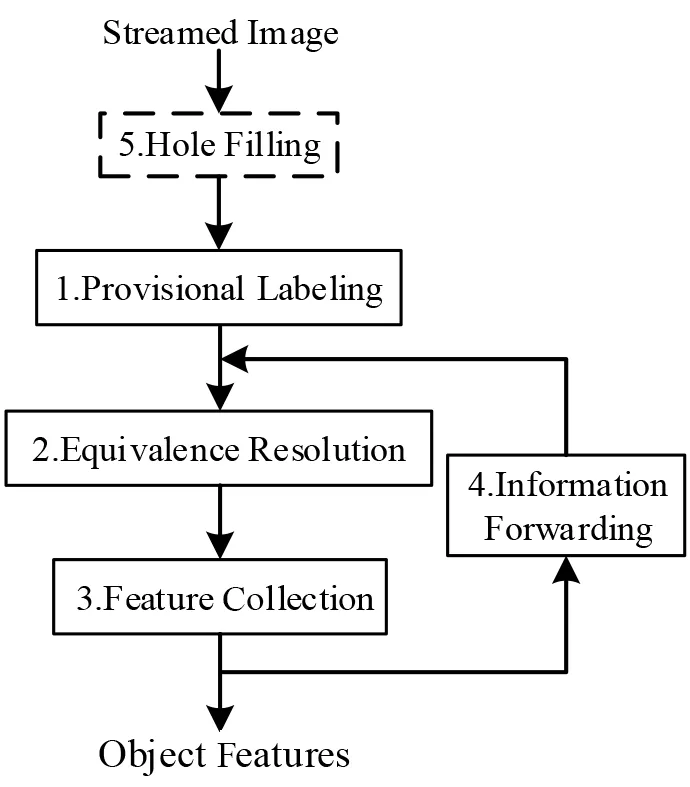
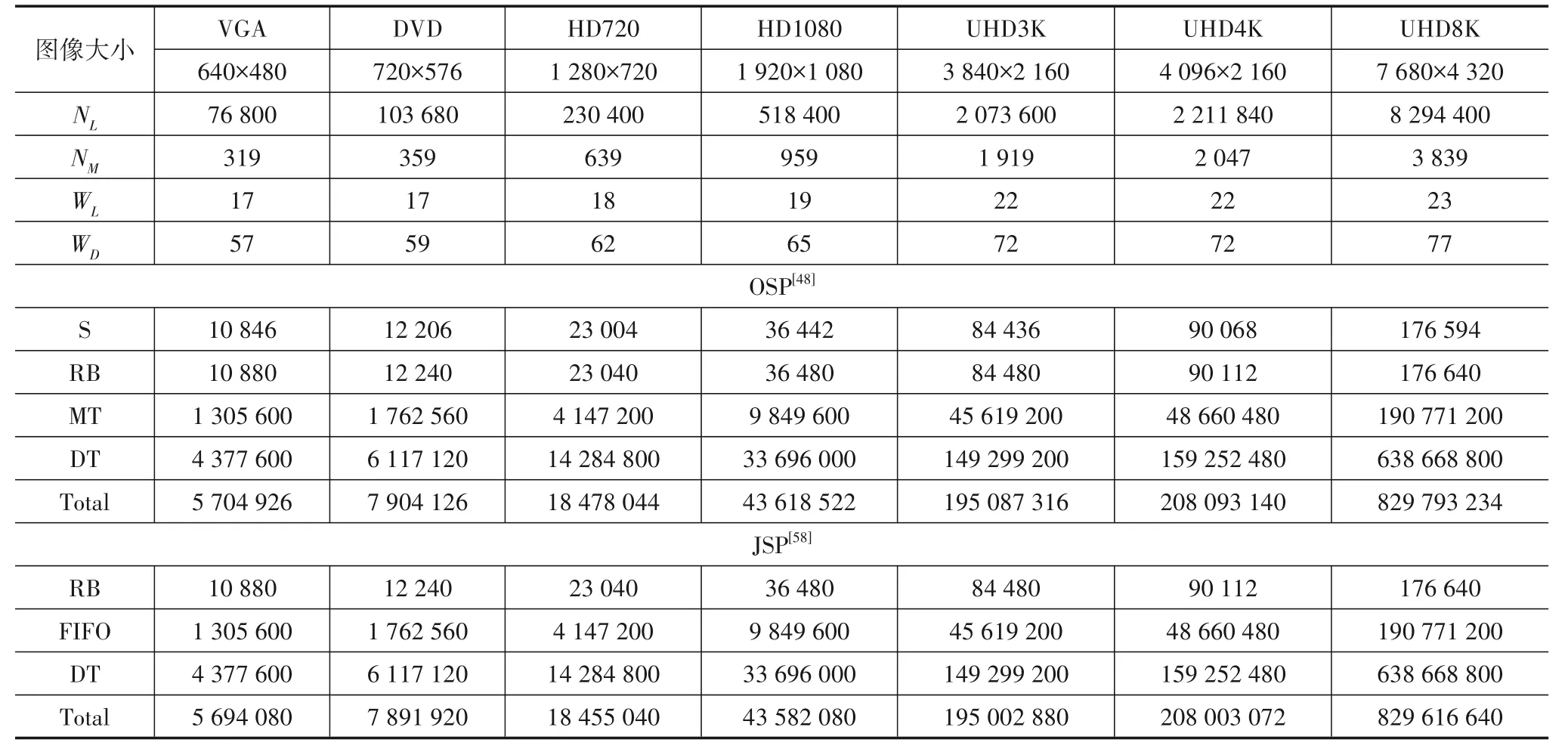
算法1 基于上下文的联合查找算法1234567891 0 11 12 13 14 15 16 17 18 19 20 21 22 Newtree(node n)T[n]=n END OF Newtree Find(node n)RETURN T[n]END OF Find Union(node u,node v)e=Find(node u)f=Find(node v)IF e 图3 CCL和CCA算法的扫描窗口 为了减少内存需求,Haralick 等人[13]提出一种多次扫描算法,该算法根据邻域像素信息对二值图像进行交替地向前扫描(图3(a))和向后扫描(图3(b)),在交替扫描中处理标签等价关系,不需要等价表和额外内存空间. 交替扫描图像使得算法扫描次数不固定,连通域几何形状越复杂,扫描次数越多.Suzuki 等人[14]提出的SCL(Suzuki’s Connected-component Labeling)算法对Haralick 等人的算法做出了改进,采用标签连接表记录和处理标签等价关系.SCL 算法也需要多次扫描,作者证明最大扫描次数为4次,算法执行时间与图像连通域中的像素数成正比. Chang等人[15]提出的算法采用了完全不同的方法,通过轮廓跟踪(Contour Tracing,CT)技术标记连通域.CT算法从上到下、从左到右逐行扫描二值图像,当遇到一个连通域的外部轮廓或内部轮廓时,采用轮廓跟踪技术给轮廓上所有对象像素分配相同的标签,执行轮廓跟踪的同时也标记与轮廓相连的背景像素以保证轮廓只会被跟踪一次. 标记完连通域外部轮廓之后,整个连通域的标签就确定了,给连通域内部像素分配的标签都与外部轮廓标签相同. 作者已经证明CT 算法时间复杂度与图像大小呈线性关系. He 等人[22]提出的基于配置转换的标记算法(Con⁃figuration Transition-based Connected component Label⁃ing,CTCL)采用如图4(a)所示的扫描窗口一次性处理两个像素,通过考虑扫描窗口中像素的9 种配置的转换,尽可能多地利用处理后两个像素时检测到的信息处理当前两个像素,使在第一次扫描中要检查的像素平均数目减少,从而加快算法处理速度.Zhao等人[23]提出的ICTCL(Improved CTCL)算法对CTCL 算法做出改进,进一步减少处理像素要检查的像素平均数目,采用如图4(b)所示的扫描窗口一次处理三个像素,考虑的配置有16种.CTCL算法和ICTCL算法都采用等价标签集(Equivalent Label Set)策略记录和解析标签等价关系. 文献[35]已经证明这两种算法的时间复杂度都与图像大小呈线性关系. 本文不介绍等价标签集策略,相关细节参考文献[22,23]. 图4 CTCL和ICTCL算法的扫描窗口 He 等人[24]提出的基于游程的一次半扫描算法(Run-based Connected-component Labeling,RCL)采用等价标签集策略记录和解析标签等价关系.RCL 算法把一个游程视为一个超级像素,在第一次扫描中给每个游程而不是给游程中的像素分配临时标签. 由于第一次扫描记录了所有游程数据,第二次扫描只需重新扫描对象像素而不用扫描背景像素,故作者称算法为一次半扫描算法. 一般图片中游程数量比对象像素数量少得多,采用基于游程的技术将大大减少分配标签的成本.RCL 算法时间复杂度与图像大小呈线性关系,虽然作者声称该算法是一次半扫描,但是实质上还是两次扫描算法. Grana 等人[26]提出的基于像素块的两次扫描标记算法(Block-based Connected-component Labeling,BCL)采用等价标签集策略记录和解析等价标签. 由于一个2×2 的块内所有像素必定属于同一连通域,BCL 算法把基于像素的标签处理扩展到块上,将如图3(a)所示的扫描窗口中的像素替换成2×2的块,扩展后可以一次实现对20 个像素的连通关系分析.BCL 算法在第一次扫描中给像素块分配临时标签并记录块之间的等价关系,在第二次扫描中把块的代表标签分配给块中每个对象像素. BCL 算法时间复杂度与图像大小呈线性关系. CCL 在处理图像时需要两次扫描,第一次扫描分配临时标签,第二次扫描重新标记,并生成一个和图像同样大的标记图像. 图像分析中最重要的是连通域的特征数据提取,标记图像本质上只是一个辅助图像数据结构. 如果在第一次扫描中直接提取特征数据,那么第二次扫描就可以省去,两次扫描就可以减少到单次扫描. 在单次扫描图像的同时提取特征数据并动态地解决数据关联问题,这是近十年来研究发展的单次扫描CCA 算法的原理.CCA 算法可以处理位流图像,且不需要储存标签图像,只需要少量内存,这些特性使它们适合在FPGA 上实现,完成图像实时高速处理,因此单次扫描CCA 算法都是基于FPGA 硬件架构设计的. 基于像素的单次扫描CCA 算法处理图像时考虑像素之间的连接关系,本节分析以下几种CCA算法: (1)原始的单次扫描(Original Single Pass,OSP)CCA算法[42]; (2)改进的OSP(Improved OSP,IOSP)CCA算法[45]; (3)单次查找单次扫描(Single Lookup Single Pass,SLSP)CCA算法[48]; (4)双重查找单次扫描(Double Lookup Single Pass,DLSP)CCA算法[50]; (5)“Z”字形单次扫描(Zig-Zag Single Pass,ZZSP)CCA算法[51]. 4.1.1 OSP算法 Bailey 等人[42]提出的OSP 算法采用基于上下文的联合查找算法记录和解析标签等价关系,它并不回收标签,分配标签的顺序按照标签数值由小到大排序,因此不引入年龄平衡策略.OSP算法的硬件架构如图5所示,主要包含邻域标签处理模块、标签选择模块、合并控制和合并表模块以及数据表模块,行缓冲区只缓存一行图像像素. 图5 OSP算法的架构 OSP 算法的扫描窗口和标签选择策略与OCL 算法相同,由邻域标签处理模块给扫描窗口提供邻域标签LA,LB,LC和LD,标签选择模块根据邻域标签信息给当前像素分配标签LX,同时数据表累加连通域的特征数据.为了减少对内存访问次数,邻域标签更新采用标签传播方法,执行步骤如算法2 所示,其中添加符号“'”的标签表示上一时钟周期的标签. 算法2 标签传播12345678 LA=LB'LD=LX'IF B&D THEN LB=LX'ELSE LB=LC'END IF LC=Find(C) 当发生标签合并时,合并控制器控制合并表记录合并操作中生成的标签等价关系. 如图6(a)所示的传播合并模式生成的标签等价关系可以直接记录在合并表中,因为较大标签在合并之后不再出现(链的长度总是为1),不会影响后续标记结果. 而如图6(b)所示的非传播合并模式会形成一条长标签链,被称为链式效应[54]. 对于非传播合并模式,必须把两个合并标签记录在一个链堆栈中,在行尾展平操作中解析标签等价关系该操作被(称为解链). 图6 两种合并模式 OSP算法时间复杂度与图像大小呈线性关系,数据表和合并表大小与标签数量成正比,储存合并标签的链堆栈大小与图像宽度W成正比. 4.1.2 SLSP算法 OSP 算法的标签数量很多,与标签数量相关的结构占用了大量内存空间,为了减少内存需求,回收标签方法被提出. Ma 等人[45]发现一行像素中标签数量最多为图像宽度的一半,把标签数量压缩到这样大小可以节省可观的内存.Ma 在IOSP 算法中采用了激进的重标记方法实现了这一点,在图像每一行开头采用标签0 重新标记图像,使得标签数目最大为W/2,这种重标记技术需要一个转换表转换两行标签的连接关系. Klaiber 等人[48]提出的SLSP 算法采用一种新的标签回收方法改进了OSP 算法,基于硬件实现的算法如算法3 所示,对每个像素执行标签传播(Label Propa⁃gate)、更新数据结构(Update Data Structure)和解析过期标签(Resolve Stale Labels)三个操作,在一行像素行尾执行展平操作. 采用标签回收策略后,更新数据结构具体操作如算法4所示. 算法3 SLSP算法12345678 FOR y=0 TO H-1 DO FOR x=0 TO W-1 DO Label Propagate Update Data Structure Resolve Stale Labels END FOR Flatten END FOR算法4 更新数据结构1234567891 0 11 12 13 14 15 16 17 18 19 20 21 22 IF X THEN IF!A&!B&!C&!D THEN△New label LX=Newtree V[LX]=TRUE ELSE△label merge IF(A|D)&C&(LA or D ≠LC)THEN LX=Union(LA or D,LC)IF V[Max(LA or D,LC)]THEN Max(LA or D,LC)to reuse END IF V[Max(LA or D,LC)]=FALSE ELSE△label copy LX=LabelCopy(LA or D,LB,LC)END IF IF!V[LX]THEN Push(LX)to SLS END IF END IF AT[LX]=Y ELSE LX=0 END IF 当连通域的所有像素都被标签标记,我们称连通域标记完成,标记标签在后续扫描中不会再出现,这种标签可以回收重利用.SLSP 算法的标签回收策略采用活动标签AT(Active Tag)关联每个标签,在每一行动态地检查连通域是否标记完成,通过回收标签减少标签数量. 重用标签打乱了标签排列顺序,因此算法中引入增强标签(Augmented label)实现年龄平衡策略,增强标签由行号L·rw 与索引L·index 组成,如图6 所示的两种合并模式可以通过式(2)评估,其中LAorD表示LA或LD. OSP 算法在行尾解链使联合查找树的高度不大于1,但在下一行中高度为1 的树和另一棵树合并将有可能产生高度为2 的树. 在行尾之前,如果再次遇到树的叶结点(等级为2),进行一次查找将无法访问到树的根标签,这种叶结点对应的标签称为过期标签. 算法设置一个有效性标记V(Valid tag)跟踪标签是否为过期标签,过期标签将记录在过期标签堆栈SLS(Stale Label Stack)中,随后在解析过期标签操作中处理. 当过期标签被分配给当前像素时,特征数据将无法累加到正确的标签上,需要先把特征数据暂存起来,等过期标签的根标签进入邻域时再将特征数据累加到根标签上. SLSP 算法的时间复杂度与图像大小呈线性关系,数据表、合并表和链堆栈大小都与图像宽度W成正比. 4.1.3 DLSP算法 处理过期标签需要额外的操作步骤,这导致算法复杂度变高,处理速度变慢.Klaiber 等人[50]提出DLSP算法,采用双重查找消除了过期标签,并证明双重查找一定会找到根标签,这样消除了和过期标签相关的任何操作,降低了算法复杂度,算法实现如算法5所示. DLSP 算法以像素为扫描单元,以游程为标记单元,把基于像素的处理与基于游程的处理统一起来,进一步降低了算法计算复杂度. 同一游程的所有像素都有相同根标签,因此只需要对游程中第一个像素进行双重查找就可以找到整个游程的根标签,后续像素标签只需要传递而无需再次查找. 算法5 DLSP算法1234567 FOR y=0 TO H-1 DO FOR x=0 TO W-1 DO Label Propagate Update Data Structure END FOR Flatten END FOR DLSP 算法时间复杂度与图像大小呈线性关系,在存储空间上与SLSP算法相比减少了过期标签相关的数据结构. 4.1.4 ZZSP算法 DLSP 算法仍然存在链式效应,需要消耗额外的时钟解析标签链,Bailey 等人[51]提出的ZZSP 算法解决了这个问题. ZZSP 算法采用了“Z”字形(Zig-Zag)扫描替换光栅式扫描,交替采用如图3(a)和图3(c)所示的扫描窗口每隔一行以相反方向扫描,在下一行扫描中动态解析链式效应,也消除了行尾的展平操作. ZZSP 算法实现如算法6 所示,对每个像素只需执行标签传播(Label Propagate)和更新数据结构(Update Data Struc⁃ture)两个操作. 当扫描从行尾进入到下一行行首时,需要翻转窗口以调整扫描顺序,操作步骤如算法6 中第5~7行所示. 算法6 ZZSP算法1234567891 0 Line=FALSE FOR y=0 TO H-1 DO FOR x=0 TO W-1 IF y=even ELSE x=W-1 to 0 DO IF Line THEN 11 12 13 14 15 LA or D=0 LB=LX LC=LD Line=FALSE ELSE Label Propagate END IF Updata Data Structure END FOR Line=TRUE END FOR 与年龄平衡策略类似,ZZSP 算法依据扫描顺序定义两个像素之间的优先级关系,如式(3)所示: 其中P1 在SLSP 和DLSP 算法中,活动标签AT 只记录与标签相关的行号,而ZZSP 算法在数据表DT(Data Table)中引入AT,记录与每个标签相关的坐标,如式(4)所示: 当扫描窗口通过该坐标,即确定该标签对应连通域已经标记完成时,标签将回收重利用. 在标签复制和合并操作中,活动标签会跟随数据表一起更新,活动标签的更新将遵循公式(3)的优先级定义,对于两个活动标签AT1和AT2,当AT1的优先级高于AT2时,将会保留AT2,反之保留AT1. ZZSP 算法时间复杂度与图像大小呈线性关系,它需要额外的数据结构实现扫描顺序的转换. 一行连续连接的对象像素被称为游程,这些像素必定有相同标签. 基于游程技术处理图像,可以显著减少标签总数,有效降低解析标签等价关系的复杂度,加快算法处理速度. 基于游程的算法把游程视作一个超级像素,不再检测像素之间的连接关系,而是考虑游程之间的连接关系. Trein 等人[52]提出基于游程长度编码(Trein’s Run Length Encoding,TRLE)的CCA 算法,采用游程压缩图像,仅采用开始和结束位置描述每个游程,在一个时钟周期内只需要发送两个位置就可以代表游程中所有对象像素,加快了算法处理速度. 算法为每个游程分配一个临时标签,通过比较相邻行之间的游程关系确定标签等价关系. 为了正确解析一些复杂图像带来的合并标签等价关系,作者使用一个从旧标签指向新标签的指针,当试图更新旧标签的特征数据时,会因为指针指向新标签而最终把特征数据累加更新到新标签上. Zhao 等人[53]提出了基于游程单次扫描(Zhao’s Run-based Single Pass,ZRSP)的CCA 算法,在实时自动目标识别系统上实现了对位流图像数据的处理. 该算法以像素为扫描单元,以游程为标记单元,结合了像素和游程的优点,并设计多层索引结构保持相邻行之间标签的正确对应关系,但是在某些更复杂的图像中,仍然存在链式问题. 4.2.1 TRSP算法 Tang 等人[54]提出的TRSP 算法采用如图3(d)所示的扫描窗口标记游程,并基于链表(Linked list)结构解析标签等价关系,消除了链式效应. 为了降低内存需求,算法采用了简单且高效的标签回收策略,给游程分配的标签从0 到W/2(W为图像宽度),当标签到达最大值(W/2)时重新从0 计数. 这种自动回收标签技术无需额外的数据结构跟踪标签,也无需额外的控制逻辑判断连通域是否标记完成,减少了算法的内存空间消耗并降低了算法计算复杂度. 算法实现过程如图7 所示:首先为游程分配临时标签,再基于链表结构建立游程标签等价关系,然后根据标签等价关系计算对象特征数据,最后在标签失效前通过链表传递标签等价关系和特征数据. 图像填充过程为原始图像填充额外对象像素,是个可选过程. 图7 TRSP算法概述 TRSP 算法引入Next,Head,Tail和Data 四个表建立链表结构,其中Head 和Next 是主表,Tail 和Data 是次表,次表只能由主表Head 索引. Data 表存储连通域特征值数据,Head,Tail 和Next 表充当指针构建并处理标签等价关系. 其中Head 和Tail 指针将记录前一行的游程标签,在后续扫描中通过指针的转换实现游程标签转换,表示两行游程的标签等价.Next 指针可以在游程列表中插入新标签,将新标签附加到游程列表末尾以表示标签等价. 图8 的示例说明指针的用法,图中前一行有标签Lp,当前行有等效游程列表L1→L2→L3,假设它们属于同一个连通域,有以下定义: 图8 Next,Head和Tail指针的用法 (1)前一行标签的Head 表示当前行等效游程列表的第一个元素,有Head[Lp]=L1; (2)标签的Tail 是等效游程列表的最后一个元素,有Tail[L1]=L3,也等价于Tail[Head[Lp]]=L3; (3)Next 指向游程列表中下一个元素,对于当前行等效游程列表,有Next[L1]=L2,Next[L2]=L3. 采用这种链表结构,只需对Head,Tail 和Next 表进行单次写入即可完成标签等价关系解析,完全避免了链式效应,实现了最大的吞吐量. 本节主要分析两种算法:(1)Gu 等人[56]提出的基于单元单次扫描(Cell-based Single Pass,CSP)的CCA 算法;(2)Jeong 等人[58]提出的单次扫描(Jeong’s Single Pass,JSP)CCA算法. 4.3.1 CSP算法 CSP 算法采用单元(Cell)压缩图像,与BCL[26]算法有相似之处,BCL算法采用2×2大小的块替换像素,CSP算法的单元大小为n×n,并不局限于2×2. 对于每一个单元,只要单元中存在对象像素,那么整个单元就可以看成一个对象单元,当单元被分配标签后,单元中所有像素(无论是否为对象像素)都会获得相同标签. 当N=nM时,CSP 算法把N×N大小的像素图像压缩成M×M大小的单元图像.CSP 算法只考虑四连通性,假设b(x,y)表示坐标(x,y)的单元,其中0≤x≤M-1,0≤y≤M-1,当前单元b(x,y)对应标签表示为LX,它上方单元b(x,y-1)对应标签表示为Lup,它左边单元b(x-1,y)对应标签表示为Lleft,为当前单元选择标签如算法7所示. 算法7 CSP算法1234567891 0 11 IF b(x,y-1)=b(x-1,y)=0 THEN LX=Lnew ELSE IF b(x,y-1)=1,b(x-1,y)=0 THEN LX=Lup ELSE IF b(x,y-1)=0,b(x-1,y)=1 THEN LX=Lleft ELSE IF b(x,y-1)=b(x-1,y)=1,Lup=Lleft THEN LX=Lleft ELSE b(x,y-1)=b(x-1,y)=1,Lup ≠Lleft LX=Min(Lup,Lleft)END IF CSP 算法采用重标记存储器(Relabeling Memory)记录和解析标签等价关系,在每行行尾根据记录结果从右到左将临时标签替换成新标签进行重新标记. 当n=1时,CSP算法与基于像素的CCA 算法有相同结果,当n> 1 时,两者的结果将并不完全一致,因为CSP 算法中被认为相互连接的对象单元中可能有并不相连的像素. 这是考虑算法计算复杂度和结果精确度之间的结果. 当n>1时,CSP算法的计算复杂度和内存消耗从O(N2)降低到O(M2). 4.3.2 JSP算法 为了消除链式效应,JSP 算法提出了一种无标签合并周期的硬件架构,如图9所示. 八连通检查器(8-Con⁃nectivity Checker)采用如图3(a)所示的扫描窗口,遵循OCL 算法的标签选择策略为当前像素选择标签;信息提取器(Information Extractor)为标记连通域累加更新特征数据;标签堆栈(Label Stack)用来管理和回收标签,新分配标签从堆栈头部弹出,回收标签存放在堆栈尾部. 标签移位寄存器在合并发生后的下个时钟周期里把所有旧标签直接替换成新标签,因此无需解析标签等价关系. 图9 JSP算法的硬件架构,其中红线表示S1的输入和输出 该架构采用标签移位寄存器替换行缓冲区储存标签信息,相邻标签移位寄存器之间有一个条件选择器S1,S1的输入、输出在图9中用红色标出. 标签移位寄存器中储存的标签在每个时钟周期向左移动,作为条件选择器输入标签LS. 八连通检查器根据扫描窗口为当前像素分配标签并储存在标签移位寄存器R0中,同时生成event 信号和输入标签Lmax,Lmin. 条件选择器在event 信号控制下,动态地从三个输入标签中选择输出标签到下一个标签移位寄存器. 发生合并事件时,event 信号输出1,合并中较大标签指定为Lmax,较小标签指定为Lmin,将它们输入到条件选择器中,对LS与Lmax进行比较,如果相同说明LS是旧标签,输出Lmin,不相同则输出LS. 对于非合并事件,event信号输出0,标签LS在移位时不改变. 本节对上述几种CCA 算法进行评估,这些算法都在它们提出的相应硬件架构中实现,在下文中提到算法简称即代表其硬件架构. 对于不同分辨率图像,CCA硬件架构的内存消耗大小是评价该架构实现位流图像处理的重要指标之一. 因此本文将从内存消耗和最坏情况吞吐量等方面分析这些算法,并比较它们的硬件架构性能. 这些算法数据都是根据它们报告的结果近似计算的,但不失一般性. 表2 比较了OSP[42],IOSP[45],SLSP[48],DLSP[50],ZZSP[51],TRSP[54]和JSP[58]算法对W×H大小图像的内存需求;表3 比较了OSP 和JSP 算法对不同分辨率图像的数据存储所需内存位数;图10 比较了IOSP,SLSP,DLSP,ZZSP 和TRSP 算法对不同分辨率图像的内存总数. 图10 几种CCA算法处理不同分辨率图像的内存位数比较 表2中为了进行公平的比较,假设所有算法都是对W×H像素大小图像进行处理,提取特征数据包括面积(Area)和边界框(Bounding box). 标签数量NL是所有架构的关键因素,它直接决定了存储器的深度和宽度. 标签重用FIFO 储存所有标签,它的大小为标签数量NL乘以标签宽度WL,标签宽度由WL=log2NL计算得到. 行缓冲区RB(Row Buffer)缓存一行像素的临时标签,它的大小为W×WL. 合并表MT记录标签之间的等价关系,它的深度为标签数量NL,宽度为标签宽度WL,大小为NL×WL. 数据表DT 储存标签对应连通域的特征数据,数据表深度为标签数量NL,宽度为特征数据宽度WD,大小为NL×WD. 由于提取的特征数据包括面积和边界框,可以计算出特征数据宽度为WD=2 log2W+2 log2H+log2WH. 表2 不同单次扫描CCA架构对于W×H大小图像的内存需求 OSP算法不回收标签,对标签的计数只需简单的计数器而不采用FIFO 寄存器,因此标签数量取决于图像大小,最大数目为WH/4.OSP 算法在行尾进行反向解链,需要一个链堆栈S 记录两个合并标签,因此链堆栈宽度为标签宽度的两倍,深度为一行图像中存在的最大标签合并次数NM=(W-1)/ 2,链堆栈大小为2×WL×NM. 由于不考虑标签回收,OSP 算法的标签数量比其他算法大的多,对应的合并表和数据表内存占用也就很大,它的内存位数量如表3所示. JSP 算法采用标签移位寄存器实现行缓冲区,通过条件选择器直接替换所有旧标签,无需解析标签等价关系. 根据文献[58]的报告,JSP 算法虽然采用了标签回收技术,但只是回收合并中的较大标签,标签回收策略并不完整,使得标签数量可能与OSP算法一样大. 如表3所示,JSP 算法的标签重用FIFO 和OSP 算法的合并表一样大,但OSP算法还需要一个链堆栈S记录合并标签,所以内存需求上OSP 算法更大一些. 对比表3 和图10 可以发现,这两种算法的内存需求远远大于其他算法(800M 对比900K),OSP 算法内存需求是所有算法框架中最大的,JSP算法次之. IOSP 算法采用激进的重标记方法使标签数量减少到W/2,但这种重标记技术额外需要一个深度为NL,宽度为WL的转换表TT(Translation Table)管理上一行和当前行标签之间的关系,此外,还需要两个合并表和数据表分别记录两行标签和特征数据. 如表3 和图10 所示,IOSP 算法与OSP 算法相比显著减少了内存需求,但在图10所示的算法中,IOSP算法内存需求仍是最大的. 表3 OSP和JSP算法架构对不同分辨率图像的内存需求比较 SLSP算法通过回收标签使标签数量NL依赖图像宽度W,额外的5个时钟周期延迟用于补偿标签回收处理操作. 增强标签使用行号扩展了标签宽度,变为WAL=WL+log2H. 算法的标签回收策略采用标签重用FIFO 寄存器管理标签,需要增加一个两位比特的活动标签AT跟踪连通域标记是否完成,还需要一个一位比特的有效性标记V 跟踪标签是否为过期标签,过期标签储存放在过期标签堆栈SLS 中. 算法中证明过期标签的最大数量为W/ 10[48],即SLS 深度也为W/ 10. 与IOSP 算法相比,SLSP算法只需要一个合并表和数据表,由于标签宽度变宽,合并表内存大小几乎相同,但数据表内存缩小一半,总内存需求显著减少了约28%. DLSP 算法通过双重查找解决了过期标签问题,无需过期标签堆栈SLS 和有效性标记V,进一步减少内存需求,但这两个辅助数据结构内存消耗都比较小,因此提升有限,内存需求只减少约2%. ZZSP 算法需要额外的储存器结构实现“Z”字形顺序扫描,在扫描期间动态解析标签等价关系,避免了链堆栈S 的需要. 算法中采用更大的活动标签AT 记录横坐标x(最大为图像宽度W)和纵坐标y的最低有效位(一位比特). 与DLSP算法相比内存量减少了约6%. TRSP 算法采用了两个行缓冲区,但行缓冲区不储存临时标签,宽度仅为一比特. 算法中还采用了4 个表,每个表的深度最大为NL,由Head,Next 和Tail 表组成的链表结构替换合并表解析标签等价关系,表位宽为WL,Data 表位宽为WD. 算法采用的标签回收技术避免了标签重用FIFO和活动标签AT的需要,有效减少内存需求,与SLSP 算法相比减少了大约30%,与ZZSP 算法比减少了大约25%. 表4 比较了OSP[42],IOSP[45],SLSP[48],ZZSP[51],TRSP[54]以及JSP[58]硬件架构的实现结果,由于各种架构实现FPGA 技术不同、处理图像分辨率不同和提取特征参数不同,为了实现公平比较,比较结果只包括CCA硬件架构,不考虑图像采集和外部接口模块. 为了分析不同架构的性能差异,采用如公式(5)所示的线性函数对原始数据进行归一化处理: 表4 几种CCA硬件架构的比较 其中X为原始数据,Xmax和Xmin为原始数据中最大值和最小值. 由于LUT(逻辑查找表)和寄存器都是由FPGA 内部逻辑查找表综合生成,所以衡量FPGA 寄存器资源消耗可以将二者累加综合考虑. 归一化结果在LUT、寄存器和BRAM方面越小越好,最大工作时钟频率越大越好. 在处理256×256 分辨率图像时,SLSP 架构消耗了最多BRAM,归一化结果为1.0,LUT 和寄存器消耗为0.09,最大工作时钟频率为0.7. ZZSP 架构采用LUT 作为分布式RAM 实现小型数据结构需要消耗更多LUT,但显著减少了BRAM,此外,它的最大工作时钟频率也是最高的,各项性能(LUT,BRAM 和最大工作时钟频率)归一化结果分别为1.0,0.0 和1.0.TRSP 架构采用简化逻辑的链表结构构建标签等价关系,只需要很少的寄存器和LUT 资源,但是最大工作时钟频率最低,它的各项性能归一化结果为0.0,0.6和0.0. 在这三种算法架构中,ZZSP 架构不仅有最少的BRAM 和最高的最大工作时钟频率,且在寄存器资源消耗上也不多,综合性能是最优的. 在处理640×480 分辨率图像时,OSP 架构消耗较少硬件资源是因为处理图像中仅包含255 个标签,消耗LUT 和BRAM 的归一化结果为0.006 和0.0. IOSP 架构需要两个合并表和数据表记录标签等价信息和数据信息,使得LUT 和寄存器单元消耗较OSP 架构翻了一倍,它的各项性能(LUT,BRAM 和最大工作时钟频率)归一化结果为0.04,0.737和0.0.JSP 架构为了在合并期间替换所有旧标签,采用标签移位寄存器和多路选择器实现标签更新,多路选择器通过逻辑运算输出标签,导致架构消耗的LUT 资源远远大于其他架构,并降低最大工作时钟频率,它的各项性能归一化结果为1.0,0.026和0.353.TRSP架构在四种架构中消耗最少的寄存器资源并有最高的最大工作时钟频率,各项性能归一化结果为0.0,1.0 和1.0. 虽然TRSP 架构也消耗了最多的BRAM,但是综合性能超过了其他三种架构. 综合上述分析,ZZSP 架构的综合性能是所有架构中最优的. 架构的吞吐量分为两部分:一部分为每个时钟周期处理一个像素的静态部分,这使得算法的吞吐量直接受限于硬件架构工作时钟频率;另一部分为根据图像内容解析等价关系的数据相关部分,这将会影响架构处理单个像素的平均周期. 各架构在最差情况下处理像素的平均周期最大,决定了处理时间的上限,因此比较最差情况下架构的吞吐量有一定意义. 图11 给出了CCA 算法对应最差吞吐量图案. 如图11(a)所示的阶梯图案将会产生最大的链堆栈,OSP[42],SLSP[48]和DLSP[50]架构在行尾解链会额外增加W/5 个时钟周期消耗,这些架构处理一个像素需要6/5个时钟周期. IOSP[45]架构中许多合并是由转换表决定的,使得创建最大链堆栈的模式变得更加复杂,如图11(b)所示的羽毛图案中两行像素增加W/ 8 个时钟周期消耗,IOSP架构处理一个像素需要17/16个时钟周期. 图11 造成最差吞吐量的图案 如图11(c)所示的棋盘图案限制了游程的优势,是所有基于游程算法的最差情况.TRSP[54]架构虽然是基于游程算法,但它和ZZSP[51]、JSP[58]架构都不需要额外时钟周期处理标签等价关系,因此它们处理一个像素只需要一个时钟周期. 如表4 所示,TRSP、JSP 和ZZSP架构的吞吐量和工作时钟频率相同. 优秀的处理算法不仅要实现实时处理,即需要以每个时钟周期一个像素的速度处理位流像素,还要合理使用硬件资源. 在基于像素的CCA 算法中,OSP[42],IOSP[45],SLSP[48]和DLSP[50]算法解链延迟取决于图像连通域的几何复杂度,这导致算法吞吐量不一致. 对于一般图像,解链延迟通常小于1%[51];但对于最差情况,单行延迟可达50%,整幅图像延迟为20%,使得算法无法实现实时处理. ZZSP[51]算法采用“Z”字形扫描避免解链延迟,实现了实时处理. 虽然采用“Z”字形扫描和多次查找合并表使得该算法需要比光栅式扫描算法更多的逻辑资源,但是总体资源消耗仍然较少. 因此ZZSP 算法是最优的基于像素的单次扫描CCA算法. TRSP[54]算法通过链表结构操纵指针管理标签合并实现实时处理且消耗硬件资源较少,是最优的基于游程的单次扫描CCA 算法. 然而,TRSP 算法是四连通域检测算法,在检测精度上落后于八连通的ZZSP 算法. 但四连通扩展为八连通并不困难,因此TRSP 算法仍然是较优的CCA算法. JSP[58]算法也可以实现实时处理,但是与上述算法不同,它采用标签移位寄存器结构进行数据存储消耗了大量逻辑资源并导致时钟频率较低,此外,算法中回收标签不完整,导致内存需求很大,这使得JSP 算法的性能与ZSSP和TRSP算法相比相差较大. 本文分析了近十年以来国内外发展的CCL 算法和CCA 算法,介绍了主要CCA 算法的实现策略和架构,还介绍了适合CCA 算法的等价解析策略,并比较了几种主要算法的内存需求、硬件架构和延迟. 在内存方面,OSP 和JSP 算法的内存需求远大于其他算法,TRSP 算法的内存需求最小;在硬件架构方面,ZZSP 算法实现了最大的工作时钟频率;在延迟方面,ZZSP,TRSP 和JSP 算法的每秒吞吐量和时钟频率相同,都可以实现实时处理. 综上所述,ZZSP 和TRSP 算法是最优的单次算法CCA 算法. 本文分析结论为实现基于FPGA 高速位流图像的连通域检测提供了理论依据和数据参考. 关于CCA 问题的相关工作,未来可以从以下几个方面进一步展开: (1)寻找更加有效的标签等价关系解析方法,当前联合查找算法中的展平操作中会增加延迟,如果能够在扫描过程中直接解析等价关系而不用等到行尾,那么就可以减少延迟,提高算法处理速度. (2)在多块FPGA 上并行实现CCA 算法,进一步提高基于硬件架构的CCA算法处理速度. (3)对现有CCA 算法和硬件架构进一步改进和融合,使其能够更有效地提取图像中连通域特征. (4)在当前CCA 算法中,提取连通域的特征只包括面积、边界框和质心,设计新的CCA 算法提取图像的周长、圆度和欧拉数等更多特征. (5)设计适用于超大分辨率图像的处理算法,可以考虑将超大图像分割成多块,对分割的多块子图像进行标记处理. (6)可以结合现代工业对三维图像检测的需要,将CCA 算法的设计从二值图像处理扩展到三维图像处理. 通过研究分析三维图像像素之间的连通关系,实现对三维图像的CCA算法的高效并行化实现.

4 连通域分析
4.1 基于像素的单次扫描CCA算法






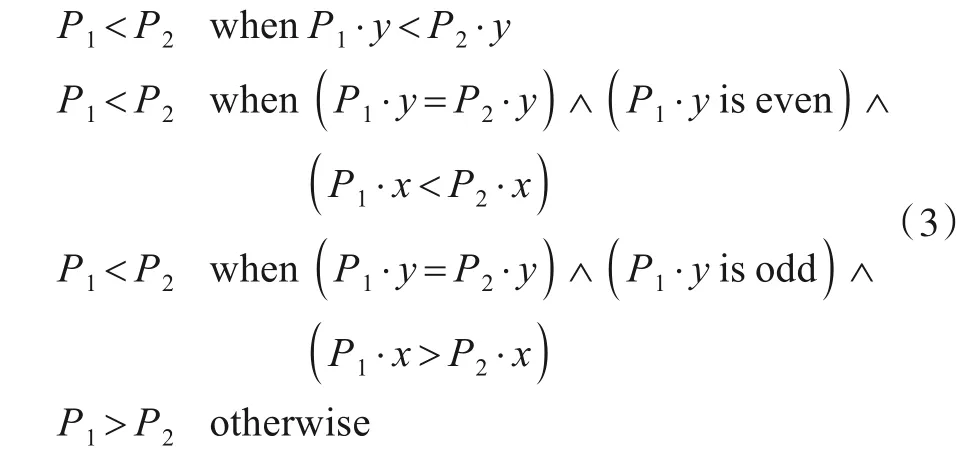

4.2 基于游程的单次扫描CCA算法

4.3 其它单次扫描CCA算法


5 比较与分析
5.1 内存需求分析


5.2 硬件架构比较


5.3 最差情况吞吐量

5.4 综合分析
6 结论与展望

