一种卷积自编码深度学习的空气污染多站点联合预测模型

张 波，陆云杰，秦东明，邹国建

（1. 上海师范大学信息与机电工程学院，上海 200234；2. 同济大学电子与信息工程学院，上海 201804；3. 上海智能教育大数据工程技术研究中心，上海 200234；4. 中科三清科技有限公司，北京 100089）

1 引言

城市空气污染问题日趋严重，已经给人们的身体健康［1］以及日常生活造成了严重的影响［2］，相关环境部门以及研究人员对空气质量问题的关注度越来越高［3］.随着信息技术的飞速发展，空气污染预测问题也迎来了全新的研究思维. 利用大数据思维与深度学习技术的结合对空气污染进行有效的数据分析，进而做出准确的预测是当前环境科学和计算机科学交叉学科研究的前沿热点问题［4～6］.

目前，城市空气污染预测主要通过部署多个污染监测站点进行数据监测，然后采用综合数据分析等方法开展. 一般来说，数据分析预测，如概率模型法、机器学习方法等，都在这类问题中有广泛的应用，这些研究方法各有特点，如朴素贝叶斯［7］、BP（Back-Propagation）神经网络［8］等都能在一定规模的数据集下取得比较好的预测效果. 但是这些方法还有一些不足，比如，模型结构及获取的特征较单一，其计算模式适应特定城市条件而缺乏泛化能力；同时，由于站点分布地理位置不均，站点数据之间的地理空间关联特征未获得挖掘，无法充分提取多站点的污染物及气象大数据之间的时序以及空间关联性的问题，使得预测不够精确. 因此传统的预测方法仍存在各自的瓶颈有待突破［9～11］.

近年来，深度学习方法在各个领域都获得了突破，比如图像识别［12］、自然语言处理［13］、生物工程［14］以及时空结构的特征学习与分析［15］等领域，基于深度学习的城市空气污染物浓度预测也获得了相应的关注. 通过对大量数据的有效训练，深度学习可以很好地提取数据之间的时间与空间关联性，这是传统预测方法所不具备的.

卷积神经网络（Convolational Neural Network，CNN）［16，17］已经在图像领域取得了很大的成就，证明其在处理空间数据方面具有极其强大的功能. 因此，在处理分布不均匀站点间的污染物数据间的空间相关性时，CNN 能够获取多站点间的空间信息，然而仅仅使用CNN 获取到的空间信息对于解决长时间的时序预测问题是不够的. 长短期记忆网络（Long Short-Term Memo⁃rg，LSTM）［18］在时间序列数据处理方面具有优异的性能，而污染物数据也是以时间序列数据形式呈现的，所以大多数污染物预测问题使用LSTM 进行预测［19～36］. 但是单独使用LSTM 预测时考虑到时序数据间的长时间依赖关系，且其结构仅能进行单点的预测，例如根据输入的历史24 h数据，单独地预测未来25 h、26 h的数据，不能根据上一时刻的预测输出作为下一时刻的输入，做到连续的预测. 秦东明等人［21］提出的自编码网络空气污染预测模型正是基于LSTM 的，该模型的编码解码部分均由多层的LSTM 堆叠构成，并且该模型可以解决LSTM 做长时间预测时的缺点，但是该文章仅根据单城市的综合历史污染物数据来预测未来单城市的污染物浓度，没有运用在复杂的分布不均匀的多站点间的污染物浓度预测中. 现有的应用在城市空气污染预测的深度学习模型虽然能够取得一定的预测效果，但是都面临着以下几个问题：

（1）站点地理分布不均，无法提取数据间深层次的空间以及时间关联关系，从而难以实现特定地点预测水平的提升；

（2）不能同时融合时空特征，有效地连续预测未来一段时间内的污染物情况；

（3）由于模型结构以空间或时间为主，多维度数据的利用能力不足，提取数据内部关联特征能力单一，导致模型的泛化能力不足.

针对传统机器学习方法的不足，本文提出了CAELearning（Learning net based on CNN and Auto-Encoder）模型. 此前的研究大多聚焦于以单城市内的综合污染物数据来进行单城市的污染物浓度预测［21，33，34］，并未考虑城市内多个分布不均匀站点之间的时空关系特征来进行联合预测. 针对该问题，本文模型提取到城市内多个分布不均匀站点之间的污染物浓度及气象数据在空间及时间上的关联性，实现了多站点间的联合预测.CAE-Learning 从模型的串行角度考虑污染物和气象数据时空特性的耦合关系. 本文在模型的构建过程中，从多站点污染物浓度和气象数据的特性角度出发，选择合适的网络作为构建CAE-Learning 模型的重要组成部分，充分考虑了多个城市污染数据的时空关联特征，从数据和模型的角度出发进行预测. 从数据的角度，多个城市之间的数据在空间上存在着相互的关联特性，因此在污染物浓度预测的过程中应该充分考虑空间关联特征［31］；在时间维度上，污染物具有动态变化的过程［20］，且目标任务是预测未来一段时间内的污染物浓度；从模型的角度，CNN 在提取空间关联数据特征上具有巨大的优势，因此使用CNN 作为模型的底层来提取空间关联特征［37］.LSTM 的端到端模型的优势在于能处理长时间序列预测任务，因此使用基于LSTM 的端到端模型作为长时间污染物浓度序列预测的生成器，实现污染物浓度的精准预测［21］. 本文提出的新型CAELearning 污染物浓度预测模型，其使用串行的连接方式来提取多城市污染物浓度和气象数据的时空关联特征. 本文使用CAE-Learning 网络结构来做多城市污染物浓度和气象数据的时空特征提取器，实现目标城市未来一段时间内污染物浓度的精准预测.

根据数据的特性，构建CNN和基于LSTM端到端模型的CAE-Learning. 首先，针对多站点的污染物浓度和气象数据的空间特征，模型采用的是多维卷积CNN 作为空间关联特征提取器. 多维卷积CNN 可以提取输入数据的空间关联特征［37］，针对具有空间特性的环境污染数据进行更深度的提取，产生高维的语义特征信息.提取后的信息作为后续的端到端模型的输入. 而基于LSTM 的端到端模型架构，其Encoder 以及Decoder 部分均由LSTM 组成. Encoder 部分结合了时间以及空间的特征，即每一个时间点，Encoder 部分的LSTM 均能提取到数据间的空间关联特性，在整个输入时间序列维度上来说，提取到的是时间和空间两个方面的特征.De⁃coder 部分根据Encoder 部分的输出和上一时刻的输入迭代完成长时间污染物浓度序列预测任务，即Decoder部分每一时刻的预测值均进行了相互的强关联［38］. 该多站点联合预测模型可以根据过去72 h 的多站点的污染物浓度以及气象数据来预测未来24 h 的特定站点的污染物浓度，实现了对未来长时间内的污染物浓度的连续精准性预测. 在测试集上的实验结果表明，提出的CAE-Learning 模型在不同城市的预测上均可以获得较高的精确度，模型具有较高的泛化性.

CAE-Learning 模型在处理空气污染预测问题时具有如下贡献：

（1）能有效地将单城市多站点间的污染物浓度和气象数据进行结合，多维卷积的CNN 能够联合多站点间的污染物浓度和气象数据特征做到深层的空间相关性提取，能够从环境污染大数据的空间关联特征角度去进一步提升预测模型的精确度，并且模型的卷积部分，采用了全卷积方法，去除了池化层带来的大幅度特征损耗问题，充分地提取污染物与气象数据的空间特征［39］.

（2）引入了端到端的编码预测模型，轻量化了基于LSTM 的自编码模型的复杂度，能够充分提取多站点间空气污染物和气象数据的时间关联性，降低了模型的过拟合问题，避免了梯度消失和梯度爆炸问题，能够从时序数据的角度进一步提升预测模型的精确度.

（3）本文使用的是新型预测模型，且综合了时空域特征问题，解决传统模型的特征提取深度不足以及特征关联度不强等问题. 模型可以将预测的污染物浓度结果进行前后关联，对未来一段时间内污染物浓度连续性预测的精确度有了很大的提升.

2 相关工作

空气污染浓度预测方法可以分为传统的非深度学习方法和基于深度学习的方法.

2.1 非深度学习方法

非深度学习方法用于空气污染浓度预测，包括基于经验模型、基于概率模型、基于传统机器学习的预测.

（1）基于经验模型的预测，根据相关数据通过归纳参数和变量之间的关系得出相应的数学关系式. 如经验统计方法［22］、回归方程法［23］. 但是在进行环境空气污染物浓度预报时，经验模型往往大量地引入历史观测数据，有很大的局限性，不符合实际情况.

（2）基于概率模型的预测，以概率统计规律为基础，结合统计学或数学的一些方法建模. 例如，用决策树模型来预测大气污染物［24］；以高斯预测概率密度函数的形式产生概率预报［25］；利用贝叶斯算法研究不同来源的污染物对其预测浓度的影响［26］；用隐半马尔可夫模型进行污染物浓度预测［27］.

（3）基于传统机器学习的预测，最早应用于环境空气污染预测领域的智能算法. 在传统的机器学习预测中，BP神经网络经常被用来做预测［28，29］，该方法能够在小规模的数据集上取得有效的预测结果，然而大规模的空气污染浓度及气象数据之间具有时间依赖以及空间相关性，而BP 神经网络无法挖掘数据间的这些深层次联系. 比起深度学习，传统机器学习不能挖掘数据中深层次的联系而无法建立更精确的预测模型.

2.2 基于深度学习的方法

深度学习方法［30］能够通过合适的训练方法对样本数据进行一系列的训练，并反向调整网络参数，最后得到具有深层次的网络结构的机器学习过程. 由于传统预测方法的不足，近年来学术界开始尝试采用深度学习方法进行城市环境空气污染预测的工作［31］. 而深度学习虽然是机器学习的一种，但是比起传统机器学习方法，深度学习方法在预测时能够充分地提取数据间的关联特征，并在此基础上建立更为精准的预测模型.目前国内外研究者已经使用深度学习方法开发出多种空气质量预测模型，如使用深度集成模型［32］进行空气质量的预测，使用扩散卷积神经网络［33］进行精确的空气质量预测，使用自编码网络［21］做空气污染物浓度变化的预测，采用深度学习进行空气质量的插值、预测、特征分析［34］，采用新型的时空长短期网络［35］进行空气污染预测.

（1）深度集成模型利用历史空气质量及气象数据以及不同的天气模式划分不同的区域，对每个区域采用深度LSTM 学习数据间的长短期依赖关系，再对每个区域得到的预测结果进行集成，得到最终的预测结果.

（2）扩散卷积神经网络在进行空气质量预测时，利用邻域特征来表示空间相关性，并构建一个图，表示监测站点之间的相似程度. 该模型根据过去数小时的空气质量、气象数据及地理环境的图像，来预测单城市的特定污染物的浓度变化.

（3）自编码网络预测空气污染物浓度变化时，根据城市内综合的历史空气污染物浓度数据，利用自编码网络的特性，使用编码器对已知时间范围内的历史污染物数据进行学习，输出一段包含历史数据特征的隐藏向量；进而使用解码器利用这段隐藏向量预测未来短期时间的污染物浓度，达到对城市内综合污染物浓度变化预测的目的.

（4）利用深度学习方法解决了空气质量的插值、预测、特征分析这三个问题，并且在实现过程中，在深度学习网络的不同层次中嵌入半监督学习，来提高插值、预测的性能，最后实验表明该模型可以在单城市的数据集里面解决上述问题.

（5）新型时空长短期网络结合了卷积神经网络及长短期记忆神经网络，在使用该网络对城市内污染物浓度进行预测时，对污染物数据进行时空特征提取后，再加入气象数据及气溶胶数据，帮助模型更好地预测空气污染物的变化.

以上基于深度学习的研究方法大多着力于解决单城市内的综合污染物数据来进行单城市的污染物浓度预测［21，33，34］，并没有考虑到城市内多个分布不均匀站点之间的空间及时间关联性对城市内单个站点的污染物浓度变化的影响，也并未做到对未来一段时间内的空气污染物浓度变化情况的连续性预测. 相比而言，本文提出的CAE-Learning模型，由CNN及基于LSTM 的自编码网络构成，突出城市内多个区域的空气污染物及气象数据联合对特定位置预测的能力，其特点在于：实现了轻量化端到端的编码预测模型［21］；避免池化层的大幅度特征损耗问题，充分地提取空间关联特征.

3 CAE-Learning空气污染预测模型

本文提出的CAE-Learning 预测模型融合了CNN 及基于多层LSTM 的自编码网络，可以有效地对城市内多站点数据间的时间、空间关联特征都做到充分的提取.由于城市内多个站点的污染物以及气象数据在空间上具有空间关联性，并且CNN 由于其模型结构，相比于其他深度学习、神经网络模型而言，其空间信息提取能力要更强，所以CNN 在提取空间关联信息上具有很强的优势［35］. 而污染物浓度在时间维度上是具有前后动态性的，是随着时间进行变化的过程. 同时LSTM 神经网络很适合于提取长时间序列的特征［39］，相较于其他模型，该模型的时序信息提取能力更强、更好. 所以根据污染物浓度的特性以及LSTM 的特点，采用LSTM 作为时序信息提取器. 而为了得到未来24 h 的污染物浓度的预测值，采用了端到端的模型架构，并且Encoder 以及Decoder 部分均采取LSTM 网络，进行有效的时序信息的提取. 相较于在之前的时空污染物浓度预测任务中取得最好预测效果的串行耦合的CNN-LSTM［37］而言，本文在提取空间信息时也采用CNN，但是在后续的时序信息获取时，为了能够更精确地根据历史多个小时多站点组成的污染物浓度数据来预测未来24 h 的特定污染物浓度预测值，采用了基于LSTM 的端到端预测模型，获得了更好的预测效果. 本节先介绍时空预测问题的建模，再介绍CAE-Learning 模型的实现及训练过程.

3.1 时空预测问题建模

本文的多站点联合预测问题主要是解决时空融合的时间序列预测问题，根据城市内多站点间空气污染物浓度及相关气象数据来对特定目标站点的污染物浓度进行预测. 如图1 所示，图1 左侧部分为多个相邻站点及目标站点之间的联合预测示意图，其中每个站点的数据特征都由污染物浓度及气象因子构成. 由多个站点及其特征组成一个二维的矩阵，根据输入的具有时空特性的二维矩阵得到输出的一个一维向量，即所要得到的时间序列预测.

图1 多站点的时空关系图

具体时空预测问题建模的数据流表示为：给定多个站点S={s1,s2,…,st,…,sn}，其中st为目标站点，其余站点为相邻站点，n为站点总数. 例如站点s1包含污染物浓度及气象数据的时间序列数据Rs1={r1,r2,…,rt,…,rk}，其中，rt为待预测的目标污染物PM2.5，w为每个站点包含的污染物浓度及气象数据特征数. 在当前多站点数据集下，数据的输入格式、输入时间间隔以及未来污染物浓度预测的时间序列的长度为：给定一个时间点t，将t之前的D小时内的数据作为历史输入数据，数据时间间隔为1 h，令T1={t-D,t-D+1,…,t}为t之前的D小时内输入到预测模型中的数据序列，用于预测之后M个小时T2={t+1,t+2,…,t+M}的目标污染物rt的浓度，预测数据的时间间隔也为1，且每个时间点的输入数据为一个n×w的二维矩阵Ii. 图2 表示由城市内多站点间的时间序列数据组成的二维矩阵数据流，作为模型的输入数据形式.

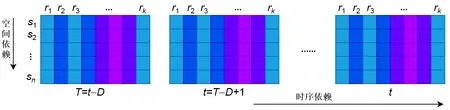
图2 输入模型的数据形式

输入数据时间间隔为1，将t之前的D小时内的数据表示为I={It-D,It-D+1,…,It}，其中I的维度为D×(n×w)，对于M小时后预测的目标污染物的浓度序列时间间隔也为1，t之后的预测序列数据表示为P={Pt+1,Pt+2,…,Pt+M}，其中P的维度为(M×1)，将CAELearning 模型表示为目标函数fCAE，可得数学模型表达式为

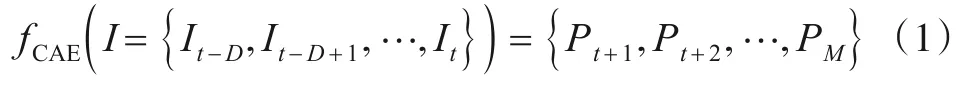
3.2 CAE-Learning预测模型

模型从空间和时间两个维度出发，设计了一种以CNN 作为底层以提取空间关联特征，基于多层LSTM 的自编码网络作为中间层以提取时间序列特征，全连接层作为顶层以产生最终预测结果的三层架构的预测模型CAE-Learning. CAE-Learning 的整体模型框架如图3所示. 首先模型的输入为时间序列D的城市内多个站点的空气污染物浓度数据和气象数据，然后数据进入具有卷积层和池化层的CNN 中进行空间关联性特征提取，将提取过的特征数据输入到自编码网络的编码器中进行时间关联特征提取，并最终将自编码网络的解码器的每个时刻隐藏状态送入到全连接层产生一个一维的预测结果，即需要的PM2.5的预测结果. 下面分别介绍CNN、自编码网络两个模型的预训练过程以及最终CAE-Learning的全局训练过程.

图3 CAE-Learning预测模型框架

（1）CNN的预训练过程

在对CNN 训练之前需要做的是对数据的预处理工作：首先对数据进行空值填充后再归一化，然后将输入污染物浓度数据和气象数据转化成CNN 可接收的具有时间序列的二维矩阵，然后再输入到CNN 中进行空间特征的提取. 本阶段的预训练是用前一时刻的污染物浓度和气象数据作为CNN 的输入，再利用全连接层接收卷积神经网络的输出并产生下一时刻的目标污染物浓度预测值. 令η为当前卷积神经网络模块正在训练的层数，m代表最终提取到的特征图，卷积层的上一层输出的特征图由该卷积层的卷积核k进行特征提取并学习，f为Relu 激活函数，通过激活函数对卷积的结果进行非线性变换而得到输出的特征图，i，j均为特征图下标，M为特征图的通道数，即

特征图经过CNN 中的卷积层卷积过后，得到N个特征图作为池化层的输入，本模型中的池化层通过平均池化方法对N个特征图进行降维，将输出N个缩小后的特征图，过程如下：

其中，β和b分别作为输出图像的相乘性质和加性偏置，down(∙)表示下采样函数，down(∙)即为平均池化方法，将这N个特征图展开成N个一维向量，再经过全连接层的解码，最后得到输出的污染物浓度值.

这一阶段输入的二维矩阵为t时刻之前D小时的多站点的污染物浓度和气象数据，以均方根误差衡量预测的准确性. 预训练过程中采用误差反向传播算法，将池化层作为考虑的因素并基于所有值更新卷积层的权重，优化网络预测性能，减少预测值和观测值之间的误差.

这一阶段的训练的主要作用就是将输入的二维矩阵进行压缩，同时深层次挖掘数据间的空间关联特征.当网络符合期望后，停止第一阶段网络的训练，将本阶段训练好的CNN 权重参数迁移到本节提出的CAELearning模型当中，然后进入第二阶段的训练.

（2）自编码网络的预训练过程

为了有效利用现有污染物浓度和气象数据来提取数据间的时序特征，并能够预测未来一段时间内的污染物浓度，本文采用了一个基于多层LSTM 的自编码网络，其解码与编码部分都由多层的LSTM 组成，LSTM 所具有的解决长时间依赖问题的能力和避免梯度消失问题的优点，可以应用这些优点来解决时序预测问题. 自编码网络的编码器部分用来提取输入序列的时间关联特征，解码器部分则将每个时刻的隐藏状态输入到全连接层产生最终的预测结果.

如图4 所示，自编码网络先由LSTM 构成的编码器部分来提取出城市空气污染物浓度和气象数据的时序特征，实现对历史污染物的浓度和气象数据的编码，然后形成一个具有时序特征的隐藏向量C，隐藏向量作为解码器端的输入，进一步做时序预测.

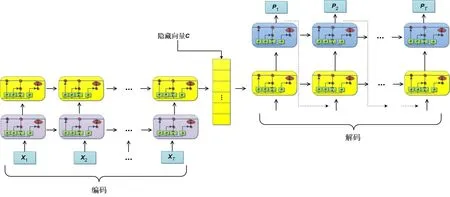
图4 自编码网络模型结构图

（a）编码器部分的设计

假设给定输入序列X=(x1,…,xt,…,xT)，则隐藏向量C为

其中，xt为t时刻的输入值；ht-1为上一个时刻长短期记忆网络输出的隐藏状态；f为LSTM 函数；ht为t时刻的隐藏状态；ρ为隐藏状态计算函数，可由式（5）得出；向量C为LSTM中的最后时刻单元的输出状态. 式（5）中，i，f，o分别表示LSTM 中的输入门、遗忘门和输出门；Ct表示神经单元的状态信息；x表示网络输入；W表示网络参数；b表示偏置量；h表示隐藏状态；σ表示sigmoid函数，输出0～1 的值，表示让多少信息通过，1 表示让所有信息都通过. 由式（4）得到的隐藏向量C会作为解码器的输入. 同样由多层LSTM 组成的解码器会将最后一层的LSTM 的隐藏状态作为整个编码器的最终输出状态，此时编码器的任务结束.

（b）解码器部分的设计

解码器主要功能是结合语境向量C和当前时刻的输入数据预测下一时刻的污染物浓度.

解码器的主要计算方法如下：

其中，f为LSTM 函数，其函数的实现形式如式（5）所示；st是当前时刻t的隐藏状态；ht-1为上一时刻的输出值；st-1为t-1 时刻的隐藏状态；C为编码器输出的语境向量；ht为t时刻输出；pt为t时刻污染物浓度的预测输出；W和b为模型参数.

在自编码网络中，编码器和解码器使用同类型LSTM 结构，一个用来编码输入序列，另一个用来解码输出序列. 其中，编码器和解码器中的LSTM 层数是可以调节的.

（c）自编码网络的预训练过程

（I）在自编码网络的训练过程中，首先对编码器的第一层LSTM 参数进行随机初始化，利用自编码网络可以通过无监督的预训练过程学习到数据之间的关联特征的优点，进行参数调优. 自编码网络可以使得每层隐藏层的输入与隐藏层的输出最大概率的相同，从而减少输入的数据信息在网络层中传播而产生的信息损耗，自编码网络中每个网络隐藏层LSTM 的预训练过程如式（7）所示，预训练的目标是输出数据特征x′等于输入特征x. 在预训练过程中，选择L2 范数的平方来表示误差函数，用式（8）计算损失函数大小，并作为衡量无监督训练过程的信息损耗的指标. 计算如下：

其中，x是自编码网络的每个隐藏层LSTM 的输入（即输入数据单元某时刻的环境空气污染物浓度和气象数据）；X是隐藏层的输出；Wa∊Ru×v；ba∊Rv；σa是隐藏层的激活函数sigmoid（u×v表示的是权重矩阵维度）；x′是隐藏层的输出，Ws∊Ru×v，bs∊Rv，σs是隐藏层的激活函数sigmoid. 这样在训练过程中，X就可以看作是x的一种特征表示，同时x′表示为隐藏层的输出经过解码运算的结果，可最大程度逼近隐藏层的输入特征x. 在式（8）中，R（W，b）是权值衰减的正则化项，由式（8）可知，α为正则化系数，x′i和xi分别表示当前预训练层的输出和输入，n表示输入数据x的特征维度，loss（W，b）为损失函数.

编码层中的后续LSTM 层的输入即为上一层LSTM层的输出隐藏特征向量X，且都用（I）中相同的训练方式进行预训练.

（II）自编码网络的全局微调过程

全局参数优化过程中，本节将已预训练好的编码器参数迁移到当前的自编码网络中进行参数微调. 微调的过程可以解释为，将历史的污染物浓度和气象数据输入到编码器中进行时序特征提取，自编码网络将编码器的最终的隐藏状态作为解码器的输入并产生污染物浓度预测值. 全局微调的过程中，使用式（11）计算的均方根误差作为损失函数计算预测值与观测值之间的误差，通过随机梯度下降算法更新全局权重，直至模型收敛.

（3）CAE-Learning的全局训练过程

考虑到深层次的神经网络在训练时容易产生过拟合问题，本文在CNN 中加入了dropout 方法来避免过拟合，并且在整个模型中使用随机梯度下降法，通过误差反向传播的方式计算误差函数来对网络全部权重和偏置值的梯度进行更新，直至模型的性能符合期望，同时避免网络对训练数据的过度学习.

为解决深度网络在训练时易出现的过拟合问题，使用EN（Elastic Net）算法进行正则化约束，使目标函数在训练的fine-tuning 阶段达到最小，EN 的优势也在文献［36］中被实验证实，故选用式（10）作为目标函数：

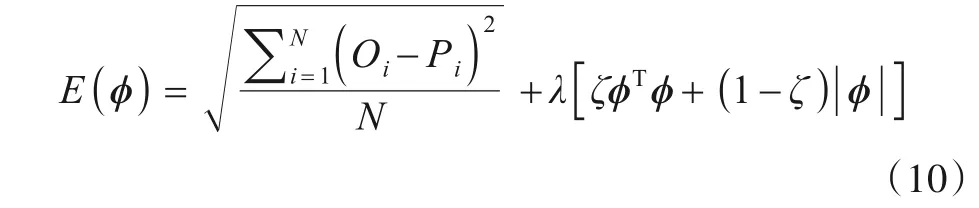
网络的目标函数设置为均方根误差和正则项之和. 式（10）等号右侧的前半部分为均方根误差，Oi是目标污染物的观测值（观察值），Pi是目标污染物的预测值，N为预测的时间段污染物浓度时间序列长度；后半部分中引入EN 算法进行正则化约束，λ为一个非负超参数，ϕ包含了整个训练过程参数，包括卷积层的权值矩阵、池化层的权值矩阵、自编码网络内部神经元之间传递信息的权值矩阵、全连接层的权值矩阵，ζ为控制L1，L2 惩罚大小使用的比例参数，ζ∊(0,1).

4 实验及结果

4.1 实验数据集和评价标准

本文将单城市多个站点的污染物浓度和气象数据作为实验对象，环境空气污染物PM2.5浓度为目标污染物. 本节实验目标城市为上海，其有9 个城市环境空气质量监测站点，分别为十五厂、虹口、上师大、杨浦四漂、青浦淀山湖、静安、浦东川沙、浦东新区和浦东张江，各个站点在地图上的位置如图5 所示. 图5 展示了上海市各个空气质量监测站点对特定目标站点（徐汇上海师范大学站）的多站点联合预测示意图.

图5 上海市多站点联合预测示意图

数据的时间跨度从2014年5月13日到2018年3月24日，其中包括环境空气污染物数据以及气象数据，监测时间间隔为一个小时. 其中训练数据有275 221 条，测试数据有17 830 条，数据特征包括：时间、PM2.5、AQI、PM10、SO2、NO2、O3、CO、气温、大气压、风向、风速、云量、气象条件、相对湿度和累积降雨量. 通过利用计算空值或异常值前后非空数据的平均值来填充数据集中的空值和异常值的方法来完成对实验数据集中空值和异常值的预处理工作，然后将数据归一化到［0，1］之间并整理成模型可接收的标准化数据格式.

在每个站点的16 个特征属性中，AQI、PM10、SO2、NO2、O3、CO 为相关污染物浓度特征数据，气温、大气压、风向、风速、云量、气象条件、相对湿度和累积降雨量为气象特征数据，PM2.5为目标污染物浓度，模型输入数据是过去72 h 内的上海市内所有9 个监测站点各个特征属性值的小时平均值，输出是特定一个站点（徐汇上海师范大学站）未来24 h 的PM2.5浓度的小时平均值序列. 在训练及测试时，模型每次获取训练数据集的时间长度为96 h，每次移动时间窗口为1，直到训练集或测试集中的数据读取完，完成一次数据集的训练或测试. 连续输入72 h 的数据包含上海市内所有监测站点的污染物浓度和气象数据的2 维矩阵，未来24 h 的污染物浓度观测值在训练阶段用于调整模型参数，在测试阶段用于评估模型的预测性能.

选择利用城市内多个站点而不是一个站点的数据来预测目标站点的目标污染物浓度可提升预测目标站点污染物PM2.5浓度的精确度［20］. 实验中，本文提出的预测模型和其他的对比模型均会在同一个测试集上进行10 次的预测实验，其预测结果的均方根误差的最终值为10 次实验误差的平均值，最大迭代次数为100 次. 关于数据集的其他详细说明可见表1.

表1 数据集详细参数

实验采用均方根误差（Root-Mean-Square Error，RMSE）、平均绝对误差（Mean Absolute Error，MAE）和相关系数（Corr）作为衡量预测精确度，RMSE、MAE和Corr的计算式如下：

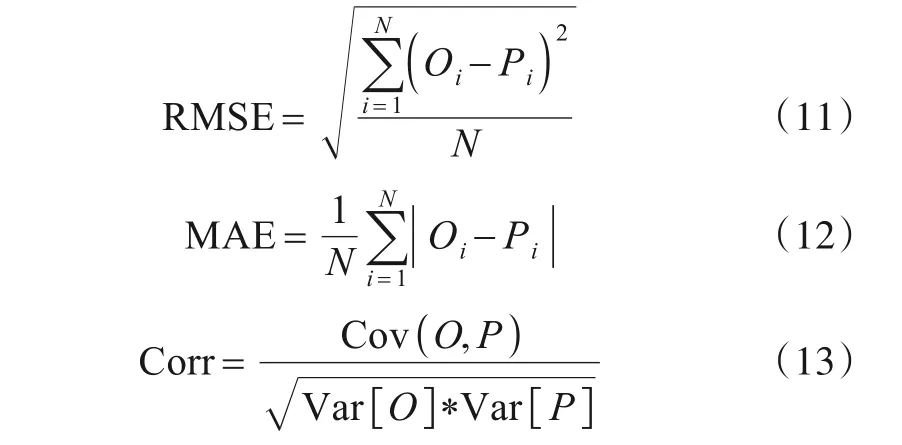
其中，Oi是目标污染物的观测值（观察值）；Pi是目标污染物的预测值；N表示测试集的大小；Cov（O，P）为观测值和预测值的协方差；Var［O］和Var［P］分别是观测值和预测值的方差.RMSE 和MAE 的值越小，Corr 的值越大，证明预测的准确度越高.

4.2 多站点联合预测效果对比

以下分析本文提出的CAE-Learning 融合神经网络和对比模型在测试数据集上不同迭代次数下的拟合趋势，以及为了对比CAE-Learning 性能，选用了3 种经典模型（BP 神经网络、RNN 和LSTM）作对比. 同时为了验证CNN和基于LSTM的自编码网络串行耦合的有效性，加入了CNN 单模型、CNN 与RNN 串行耦合的CNNRNN 模型、CNN 与LSTM 串行耦合的CNN-LSTM［37］模型，以及并行耦合的CNN+LSTM模型作为对比实验. 每个模型在测试的过程中使用的数据集和CAE-Learning所用相同，且都选择了相同迭代次数的拟合趋势进行比较，分别是10 代、30 代、50 代、70 代、90 代和100 代，每个模型的训练都是预测值向着真实值不断趋近的过程.

本文在主要考虑空间特征的时候，使用CNN 作为空间关联特征提取方法，得出的实验结果是RMSE 为27.068，仅使用LSTM 作时间序列预测，主要考虑时间关联特征时，实验结果是RMSE 为9.668，综合比较CNN、RNN、LSTM 以及CAE-Learning 模型，当综合时空特征的时候，实验效果要比仅考虑空间特征或时间特征的模型效果要好.

图6 即为CAE-Learning 模型在根据过去72 h 的多站点污染物数据及气象数据对未来24 h 内的PM2.5的浓度作出的预测情况的拟合曲线. 从图6 可以看出，CAE-Learning 模型可以达到很好的拟合效果，只在第10 代的时候误差较大，但是接下来的拟合情况都有明显提升，在整体预测趋势以及精确度方面都达到了很好的预测效果，能够使预测值无限接近于真实值，RMSE 平均值低至8.880（下文会有表格详细描述）.

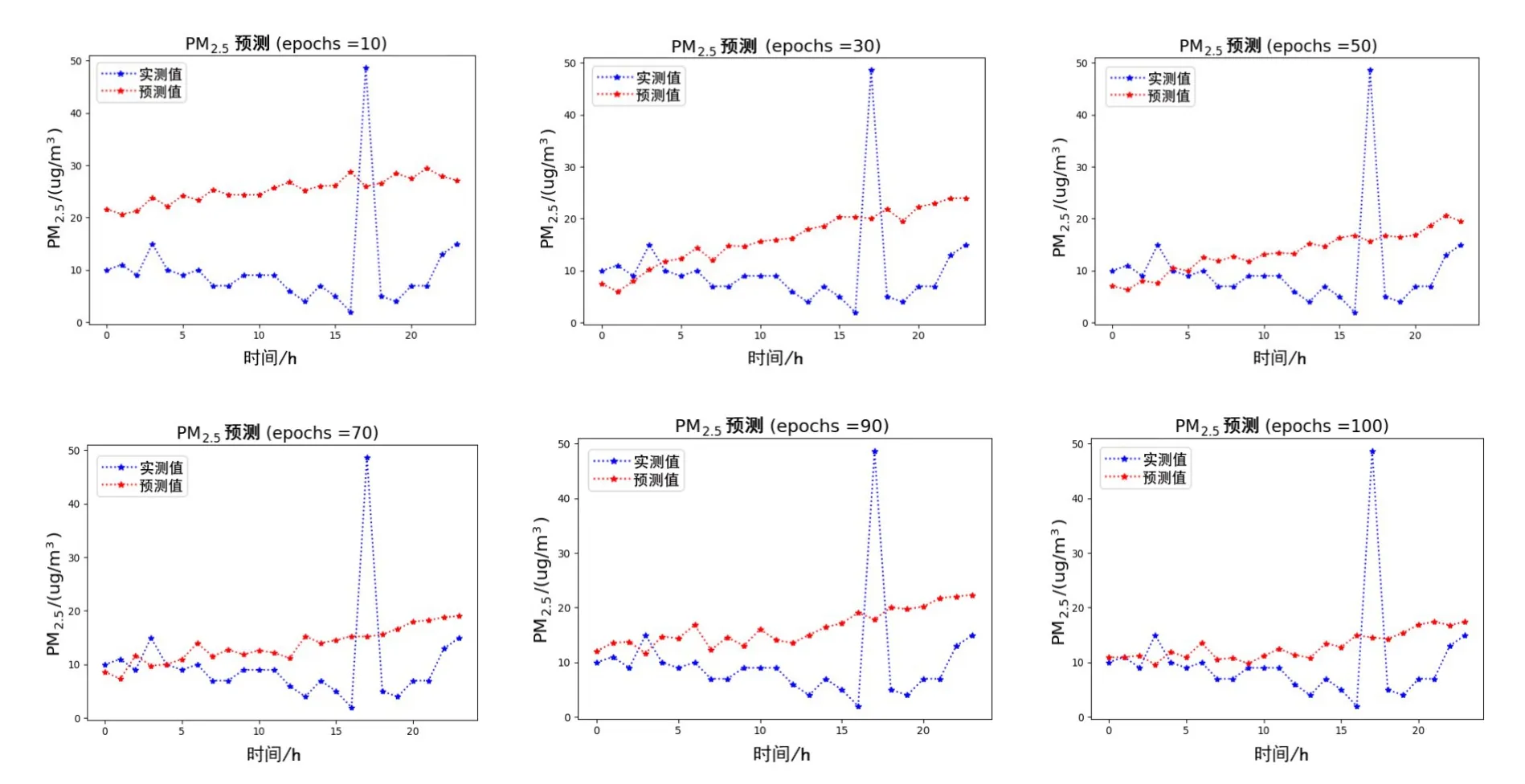
图6 CAE-Learning的多站点联合预测结果

图7 为CNN-LSTM 模型的拟合结果图，从图中可以看出，该模型在50 次迭代之前精确度比较低，50 代之后才慢慢有较好的拟合趋势. 作为CAE-Learning 的对比实验，在提取空间信息时采用相同的CNN 结构的情况下，由于基于多层LSTM 组成的自编码网络能够根据编码器中提取到的上一时刻的信息，输入到解码器中作下一时刻的预测，其对时间序列的提取效果较单独的LSTM 模型会有较大的提升. 从图6、图7 的实验结果对比中也可以发现，自编码网络在整体的预测趋势及精确度上要优于LSTM，且预测稳定性较高.从而可以比较得出，基于LSTM 的自编码网络比传统的LSTM 模型在较长时间内的时序预测方面性能更好.

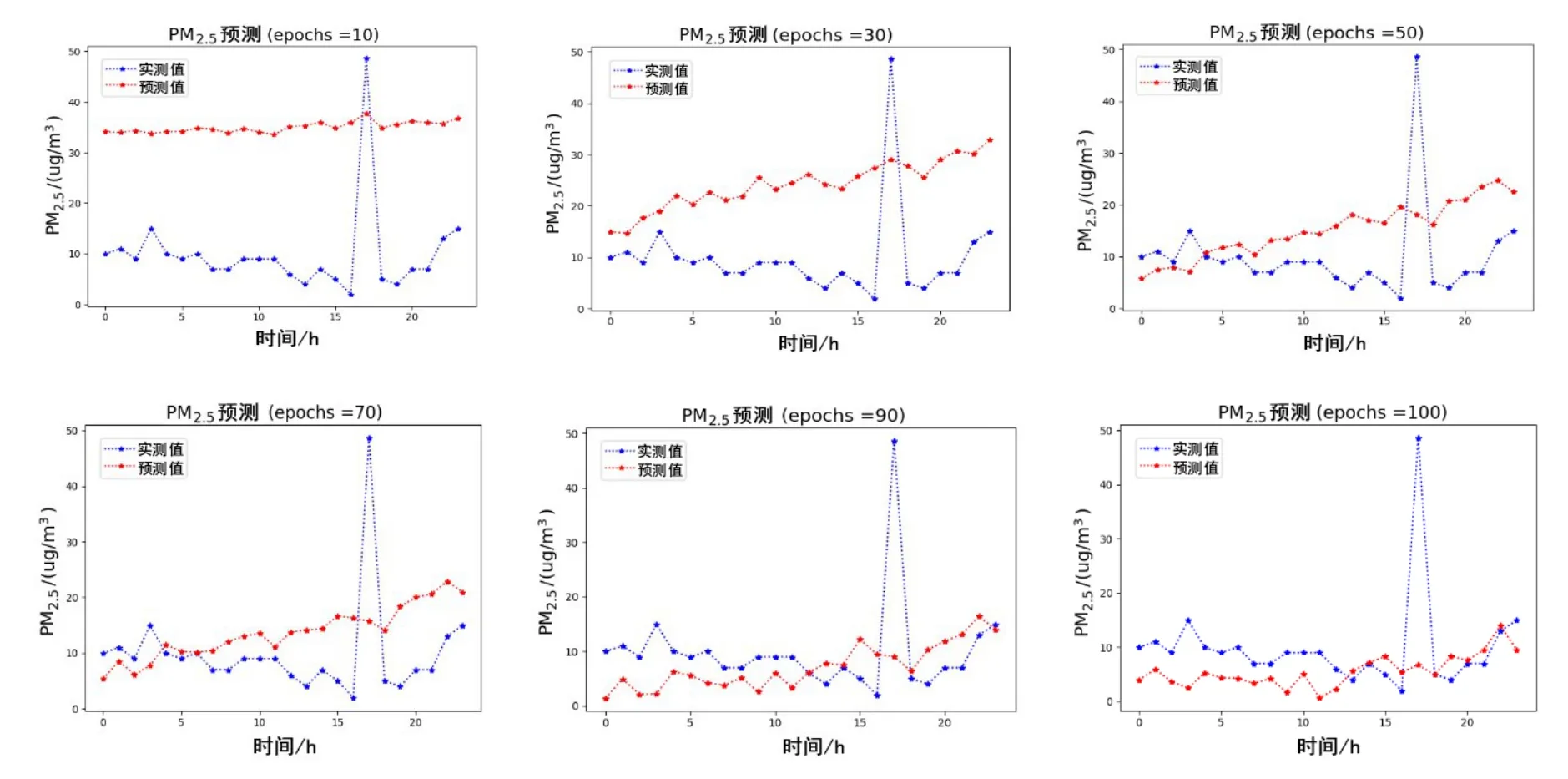
图7 CNN-LSTM的多站点联合预测结果

对比模型CNN-RNN 在相同的训练数据集下，与CAE-Learning 模型以及CNN-LSTM 模型比较而言，拟合的效果稍显逊色. 从表2 的评价指标来看，CNNRNN 的RMSE 值为15.710，CNN-LSTM 的RMSE 值为9.173，CAE-Learning 的RMSE 值为8.880，从中可以得出，在空间信息提取器均为CNN 的情况下，采用端到端模型作为后续的时序提取模型会取得更好的预测效果.

相较于CNN-LSTM 以及CNN-RNN 等串行耦合的预测模型而言，CNN+LSTM 模型采用了并行的模型融合方式对时空数据进行耦合，如图8 所示. 即在训练过程中，同时对CNN 以及LSTM 进行训练，以并行的耦合方式同时获取多站点数据之间的时间、空间特性，对CNN 以及LSTM 得到的预测结果进行综合，得到两个模型的并行的耦合结果的融合. 由于并行的CNN+LSTM 模型在时空信息提取的过程当中，CNN 与LSTM两个模型会同时提取到数据集中的时间及空间信息，最终进行融合的时候，会一定程度上造成信息的冗余. 结合实验结果来看，CNN+LSTM 模型的预测值与真实值之间的拟合程度随着模型迭代次数的增加反而呈现降低的趋势，最终的RMSE 值为22.902，与CAE-Learning 以及CNN-LSTM、CNN-RNN 等串行的时空信息提取模型相比较而言，预测的结果也相对较差.

CNN 单模型、LSTM 单模型、RNN 单模型以及BP 神经网络模型的实验效果均与CAE-Learning 的预测结果存在一定的差距. 其中，CNN单模型能够更好地获取空间信息，体现在实验数据上的是CNN 取得的相关性系数比较高；而LSTM 单模型能够较好地获取时序信息，迭代次数越多，可以得到更好的预测效果，但是由于其自身无法捕获长时间数据依赖，最终预测效果不如本文提出CAE-Learning 模型；BP 神经网络的最终预测效果在3个网络中最差.

为了更直观地展示本文提出的CAE-Learning 模型的优势，每个模型训练1 次收敛的时间（用训练时间表示）以及在测试集上最终的RMSE、MAE 和相关系数Corr（计算方法参考式（11）、式（12）和式（13））在表2 中列出.

Corr 的值表示预测值和观测值之间的关联度，Corr的值越高，表示两者关联度越高，模型的性能越好. 当Corr 的值达到1 时，表示预测值和观测值完全相关. 实验结果分析如下.

（1）将LSTM 与其他单模型进行对比，由于LSTM 在处理时间序列预测任务时，比RNN、CNN、BP 网络具有更好的适用性，所以LSTM 在实验结果上也要比其他模型好，从表2 中也可以获得与模型机理一样的实验结果：LSTM 的RMSE 的值最小可达9.688，Corr 的值最大可达到0.958，优于其他的单模型.

（2）将CNN 和其他的单模型进行对比，CNN 具有提取污染物与气象数据的相关性的能力，虽然其在时序预测效果上与其他单模型有一定差距，但是其在预测污染物变化的趋势上具有一定的优势. 从图8以及表2中也可以发现这一特点，CNN 的相关系数最大可以达到0.980，这表明在考虑了污染物和气象数据的空间相关性后，可以更准确模拟出污染物浓度的变化趋势. 而CNN 的RMSE 及MAE 值均比其他单模型高，即比其他单模型在时序预测上效果要差.

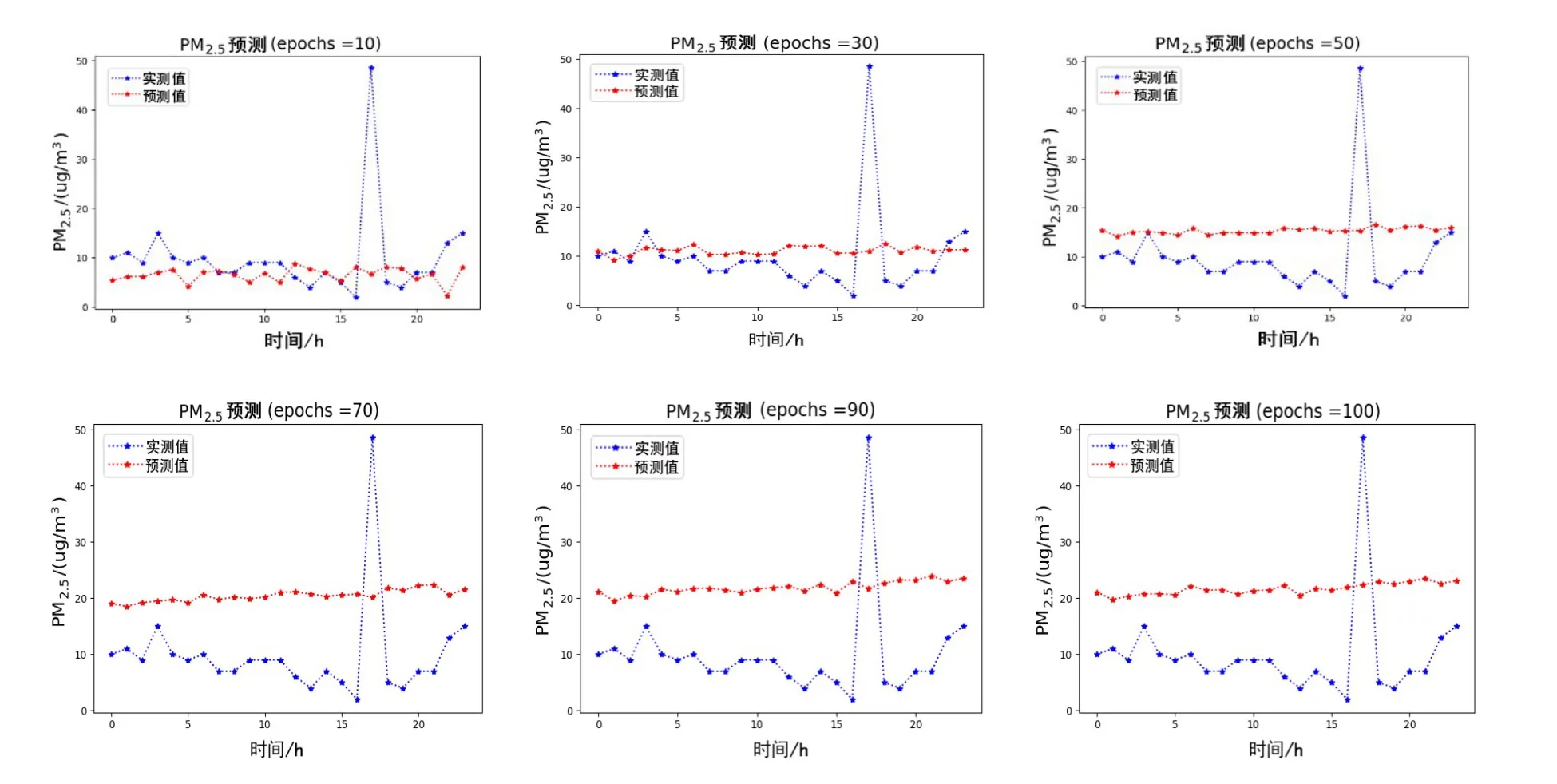
图8 CNN+LSTM并行的多站点联合预测结果

表2 每个模型的RMSE、MAE、相关系数和训练时间

（3）CAE-Learning 与CNN-LSTM、CNN-RNN 以及并行的CNN+LSTM 模型进行比较，由于CNN-LSTM 可以由CNN 提取污染物数据及气象数据间的空间关联性，再由LSTM 来提取时序关系，因此可以达到比其他单模型以及组合模型都要好的预测效果. 从表2及图6、图7可以看出，CNN-LSTM 的预测效果仅次于CAE-Learn⁃ing，其RMSE 最低可以达到9.173.CAE-Learning由于其结合了基于多层LSTM 的自编码网络和多维卷积CNN的优势进行污染物浓度预测任务，能够充分挖掘数据间的时空相关性，从表2及图6可以看出，与其他模型相比较，该模型在PM2.5预测方面具有最好的预测效果及性能，RMSE 的值最小可以达到8.880，Corr 值最高可达到0.980.

4.3 CAE-Learning的泛化性

为了验证模型的可迁移性以及泛化性能，选取杭州、苏州、重庆、北京作为验证CAE-Learning 模型泛化性能的城市，做城市内多站点污染物浓度的联合预测，并与在上一节中预测效果仅次于CAE-Learning的CNNLSTM 进行比较，证明CAE-Learning 的泛化效果. 选取的城市的每个监测站点的数据特征和时间跨度与上海市监测站完全相同.

（1）杭州市实验结果

实验将杭州和睦小学作为目标站点，预测该站点的PM2.5浓度变化，其余的滨江、西溪、千岛湖、下沙、卧龙桥、浙江农大、朝晖五区、临平镇、城厢镇、云栖，这10 个站点作为相关站点，做时空预测. 实验结果如图9、图10及表3所示.

表3 模型在杭州市数据集下的RMSE、MAE、相关系数和训练时间

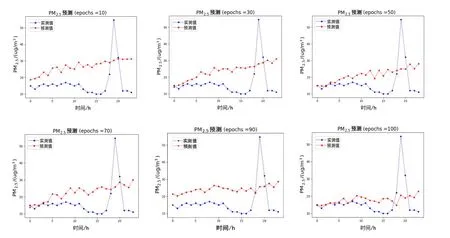
图9 CAE-Learning的多站点联合预测结果

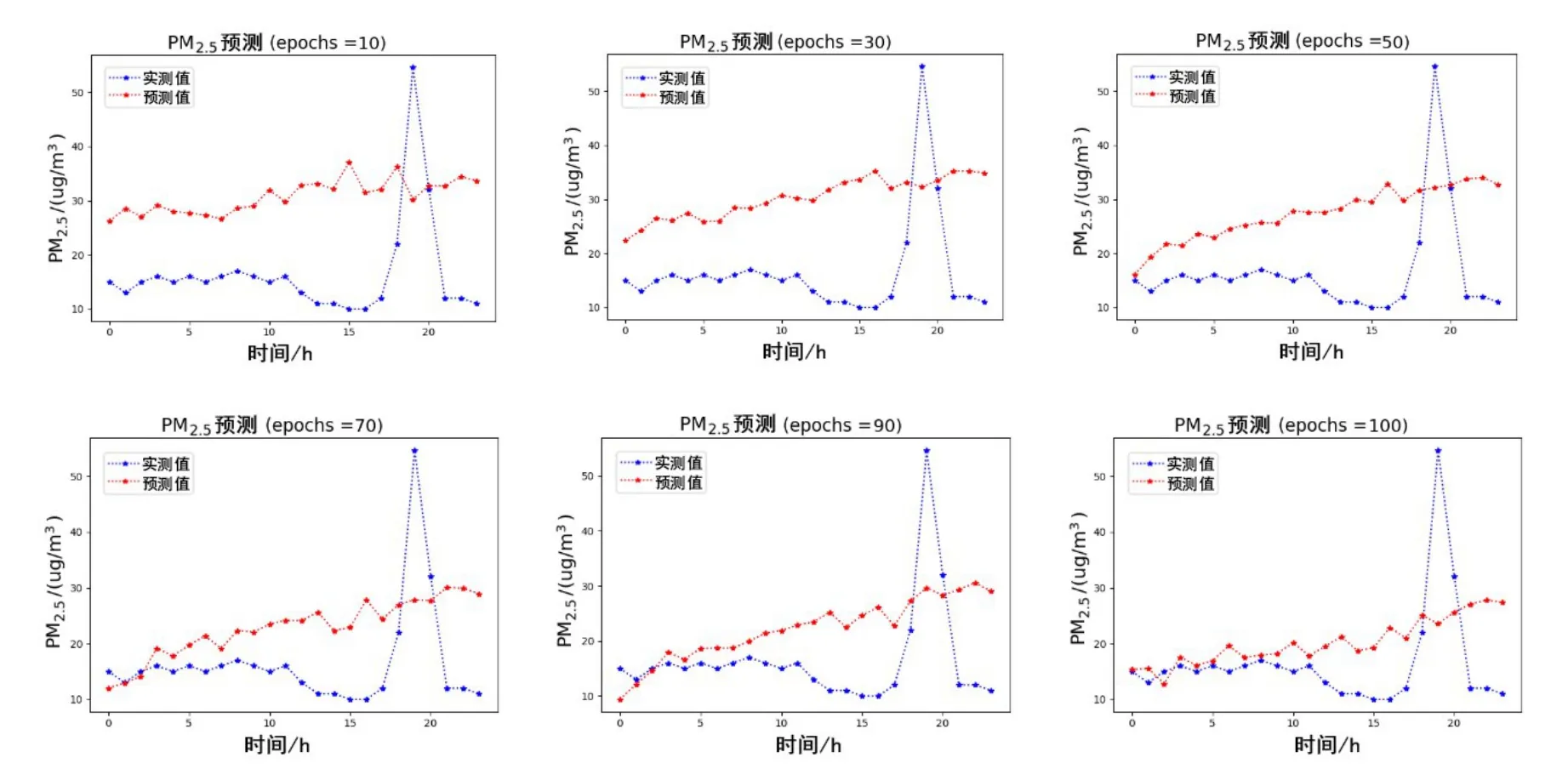
图10 CNN-LSTM的多站点联合预测结果

（2）苏州市实验结果

实验将苏州相城区作为目标站点，预测该站点的PM2.5浓度变化，其余的上方山、南门、彩香、轧钢厂、吴中区、苏州新区、苏州工业园区，这7 个站点作为相关站点，做时空预测. 实验结果如图11、图12 和表4所示.

表4 模型在苏州市数据集下的RMSE、MAE、相关系数和训练时间

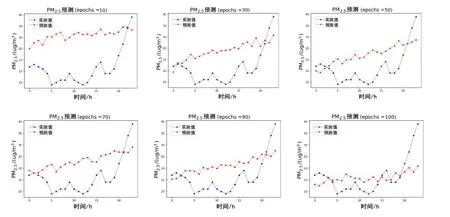
图11 CAE-Learning的多站点联合预测结果

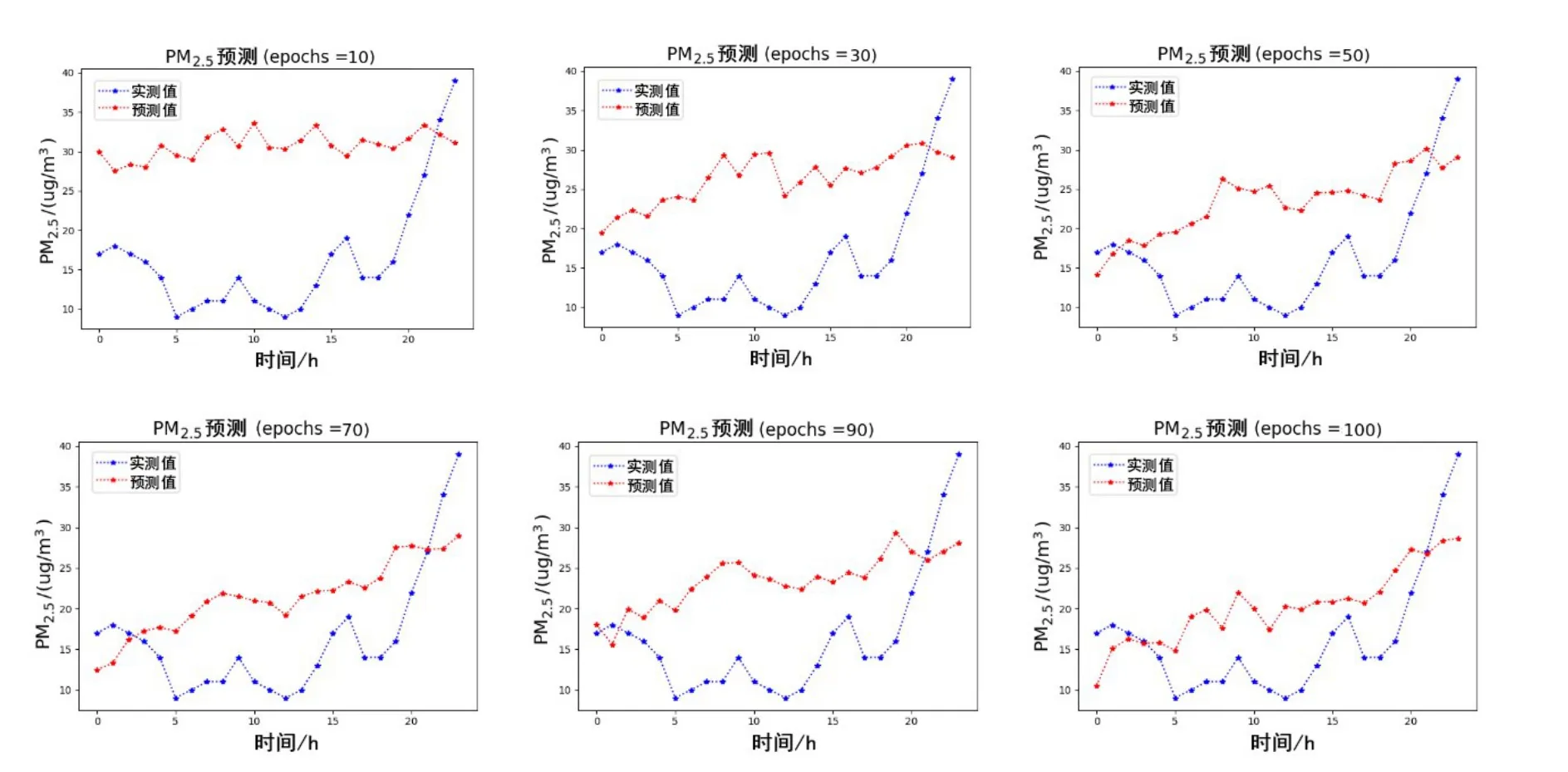
图12 CNN-LSTM的多站点联合预测结果

（3）重庆市实验结果

实验将南坪作为目标站点，预测该站点的PM2.5浓度变化，其余的缙云山、高家花园、天生、两路、虎溪、唐家沱、茶园、白市驿、解放碑、杨家坪、空港、新山村、礼嘉、蔡家、鱼新街、南泉，这16 个站点作为相关站点，做时空预测. 实验结果如图13、图14和表5所示.

表5 模型在重庆市数据集下的RMSE、MAE、相关系数和训练时间

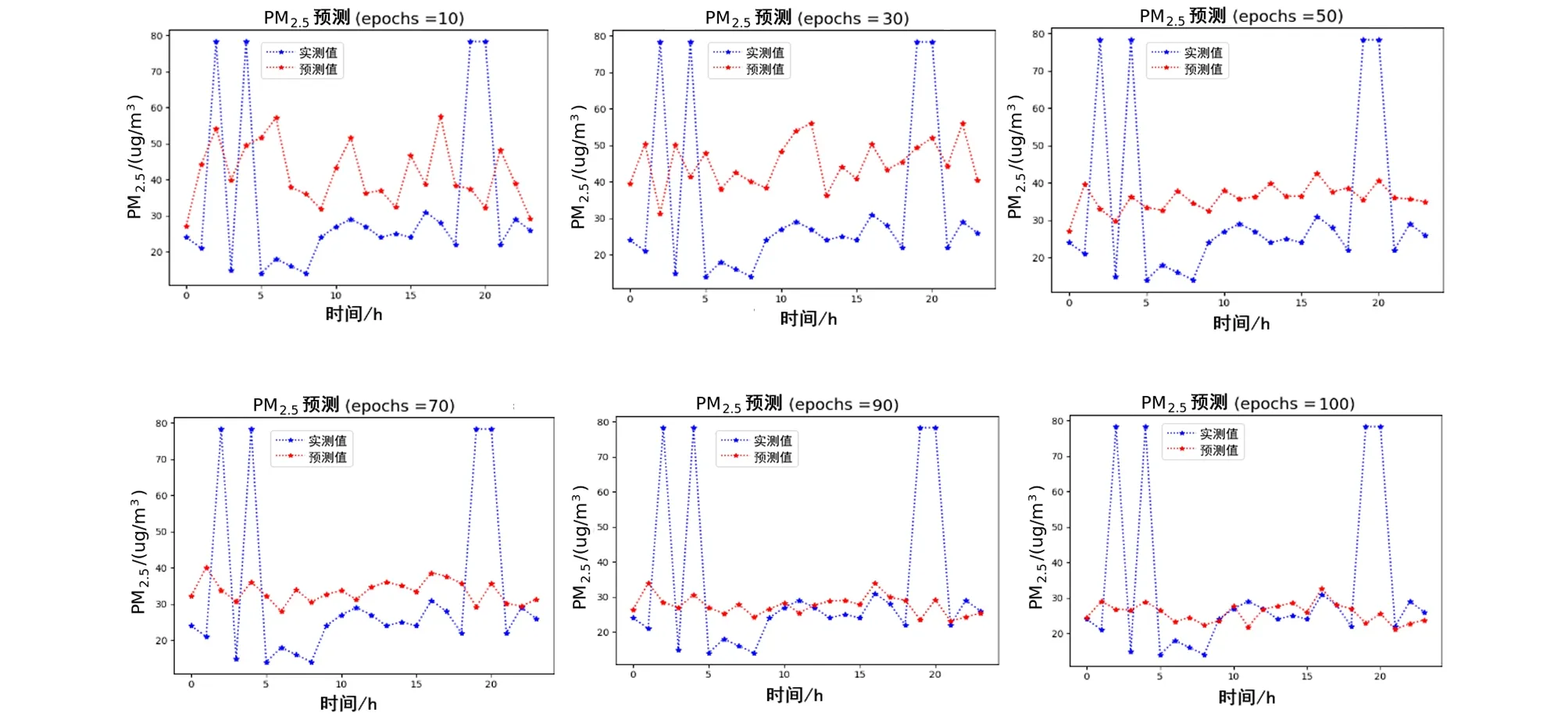
图13 CAE-Learning的多站点联合预测结果

图14 CNN-LSTM的多站点联合预测结果

（4）北京市实验结果

实验将顺义新城作为目标站点，预测该站点的PM2.5浓度变化，其余的万寿西宫、定陵、东四、天坛、农展馆、官园、海淀区万柳、怀柔镇、昌平镇、奥体中心、古城，这11 个站点作为相关站点，做时空预测. 实验结果如图15、图16和表6所示.

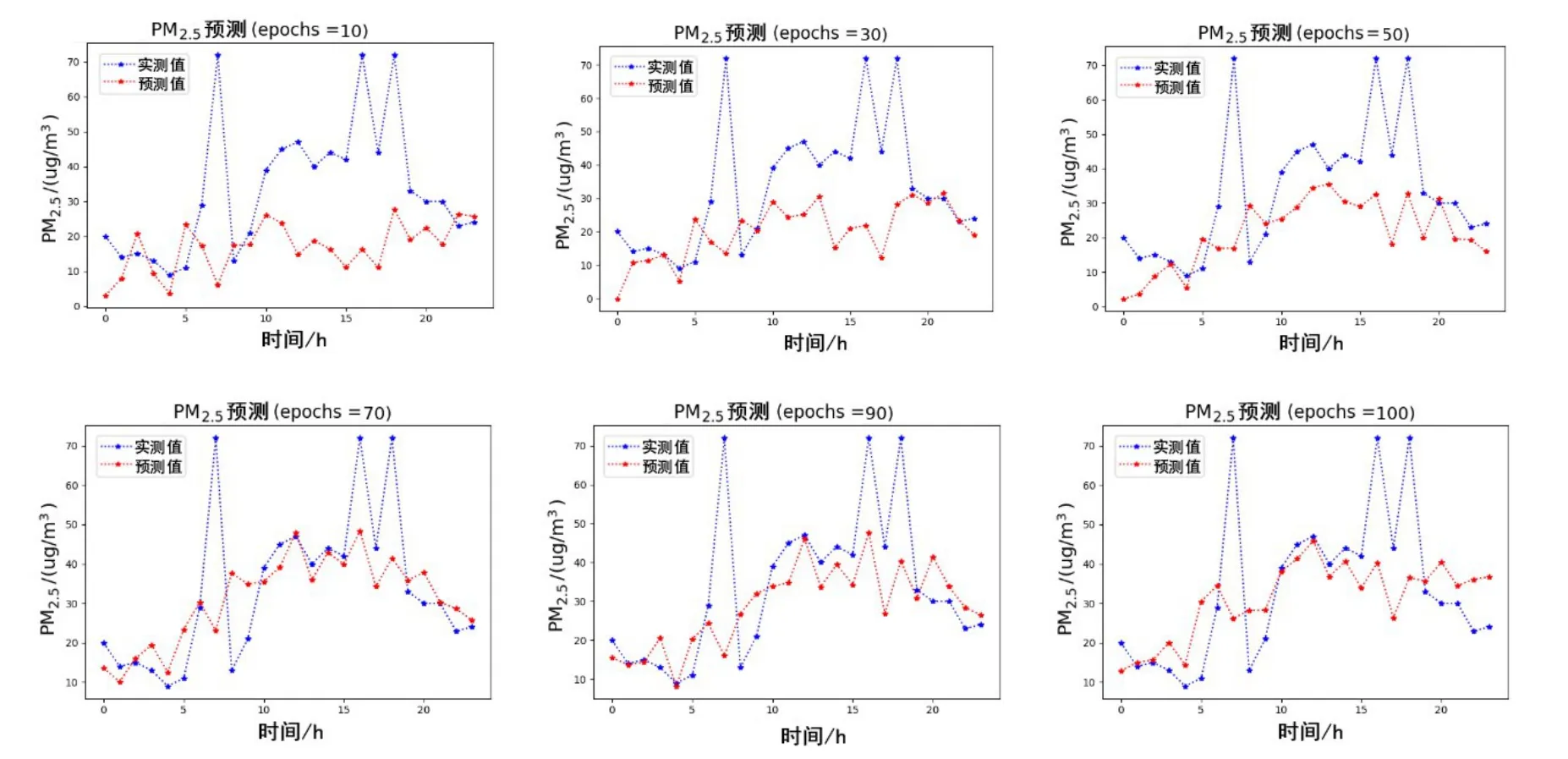
图15 CAE-Learning的多站点联合预测结果

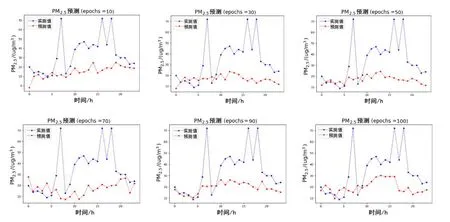
图16 CNN-LSTM的多站点联合预测结果

表6 模型在北京市数据集下的RMSE、MAE、相关系数和训练时间

通过CAE-Learning 及CNN-LSTM 两个模型在杭州、苏州、重庆、北京这4个城市的空气污染浓度预测实验上的对比可以发现，本文提出的CAE-Learning 模型迁移到其他城市做多站点联合预测时，还是可以充分发挥其模型的内在优势的，能深度提取多站点间的时空关系，对长时间序列预测问题能够做到有效的预测.在迭代到100代的时候，不同城市多站点间的实验结果都表明：CAE-Learning 比CNN-LSTM 对真实值的拟合程度更高，预测效果更好. 从表3、表6中列出的评价指标RMSE、MAE 和相关系数Corr 的比较中也验证了CAELearning的预测效果更好.

5 总结

本文利用城市内多站点的监测数据，提出了基于CNN 和自编码网络的时空融合模型（CAE-Learning）来联合预测目标站点目标污染物浓度的方法.CNN 是模型的底部，用于提取空间特征，卷积和池化后获得数据之间的相关性. 基于LSTM 的自编码网络是模型的顶部，用于提取输入的时间序列特征.

CAE-Learning 模型对应的预测任务是用单城市多个监测站点的污染物浓度数据和气象数据作为模型的初始特征输入，来预测特定目标站点未来N小时内的污染物浓度. 从基于真实数据的实验证明，对于时空融合的时间序列预测问题，CAE-Learning和其他对比模型相比有很好的预测性能，在上海市的测试数据集上获得了不错的预测效果后，在杭州、苏州、重庆、北京这4个城市也有着很好的表现，具有较好的泛化能力. 与传统模型相比，CAE-Learning不仅考虑了空间关联性——城市内多站点之间污染物浓度的相互影响，而且考虑了污染物浓度的时间关联性——污染物浓度前后时间段内的相互影响，从而使实验的预测效果有了明显的提升.

该模型相对于传统机器学习方法和单一经典网络有较好的性能提升，已经多次在国家级区域空气污染监测预报任务中作为实际辅助模型之一得到应用，体现出较好的应用效果和价值. 但由于数据方面的限制，该模型在不同地形、不同气候带、不同城市群特征、多模态数据等细化环境下的性能状态仍有待检验. 因此，未来的研究工作将集中在多种类、多模态气象及污染物数据间的维度分析、语义提取、关联性分析及多个预测模型的融合方面，进一步提升最终预测的精确度.