融合深度特征的电磁频谱异常检测算法
彭 闯,王伦文,胡炜林
(国防科技大学电子对抗学院,安徽合肥 230037)
1 引言
随着电磁设备以及通信技术的发展,电磁频谱资源变得愈加宝贵. 在民用领域,移动通信、物联网、移动互联网、广播电视、铁路乃至于气象播报都依赖频谱实现[1]. 在信息化军队的建设背景下,未来信息化作战将有大量的先进军事装备编入现役,各装备都装载有多个用频设备,对频谱资源的管理提出了新的要求. 认知无线电技术被认为是提高频谱利用率和缓解频谱稀缺的一种有效方法[2],但大规模的频谱管理易受到攻击及干扰,因此对频谱异常检测的研究是当前认知无线电领域的热点.
频谱异常检测是认知无线电以及频谱监测领域的重要组成部分,能够实现对恶意干扰、用户冲突以及非法占用等异常状态的检测,对保障航空运输安全、提升通信质量有重要作用. 同时,电磁频谱异常检测及研究对无线电设备管理以及电磁环境态势评估具有重要意义. 为实现电磁频谱异常检测,学者们已经取得一定成果. 传统的电磁频谱异常检测算法多是利用信号统计特征进行数据分析实现的. 文献[3]提出了基于二维交叉的异常检测方法. 文献[4]改进了奇异谱分析方法,构建了一个滑动窗口在线异常检测器. 文献[5]通过对时间序列分析实现对无线电频谱异常的检测,该方法无需历史数据支持,即可识别典型频谱异常类型. 此外,文献[6]结合信息熵改进聚类算法实现异常检测.上述基于信号分析的异常检测算法虽然效果不错,但都存在无法处理高维数据、对首次出现的异常信号不够灵敏等问题. 随着人工智能行业的不断发展,深度学习展示出了强大的数据分析能力,学者们使用深度学习在异常检测领域也已经取得了一定成果. 文献[7,8]使用监督学习的方法实现了频谱异常检测,但该类方法仅能识别确定类别的异常. 在实际的频谱数据中,异常数据获取困难,难以支撑标签化的深度训练. 因此,利用无监督学习的方法,基于频谱预测的异常检测技术是当前研究的主要方向. 文献[9]提出一种基于对抗自编码器(Adversarial AutoEncoder,AAE)的频谱预测算法,并基于该预测方法实现了一种异常检测系统SAIFE. 文献[10]使用LSTM 网络对LTE 信号频谱中的多种异常状态进行检测,并基于迁移学习研究了网络模型的跨频段使用问题. 文献[11]针对卫星通信存在的异常频谱状态,使用LSTM 实现了多变量异常状态以及细微异常状态的检测. 文献[12]使用卷积神经网络提取深度特征,实现了异常检测. 文献[13,14]将En⁃coder 与GAN 网络相结合,提出了一种新的异常检测思路,但该算法相比于常规模型增加了Encoder 以及鉴别器两个模块,网络复杂度较高. 文献[15]研究了多传感器场景下无线通信频谱异常检测问题,通过深度学习将数据转移到高维特征空间,解决了特定场景下的异常检测问题. 可以看出,现有算法多是基于循环神经网络实现,这是因为该网络具有强大的序列处理能力,能够提取频谱数据间的关联性实现频谱数据的预测和生成. 但是频谱数据包含频点较多、时序较长,而循环神经网络需要一维序列作为输入,弱化了数据之间的联系.
针对上述基于深度学习的频谱异常检测算法存在的频谱数据预测精度不高等问题,本文提出一种融合深度特征的电磁频谱异常检测方法. 首先构建深度特征提取网络,该网络包含一个能够分级提取深度特征的两路多层的CNN 以及一个LSTM;其次通过池化、合并等操作提取各级深度特征并进行融合,实现高精度的频谱数据预测;最后,计算预测数据与真实数据的均方误差,判别频谱异常. 本算法能够在无监督学习的条件下实现多种类异常状态检测. 实验中,通过仿真的方式对公开频谱数据增加异常干扰,在多个频段对算法性能进行验证. 结果表明,相比于现有算法,本算法能够显著提高电磁频谱数据预测精度,有效地实现电磁频谱数据异常状态检测.
2 频谱异常检测算法框架
假设数据集XS可以认为是一个超集,其包含来自不同频段的多种信号,XS=XS0∪XS1∪…∪XSn来源于时间序列信号,x∊XS为来源于任意无线频段基于频率的功率谱密度(Power Spectral Density,PSD)向量. 此外,假设该源数据集XS包含的大部分无线电信号都是正常行为,异常行为出现的概率极低.
基于频谱预测的异常检测的目标是寻找一种能够学习源数据分布p(XS)的模型,并且该模型能够检测目标向量是否偏离数据分布. 对于每一个属于测试数据集的向量x∊XS,网络模型应该能够判断向量是正常行为H0还是异常Ha. 其中,H0为来源于p(XS)的数据,Ha为不属于p(XS)的数据[9]. 基于频谱预测的异常检测算法整体框架如图1所示. 其中,m为历史数据时间步长,k为预测数据时间步长,n代表频点数,s为历史频谱数据组数,红色模块代表已完成训练的预测模型,绿色模块代表鉴别器,在本文中选用MSE 函数实现频谱异常数据的鉴别,如式(1)所示,̂为预测频谱数据矩阵,P为实际接收频谱数据矩阵.

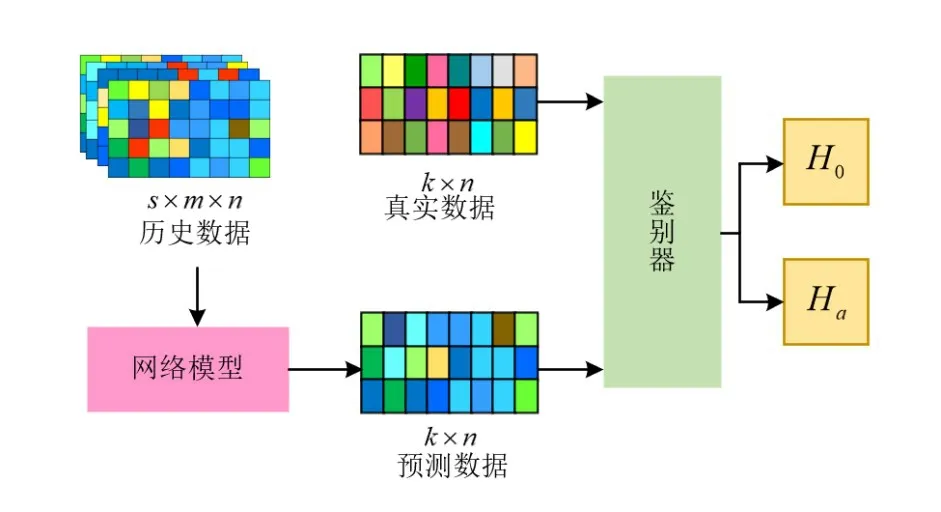
图1 基于频谱预测的异常检测算法框架
本文基于频谱预测的异常检测是基于以下2 个条件实现的:(1)源数据集中出现异常的概率非常低,不影响网络模型的训练;(2)训练数据以及测试数据没有进行异常标记,数据仅能支持模型进行无监督学习.
3 基于深度特征融合的异常检测模型
目前的基于深度学习的异常检测算法多是使用循环神经网络实现,该网络具有强大的序列处理能力. 但是频谱数据包含频点较多、时序较长,循环神经网络需要将频谱数据转化为列向量,弱化了同频点之间数据的联系. 为解决该问题,本文参考Unet[16]以及CNN+LSTM[17]模型构建了一种深度特征提取网络. 该网络使用多级双层CNN 以及LSTM,分层提取深度特征,接着,通过池化、卷积以及合并等操作将提取的多层深度特征进行融合,实现高精度的频谱数据预测,最后通过鉴别器,实现频谱数据的异常检测.
3.1 数据预处理
电磁频谱的研究很难精确到具体数值,因此常见的频谱测量数据是连续的功率谱密度值,其主要机理是根据功率谱密度的大小判断该频段的状态. 为方便进一步处理、分析,在本文对频谱数据的预处理中,以原始数据的最大值为上界、最小值为下界,将频谱数据进行归一化处理. 数据的归一化处理能够提升模型精度以及收敛速度,并能够防止模型出现梯度爆炸问题.
本文研究的异常检测问题是基于高精度的频谱预测实现的,由于一个频段内包含多个信号,在频谱数据上呈现出强弱不同的多个频带. 这些频带内数据较为稳定,其可预测性强、预测难度小;频带边缘以及频带交接频点的数值变化较快,其可预测性弱、预测难度较大. 现有算法已经能够很好地实现强频带数值的计算,但仅使用原有历史频谱数据很难提升算法在变化数值预测方面的性能. 现有算法多是基于LSTM 及其改进网络实现的,而该类网络很难实现多维数据的并联输入,限制了数据预处理方式的进步. 因此,本文主要使用卷积层构建网络,该类网络能够允许多维并联数据的输入并能够通过卷积操作不断提取深度特征,实现对变化数据的高效预测,增强异常检测算法性能.
为提取频谱数据的变化特征,分别从频域、时域两个领域去除均值并取绝对值,得到频域数值变化特征以及时域变化特征. 假设每个样本为m个时刻n个频点的频谱数据Dmn,则其频域数值变化特征RFij以及时域数值变化特征RTij如式(2)~(5)所示:

其中,MTi为时域均值;MFj为频域均值. 实验中发现直接取数据与均值的差值会导致预测结果中出现负值,而对差值取绝对值能够避免这种情况的出现,取得更高的预测精度.
3.2 基础网络模块
为提升网络的深度特征提取能力,本文决定同时使用CNN 以及LSTM 两种基础网络模型. CNN 是一类包含卷积计算且具有深度结构的前馈神经网络,具有强大的表征学习能力. 通过卷积操作,CNN能够实现数据维度的变化,提取的输入信号的高维特征,相比于原始信号更能捕捉数据变化的潜在规律. 卷积核的尺寸决定了网络提取特征的维度,卷积核的堆叠可以获得更为丰富的深度数据.
基础卷积操作[18]如式(6)所示,激活函数使用线性整流(Rectified Linear Unit,ReLU)函数,如式(7)所示:

式(6)中,f表示激活函数;I表示输入矩阵;K为卷积核矩阵. 式(7)中,x表示输入. 当x>0 时,ReLU 函数输出与输入为线性关系;当x≤0时,ReLU函数输出为0.
LSTM 网络是一种特殊的循环神经网络,能够有效地解决网络训练过程中的梯度爆炸问题,尤其对于长序列处理问题,相比于基础的RNN有明显的性能优势.LSTM 内包含输入门、遗忘门以及输出门3个控制单元,通过门控状态来控制传输状态,记住需要长时间记忆的信息,忘记不重要的信息[19]. 单个LSTM模块如图2所示,其中红色是遗忘门,绿色是输入门,蓝色是输出门.

图2 单个LSTM模块示意图
遗忘门中的遗忘因子ft决定了上一时刻的单元状态Ct-1有多少信息保留到当前时刻的单元状态Ct;输入门决定了当前时刻网络的输入xt有多少保存到单元状态Ct;输出门决定了Ct有多少信息输出到LSTM 的当前输出值ht,如式(8)所示:
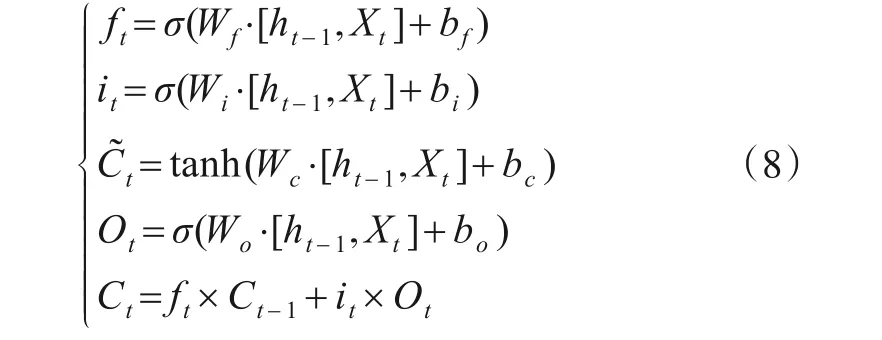
其中,Wf,Wi,Wc,Wo均为权重;bf,bi,bc,bo为偏置项;σ,tanh 为网络的激活函数;͂ 为暂时单元状态;Xt为当前的输入;Ct-1为上一单元的单元状态;ht-1为上一单元的输出.LSTM 能够高效学习数据的内在规律,实现频谱的预测.
在网络的训练过程中,选择MSE 作为损失函数,与图1网络框架中的鉴别器保持一致. 为优化CNN 性能,使用Adam 优化器代替随机梯度下降(Stochastic Gradi⁃ent Descent,SGD)算法来最小化损失函数. 相比于SGD算法,Adam 优化算法能够通过计算梯度的一阶矩估计和二阶矩估计为不同的参数设计自适应性学习率. 当网络训练结束后,能够拟合出训练数据中的模型各层权值和偏置,然后利用模型参数实现测试频谱数据的预测及生成.CNN 以及LSTM 均具有强大的数据处理能力,能够以不同的方式提取数据的特征. 因此,本文将两种模块组合使用构建深度学习网络,实验证明这种网络比仅使用CNN或LSTM拥有更好的异常检测性能.
3.3 网络模型
本文同时使用CNN 以及LSTM 两种基础模型构成深度网络,网络模型整体结构如图3 所示.CNN 特征提取网络能够有效提取频谱数据的高维深度特征. 该网络主要使用了卷积层、池化层(pooling layer)以及连接层(concatenate layer)作为基础模块,网络共3 层,分为输入层、并联推断层、融合推断层.LSTM 特征提取网络由LSTM 层以及全连接层(dense)构成,由于LSTM 对数据输入的要求与CNN 网络不同,需要对数据形状进行改变(reshape),才能实现网络的正常运行以及深度特征的融合.

图3 网络模型整体结构图
图3 中输入数据为包含频点数为n,已知时间长度为m,预测时长为k. 网络的输入为实际频谱数据,每个样本为m×n矩阵.CNN 特征提取网络输入为经过预处理后m×n×3 的三维矩阵. 其中,预处理首先提取量化后数据的时域、频域变化特征;接着,将变化特征与量化频域数据并联,并将数据归一化.
并联推断层是CNN 特征提取网络的核心,其结构如图3 中黑色虚线框内所示. 该层输入为输入层输出的m×n×3 的三维矩阵,输出为k×n的矩阵,其中k为预测时长. 并联推断层的功能是学习输入数据的多维度特征,并实现频谱数据的预测及生成. 该层内含2 路3 层卷积模块,相比于仅使用单路的卷积模块,2 路3 层卷积模块能够提取各频点数据间多种深度特征. 卷积层在卷积过程中对输入边界填充0,以控制卷积后特征矩阵的大小,即卷积操作后输出数据的矩阵时域、频域维度不变,实现下一步的融合推断. 上下支路均使用卷积操作将输入数据通道(channel)数提升至32 维,提取数据高维特征并增强网络的拟合能力. 上支路与下支路分别提取特征,数据经卷积操作后维度为m×n×32,为融合上下两路的不同特征,还需通过池化层以及连接层,实现数据的维度变化以及合并. 最后,再次通过卷积操作推断数据内容,并实现通道数的降低,改变数据维度为k×n. 上下两路特征经过池化层、连接层以及卷积层实现该层的特征提取. 在完成本层特征提取后,上下两支路再次卷积获取更深层特征. 随着并联推断层的递进,网络能够不断提取深度特征,提升模型性能.
融合预测层结构如图3中红色虚线框内所示,其输入为并联推断层各级以及LSTM 层输出的深度特征,输出为频谱预测结果,作用是融合各级深度特征并生成预测数据. 并联推断层各级输出结果为k×n,使用连接层对各级输出进行并联,则数据维度为k×n×4. 添加一个卷积核尺寸为1×1 的卷积层,降低数据规模并对融合结果进行再次选择. 经卷积操作后,输出即为矩阵维度为k×n的预测频谱数据.
通过对网络结构的分析可知,网络使用CNN 以及LSTM 分别提取深度特征. 并联推断层中含有两路多层的卷积模块,能够多次提取不同的深度特征. 由于结构上的差异,LSTM 模块生成的特征不同于并联推断层提取的特征. 本文将并联推断层提取的不同层级的特征与LSTM 提取的特征融合,提升算法的性能. 总的来说,基于本文模型的异常检测算法可以归纳为以下3个步骤:首先,使用两路卷积模块分别提取不同的深度特征并进行组合;接着,将多层CNN 提取的特征与LSTM网络提取的特征并联;最后,通过卷积操作选择特征并降维,实现频谱数据的预测. 比较预测的频谱数据与实际频谱数据的差别,当差别超过预设阈值时,即认为频谱数据中出现异常.
4 实验与分析
4.1 数据集制作及异常仿真
首先,对本次实验使用的数据、仿真异常以及实验条件进行简要说明. 频谱数据来源于亚琛工业大学的开源数据,研究人员在德国亚琛的两个监测点和荷兰马斯特里赫特的一个监测点进行了严格而全面的频谱测量. 监控频段范围为20 MHz 至6 GHz,包括4 个子带,带宽为1.5 GHz,频点分辨率为200 kHz. 在测量中,扫频间隔为1.8 s,即对于监测的每个频点,监测系统每半小时可以获得1 000 个频点的功率谱密度值(PSD),连续监测的最长时间跨度约为14 天[20]. 该数据包含多个常用频带,如GSM900 上行链路(Up Link,UL)频段、GSM900 下行链路(Down Link,DL)频段以及TV 频段等,如图4所示.
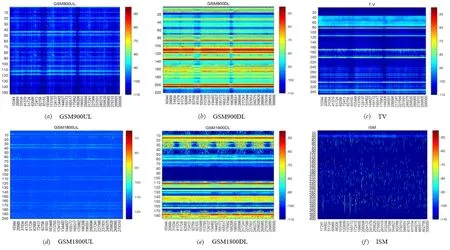
图4 各频段频谱数据图
在大多的异常检测研究中很难获得标准的异常数据,这是因为异常情况往往是小概率且随机出现的,这限制了对实验效果的验证. 为了解决这个问题,本文选择人为地在纯净的电磁频谱数据上增加异常. 本文参考文献[9,13]生成了4 种频谱异常,分别为单个强信号干扰异常、脉冲干扰异常、变频信号干扰异常以及频段阻断干扰异常. 为了检测算法的普适性,增加异常态势的种类,除以上的4 种干扰异常之外,随机任选2 种异常情况进行混合,使异常状态的种类增加到10 种. 以TV 频段(614~698 MHz)数据为例,仿真频谱异常如图5 所示,图中横坐标为频率,纵坐标为频谱采样次数. 本次实验中设计的4 种原始干扰其插入位置、持续时间等因素都是随机的,这提升了异常检测难度. 实际中出现的异常干扰可能持续时间较短,可以通过减少预测频谱时间长度的方法提升算法的检测性能.
需要说明的是,电磁频谱异常种类很多,本文仅对其中的一部分进行了仿真模拟. 本文算法是基于频谱预测的异常检测算法框架实现的,异常的检测依靠的是实际频谱与预测频谱的差别. 因此,理论上不论是何种异常,无论这种异常是否在仿真模拟的异常情况内,只要实际频谱与预测频谱差别超过阈值,算法即判别这种频谱状态为异常状态.
4.2 实验验证
本文构建网络模型融合深度特征,实现了频谱数据的高效预测,在此基础上完成了频谱异常数据的检测. 在多个频段进行实验验证,主要通过以下3 个实验证明了算法性能的优越性. 对比算法包括循环神经网络(RNN)、长短时记忆网络(LSTM)[21]、卷积长短时记忆网络(ConvLSTM)[22]、向量自回归模型(VAR)、卷积神经网络(CNN)[23]. 其中,VAR 是AR 模型的一种变体,适用于多维数据的预测;RNN,LSTM,ConvLSTM 和CNN 均为深度学习中的经典模型,并已被证明具有一定的异常检测性能.
在实验中,设置RNN,LSTM 和ConvLSTM 这3 种算法隐藏层数均为128层,CNN含有3个卷积核为32的卷积层. 计算机配置:CPU 为Inter(R)i7-8750H,GPU 为NVIDIA GeForce GTX 1660,使用Python作为编程语言,利用Keras深度学习框架实现各网络.
4.2.1 在多个频段研究算法异常检测性能
由图3 可知,各频段数据数值范围不同、随时间变化不同,除基本的频谱数据趋势外还包含大量的周期变化点及杂波. 数据的分布会对预测模型的训练以及频谱异常的检出率产生影响,本文旨在提出一种通用的有效的频谱异常检测算法,因此需要在多个频段进行实验,综合评估算法性能. 本实验在GSM900UL,GSM900DL,GSM1800UL 和TV 共4 个频段对4 种模型进行实验. 设已知时间步长为m=80,预测时间步长为k=40,包含频点数为n=160,固定信号干扰功率比SIR=5 dB,共生成训练样本2 000 个,测试样本1 000个. 其中包含仿真异常数据的测试样本为400个.
由于降低判别门限提升预测精度会带来虚警率上升的问题,本文主要使用接收者操作特征曲线(Re⁃ceiver Operating Characteristic Curve,ROC)及ROC 与坐标轴X围成的面积(Area Under Curve,AUC)2种指标评价算法异常检测性能. 各频段异常检测ROC 曲线如图6~9所示,AUC如表1所示.
由图6~9以及表1可知,在进行实验的4个频段中,本文提出的基于融合深度特征的异常检测算法均取得了最优性能,说明在本文模型适用于多个频段,具有一定的通用性. 其中,在GSM1800 UL频段AUC 面积为1,即可实现在无虚警情况下的异常频谱的正确检测. 这是因为该频段数据较为纯净,预测模型精度较高,异常频谱数据更容易检测. 在TV 频段各算法差别较小,这是因为该频段数据含多个信号且频谱数据波动性较强,此时预测频谱与实际频谱差别相对较大,部分正常频谱更易被认为是异常频谱,检测难度变大,但本文算法依然有最优的性能. 在GSM900 DL 频段,本文算法相比于其他算法具有更大的性能优势,相比于LSTM 模型AUC 面积提升约4.5%. 通过对比可以发现,除GSM900 DL 频段CNN 网络性能低于VAR 模型,其他深度学习模型在各频段的异常检测性能均优于VAR 模型,说明了深度学习模型更适用于本文研究的问题. 此外,LSTM 也表现出了不错的异常检测性能,这是因为其拥有强大的数据处理能力,这也是选用该模块构建本文算法的原因.

表1 各频段异常检测AUC表

图6 GSM900UL频段异常检测ROC

图7 GSM900DL频段异常检测ROC
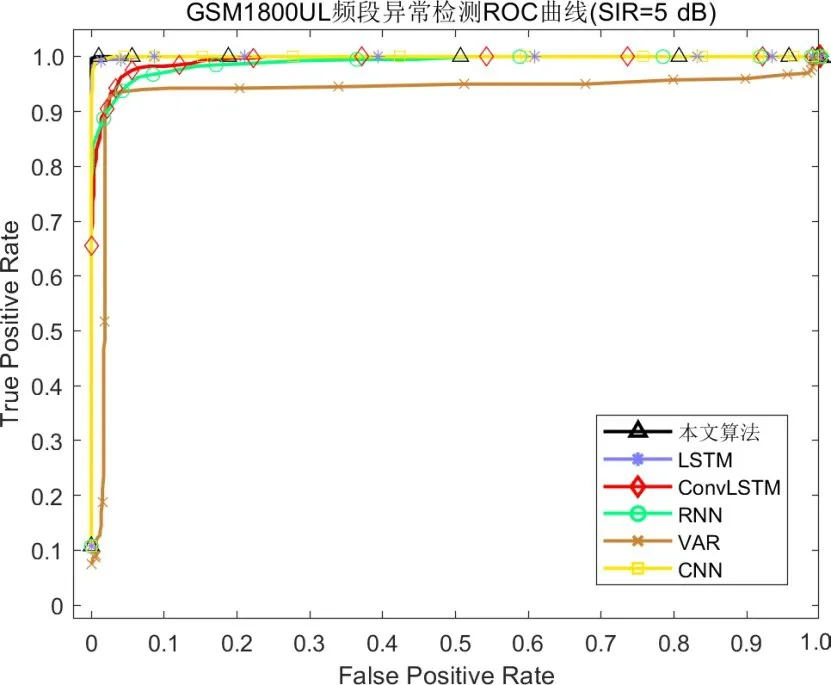
图8 GSM1800 UL频段异常检测ROC
为进一步研究算法性能,对模型的计算量进行分析,各模型参数量如表2所示. 由表2可以看出,在本文研究的5 种深度学习模型中,参数量最少的是CNN 模型,参数量最多的是ConvLSTM 模型. 由于本文算法的模型由LSTM及CNN组合而成,因此本文模型参数量略大于LSTM 模型及CNN 模型参数量的总和,但远小于ConvLSTM模型的参数量.
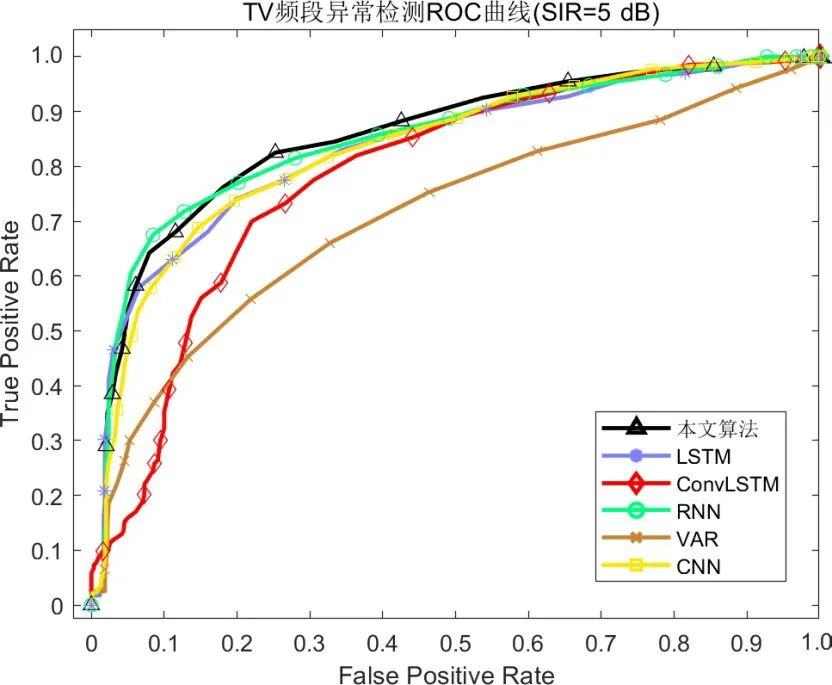
图9 TV频段异常检测ROC

表2 各模型参数量
上述对实验结果的分析体现了本文模型的性能优势,相比于其他基于深度学习的算法模型,本文算法使用多层卷积模块结合LSTM 模块,能够提取不同层次、结构的深度特征,拥有更好的特征提取能力,能够更为有效地在不同频段实现频谱数据异常检测.
4.2.2 不同信干比下的频谱异常检测性能
改变干扰异常数据的强度,研究不同信干比下的异常检测性能. 在GSM900DL 频段、GSM1800DL 频段和TV 频段对算法性能进行实验,实验中信干比分别取-10 dB,-5 dB,0 dB,5 dB 和10 dB. 本文算法在不同信干比下的ROC 曲线如图10~12 所示,ROC 曲线对应AUC 如表3 所示. 对比算法为LSTM 网络,其在不同信干比下的ROC 曲线如图13~15 所示,ROC 曲线对应AUC如表4所示.

图10 本文算法GSM900DL频段异常检测ROC曲线
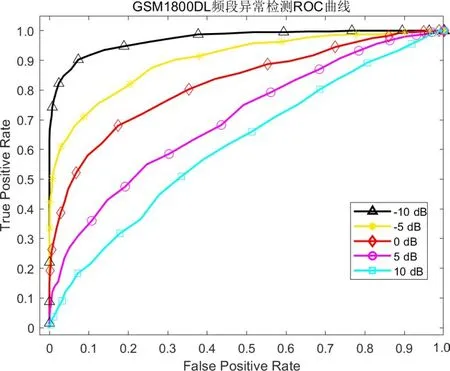
图11 本文算法GSM1800DL频段异常检测ROC曲线
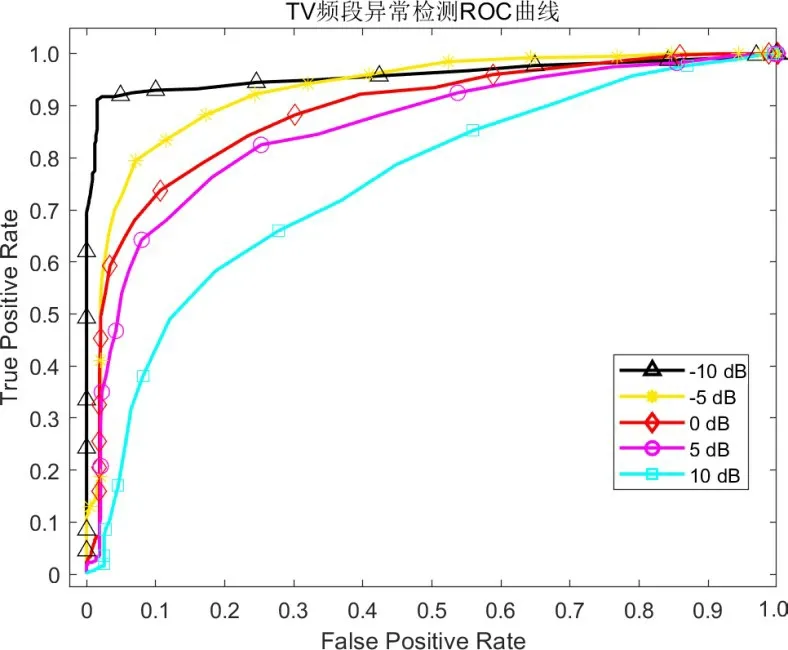
图12 本文算法TV频段异常检测ROC曲线
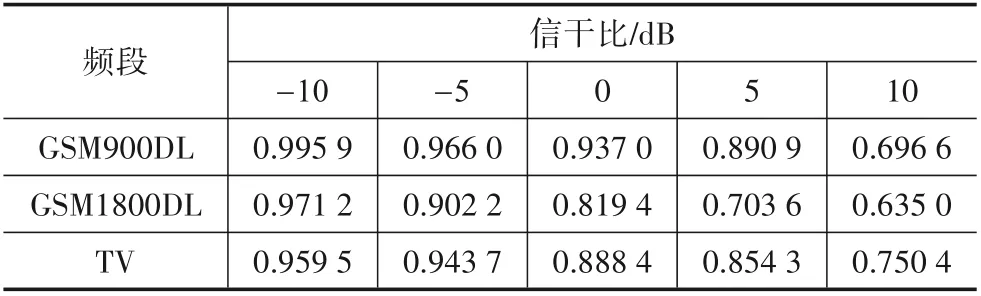
表3 本文算法不同信干比下AUC值
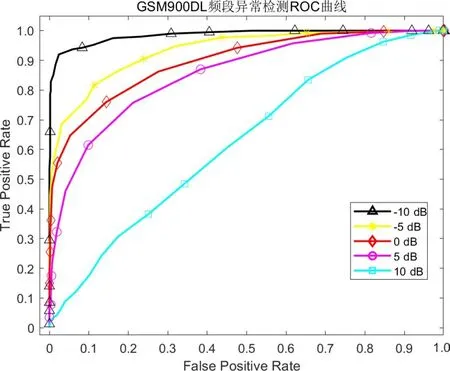
图13 LSTM网络GSM900 DL频段异常检测ROC曲线
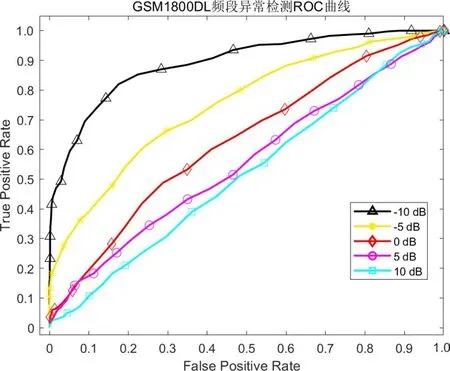
图14 LSTM网络GSM1800 DL频段异常检测ROC曲线
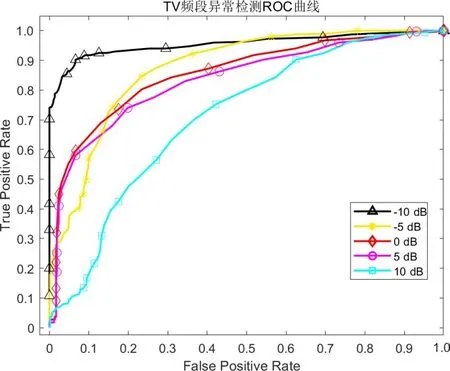
图15 LSTM网络TV频段异常检测ROC曲线
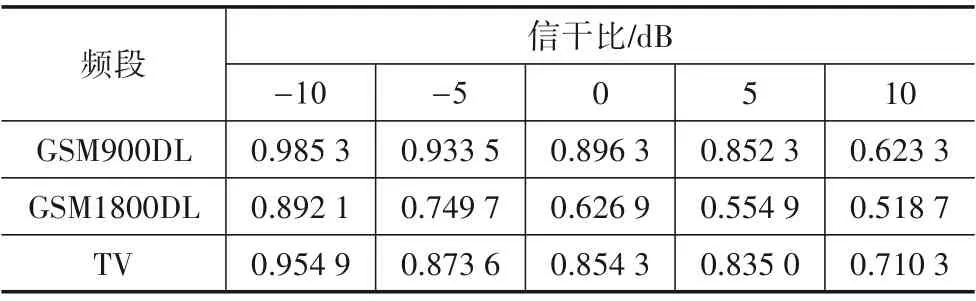
表4 LSTM网络不同信干比下AUC值
对图10~15以及表3、表4进行分析可知,随异常数据强度增大、即信干比不断减小,算法异常检测精度不断提升. 异常干扰的存在的时间长短、带宽以及出现的频点位置都会对算法的异常检测性能产生影响. 在低信干比的环境下,异常存在时间长、能量大,异常干扰对频谱数据的改变明显,检测难度小. 随信干比的增大,异常存在的时间变短、能量变弱,部分异常干扰可能会淹没在强信号频谱内. 短时间的异常以及窄带宽的异常干扰使真实频谱与预测频谱差别很小,检测难度较大,这是造成信干比增大时异常检测性能下降的主要原因. 在GSM1800DL 频段算法性能受信干比影响较大,相比于LSTM 网络,本文算法检测性能更加高效,AUC 提升均高于8%. 当信干比为-10 dB 时,此时干扰强度较大,频谱异常状态分辨难度较小,本文算法的AUC 值均达到了0.95 以上,能够高效地实现异常状态的正确检测. 当信干比为10 dB时,此时异常信号的能量较小,异常状态已经很难通过观察的形式分辨,但在TV 频段本文算法AUC 仍高于0.75,具有一定的异常检测性能. 总的来说,相比于LSTM 网络,本文算法更为高效,性能受信干比强度影响相对较小.
4.2.3 模型参数对检测性能的影响
为体现网络结构的合理性,改变模型参数,探索模型参数变化对异常检测算法性能的影响. 在GSM900UL 频段、GSM900DL 频段进行实验,实验包括6个模型:图3中的本文算法模型(卷积核尺寸为32,并联推断层包含3 层卷积模块);更改原模型卷积核尺寸为64的模型;更改原模型卷积核尺寸为16的模型;去除原模型中LSTM 的模型;并联推断层包含4 层卷积模块的模型;并联卷积层包含2 层卷积模块的模型. 固定信号干扰功率比SIR=5 dB,各模型异常检测性能的ROC 和AUC如图16、图17和表5所示.

表5 各模型异常检测AUC值

图16 各模型GSM900UL频段异常检测ROC曲线

图17 各模型GSM900DL频段异常检测ROC曲线
本文在仿真异常数据以及制作电磁频谱异常检测数据集的基础上,通过以上3个实验分别探究了算法性能. 首先,在多个频段验证了本文算法具有一定的通用性;接着,探究了信干比对算法性能的影响;最后,探索了模型参数对算法性能的影响,证明了本文算法网络结构的合理性. 实验结果表明,本文提出的融合深度特征的频谱异常检测算法性能良好,异常检测精度高. 从网络结构上分析,本文算法提取数据的多层深度特征相比于仅使用对比算法能够获得更多信息. 此外,本文网络模型能够不断融合各层提取特征并进行选择,提升了模型性能.
5 结论
针对电磁频谱异常检测精度不高等问题,本文结合卷积神经网络以及长短时记忆神经网络,提出一种融合深度特征的电磁频谱异常检测方法. 本文算法本质上是一种基于预测的异常检测算法,该算法主要分为频谱预测以及判别检测两个部分. 为实现频谱的高精度预测,首先构建了一个深度特征提取网络. 该网络包含一个能够分级提取深度特征的多级双层CNN 以及一个LSTM,能够通过池化、合并等操作将网络模型提取的各级深度特征进行融合,实现高精度频谱数据预测. 最后,计算预测数据与真实数据的均方误差,判别频谱异常. 在公开频谱数据的多个频段对算法性能进行验证,结果表明本文算法能够有效地实现电磁频谱数据异常检测.

