中心频率与输出端口可重构的新型滤波分支线电桥
朱 旭,杨 健,杨 涛
(1. 中国人民解放军 32802部队,北京 100191;2. 电子科技大学电子科学与工程学院,四川成都 611731)
1 引言
分支线电桥和带通滤波器在无线通信射频前端中被大量使用. 为了缩小电路尺寸,降低电路级联产生的失配损耗,使用集成滤波响应的分支线电桥或称滤波分支线电桥是一个有效的解决手段. 文献[1]和文献[2]分别设计了两款固定工作频率的滤波分支器电桥.为了进一步满足认知无线电对多频多模的应用需求,具有频率调节功能的可重构器件因其具有减小电路体积以及降低设计复杂度的优势,受到了学术界前所未有的关注. 然而,具有频率调节功能的可重构滤波分支线电桥鲜有报道,在文献[3]中,通过使用电长度可控的谐振器,一款频率可调的滤波分支线电桥被成功设计. 然而,电路的插入损耗以及输出平衡度不佳. 除了工作频率的调节,为了进一步拓宽电路的应用场景,提升连接接收机和发射机的匹配电路性能,实现对输出端口的控制十分必要. 文献[4]中给出了一款频率、输出功分比、耦合方向均可重构的分支线电桥设计方案,然而,电路的输出信号幅度平衡度不佳,尤其是工作在反向耦合模式时,信号幅度平衡度较差. 文献[5]中,一款基于CMOS工艺的分支线电桥被提出,电路通过对电容电感进行控制实现输出端口的切换. 通过调研,所有关于输出端口可重构的分支线电桥都没有实现滤波响应的集成,降低了在射频前端中的适用范围. 文献[6]提出了一种频率可调、工作模式可切换的多功能滤波电桥,然而无法实现在滤波分支线电桥工作模式下输出端口的切换.
本文提出了一种集成频率可调、输出端口可切换的滤波分支线电桥设计方法,并基于PCB 工艺完成了电路设计、加工与测试,下面将给出具体的理论分析过程与测试结果.
2 理论分析
图1 给出了所提出的滤波分支线电桥的电路结构图. 电路由4 个半波长阶跃阻抗谐振器R1,R2,R3 和R4构成. 接地的变容二极管D0加载在谐振器的开路端用于频率调节,其中心频率调节原理与谐振器物理尺寸选择可以参考文献[8]中的方法. 背靠背连接的变容二极管Dc1与Dc2加载与相邻的谐振器之间用于控制谐振器的级间耦合,从而实现耦合器输出端口的切换. 变容二极管Dm与固定电容串联后加载于电路的输入、输出端口用来改善阻抗匹配.

图1 可重构滤波分支线电桥结构图
本文提出的滤波分支线电桥的等效电路如图2 所示,其中LC 并联谐振单元用以等效半波长阶跃阻抗谐振器. 等效特性导纳为J1=aY0(其中a>0,Y0为端口导纳)的+90°J变换器用于替代谐振器R1与R2、R3与R4之间的耦合. 等效特性导纳为J1=bY0(其中b<0)的-90°J变换器用于替代谐振器R1 与R4、R2 与R3 之间的耦合. 该电路的输出端口可以在没有外接开关的条件下实现切换. 正向输出模式如图3(a)所示,端口1和端口4 分别为输入端口和隔离端口,端口2 和端口3为输出端口且输出信号具有+90°的相差,即∠S21-∠S31=+90°. 反向输出模式如图3(b)所示,端口1 和端口2 分别为输入端口和隔离端口,端口3 和端口4 为输出端口且输出信号具有-90°的相差,即∠S21-∠S31=-90°.

图2 可重构滤波分支线电桥等效电路
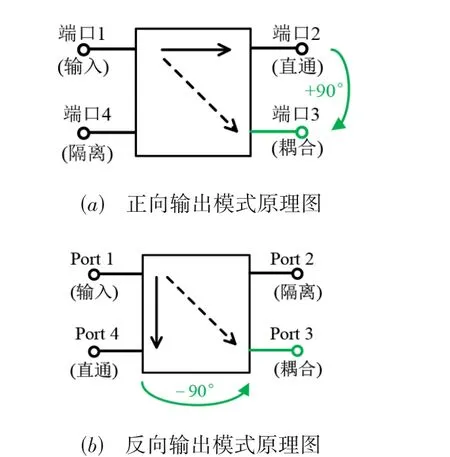
图3 不同输出模式原理图
由于所提出的滤波分支线电桥关于平面PP′和QQ′平面对称,可以通过奇偶模分析法对电路特性进行分析. 与文献[6]中的设计步骤类似,可以计算出可重构滤波分支线电桥的S参数为

其中,k0为给定滤波器指标后根据耦合谐振器理论得出的谐振器级间耦合系数,其综合方法见文献[7]. 本文假设耦合系数的负号对应电感耦合,正号对应电容耦合. 式(2)和式(3)表明耦合系数k12和k34需要保持电容耦合,耦合系数k13和k24需要保持电感耦合. 那么,通过选择合适的耦合系数,满足式(2)和式(3)的条件,所提出的可重构滤波分支线电桥就可以实现输出端口的切换.
为了得出可重构滤波分支线电桥在不同输出端口工作模式下所需要的耦合系数值,可以采用文献[8]中的方法对谐振器间的耦合系数大小进行分析和计算.由于谐振器背靠背排列,并且环形半波长谐振器的中间部位间距较小,谐振器R1和谐振器R4(谐振器R2和谐振器R3)间的耦合由电感耦合主导. 因此,当谐振器间没有加载变容二极管Dc1时,耦合系数k14和k23为电感耦合(k14<0,k23<0). 当加载变容二极管Dc1后,会引入额外的电容耦合用于抵消固有的电感耦合,从而导致级间总的耦合大小随着变容二极管Dc1引入的电容Cc1的增加而减小. 图4(a)给出了谐振器R1 和R4(谐振器R2 和R3)间的耦合系数k14(k23)随电容Cc1在不同谐振器间距s1下的计算值. 可以看出,耦合系数k14(k23)在维持负值的同时,随着Cc1的增加而减小,因此可以通过控制电容Cc1的值,使得耦合系数k14(k23)满足式(2)和式(3).
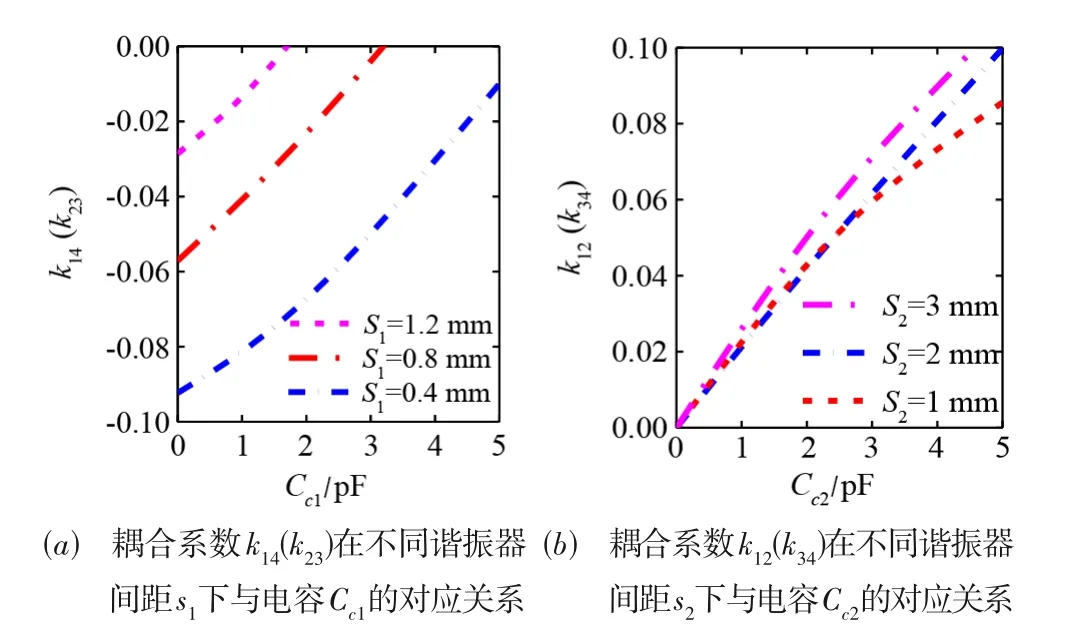
图4 耦合系数与级间加载电容大小的对应关系(谐振器物理尺寸为l1=3.4 mm,l2=8.2 mm,w1=2 mm,w2=0.8 mm)
类似地,谐振器R1 和R2(谐振器R3 和R4)间的耦合由电容耦合主导[8],总的耦合大小会随着由变容二极管Dc2引入的电容Cc2的增大而增加. 图4(b)给出了谐振器R1 和R2(谐振器R3 和R4)间的耦合系数k12(k34)随电容Cc2在不同谐振器间距s2下的计算值. 可以看出,耦合系数k12(k34)在维持正数的同时,随着Cc2的增大而增加,因此可以通过控制电容Cc2的值,使得耦合系数k12(k34)满足式(2)和式(3),从而实现可重构滤波分支线电桥输出端口的切换.
3 仿真与测试
中心频率1.4 GHz、相对带宽5%,波纹系数0.1 dB的准切比雪夫滤波器原型被用于可重构滤波分支线电桥设计. 根据文献[9],初始的二阶带通滤波器的级间耦合系数为k0=0.069,外部品质因数Qe=16.861. 根据式(2)和式(3),在正向输出模式下,滤波分支线电桥所需的耦合系数为k12=k34=k0=0.069,k14=k23=-k0=-0.069;在反向输出模式下,滤波分支线电桥所需的耦合系数为k12=k34=k0=0.069,k14=k23=-k0=-0.098. 为了实现所有端口与50 Ω 匹配,所有输出模式下所需的端口外部品质因数为Qe=16.861. 需要指出的是,外部品质因数可以通过调节变容二极管Dm以及输入/输出抽头的位置l3进行调节,其设计方法可以参考文献[8].
提出的可重构滤波分支线电桥使用厚度为25 mil的Rogers 6010 介质板进行实物加工. 变容二极管D0,Dm和Dc2使用的商用变容二极管型号为MA46H202(Cj=0.7~7 pF),变容二极管Dc1使用的商用变容二极管型号为MA46H201(Cj=0.3~2.2 pF). 6 pF 的集总电容与变容二极管Dm串联用于隔直以及端口匹配. 图5 给出了所设计电路的实物照片,电路尺寸见表1.

图5 可重构滤波分支线电桥实物照片

表1 电路物理尺寸/m
可重构滤波分支线电桥在正向输出模式下(∠S21-∠S31=90°)的S参数仿真与测试结果见图6(a)~(c). 其通带的调节范围为1.2~1.6 GHz,在相对带宽为5%时的插入损耗(|S21|和|S31|)的变化范围为(3+3.2)dB 至(3+2.7)dB. 通带调节范围内的回波损耗(|S11|)和隔离度(|S41|)分别优于15 dB 和13 dB. 图6(d)为正向输出模式下幅度与相位不平衡度测试结果,其中幅度不平衡度在1 dB带宽内优于0.4 dB,所有工作中心频率处的相位不平衡度均优于2°.

图6 正向工作模式下可重构滤波分支线电桥S参数仿真与测试结果(注:相同颜色的测试曲线对应相同的中心频率)
可重构滤波分支线电桥在反向输出模式下(∠S21-∠S31=-90°的S参数仿真与测试结果见图7(a)~(c). 其通带的调节范围为1.2~1.6 GHz,在相对带宽为5%时的插入损耗(|S31|和|S41|)的变化范围为(3+3.3)dB 至(3+2.8)dB. 通带调节范围内的回波损耗(|S11|)和隔离度(|S21|)分别优于15 dB 和12 dB. 图7(d)为反向输出模式下幅度与相位不平衡度测试结果,其中幅度不平衡度在1 dB带宽内优于0.4 dB,所有工作中心频率处的相位不平衡度均优于2°. 两种工作模式均实现了良好的滤波以及分支线电桥性能.

图7 反向工作模式下可重构滤波分支线电桥S参数仿真与测试结果(注:相同颜色的测试曲线对应相同的中心频率)
表2 列出了本工作与其他输出端口可切换分支线电桥的性能对比. 与文献[4]对比,提出的滤波分支线电桥显著提高了输出信号间的幅度平衡度. 同时,本工作是目前唯一实现滤波响应的输出端口可切换分支线电桥. 低Q值的变容二极管导致了加工电路较高的插入损耗,本方案选用的商用变容二极管在该工作频段下的无载Q值约为50,从而导致了电路具有较高的插入损耗. 为了改善电路的插入损耗,可以选用高Q值的变容管(比如MEMS 工艺的变容管,其无载Q值大于200). 这里需要指出的是,运用文献[4]和文献[8]中控制谐振器间耦合系数的方法,本工作可以实现在两种输出模式下输出功分比的调节.

表2 本工作与其余端口可重构分支线电桥性能对比
4 总结
本文提出了一种创新的可重构滤波分支线电桥设计方法,通过改变滤波分支线电桥谐振器之间耦合的性质与强弱实现电路工作频率与信号输出端口的灵活控制. 测试结果显示该电路的中心频率调节范围为1.2~1.6 GHz,正向输出和反向输出时的相差分别为90°和-90°. 验证电路展现了优秀的调节能力与灵活的自由度. 该电路设计方案有望被应用于认知无线电中.

