一种基于深度强化学习的协同通信干扰决策算法

宋佰霖，许 华，齐子森，饶 宁，彭 翔

（空军工程大学信息与导航学院，陕西西安 710077）

1 引言

在通信对抗领域，体系对抗、协同干扰已成为主要作战运用方式，如何调配干扰资源、在最大程度上提高资源利用率是当前亟须解决的重要难题，给指挥决策带来巨大挑战. 一些基于博弈论［1］、随机理论［2］等方法的认知无线电干扰［3］决策研究取得了一定进展，这些研究通过设置干扰双方对抗场景，推导博弈收益函数，计算干扰样式、功率等干扰参数来得到最优干扰策略. 此类方法虽能输出较好结果，但适用场景较为简单，无法满足当前多维协同的战场环境，与实际作战使用仍有较大差距.

近年来，基于人工智能技术的认知电子战相关研究取得了较大突破，智能干扰决策是其中关键一环，一般采用基于深度强化学习技术实现智能决策. 深度强化学习是一种通过智能体与环境交互、神经网络拟合输出动作方案、环境反馈引导网络训练更新、使评价收益值最大的一种机器学习方法，能够在无先验信息或先验信息较少的情况下通过交互学习给出较优的决策结果，广泛应用于战场资源优化［4］、指挥协同控制［5］等军事智能领域. 在通信干扰决策方面，文献［6］建立多臂赌博机模型，建立误码率曲线字典，通过字典采样并经过算法计算，干扰机可以构造出与实际曲线相似的误码率曲线，在3 次交互作用下学习最优干扰策略；文献［7］同样应用多臂赌博机模型，通过决策干扰信号样式、数据包发送指令以及功率等级等物理层参数，得到最高效功率分配的干扰方案；文献［8］为解决强化学习算法在干扰决策中收敛速度慢的问题，通过等效参数建模，降维干扰参数选择搜索空间，加入以往的干扰经验信息，在缩短系统学习时间的同时输出最佳干扰策略；文献［9］基于整体对抗思想提出基于自举专家轨迹分层强化学习的干扰资源分配决策算法（Bootstrapped expert trajectory memory replay-Hierarchical reinforce⁃ment learning-Jamming resources distribution decision-Making algorithm，BHJM），能够在干扰资源不足的条件下优先干扰威胁等级较高的跳频通信目标，并输出资源利用率最高的干扰方案. 然而以上研究都是针对某种信号体制或单个干扰站给出优化后的干扰方案，无法解决协同干扰决策及资源分配问题.

本文为解决协同电子战的干扰决策问题，首先构建“整体优化、逐站决策”的协同决策模型，为算法提供决策环境；而后基于深度强化学习，在Actor-Critic 算法架构下提出一种融合优势函数的协同干扰决策算法（Advantage Function based Collaborative Jamming Decision-making algorithm，AFCJD），优化干扰资源分配方案；此外，在奖励函数中引入专家激励机制［5］，提高算法的探索能力，使算法能够更快收敛并输出更优的干扰方案；最后，仿真实验结果表明，本文算法给出的干扰方案能够实现对干扰资源的最优利用，并大幅提高决策效率.

2 系统模型

图1 所示为一个典型地空通信对抗场景，敌方由一架预警机指挥多架歼击机执行突防任务，干扰方在多个阵地上分布式设置干扰站，意在通过协同配合破击敌方通信体系. 跳频通信作为抗干扰能力较强的通信手段，是干扰方实现较好干扰效果需要突破的重点和难点问题. 跳频通信通常采用频分方式进行组网，通过在不同网间规划多个跳频频率集以起到抗干扰通信的战术目的. 干扰方通常采用拦阻干扰、梳状谱干扰、灵巧干扰等手段压制跳频信号，其中梳状谱干扰使用最为广泛，通过将能量集中在多个干扰谱内，实现对跳频频点的精准压制，同时达到对己方通信影响最小的目的. 假定在准确侦察到敌通信信道频率规划和使用信息的情况下筹划干扰方案，侦察分析已对侦收到的跳频信号进行分选，区分不同信道信号，提高干扰的精准程度.

图1 典型干扰场景

判断跳频信号是否被成功干扰，一般从空域、频域、能量域3 个角度入手，假定当干扰频率覆盖跳频频率集1/3 以上频点，且干扰波束内存在目标、干扰功率满足干信比压制条件时，可认为干扰有效. 忽略收发天线不同带来的极化损失，干信比计算方法可用式（1）表示［9］.

其中，PJ为干扰机的发射功率；PS为信号发射机的发射功率；HJ为干扰机发射天线与接收天线增益之积；HS为信号发射机发射天线增益与接收天线增益之积；LJ和LS分别为干扰信号和通信信号传输的空间损耗，用式（2）表示，R（km）为信号传播距离.

将式（2）代入式（1）中，可得到干信比的一般计算表示方法，如式（3）所示.

当使用梳状谱干扰时，能量集中在各个干扰谱带内，不考虑带外能量损失，干信比的计算方法如式（4）所示，当干信比大于目标压制系数时，可认为干扰有效.

在体系电子战中，干扰资源的不同调配会对整个体系的干扰效果产生不同影响. 例如部署在不同位置的干扰站针对同一目标的干扰可获得不同干扰效果，或当某一干扰站能同时干扰多个目标时，干扰不同目标也会对其余资源的任务分配产生影响，所以协同干扰的难点就在于如何将多个站的干扰资源合理调配，使其发挥最大干扰效能. 当干扰站对准多个目标时，实际中通常按照目标的威胁等级来分配干扰任务，为简化场景，以站与目标间距离远近来评判目标的威胁等级，距离越近威胁越大，距离越远威胁越小，即在对准多个目标的情况下，干扰站优先干扰距离最近的目标. 本文从干扰站的部署位置及干扰目标入手，预先设置可选阵地，通过改变各干扰站的干扰方向角实现对目标的选择，每个干扰站的部署位置及干扰方向角可称为其干扰方案，利用算法的训练优化输出资源利用率最高的干扰方案.

3 融合优势函数的协同干扰决策算法

3.1 算法模型构建

深度强化学习通常研究智能体与环境交互输出动作，得到环境反馈的奖励值，进而不断优化动作策略的过程，该过程是序贯决策的且具有马尔可夫性，一般将其称为马尔可夫决策过程（Markov Decision Process，MDP）. 基于深度强化学习方法研究干扰决策问题，首先需要将干扰决策建模为MDP 模型. 干扰决策实质上是针对当前目标信息给出最优干扰方案，需把这一静态优化场景转化为MDP 具有“交互-执行-反馈-环境变化”特点的动态决策过程. 协同决策通常包括逐站决策和多站同时决策两种模型，一方面逐站决策模型适用于强化学习交互、反馈的动态过程，每一个干扰站决策后，环境反馈的奖励值直接反映出该站决策的效果；另一方面当干扰站数量较多、决策维度较大时，多站同时决策模型会难以收敛，而逐站决策模型可通过基于全局最优的奖励函数设计实现整体优化，受决策维度影响小，决策效率更高，因此在本文要解决的问题中，逐站决策模型更加适用. 模型工作流程如图2所示.

图2 模型工作流程

本文构建“整体优化、逐站决策”的协同决策模型，将每个干扰站都作为独立的智能体，通过同一决策网络分步、顺次决策干扰动作，该动作包括干扰站的部署位置及干扰方向角；当某个智能体决策完毕后，执行其干扰动作，并将因执行干扰动作而改变的目标信息输入下一个智能体；采用集中式训练的方法从整体优化干扰方案，当所有智能体决策完毕后，训练更新决策网络的权值参数，直至收敛. 定义模型所需基本元素如下.

（1）状态空间：假设某个目标跳频信号未被干扰的频点数量为h，定义状态空间S=[h1,h2,…,hn]，即表示所有目标跳频信号未被干扰的频点数.

（2）动作空间：定义决策网络输出动作为A，表示干扰站的布设阵地及干扰方向角对应的干扰动作编码，如表1 所示. 为降低算法的决策维度，在0°～180°范围内每15°可选择一个角度作为干扰方向角，可选角度共有11个.

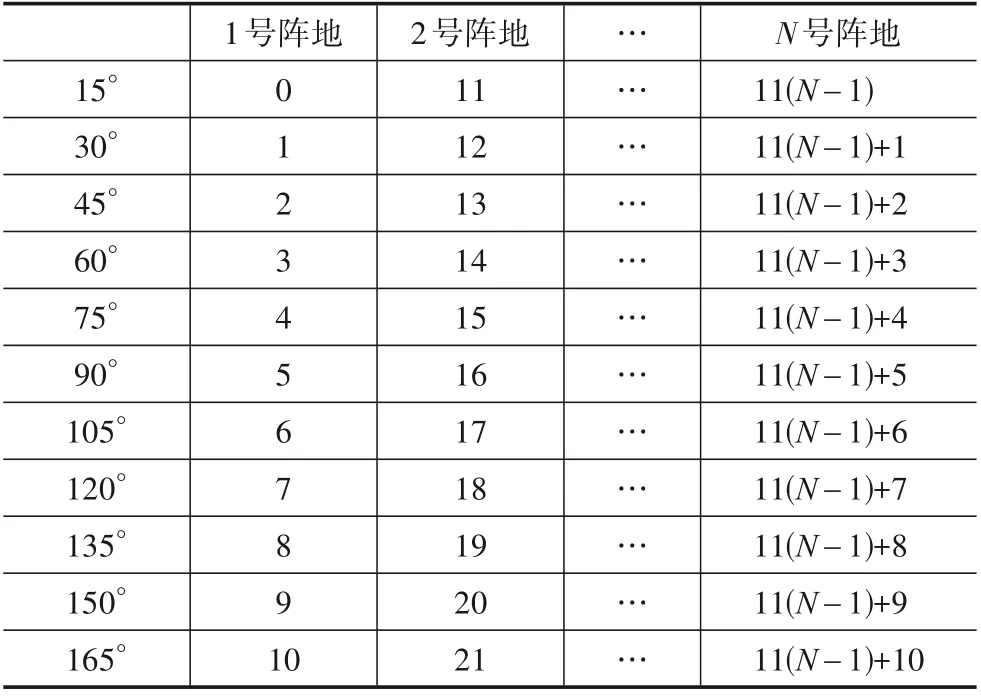
表1 干扰动作编码表

部署阵地D和干扰方向角L可用式（6）和式（7）表示.

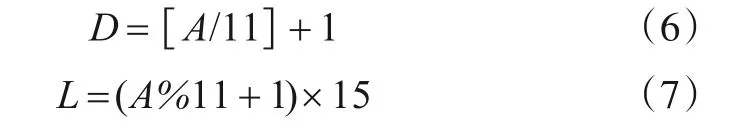
（3）奖励函数：基于全局最优思想设置奖励函数，用于表示整体干扰方案的优劣程度. 当所有跳频信号全部被干扰时，奖励值r为80；当干扰波束内无任何目标时，r为-15，否则r为0.

在强化学习问题中，一般只根据是否完成回合任务或回合输赢来判定奖励值，但这样会产生稀疏奖励问题［10］，导致决策算法难以收敛. 本文对奖励函数进行改进，把专家激励嵌入奖励函数［5］中，在基础奖励值rbase（式（8））上加入一个额外的专家激励值rexp（式（9）），使得rexp能够不断引导智能体朝着r累积值最大的方向更新策略；将rbase与rexp数值相加，即为嵌入专家激励后的r值.rexp为后续决策形成专家式引导，并对当前决策形成内部激励，Ncha表示已被干扰的目标数量，Njam表示当前干扰站成功干扰的目标数量，Ncha值不同，得到的rexp值也不同，Ncha越大，表明其越接近干扰全部目标，rexp值越大，获得的r（式（10））值也越大. 由于获得更大r值是智能体的学习目标，所以当越接近干扰全部目标时，rexp值的激励作用越强，从而形成对智能体决策的专家引导.

每次决策网络输出干扰动作后，根据环境给出的反馈奖励值训练更新网络的权值参数，待当前方案可将全部目标干扰时或干扰资源用尽后该回合结束.

3.2 融合优势函数的协同干扰决策算法

本文提出融合优势函数的协同干扰决策算法（AFCJD），该算法采用Actor-Critic 架构，包括策略执行网络即Actor 模块、价值评估网络即Critic 模块、奖励评估模块、优势函数计算模块和训练优化模块，具体计算流程如图3所示.

图3 AFCJD算法流程图

策略执行网络感知环境状态，获取各目标频点数信息St，通过网络的拟合运算输出干扰站的干扰动作At，不同的网络参数表示不同策略. 价值评估网络估计当前策略的优劣程度，输出状态St下干扰动作At的价值V(St)和V(St+1)，代表策略执行网络的更新目标.

奖励评估模块内嵌奖励函数，针对执行干扰动作引发的状态改变给出评价，即计算输出奖励值r. 算法中引入优势函数A(St,At)［11］，用于表示状态St下执行某一动作对应的价值V(St)相对于价值平均值的大小. 通过将价值归一化到平均值上，将输入策略执行网络的数据控制在一定范围内，有助于减小方差，提高学习效率. 计算式如下：

训练优化模块对策略执行网络和价值评估网络参数进行训练优化，定义损失函数如下：

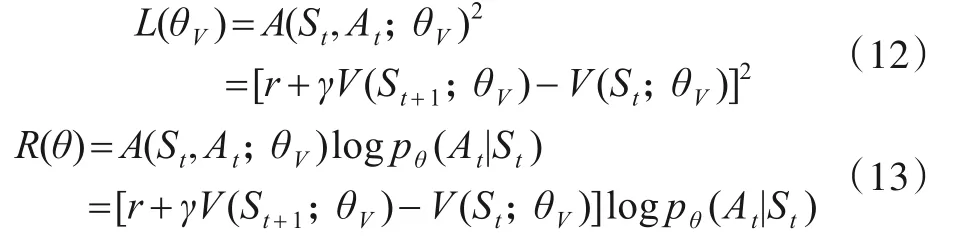
式（12）中L(θV)表示价值评估网络的损失函数，通过训练不断提高网络对价值评估的精准程度，给策略执行网络更精确的训练目标；式（13）中R(θ)表示策略执行网络的损失函数，根据价值评估网络输出的A(St,At；θV)优化网络参数，使网络决策出更优的干扰动作.

AFCJD 算法如算法1所示，算法中策略执行网络和价值评估网络中的隐藏层均使用全连接神经网络，策略执行网络的输出层使用Softmax函数以及价值评估网络输出层无激活函数外，其余激活函数均为ReLU函数.

4 实验与仿真

为评估本文所提AFCJD 算法的性能，将其与DQL（Double Q-Learning）算法［12］、DDNN（Deep Deconvolu⁃tional Neural Network）算法［13］进行对比. DQL 算法、DDNN算法在文献［12］用于抗干扰通信场景中，可将其类比转化为协同干扰决策算法应用在本文模型中. 同时，通过对比AFCJD 算法与无专家激励奖励机制算法的决策效果，来评估专家激励奖励机制对于算法决策性能提升的优势作用.

4.1 场景及参数设置

算法1 AFCJD算法(1)初始化策略执行网络和价值评估网络,权值参数分别为θ和θV;(2)设J为干扰站数量,W为仿真总回合数;for k=1,2,3,…,W do:for k=1,2,3,…,J do:(3)获取环境状态St,即各个目标信号的跳频点数;(4)策略执行网络给出干扰动作At,计算其阵地位置及干扰方向角;(5)执行干扰动作,按式(4)计算干扰效果;(6)计算奖励值r;(7)获取环境状态St+1;(8)价值评估网络估计St的价值V(St)及St+1的价值V(St+1);(9)按式(14)更新价值评估网络参数;(10)按式(15)更新策略执行网络参数;if 目标全部被干扰或干扰资源用尽:(11)Break;(12)当算法训练至最优后,循环结束

根据通信侦察及各类情报，获取当前空域内20 个待干扰目标，用坐标形式粗略表示其空域位置；共使用6个跳频波道，跳频点数分别为30，65，130，65，30，130，具体参数情况如表2 所示. 根据长期情报或侦察情报，干扰方已知每个通信目标的信号发射功率为200 W.

表2 侦察目标信息

现预设6 个阵地，其坐标为［100，336］、［40，182］、［65，219］、［30，565］、［70，425］、［100，456］，共有30个干扰站可供使用，每个干扰站的最大干扰功率为50 kW，最多干扰20 个跳频频点，干扰站及待干扰目标的位置分布如图4所示.

图4 干扰站及目标位置示意图

AFCJD 算法的参数设置如表3所示，为使算法更好收敛，将学习率设置成梯次变化的形式，表中JS为每300 回合的干扰成功率. 当JS大于0.8 时，降低神经网络的训练频率，每10 步训练1 次Actor 网络，每50 步训练1次Critic网络，降低算法收敛到局部最优的概率.

表3 算法参数设置

4.2 干扰资源利用对比分析

若某一回合决策出的干扰方案可将全部目标信号干扰，则认为该方案干扰有效. 用每300 回合的平均方案有效率来表示干扰成功率，当干扰成功率达到100%时认为算法收敛至最优，训练结束. 首先对比3 种算法的干扰成功率，为提高算法的探索利用效率，可将DQL算法和DDNN算法的可用干扰站数量提升至35个.

从图5 中可以看出，本文提出的AFCJD 算法收敛最快，在14 000 回合左右平均成功率可达100%，而DDNN 算法和DQL 算法只能在30 000 回合左右收敛至接近100%的干扰成功率. 从干扰成功率的对比可以得出，本文提出的AFCJD 算法收敛最快，能够在最少的仿真回合内给出可用的干扰方案.

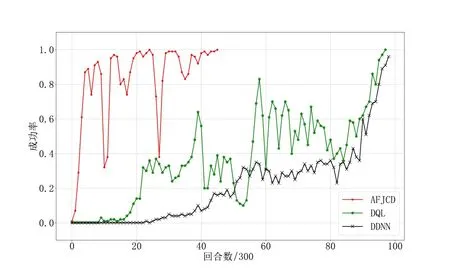
图5 干扰成功率对比

取3 种算法每300 回合的平均奖励值进行对比，如图6 所示，可以看出本文提出的AFCJD 算法从开始训练起奖励值即较大，在不断训练过程中逐渐增大至算法收敛停止训练，训练趋势与干扰成功率的趋势相似.而其他2 种算法训练初期的平均奖励值较低，前1 000个回合的均小于0，说明在训练初期算法的性能较差，无法输出有效方案；与干扰成功率的训练趋势相似，随着训练深入，2 种算法的平均奖励值不断增大，决策能力逐渐增强，直至算法收敛. 从平均奖励值的对比可以看出，本文AFCJD 算法的决策能力提升较快，决策效率较高，较DDNN算法和DQL算法提高50%左右.

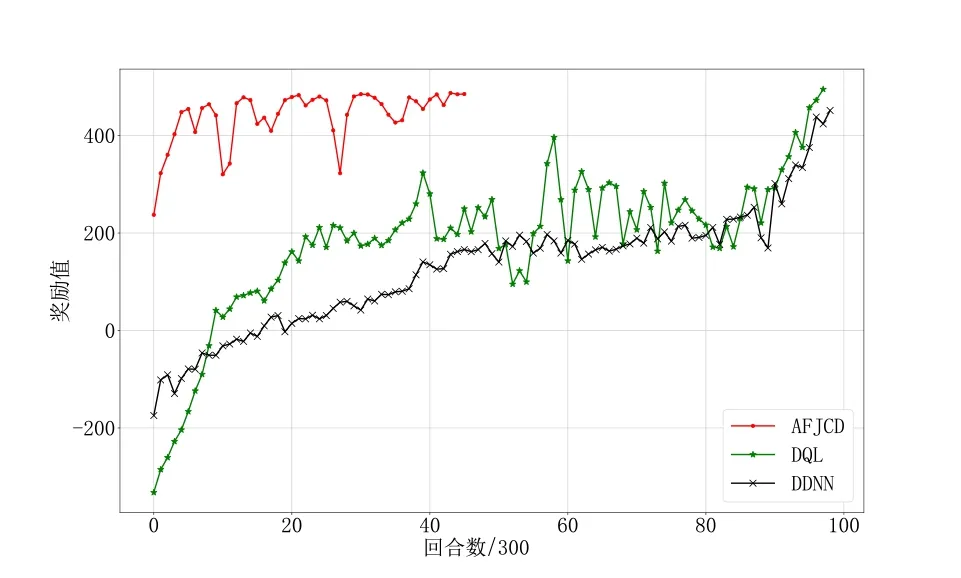
图6 平均奖励值对比

此处加入基于规则的决策算法进行对比，该算法不依靠任何智能计算方法，按照干扰动作编号顺次给干扰站分配干扰动作. 若该动作经过计算满足式（4）的条件，则动作有效并执行；否则顺次选择下一动作，直至出现有效动作. 当全部目标可被干扰时，各站干扰动作的组合即为干扰方案.

计算每300 回合内所有有效干扰方案所需干扰站数量的平均值，对比不同算法给出方案所需干扰站的数量如图7 所示. 从图7 中可以看出，基于规则的决策算法给出的干扰方案大约需要28个干扰站能够将所有20 个目标全部压制；而DDNN 算法和DQL 算法收敛后需要大约26 个干扰站可将20 个目标全部压制，本文提出的AFCJD 算法收敛后只需要大约25 个干扰站即可压制全部目标. 可以看出，使用智能算法后可以得到节约干扰资源的干扰方案，且本文AFCJD 算法决策速度更快，决策效率远高于另外2种算法.

图7 干扰站数量对比

随着训练进行，干扰方案也会不断优化，但干扰站数量的平均值无法体现最优干扰方案的资源利用情况，图8 反映了4 种算法决策出的最优方案所需干扰站数量的对比情况. 其中，AFCJD 算法最少只需要24 个干扰站即可压制全部目标，相比于DDNN 算法和DQL算法能够提高8%的资源利用率. 相比于基于规则的决策算法，AFCJD 算法能够提高15%的资源利用率，由于基于规则的算法无智能计算环节，所以AFCJD 算法的优势更为明显，这也说明基于智能算法的协同干扰决策方法能够达到一般算法所达不到的决策效果.

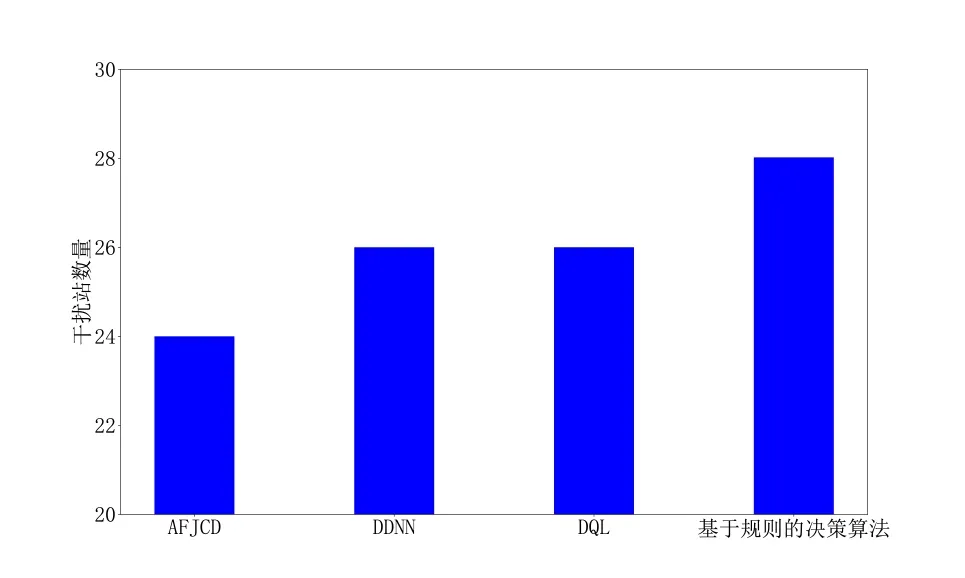
图8 最优干扰方案对比

综上所述，本文提出的AFCJD 算法相比于DDNN算法和DQL 算法更快收敛到最优干扰方案，决策效率提高50%以上；且最优方案的资源利用率更高，能够节约8%的干扰资源，所以AFCJD 算法对于协同干扰决策的效果更好.

此外，本文提出的AFCJD 算法是一种on-policy 算法，能够直接利用决策网络的输出动作及环境的反馈奖励训练网络；DDNN 算法和DQL 算法属于DQN 一类的off-policy 算法，需要将每一次决策的状态、动作等参数作为样本存入经验池，再从经验池采样训练决策网络，off-policy一类算法的采样效率直接决定了算法的有效性及训练效率. 通过上述对比还可以推断出，AFCJD这种on-policy 算法在干扰决策背景下相比off-policy 一类算法具有更高的决策效率.

4.3 嵌入式专家激励奖励机制对决策结果的影响分析

嵌入式专家激励奖励机制本质上也是一种奖励工程，文献［10］已经证明过这种内部激励能够突破算法本身的训练边界，给智能体更多探索环境信息的空间，提高算法的决策效率. 本文通过对比AFCJD 算法与无专家激励奖励机制算法的决策效果，来说明专家激励奖励机制对于增强算法决策性能的优势作用. 无专家激励奖励机制算法的奖励函数与式（8）相同，当所有跳频信号全部被干扰时，奖励值r为80；当干扰波束内无任何目标时，r为-15，否则r为0.

如图9、图10所示，在前6 000个回合两种算法的训练趋势相同，无论是平均干扰成功率还是平均干扰站数量均在不断收敛且效果相当，6 000 回合以后AFCJD算法继续收敛直至平均干扰成功率达到100%. 无专家激励奖励机制的算法在6 000 回合以后收敛速度下降，在18 000 回合成功率达到90%并在较大范围内振动，无继续收敛趋势. 图11 所示为无专家激励奖励机制算法的奖励值变化情况，可以更清晰地看出算法的训练趋势，在18 000 回合后算法由于探索能力相对较弱无法再决策出奖励值更高的结果，并且出现了一小段过拟合现象.

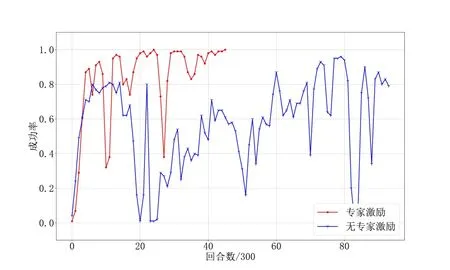
图9 干扰成功率对比

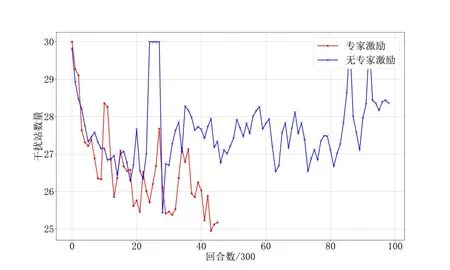
图10 干扰站数量对比

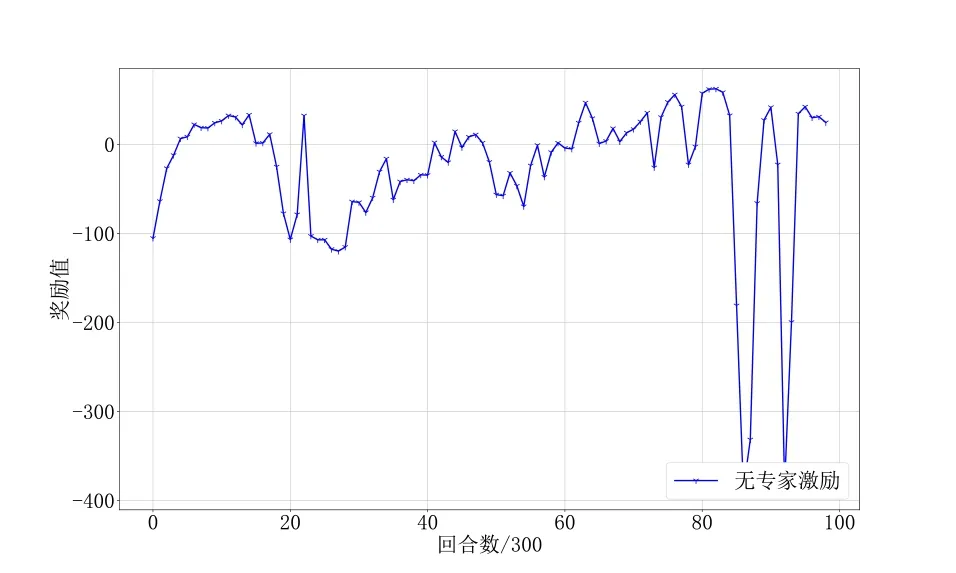
图11 奖励值

综上所述，相比无专家激励奖励机制的算法，AFCJD 算法具有更强的探索能力，能够输出更优的决策结果，训练收敛较快且更稳定. 同时可以得出，嵌入式专家激励奖励机制能够提高算法的探索能力，提高算法的决策能力并提高算法的决策效率.

5 小结

本文针对协同电子战中的跳频通信干扰协同决策难题，通过构建“整体优化、逐站决策”的协同决策模型，基于深度强化学习提出一种融合优势函数的协同干扰决策算法（AFCJD），并在奖励函数中引入专家激励机制，进一步提高算法性能，使算法能够给出针对现有目标资源利用率最高的干扰方案，并大幅提高决策效率. 仿真结果表明，AFCJD 算法能够决策出干扰资源利用率最大的干扰方案，相比于现有智能决策算法，给出的干扰方案能够节约8%干扰资源，决策效率提高50%以上；在引入专家激励奖励机制后，AFCJD 算法具有更强的探索能力，训练收敛较快且更稳定.