一种基于VMD-PSO-SVM的短期风电功率预测算法
黄 峰,向书琛,王 睿,贾任远,游 红
(1.湖南工程学院 电气与信息工程学院,湘潭 411104;2.湖南省高校风电装备与电能变换协同创新中心,湘潭 411104)
0 引言
随着煤炭、石油等不可再生资源的减少,以及环境污染问题的日益加重,清洁能源的开发和利用逐步引起各国政府的关注.作为典型的可再生能源,风能易于获取且技术成熟,到目前为止,风力发电在生产中已经得到了大规模的应用.
近年来,在碳中和、碳达峰的大背景下,我国风力发电技术取得快速发展,风力发电装机容量持续增加.截至2021 年7 月底,全国发电装机容量已达2.9 亿千瓦,同比增长34.4%.由于风力发电主要受风力波动性的影响,而风力具有不确定性,造成风力发电功率不稳定,影响并网安全[1].风电功率预测能保证风电并网安全[2].
风电功率预测研究经历了从物理方法到统计学方法再到人工智能的发展过程.目前风电功率预测大致分为两个方向,一是基于空间相关性[3]和数值天气预报[4]的机理驱动法,主要是利用物理信息分析风速特性,但是这类方法不能充分利用历史数据[5-6],预测精度较低.二是利用时间序列模型、概率模型或机器学习模型,从历史数据确定学习模型参数,将模型应用到预测上的模型驱动法.随着计算机算力的提升,数据采集、存储难度下降,大大降低了模型驱动法的门槛,使得模型驱动法能广泛地应用在生产过程之中.
模型驱动法可以分为四类:概率统计模型、机器学习模型、深度学习模型和模态分解.深度学习模型利用多层神经网络构造非线性函数,对应着复杂的假设空间,神经网络函数具有强大的模型拟合能 力 . 其 中 Long short-term memory,LSTM[7]、Gate Recurrent Unit,GRU 特别适合对序列数据建模.Convolutipnd Neural Network,CNN、Deep Belief Nets,DBN 等深度学习方法[8]已经广泛应用在电力系统中[9].模态分解考虑序列数据的线性和非线性影响因素,将序列分解为线性部分和非线性部分,分别建立线性模型和非线性模型,再将两部分的预测结果组合.
由于风电功率的时间序列复杂,影响因素多.需要对原始数据进行预处理后再建立模型.可采用基于信号处理的方法,先将风电功率序列分解为多个信号,分别对每个信号建模,最后用各个信号的预测值进行重构,获得原序列的预测值,设计组合预测方法[10].组合预测方法效果优于单一预测方法[11-12].
变分模态分解(VMD)是把相似的功率数据分解成一系列相对稳定的子信号,突出数据的局部特征信息,VMD 采用非递归形式、变分模态分解处理原始数据,提高了模型的抗干扰能力和鲁棒性.
本文提出一种基于VMD-PSO-SVM 的风电功率预测模型.VMD 选取合适的收敛函数,能把原数据分解为较少的子数据,降低建模的复杂性,接着利用PSO(粒子群优化)算法优化SVM(支持向量机)预测模型,用来预测VMD 分解后的各分量,最后对各分量预测值求和,获得风电功率预测值.
1 变分模态分解
变分模态分解(VMD)是一种新颖的复杂信号分解技术,其作用是将原始信号数据分解成若干具有不同中心频率的有限带宽模态信号.通过迭代查找变分模型的最优解.其本质是构造及求解变分问题[13-14].
首先,构造变分问题,假设原始信号f可分解为k个分量,保证分解序列为具有中心频率的有限带宽的模态分量.其约束变分表达式如式(1)(2)所示:

式中:uk为模态信号,f 为时间序列,k 为模态数,*为卷积运算符.wk为第k 个模态的中心频率,δ(t)为狄拉克函数.
其次,通过拉格朗日乘子λ 将变分问题转变成非约束性问题,方便求得变分约束模型的最优解,得到增广拉格朗日表达式如式(3)所示[15]:

式中:α 为二次惩罚因子,λ 为拉格朗日乘子.
利用交替方向乘子法,优化得到uk和wk,同时寻找(3)式的“鞍点”,其为(1)式中的最优解.通过交替更新后得到的表达式如下.分别为:

式中:ε 为收敛判据,N 为最大迭代次数.
VMD 迭代求解过程如图1 所示.

图1 VMD迭代求解过程图
2 支持向量机
支持向量机(SVM)结构简单,鲁棒性好,是一种基于统计学习理论的机器学习算法.一般采集非线性数据作为样本对支持向量机进行训练[16],由于超平面对非线性的数据很难进行分类,需要进行化简.通过核函数可将非线性的样本空间映射到高维线性空间进行分类,找出最佳分割超平面,实现非线性到线性的转化[17].
具体过程如下,回归函数[18]f(x)为:

式中,w 为权值向量,b 为常数,w 和 b 的最小化由下式来进行估算:

约束条件为:

式中,C 为惩罚因子,ξi、ξi*为松弛因子,ε 为损失函数.
由于特征空间属于高维度空间,实际应用一般采用Lagrange Multiplier Method 求解高维二次规划问题:

约束条件为:

式中,xi、xj为输入量,yi为输出量,ai和 bi为拉格朗日乘子.
3 粒子群算法PSO
粒子群算法(PSO)初始化为一群随机粒子在D 维空间解上通过追踪当前最优粒子搜索的最优值,通过对其参数反复调整和试验,可以在一定程度上规避局部最优解的问题,从而寻找全局最优解.具有收敛速度快、精度高等优点[19].
PSO 是在持续的迭代中寻找最优解,假设D 维搜索空间里由n 个粒子组成的种群,粒子的速度、位置及粒子的最优位置分别设为v、x 和p,第i 个粒子可以看作D 维向量,有:

第i 个也可以视为D 维向量,有:

则第i 个粒子的个体极值为:

全部粒子的全局极值为:

粒子速度及位置更新的公式如(17)(18)式:

式中,n 为种群规模;ω 为惯性权重;Vij为粒子i经过第j 次迭代中对应的速度;rand()∈[0 ,1 ];xji为粒子i 在第j 次迭代中对应的位置;c1和c2为加速度因子;gbest为群体最优值;pbest为粒子i的个体最优值.
4 PSO-SVM预测模型
PSO-SVM 预测风电功率的主要思想是随机产生一个惩罚因子C 和核函数g,并将它作为粒子群的初始位置,再使用PSO 搜索最优SVM 参数,从而对风电功率进行预测.具体流程如图2 所示.

图2 PSO-SVM算法流程图
5 VMD-PSO-SVM 预测模型
由于通过VMD 分解原始数据得到的固有模态函数IMF 相对稳定,使用稳定的信号进行预测,其结果通常会优于原始信号.因此,在进行风电功率预测时,对风电功率进行VMD 分解,将得到的数据再进行PSO-SVM 预测,再对每组预测值进行组合,建立VMD-PSO-SVM 组合预测模型,此方法能进一步提高预测精度,达到更好的预测效果.
建立预测模型步骤如下:
(1)通过VMD分解原始风功率输入信号,将其分解成若干稳定的固有模态函数IMF和趋势项.
(2)采用PSO-SVM 模型分别对每个IMF 和趋势项进行预测,获得精度更高的预测结果.
(3)对每组分量的PSO-SVM 预测结果进行重组,得到的预测结果更接近于原始数据.
(4)通过误差分析,用来对比新旧模型预测的性能,评估新模型是否合格.
预测模型流程如图3 所示.
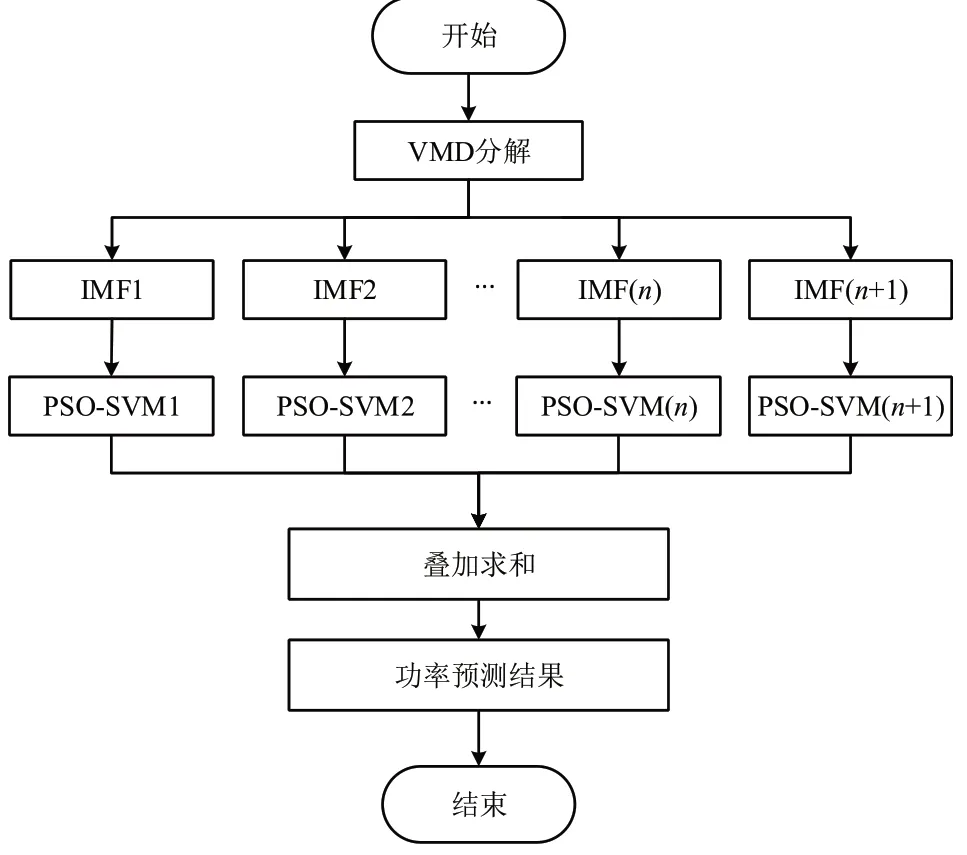
图3 VMD-PSO-SVM预测流程图
6 仿真分析
以哈电风能有限公司大板梁风电场22号风机为研究对象,进行仿真分析,采样时间间隔为15 min,共200 个采样点.选取前160 个采样点作为预测模型训练集,后40 个采样点作为测试集进行滚动预测,预测时间30 min.对历史数据预处理后的风电功率如图4 所示.
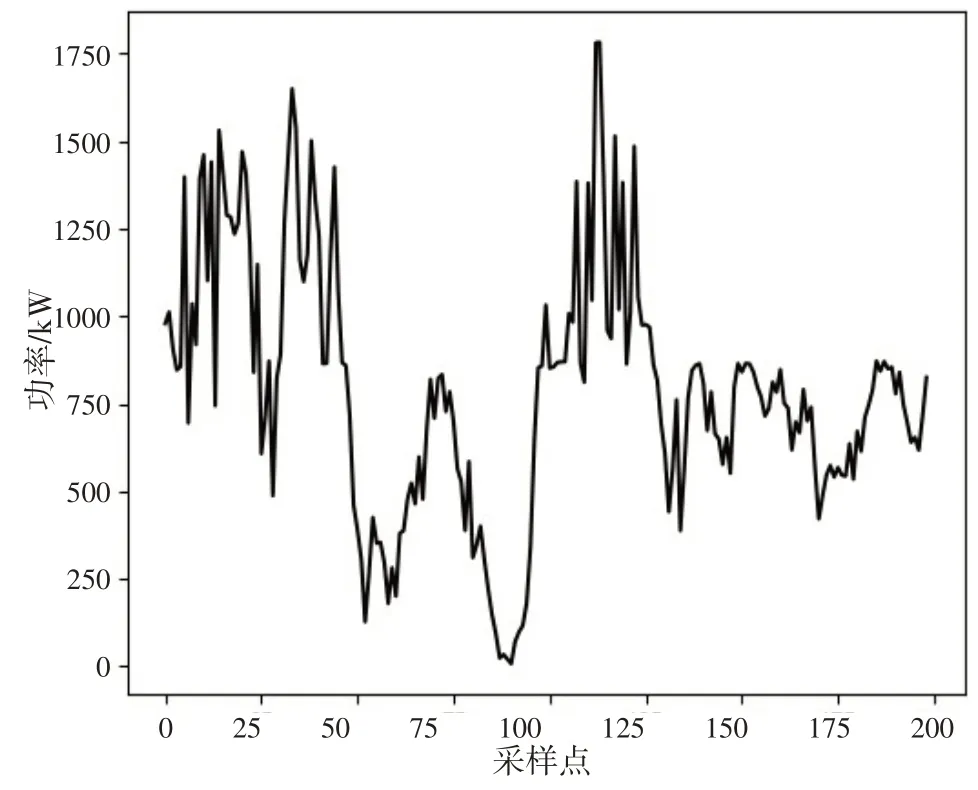
图4 原始功率曲线图
利用VMD 对其进行分解,结果如图5 所示.

图5 VMD分解原始功率数据图
图5 中第一个图形是趋势分量,反映原始风力发电量的整体变化趋势;IMF1 是细节分量,反映了原始风力发电量序列在不同细节上的变化趋势;IMF2~IMF5 为随机分量,反映了原始风力发电量的随机性.从图5 可以看出,这几个分量都很稳定,分量值均匀分布在零两侧,这些分量在预测时,预测误差将会非常小.
以预处理后的风电功率序列输入,分别建立SVM、PSO-SVM、VMD-PSO-SVM 预测模型,对其进行误差分析.对各个模型预测结果分别与实际功率值进行对比.如图6 所示.

图6 各模型预测值与实际值对比
通过对比模型实际值与预测值可知,VMDPSO-SVM 预测结果相对SVM 模型、PSO-SVM模型,预测曲线与实际值吻合度更高,且PSOSVM 模型的预测值比SVM 模型预测值更加接近真实值.将这三种模型的EMAPE和ERMSE对比分析,如表1 所示.

表1 各模型误差对比分析表
7 结论
本文提出一种基于VMD 的PSO-SVM 短期风电功率预测算法.测试结果表明:(1)将VMD 算法分解后的结果与原始风电功率作对比,其功率分量更加稳定;(2)对分解后的功率各个稳定分量分别建立PSO-SVM 模型,并以粒子群算法对SVM 算法进行参数寻优,可以降低风功率波动性对预测精度的影响;(3)基于 VMD-PSO-SVM 的组合预测模型能提高预测精度.

