考虑非线性结电容的SiC BJT模型改进

孙 静，熊 伟，谢 斌，陈山源

（湖南工程学院 电气与信息工程学院，湘潭 411104）

0 引言

碳化硅（SiC）材料具有宽禁带、高临界击穿电场和高热导率等优良特性，被广泛应用于高电压、高功率开关器件中［1-2］.在基于SiC 材料的多种功率器件中，SiC 双极结型晶体管（BJT）因具有低导通电阻、高开关速度、低温度依赖性、强短路能力和不存在二次击穿等特性，而成为功率开关应用中的一种可行器件，特别适合应用于高温环境下［3-4］.国内外学者对SiC BJT进行了大量的研究［5-9］.Balachanddran 等［5］建 立 了 SiC BJT 的 传 统 Gummel-Poon（GP）模型，然而传统GP 模型存在许多不足，如未建立准确的温度模型、未考虑准饱和区的准饱和效应、SiC/SiO2界面复合效应以及基极-发射极（B-E）结电容和基极-集电极（B-C）结电容不连续等.考虑到准饱和效应，Y.Huang等［6］在电路仿真软件SABER中建立了SiC BJT 的GP 模型，但该模型未考虑温度以及 SiC/SiO2界面复合效应的影响 .Johannesson 等［7］在PSpice 中建立了1200 V/800 A 的4H-SiC BJT行为模型，该模型考虑了温度的影响，并研究了杂散电感、基极电阻、器件内部建模参数、载流子寿命、发射极掺杂等对开关损耗的影响，但该模型未考虑SiC/SiO2界面复合效应对电流增益的影响.Patrzyk 等［8］建立了包括自热现象的电热模型，并采用了与温度相关的本征载流子浓度模型来模拟准饱和效应，但未考虑SiC/SiO2界面复合效应以及B-E 结电容和B-C 结电容不连续等问题.Liang等［9］提出了一种改进的 SiC BJT 的 PSpice 行为模型，该模型考虑到了SiC/SiO2界面复合效应以及温度的影响，但未考虑电容不连续问题.在设计功率器件及其产品过程中，非线性问题对器件和系统的稳定性具有十分重要的影响［10］.SiC BJT 的动态特性受到其非线性结电容的影响.因此，在建立SiC BJT 的行为模型时需要考虑非线性结电容对器件性能的影响.

本文基于表面复合Gummel-Poon（SRGP）模型，提出了一种考虑非线性结电容的SiC BJT 改进模型.该模型考虑了准饱和效应、SiC/SiO2界面复合效应以及B-E 结电容和B-C 结电容不连续等问题.改进模型并利用受控源来等效非线性电容，在满足准确性的同时，提高了模型的收敛性.希望本工作能为SiC BJT 功率器件的实际应用提供一定的参考.

1 模型

1.1 SRGP模型

SiC BJT 结构图和SRGP 模型如图1 所示.

图1 模型结构图

描述SiC BJT 模型电流方程如下［11］：

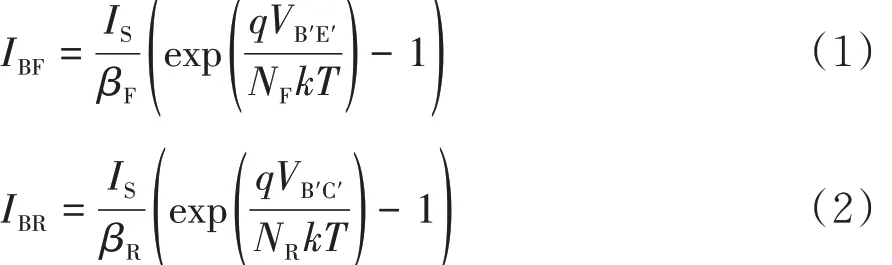
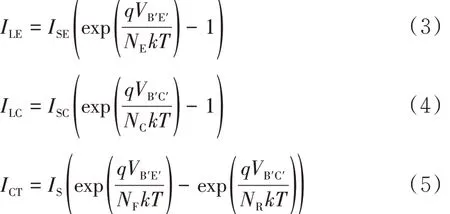
式中，IBF和 IBR分别为 SiC BJT 的正向和反向基极电流，ILE和ILC分别为SiC BJT 发射极漏电流和集电极漏电流，ICT为集电极电流，IS为饱和电流，ISE为 B-E 结 漏 饱 和 电 流 ，ISC为 B-C 结 漏 饱 和 电流，VB'E'是基极和发射极端子之间的内部端子电压，VB'C'是基极和集电极端子之间的内部端子电压，βF和βR分别是理想的最大正向和反向电流增益.NF和NR分别是正向和反向电流发射系数，NE和NC分别是B-E 结泄漏发射系数和B-C 结泄漏发射系数 .q 是基本电荷（1.602×10-19C），T 是温度，k 是玻耳兹曼常数（8.617×10-5eV/K）.

为了描述正向有源区和饱和区之间准饱和区的准饱和效应，对集电极电阻RC建模如（6）式［6］：

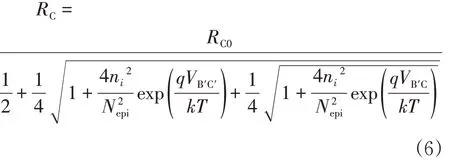
式中ni是本征载流子浓度，Nepi是外延层集电极掺杂浓度，VB'C为基极内部端子与集电极外部端子之间的电压，RC0是零偏压集电极电阻.

在较低集电极电流密度下，SiC BJT增益系数主要受空间电荷区中载流子复合的影响.而在高集电极电流密度下，SiC BJT 的增益系数会因为受到SiC/SiO2界面复合效应的影响出现显著下降［12-13］.为了考虑SiC/SiO2界面的复合效应，在基极与发射极间添加一个二极管DSR，该复合电流Irec方程如（7）式［11］：

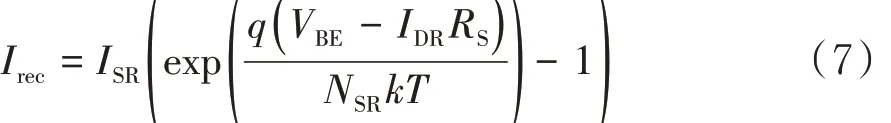
式中ISR是附加二极管的饱和电流，RS是附加二极管的串联电阻，NSR是附加二极管的发射系数，VBE是 B-E 端偏压 .

1.2 改进模型

为了考虑非线性结电容的影响，本文在SRGP模型的基础上提出SiC BJT 改进模型，如图2 所示，其中B-E 结电容和B-C 结电容用受控源来等效.

图2 Sic BJT改进模型

一般情况下，B-E 结和B-C 结都没有严重的正向偏压，因此非线性结电容以势垒电容为主，建立电容方程如（8）（9）式：

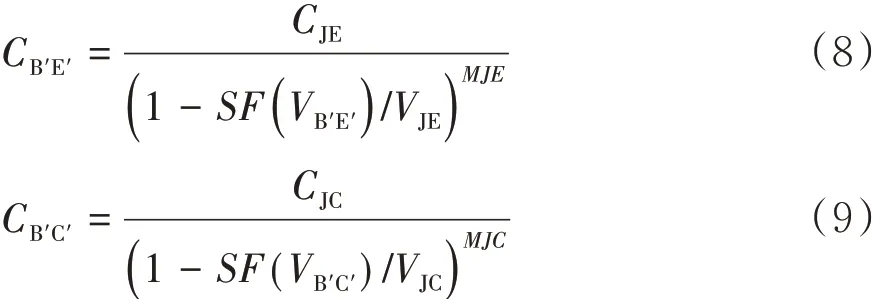
式中CJE和CJC分别为零偏压时B-E 结和B-C结的电容，MJE 和 MJC 分别为 B-E 结和 B-C 结的梯度因子，VB'E'和 VB'C'分别为 B-E 和 B-C 的内建电势.其中函数SF（VB'E'）和SF（VB'C'）为开关作用函数，其表达式如（10）（11）式：

由于CB'E'和CB'C'在正、反偏置下的电容方程不同，通过设置开关函数SF（VB'E'）和SF（VB'C'）可减少电路支路，同时避免了使用压控开关，减少电路节点，从而提高模型的收敛性［14］.本文将可变电容模型等效为受控电流源［15-16］，如图2 虚线框中所示.让可变电容的电压加在电容值为1 F 的C0电容上，那么1 F 电容上的电流值可写为电压微分方程：

2 模型验证

为了验证所改进模型的有效性，本文选取Gene-SiC 公司研制的GA10JT12-247 型号（1200 V/10 A）的 SiC BJT 为研究对象，提取相关参数［9］，其中电容参数如表1 所示.本文的模型参数均为300 K 温度状态下的数值.

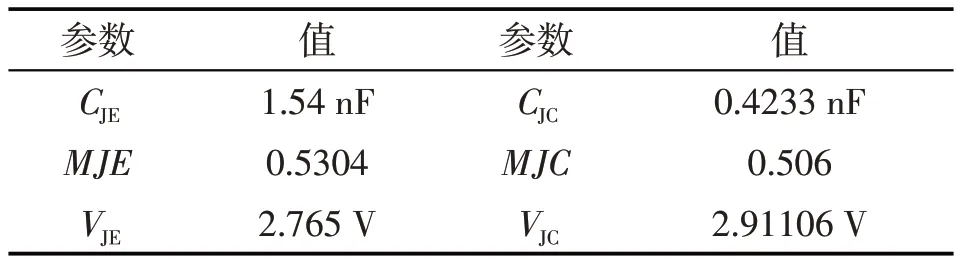
表1 电容参数

图 3 显 示 了 B-E 结 的 CBE-VBE曲 线 和 B-C 结的CBC-VBC曲线，从图3 中可以看出，模型仿真的C-V 曲线与实验得到的C-V 曲线基本吻合，说明所提取的电容参数以及电容方程准确可靠.

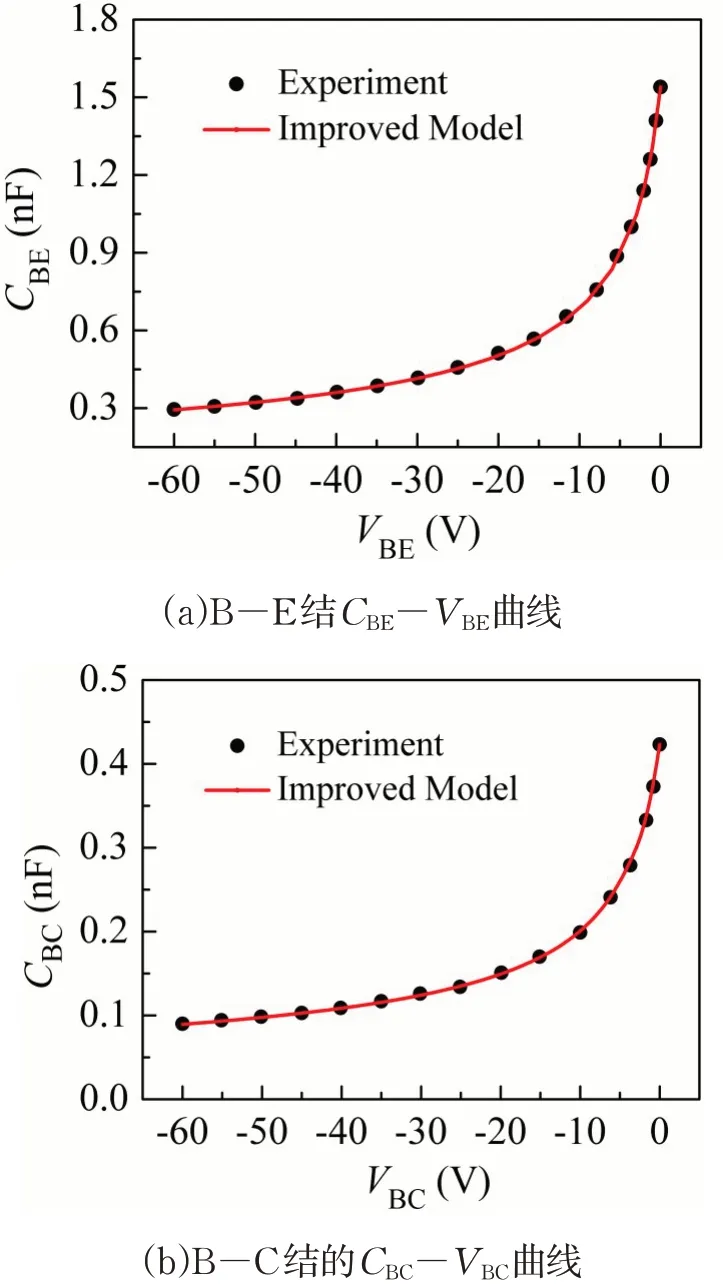
图3 两结曲线图

本文在PSpice 软件中搭建了SiC BJT 的改进模型.该模型由电阻、电容、二极管以及受控源等装置来实现，如图4 所示.

图4 PSpice软件中SiC BJT改进模型实现原理图

对SiC BJT 的静态特性和动态特性进行了仿真，并与实验结果进行了对比.图5（a）显示了300 K 温度下的转移特性曲线IC-VBE.从图中可以看出，VBE达到2.7 V 左右后，集电极电流会随着VBE的增加而增大，仿真得到的转移特性曲线与实验所得到的曲线吻合性较好，验证了改进模型的有效性. 在不同基极电流下得到的输出特性曲线如图5（b）所示.

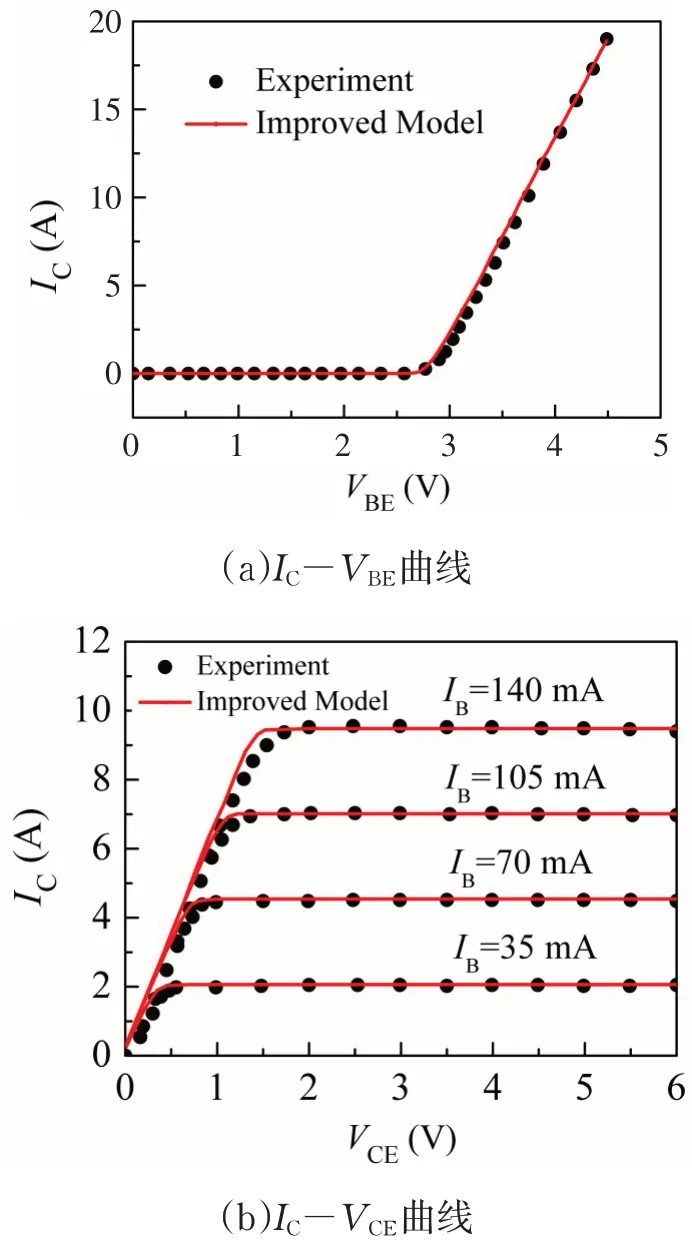
图5 SiC BJT测量和仿真图

从图中可以清楚地看到模型在不同的基极电流下均能准确模拟SiC BJT 的输出特性.仿真结果与实验结果的吻合验证了改进模型的有效性.

为了验证模型在宽电流范围内的有效性，本文比较了仿真和实验得到的不同集电极电流下的正向电流增益，如图6 所示.图6 是在VCE=5 V 和温度为300 K 下得到的结果.从图中可以看到改进模型在较宽的集电极电流范围内与实验得到的电流增益匹配良好，说明在考虑SiC/SiO2界面复合效应后模型可以准确预测不同集电极电流下的正向电流增益.

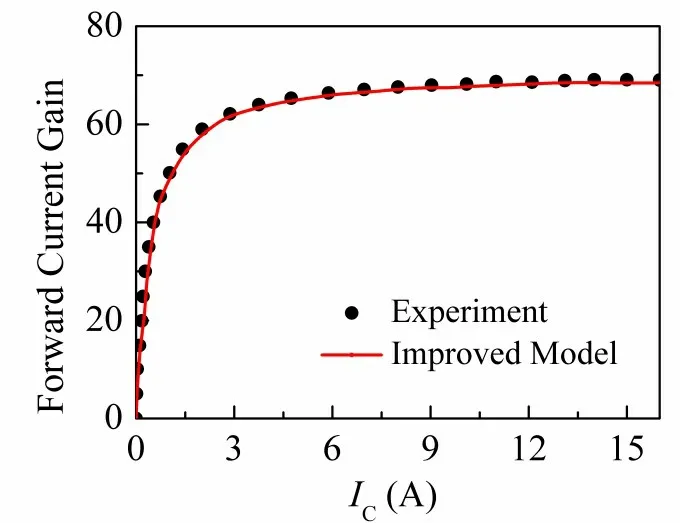
图6 不同集电极电流下的正向电流增益

为了得到SiC BJT 的开关特性，本文使用双脉冲测试电路对SiC BJT 的改进模型进行测试.图7为双脉冲测试电路原理图，双脉冲测试仪主要由SiC BJT、续流二极管和电感组成［17］.本文分别选取了母线电压为600 V 和400 V 两个电压等级，对300 K 温度下实验测量和模型仿真的开关特性进行对比，如图8 所示.从图中可以看出，该模型能够较好地预测SiC BJT 的开关行为，说明考虑了非线性结电容影响的改进模型可有效预测SiC BJT 的动态特性.

图7 双脉冲测试电路原理图

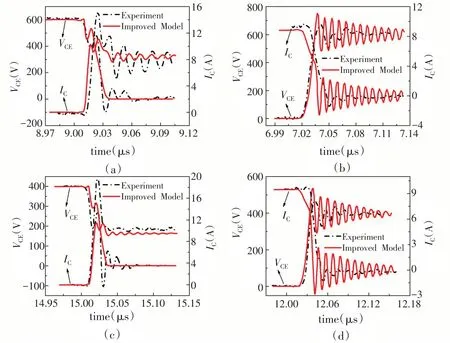
图8 测量和模型得到的在Vdc=600 V下（a）导通（b）关断波形；在Vdc=400 V下（c）导通（d）关断波形

3 结论

考虑SiC BJT 非线性结电容的影响，本文基于SRGP 模型提出了一种SiC BJT 的改进行为模型.该模型通过受控源来对BJT 内部结电容进行建模，解决了结电容的非线性以及不收敛等问题.通过PSpice 软件对该模型进行了仿真，并与实验结果进行了对比，证明了该模型能够准确地预测SiC BJT的静态和动态特性，这对基于SiC BJT 功率器件的电力电子应用具有一定的指导意义.