基于凸优化的燃料电池汽车节能驾驶研究*

魏小栋，刘 波，冷江昊，周星宇，孙 超，孙逢春

（1.湖南大学，汽车车身先进设计制造国家重点实验室，长沙 410082；2.北京理工大学，电动车辆国家工程实验室，北京 100081）

前言

燃料电池汽车作为未来汽车动力可能的终极解决方案之一，具有零排放、高能效、大里程等电动车无法比拟的天然优势。同时，在智能化、网联化技术快速发展的背景下，汽车具备了人、车、路、云等信息交互的功能。基于汽车的动力系统特性，实现融合交通信息的节能驾驶，能够大幅度提升车辆的能效。

在燃料电池汽车能量管理的研究中，林歆悠等为提高燃料电池汽车的能效，结合等效氢耗最小策略，通过控制电能消耗速度，建立了行驶里程自适应的控制策略。Min 等基于神经网络和遗传算法，提出一种考虑燃料电池启停的能量管理策略，使启停次数降低33%。Quan等考虑燃料电池性能退化成本，提出基于速度预测的模型预测控制策略，讨论了速度预测对能量管理策略的影响，并通过硬件在环测试验证了策略的实时性能。王骞等考虑燃料电池的寿命和经济成本，提出基于模糊逻辑控制的能量管理策略。此外，有些研究学者根据燃料电池汽车动力系统的特性，提出基于凸优化的能量管理策略，仿真表明，基于凸优化控制策略在保证结果近似最优的同时，具备更快的计算速度。

在多信号灯场景车速规划的研究中，Sun 等考虑了交通信号灯配时的不确定性，系统提出了传统燃油车通过多个信号灯节能车速规划的鲁棒控制方法，仿真表明，通过牺牲不到5%的到达时间，就可以显著降低车辆的燃油消耗。冷江昊等基于纯电动汽车的能耗模型，结合动态规划（DP）和内点法快速求解车速规划问题，降低了电动车的能耗。Wei 等提出一种燃料电池汽车车速规划和能量管理的联合优化方法，基于双层DP 求解最优车速，利用交替方向乘子法（ADMM）实现能量管理，仿真表明，该方法计算速度相对较快，而且具备一定的节能效果。Guo 等采用分层控制方法将燃料电池汽车通过多信号灯的车速规划问题解耦为两个子问题，以此减少计算时间，简化混合优化问题。凸优化方法同样适用于求解车速规划问题，Huang 等通过拟合燃油发动机的油耗曲线，构建了求解车速规划的凸问题，并运用序列凸优化算法降低了车辆的油耗和行驶时间。

节能驾驶技术是通过优化整车行驶速度，降低智能网联车辆行驶过程中的实际能量需求，提高车辆通行的整体能效。能量管理则是针对给定车速工况的燃料电池汽车（电电混合）和混合动力汽车（油电混合），实现车辆动力系统中各能量源输出功率的合理分配，提高动力系统效率，降低车辆能耗。在智能网联燃料电池汽车上，节能驾驶能够为能量管理提供最优车速轨迹，而且能量管理能够在最优车速轨迹的基础上实现更深层次的节能效果。但节能驾驶和能量管理问题的计算量均较大，很少有人针对两者开展联合研究。为打破计算壁垒，实现联合优化，本文创新性地提出基于分层凸优化的燃料电池汽车通过多信号灯场景的快速车速规划和能量管理方法。

图1 为本文提出的分层凸优化方法的整体架构。在上层中，首先计算车辆在不同速度下匀速行驶的耗氢量并绘制静态氢耗图。基于静态氢耗图，利用DP计算车辆匀速行驶的最优路径，选定该路径下通过的绿灯周期为最优绿灯窗口，划出窗口的上下边界形成最优行驶路径的搜索区域。以车辆总需求功率最小为优化目标，建立求解车辆加速度的凸二次规划问题，最后利用OSQP 计算出车辆最优行驶路径及最优车速轨迹。在下层中，基于最优车速轨迹，构建以最小能耗为优化目标且符合ADMM 算法的能量管理问题，利用ADMM 算法快速完成燃料电池发动机和动力电池之间的功率分配。

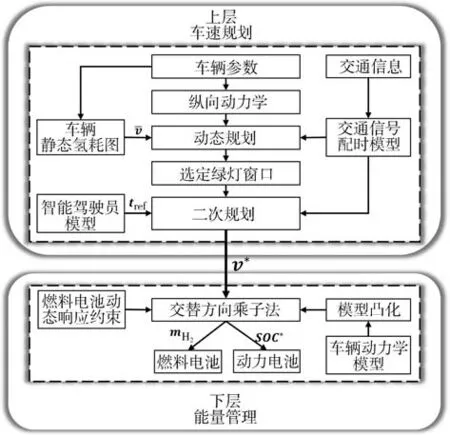
图1 分层凸优化方法的架构

1 建立模型

本章介绍车辆动力系统结构、动力系统凸模型和信号配时模型。

1.1 动力系统结构

本文的研究对象为一款燃料电池汽车。车辆的动力系统结构如图2 所示，由燃料电池发动机和动力电池共同为车辆提供能量。

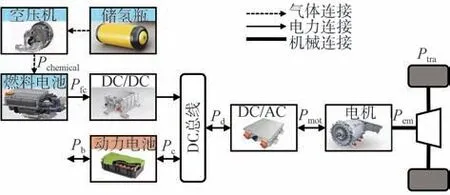
图2 燃料电池汽车动力系统结构图

从图中可以看出，燃料电池发动机将氢氧电化学反应产生的化学能转化为电能进行输出。动力电池将自身化学能转换为电能进行输出。两动力源输出的电能在直流总线上形成耦合功率，再通过DC/AC 把电能传递给电机，电机将电能转换为机械能以满足车辆驱动的需求功率。车辆的主要技术参数见表1。

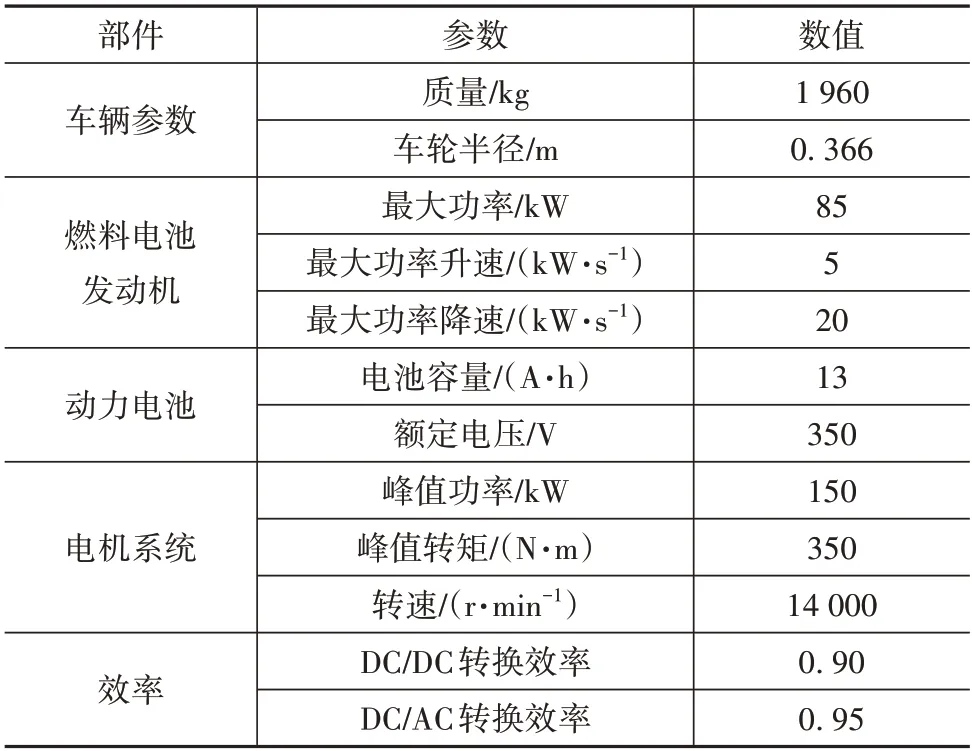
表1 车辆的主要技术参数

为便于分析，将车辆纵向动力学方程简化为

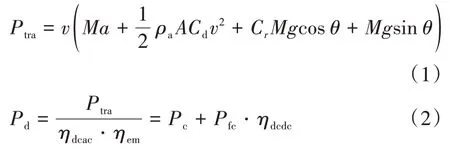
式中：为车速；为加速度；为整车质量；为空气密度；为迎风面积；为空气阻力系数；为滚动阻力系数；为重力加速度；为道路坡度（本文不考虑坡度影响）；、、分别为DC/AC 变换器、DC/DC变换器和电机的效率。

1.2 动力系统凸模型

本文参照文献［11］中的方法对模型进行凸化处理。

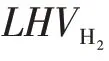
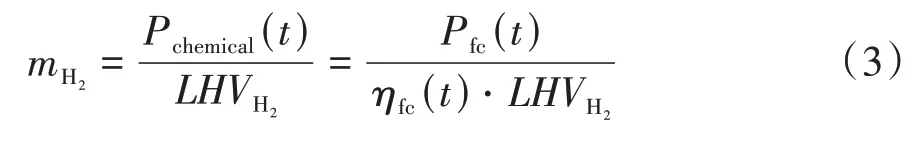
式中为燃料电池发动机的效率，如图3所示，最高效率为60%。

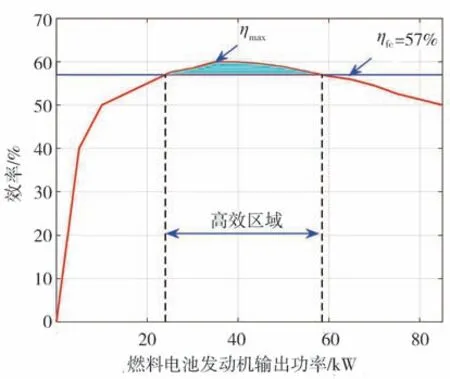
图3 燃料电池发动机效率

根据燃料电池发动机效率，同时保证目标函数的凸性，对化学能进行二次拟合：

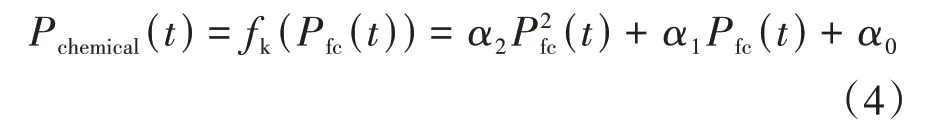
式中、、为拟合系数。

电机系统中的能量转化分为驱动和制动两种过程：

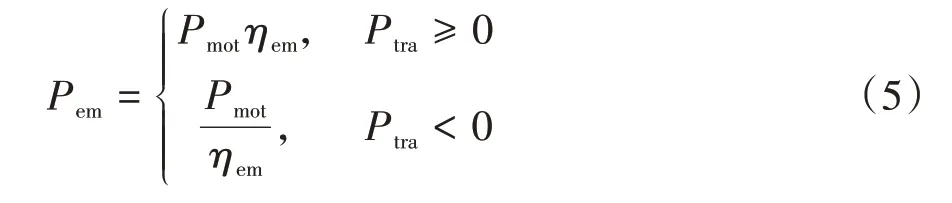
式中为电机系统的效率，如图4所示。

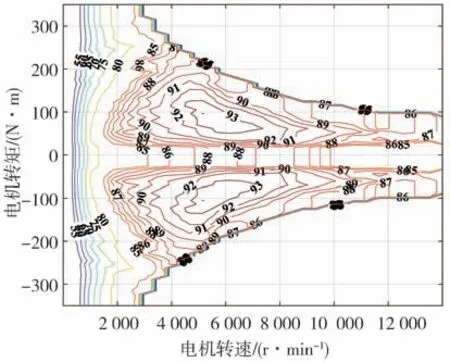
图4 电机系统效率

同理，保证目标函数的凸性，对电机系统的输入和输出功率进行二次拟合：

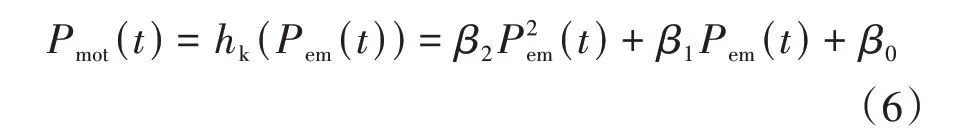
式中、、为拟合系数。

动力电池输出电能会造成荷电状态SOC 的变化，涉及到的参数包括电池电流、容量、开路电压和内阻，具体转化关系如下：

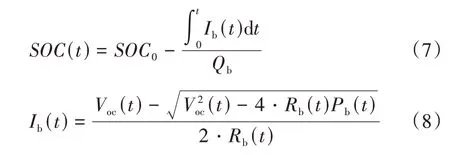
为便于后续引入凸优化方法，本文中将动力电池的开路电压和内阻定义为常数，不随电池SOC 发生变化。所以，动力电池化学能和电能的关系同样可以用二次函数表达：

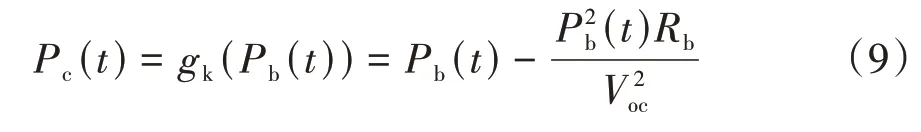
1.3 固定式交通信号配时模型

结合文献［13］，建立固定式交通信号灯配时模型。假设行车路线中每个信号灯的时间节点和运行周期是已知的。定义行驶路线总长度为，信号灯个数为，第个信号灯的位置为s，则

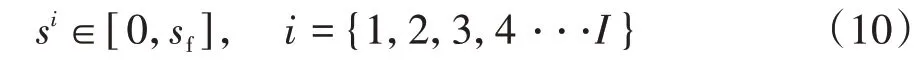
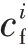
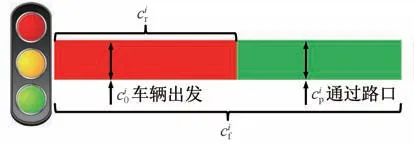
图5 信号灯相位与配时信息

1.4 基于视觉的智能驾驶员模型

基本的智能驾驶员模型（IDM）能够实现车辆加、减速行为的平滑过渡和智能控制，而且能够根据车辆运行的状态推算与前车的期望距离和加速度。

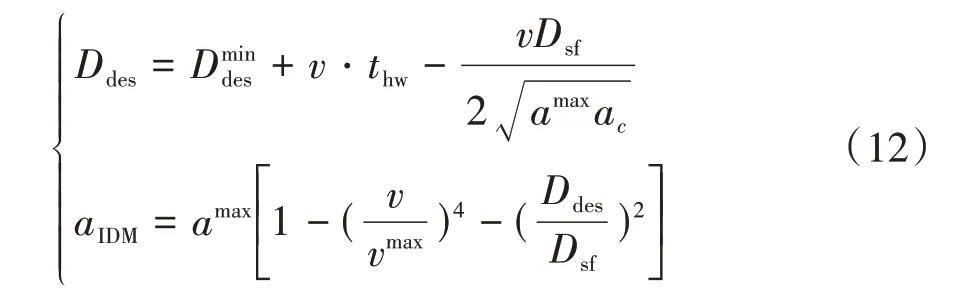
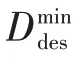
但本文中并无前车，所以引入基于视觉的IDM作为车速规划的基准模型。该模型假设驾驶员能观测到前方距离内信号灯的状态。

2 节能车速规划问题构建

本章介绍通行绿灯窗口的选取方法、基于凸优化的快速车速规划和能量管理方法3部分。

2.1 最优绿灯窗口的选取

根据计算结果绘制燃料电池汽车匀速行驶的静态氢耗图，如图6 所示。可以看出，车辆以5 m/s 的速度匀速行驶时耗氢量最低。主要因为在此速度下，电机系统、动力电池系统和燃料电池发动机的联合效率最高，约为0.414。

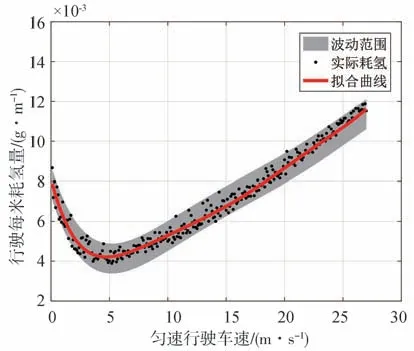
图6 燃料电池汽车静态氢耗图

假设每个绿灯窗口有个候选时刻点，将绿灯窗口均分为+1个时段。基于静态氢耗图，可以计算车辆从当前信号灯的某候选时刻点到下一信号灯某候选时刻点匀速行驶的耗氢量。参照IDM中车辆的抵达时间，借助DP求解车辆通过多信号灯场景的分段匀速行驶氢耗最小的路径，并将其定义为最优匀速行驶路径，最后选取该路径通过的绿灯窗口作为最优绿灯窗口，如图7 所示（图中为3 个信号灯场景，且取1）。

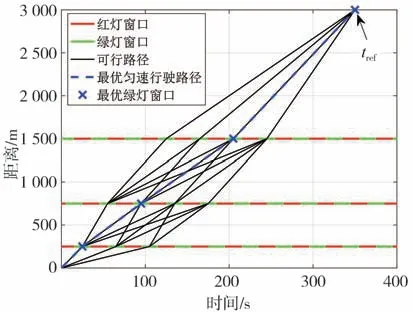
图7 最优绿灯窗口

2.2 车速规划凸问题的构建

在车速规划问题中，以车辆需求功率累计最小为优化目标，建立目标函数如下：

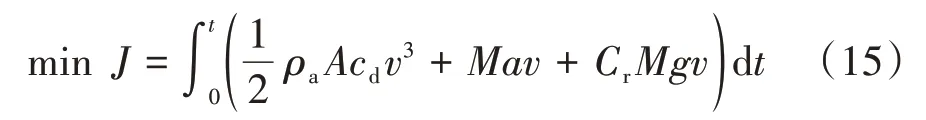
其中，和在时域中的关系可表示为

式中：为初始速度（设置为0）；为元素全为1 的(-1)维列向量；为(-1) ×(-1)的下三角矩阵，且非零元素全为1。

此外，车速规划问题求解时还要考虑信号灯约束，在车辆通行最优绿灯窗口确定的基础上，可将窗口的上下边界作为车辆在该路段行驶路径的约束范围，避免车辆出现闯红灯的现象，如图8所示。

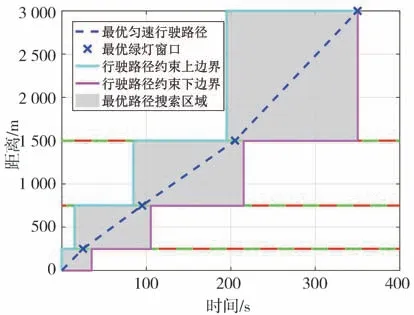
图8 最优路径搜索区域

利用二次规划求解加速度的标准形式为

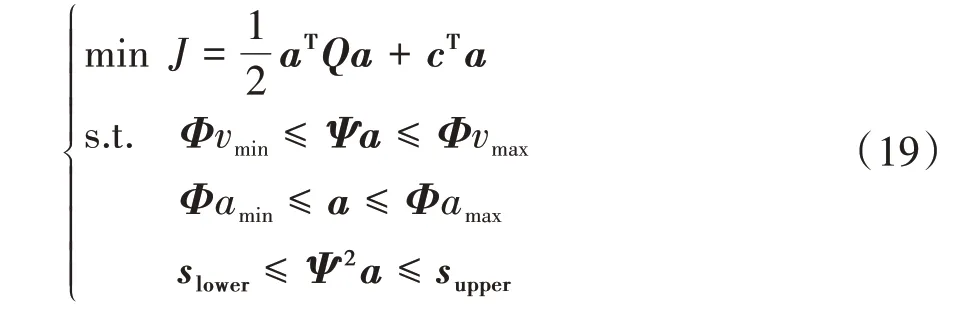
式中：和分别为车辆的最大速度和最小速度；和分别为车辆的最大加速度和减速度；和分别为车辆行驶路径约束上边界和下边界。

2.3 能量管理凸问题的构建

本文参照文献［11］中的方法，以最小氢耗为优化目标，制定燃料电池汽车的最优能量管理策略。结合动力系统结构，燃料电池汽车行驶过程中的总耗氢量可表示为

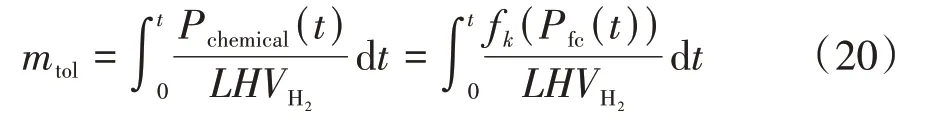
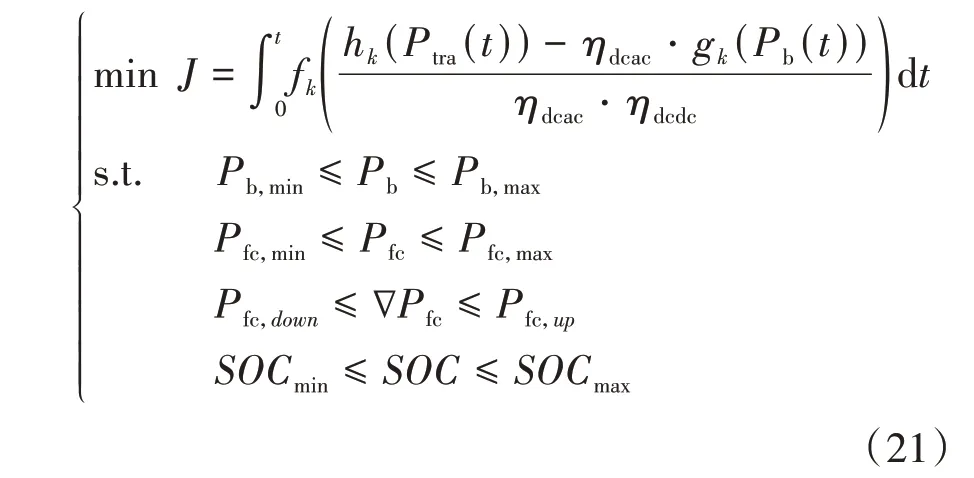
式中：和为动力电池功率的上下界；和为燃料电池发动机输出功率的上下界；和为燃料电池发动机功率变化的上下界；和为动力电池SOC 的上下界。满足ADMM算法的标准形式为

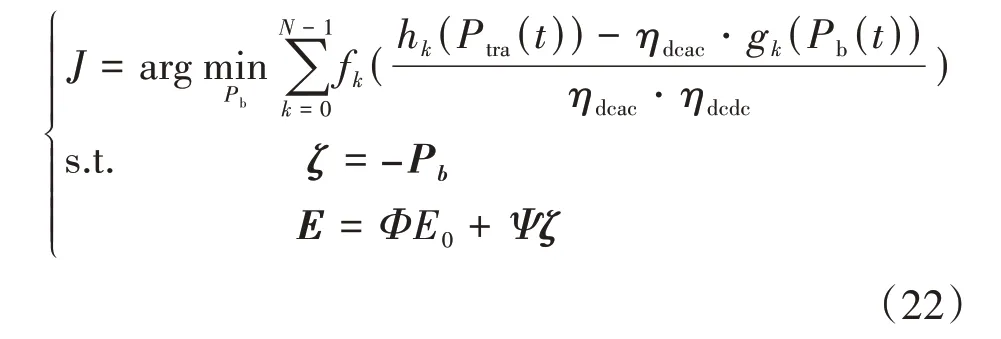
式中：引入作为对偶变量；为动力电池的初始电动势；为动力电池各时刻的电动势。

3 仿真分析

3.1 仿真场景设定

本文仿真路线为一条配备了9 个信号灯、限速60 km/h（16.67 m/s）、总长度2 km 的城市道路。信号灯的位置和相位信息如表2所示。

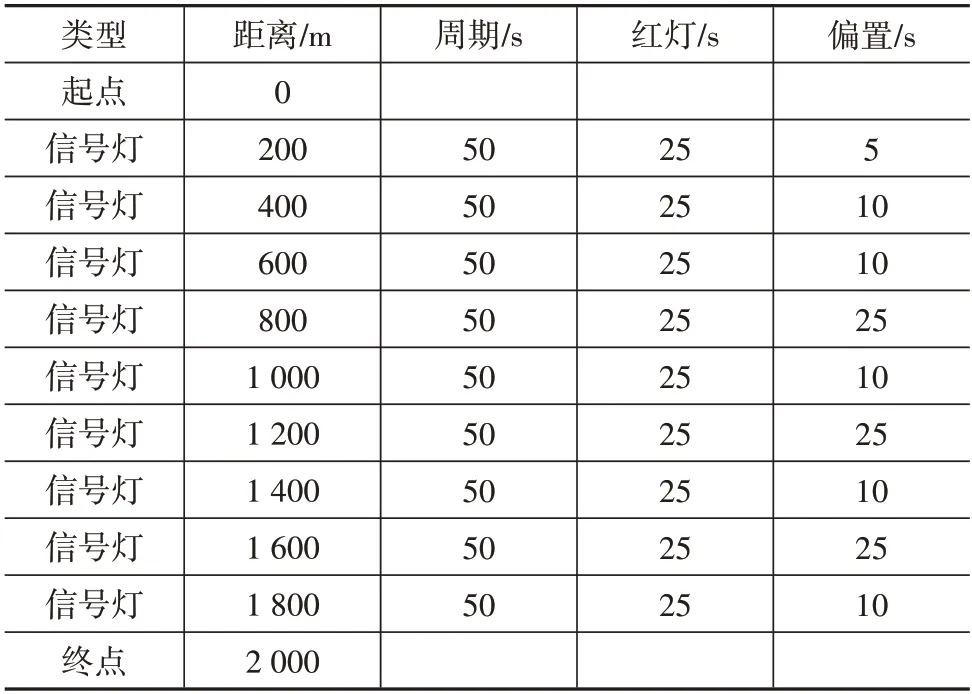
表2 信号灯位置和相位

为满足驾驶舒适性，设置车辆的最大加速度和减速度均为2 m/s。仿真环境为Matlab2016b，CPU Intel i5-8250H，RAM 8GB。

3.2 仿真结果对比分析

在车速规划环节，建立了以车辆需求功率累计最小为优化目标，求解车辆最优加速度的二次规划问题。

仿真时，利用OSQP 对其进行求解，OSQP 是由牛津大学开发的一款基于ADMM 算法求解二次凸优化问题的求解器，计算结果如图9所示（取5）。

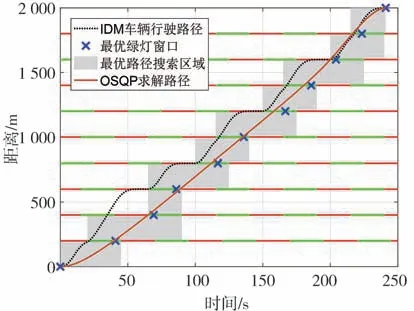
图9 最优行驶路径

从图中可以看出，IDM和OSQP求解的车辆抵达时间保持一致，均为241 s。灰色区域为OSQP 求解最优行驶路径的搜索区域，即车辆位置在不同时刻的可行域，如图显示，最优行驶路径满足该约束范围，证明结果是可行的。从两种方法的通行绿灯窗口选择来看，除第2 个信号灯绿灯窗口选择不同外，其余均保持一致。在IDM 中，行驶路径轨迹波动较大，出现了4 次等待红灯的情况。相对而言，OSQP求解的最优行驶路径更显平滑，与DP求得的最优匀速行驶路径较为接近，并且行驶过程中没有出现等红灯的情况。

从图10 中可以看出，两种方法的速度和加速度变化均未超出限制范围，且起点和终点时的速度均为0。但总体而言，IDM的速度和加速度变化较为剧烈，OSQP的速度和加速度只有在起点和终点附近变化较大，中间过程则较为平顺。

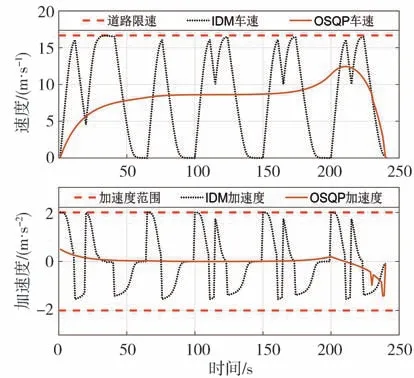
图10 速度和加速度

图11 为两种方法的车辆需求功率累计值和电机效率的对比。IDM 的车辆需求功率要远远高于OSQP，而且电机运行在高效区域的频次也低于OSQP，表3 中给出了详细数据。由表可知，OSQP 的总需求功率比IDM 低48.9%，且电机工作点的平均效率比IDM要高10.1%。

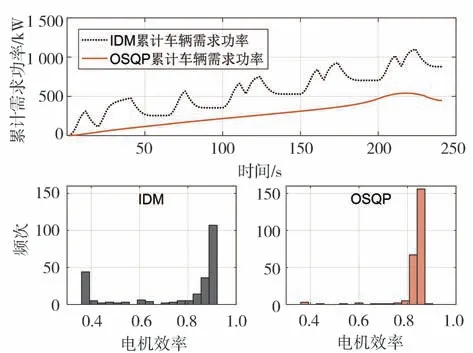
图11 累计车辆需求功率和效率

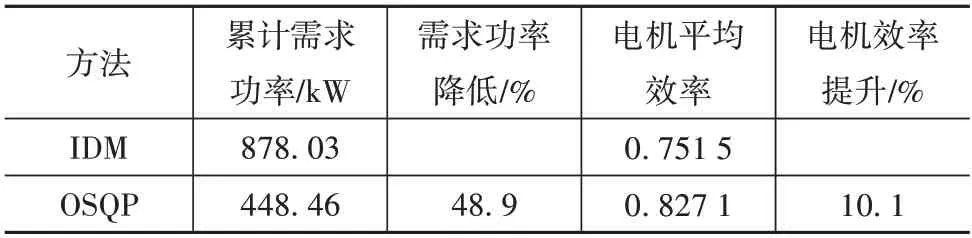
表3 车速规划仿真结果对比

同样，在能量管理环节，建立了以最小氢耗为优化目标且满足ADMM 的标准范式。本文中还运用DP求解了该能量管理问题，以验证ADMM 算法的优越性。仿真时，通过调试参数保证动力电池电量不变，结果如图12 所示。根据车速规划和能量管理的方法不同，将仿真分为“IDM+ADMM”、“IDM+DP”、“OSQP+ADMM”和“OSQP+DP”4 种情况。其中，“OSQP+ADMM”为本文所提出分层凸优化的方法，在上层中利用OSQP 求解车速规划的凸二次规划问题，在下层中利用凸优化中的ADMM 算法制定车辆的能量管理策略。从图中可以看出，与IDM 相比，OSQP 方法的动力电池SOC 波动较小，耗氢量较低，且燃料电池发动机平均效率也较高。

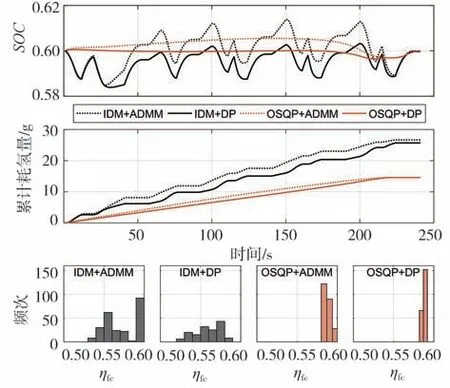
图12 能量管理仿真结果

表4展示了4种方法的计算时间和氢耗，可以看出，虽然“IDM+ADMM”的计算速度最快，但氢耗也最高，主要原因是基于视觉的IDM 仅仅是模拟真人驾驶，驾驶员只能在视觉范围内根据当前信号灯的状态做出加速或制动的行为，并没有基于全局考虑，所以该方法生成的车辆行驶路径缺乏最优性能。而且从“IDM+DP”的结果可以看出，在IDM 行驶路径下，即使运用基于DP 的能量管理策略也难以达到OSQP计算的最优路径的节能效果。

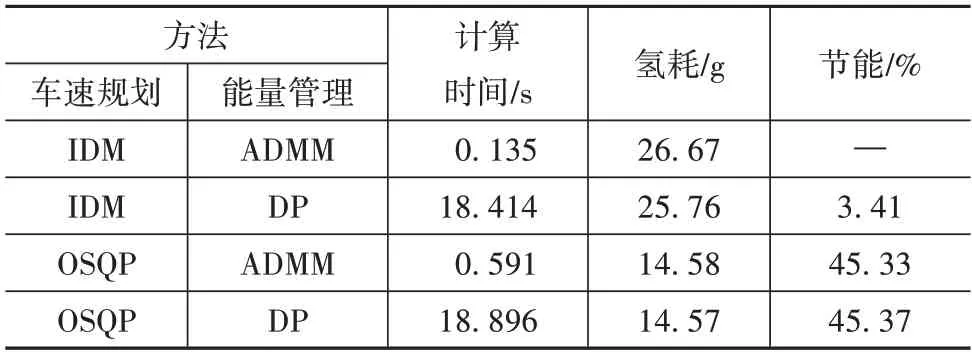
表4 不同方法的仿真结果对比

与“IDM+ADMM”相比，“OSQP+ADMM”虽然多花费0.4 s 的计算时间，但行驶过程节约了45.33%的氢耗。由此说明，基于相同的能量管理策略，OSQP 求解的最优行驶路径比IDM 的节能性高40%以上。当然，同样的情况还出现在“IDM+DP”和“OSQP+DP”对比中。

此外，分别对比前两种方法和后两种方法可知，当车速规划方法相同时，基于ADMM 的能量管理策略与DP 离线求解的最优结果相近，而且计算效率更高。

4 结论

本文中提出一种基于分层凸优化的燃料电池汽车快速车速规划和能量管理方法。基于静态氢耗图，利用DP 求解车辆通行的最优绿灯窗口，并以此确定最优行驶路径的搜索区域。建立以车辆需求功率累计最小为优化目标的二次规划问题，运用OSQP求解最优行驶路径。最后，建立以最小氢耗为优化目标的能量管理问题，并利用ADMM 进行求解。结果表明：（1）本文中提出的方法比IDM模型中电机工作点的平均效率高10%；（2）基于ADMM 能量管理策略验证，本文所提出的方法比IDM 模型的氢耗低45%，且与DP 离线计算的氢耗仅差0.02%；（3）在能耗相近的同时，本文方法能够在1 s内完成多个信号灯的车速规划，具备实时优化的潜力。