基于分段优化的车辆换道避障轨迹规划*

唐 斌，许占祥，江浩斌，蔡英凤，胡子添，杨铮奕

（1.江苏大学汽车工程研究院，镇江 212013；2.江苏大学汽车与交通工程学院，镇江 212013）

前言

换道避障作为智能驾驶的基本功能，对提高车辆的行驶安全性、通行效率和智能化水平具有重要作用。换道避障轨迹规划是连接智能车辆感知决策与跟踪控制的重要环节，如何有效地规划一条能够确保车辆平稳、舒适和安全地完成避障的轨迹，成为当前智能驾驶领域的研究热点。

车辆轨迹是一条带有时间戳的路径曲线，当前对车辆的轨迹规划方法研究大致分为以下4 类：基于搜索的规划方法、人工势场法、基于随机采样的规划方法和基于离散优化的规划方法等。基于搜索的规划方法是通过状态格子将道路空间离散化，然后通过搜索算法来搜索最优轨迹，常见的搜索算法有Dijkstr、A*、D*。A*通过启发式函数使靠近目标的节点优先扩展，但状态格子较多时存在效率较低的问题。Aine 等在A*的基础上提出了MHA*算法，引入多个启发式函数协调路径代价，可以兼顾路径的最优性与搜索效率，但规划路径并不能满足车辆运动学约束。人工势场法由Khatib 提出，算法简单效率高，但容易陷入局部最优，且未考虑车辆的运动学约束，规划出的路径存在不可行的概率。安林芳等提出了一种新的障碍点构建方式以防止目标不可达和陷入局部最优的缺点。Rasekhipour 等将人工势场法与最优控制相结合进行路径规划，可保证路径的可行性和最优性。但人工势场法对复杂场景的势场构建难度较大。基于随机采样的规划方法有快速随机搜索树（rapidlyexploring random tree，RRT）和概率路图法（probabilistic road map，PRM），该类算法采样搜索能力强，但由于采样盲目性较大，浪费过多的计算资源，且由于采样点是随机的，导致路径不够平滑。基于离散优化的规划方法是目前应用最为广泛的，该方法是对结构化的道路进行有序采样，避免了随机采样的盲目性，可以大大减少计算难度，但对于复杂场景的适应能力仍有待探索。郭蓬等针对结构化道路，有序地进行采样生成多条路径，提出一种考虑到车道线曲率和障碍物模型信息的代价函数，通过代价函数进行优化选取局部路径。邓海鹏等在车辆恒速行驶时通过MPC（model predictive control）对车辆紧急避障路径进行优化处理，但并未对车辆速度进行规划。

针对上述算法存在的问题，为进一步提高算法的实时性和最优性，对道路空间进行规则采样以减少计算资源的浪费，通过单次遍历轨迹簇优选出一条参考轨迹以提升车辆的行驶平顺性，且将后续轨迹优化由非凸空间转变为凸空间，通过分段曲线对参考轨迹进行实时优化求解得出最优的避障轨迹以提高避障安全性和效率。为此基于分层式架构对换道避障轨迹规划进行研究，首先将轨迹降维分解成-曲线和-曲线，根据本车当前状态基于五次多项式拟合候选轨迹簇；考虑到路径的平滑性、行驶平顺性、行驶效率以及碰撞风险等因素设计评价函数，选取出最优的一对曲线的组合作为参考轨迹；以参考轨迹为引导构建优化目标函数，基于分段样条曲线对-曲线和-曲线进行优化求解，通过外点法求解得出最优轨迹。该方法更加类似人类的驾驶员思考过程，在参考轨迹的引导下会保证轨迹的平顺性且避免轨迹的优化陷入局部最优，大大减少非线性规划目标函数的复杂度，因此降低了轨迹规划对处理芯片的算力要求，且提高轨迹的避障调整能力与舒适性，为自动驾驶换道的工程实践提供一种有效的解决方案。

1 确定候选轨迹

针对换道避障轨迹规划研究，定义如图1 所示的换道场景。图中，假定当前车辆所处直道行驶，本车道中心线cl和目标车道中心线cl上对应存在障碍车辆V和V，bound与bound分别为道路的上下边界，div为车道分界线，本车车辆记为Auto。

当本车接收上层换道指令时，此时刻作为换道周期的起始时刻，以该时刻车辆质心在cl上的投影点作为坐标原点，以cl作为轴，过原点做轴的垂线作为轴，建立如图1 所示的换道坐标系。图中与分别为车辆在换道起始时刻在坐标系上的横向位置和航向角。设定换道初始时刻，本车以=0、=20 m/s、=0 行 驶，车 辆V在(-20 m，3.5 m)的位置以30 m/s 的速度行驶，本车道车辆V在(30 m，0)的位置以车速15 m/s行驶。

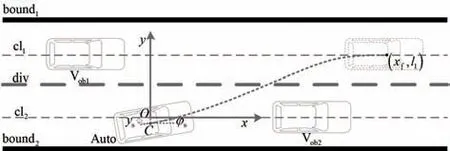
图1 换道场景示意图

1.1 候选轨迹生成

驾驶员在进行换道时，期望车辆会最终行驶在目标车道中心线上，且车辆完成一个换道周期一般所行驶纵向位移20 m ≤≤200 m 和所需时间4 s ≤≤9 s；分别对与采取和个采样点，记为x和t，这里为减少计算量，且确保参考轨迹的可靠性，纵向位移每间隔10 m 取一个采样点，所需时间每间隔1 s取一个采样点。

车辆轨迹规划是规划出车辆的横向位置、纵向位置和行驶时间之间的复杂三维问题。为简化问题难度，将轨迹转化成车辆横向位置随纵向位置变化的-曲线和车辆纵向位置随行驶时间变化的-曲线两个二维问题。为保证各曲线的平滑性，且由于各曲线的起始点和终止点存在3 个约束等式，故使用五次多项式拟合各候选轨迹。根据上述离散采样点x和t，通过五次多项式分别拟合候选-曲线y= f()和候选-曲线x= g()计算如下：

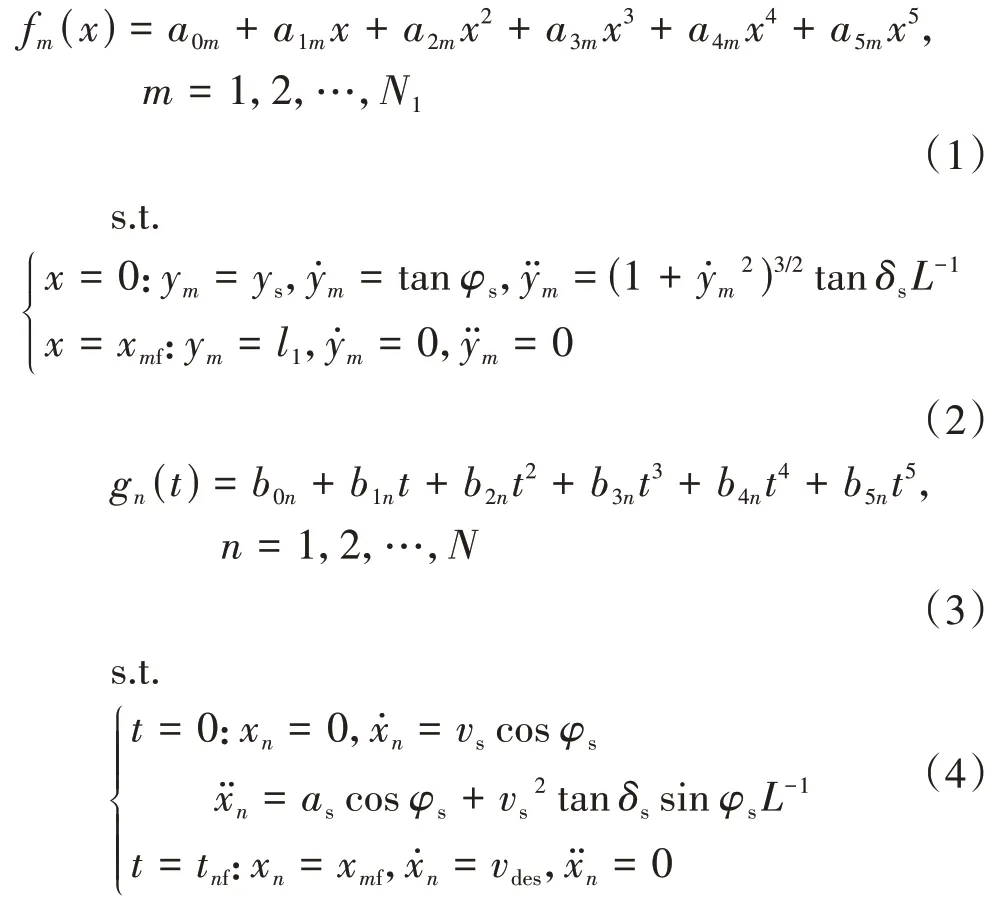
式中：，，...，为第条-曲线系数；、和分别为起始时刻车辆车速、前轮转角和加速度；为车辆轴距；为cl对应的横向坐标值；，，...，为第条-曲线系数；表示车辆完成换道后的期望车速，考虑到换道的舒适性，这里的取值是根据本车的初始车速与换道完成时间所确定；=×。

1.2 候选轨迹筛选

为确保候选轨迹的可行性并减少后续轨迹评价的计算量，将满足车辆行驶条件的轨迹保留作为下一阶段的候选轨迹，反之则被剔除；车辆的行驶条件包括道路边界约束、车速约束、加速度约束、转弯半径约束和路面附着力约束，即

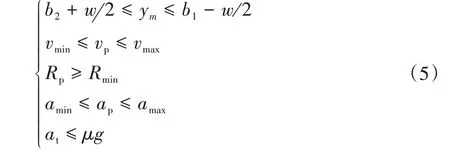
式中：为车宽；与分别为bound和bound对应的横向坐标值；、、、与分别为道路允许最低车速、最高车速、本车的最小转弯半径、最小纵向加速度和最大纵向加速度；为路面附着系数；为重力加速度；y、、、与分别为候选轨迹的横向位置、车速、转弯半径、车辆纵向加速度和总加速度；这里设定该道路所允许的车速范围为0～35 m/s，在该路上行驶的车辆为-6 m/s，为4 m/s，为2.6 m，最大值为35。符合车辆行驶条件的候选轨迹如图2所示。

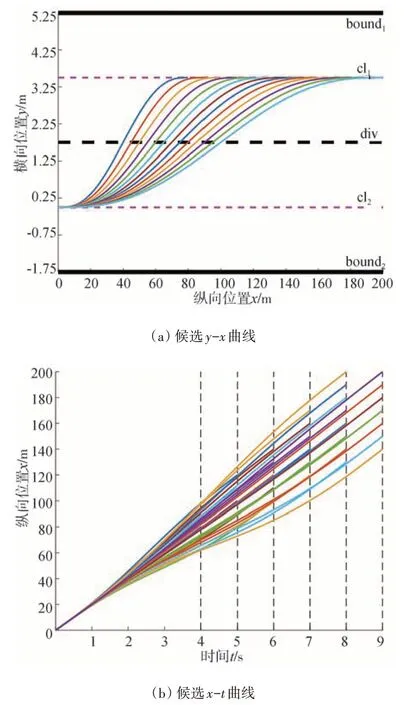
图2 候选轨迹图

2 选取参考轨迹

考虑到各候选参考轨迹的舒适性、碰撞风险性和利他性等因素，需要对这些候选轨迹进一步评价以选取出最优参考轨迹，为车辆当前时刻的换道避障提供方向以及速度的参考值。

2.1 评价函数建立

构建评价函数见式（6），选出值最小的轨迹作为最优换道参考轨迹。评价函数的建立主要包括参考-曲线评价函数、参考-曲线评价函数和障碍风险评价函数。

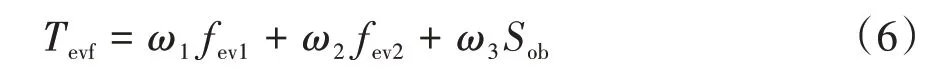
式中、和分别为、和的影响系数。根据式（7）、式（8）和式（11）计算可得：取值范围为0～4.3；的取值范围为0～5.5；的取值范围为1～3；本文在轨迹选取时，综合舒适性和安全性等指标最终取=1.2、=1、=1.3 以获取最优参考轨迹。、和函数的构建具体内容如下：

（1）参考-曲线评价函数，为保证参考-曲线的平滑性、行驶效率，要求参考-曲线的弧长、曲率和曲率的变化率要尽量较小。为方便计算分别对上述指标进行简化处理，构建表达式为

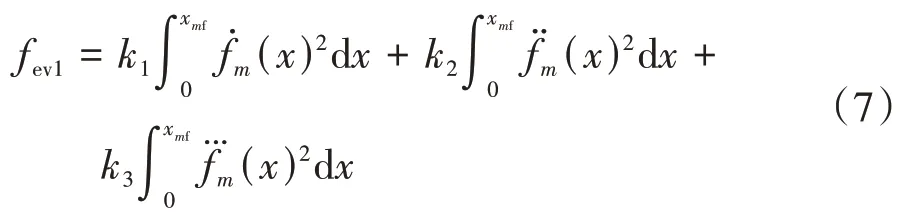
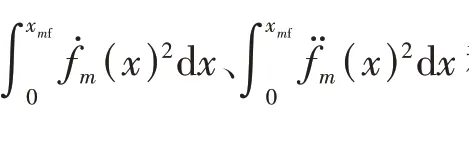
（2）参考-曲线评价函数，为保证参考-曲线的利他性和舒适性，要求参考速度应与该车道的期望车速的差值、参考加速度和参考加加速度尽量较小。经过简化处理后，构建的表达式为

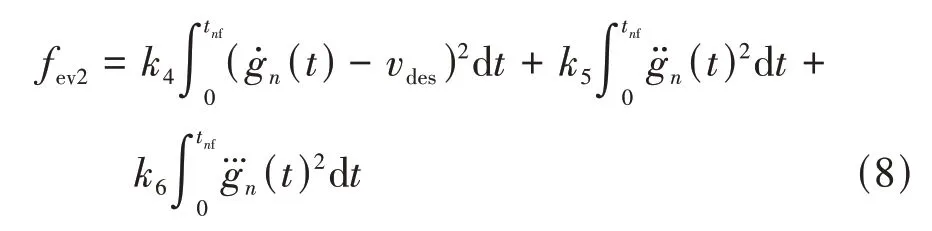
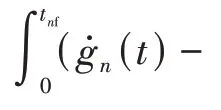
（3）障碍风险评价函数，为保证本车与其他车辆的安全性，在换道避障过程中应让本车与障碍之间的风险距离尽可能大以减小碰撞风险。考虑到目标车道障碍车辆与本车道障碍车辆对于本车影响不同，将又分为本车与本车道障碍物之间的风险距离和本车与目标车道障碍物的风险距离，如图3 所示。表示当车辆行驶到车道分界线上时与目标车道障碍物之间的风险距离，计算公式如式（9）；表示车辆在参考轨迹上行驶与本车道障碍物的最小风险距离，计算公式如式（10）。

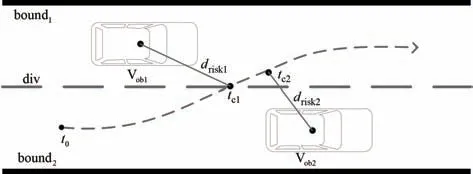
图3 风险距离示意图

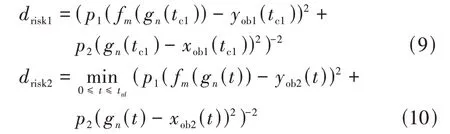
式中：与分别为横向距离影响系数和纵向距离影响系数，其取值可根据高速场景下障碍风险影响范围来确定，本文中以纵向距离为20 m、横向距离为3.5 m 构造风险距离等势面，则可得=0.08，=0.0025；()、()分别表示车辆V横向位置和纵向位置随时间的变化关系；()、()分别为车辆V在时刻的横向位置和纵向位置；为候选轨迹在本车道与目标车道分界线上所对应的时刻。

为保证车辆的安全性，当轨迹点距离障碍车辆较近时，风险值应快速增长，为此利用指数函数的增减特性对风险函数进行设计，根据障碍车辆的风险距离，构建障碍车辆风险评价函数如式（11），得出障碍车辆风险示意图如图4 所示。需要指出，本文设定本车外围尺寸长为4.3 m，宽为1.8 m，当本车与障碍车辆距离较近时碰撞风险值达到一定值则说明碰撞风险较大，即当≥或≥时，结合图像可以看出，当风险值达到3 以上时，便与障碍有发生碰撞的风险，此时该候选轨迹不应被选取作为车辆的参考轨迹，因此本文取=3，若车辆外围尺寸更大，则的取值应更小，使避障时的碰撞风险较小，反之可以适当增加的取值。

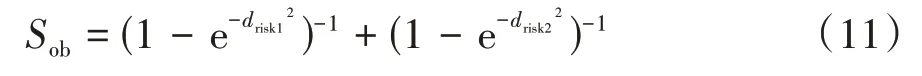
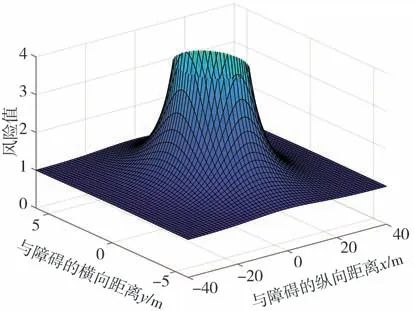
图4 障碍车辆风险示意图

2.2 参考轨迹选取与分析

通过2.1 节中所建立的轨迹评价函数，求出各候选参考轨迹的值，选取值最小的轨迹作为换道参考轨迹。记参考-曲线为=()，记参考-曲线为=()。对图3中候选轨迹进行选取，结果如图5所示。

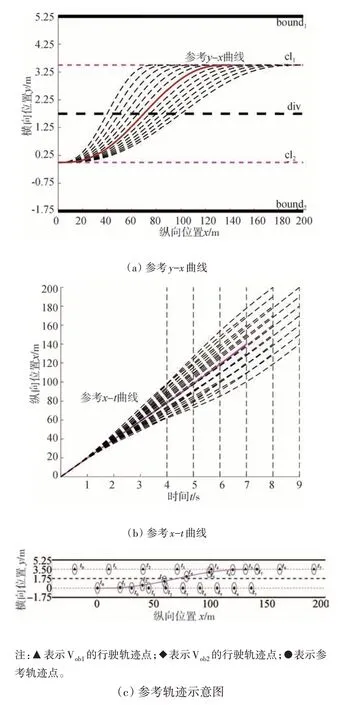
图5 参考轨迹

将=()与=()组合起来得到最优参考轨迹示意图，如图5（c）所示，图中椭圆表示车辆在轨迹点上的粗略几何形状，，，...，表示各个时刻车辆所在的位置坐标。由图5（b）可以看出，参考轨迹在0～3 s时段之间，曲线斜率几乎不变，说明参考轨迹先保持当前车速，结合图5（c），此时可以看到规划轨迹在保持与本车道障碍车辆一定的安全距离的同时，维持当前车速等待目标车道的车辆先行，时刻后参考-曲线斜率稍有增加，为使车辆行驶到左侧快车道不影响其他车辆的行驶，这样不仅减少了与障碍车辆的碰撞风险且使本车的行驶也更加平顺。

本文仅定性地分析了参考轨迹的选取是否合理，因为参考轨迹并不作为车辆最终跟踪的轨迹，仅为整个换道避障过程提供引导。由于存在参考轨迹的引导，可以确定优化空间，将原本非凸空间转变成凸空间，且可以大大简化目标函数的建立。

3 轨迹优化修正

车辆在行驶过程中，障碍物的运动状态是实时变化的，为保证车辆行驶的安全性，车辆实际行驶轨迹也必须根据障碍物的运动状态进行实时修正。因此，根据障碍物实时的状态信息包括障碍物的位置和速度，通过分段五次多项式曲线对参考轨迹进行实时优化修正得出最优换道轨迹。

3.1 构建分段多项式曲线

分别构建段-曲线y= f()和-曲线x=g()，如式（12）和式（13）；这里取值较大时会增加优化算法的计算负担，而取值较小时又会造成避障轨迹优化效果不佳；为综合考虑计算的实时性与避障轨迹的效果，经多次测试最终取=10。

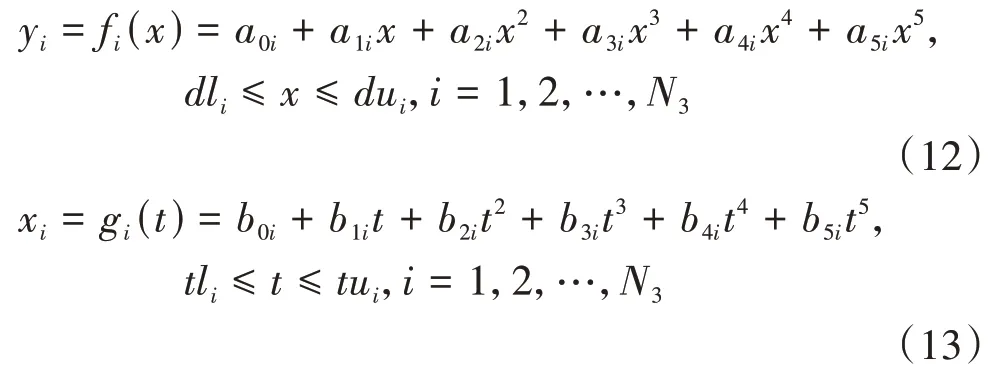
式中：，…，与，…，分别为y= f()和x=g()各项系数；dl与du分别为y= f()自变量取值的下限和上限；tl与tu分别为x= g()自变量的下限和上限；dl= g(tl)，du= g(tu)。

3.2 优化目标函数

优化目标函数使优化轨迹能够远离障碍的同时又会按照参考轨迹的引导去行驶以保证安全性和舒适性。因此，构建-曲线优化目标函数如式（14），包括参考线引导函数Gp和障碍物排斥函数Rp，其中Gp表征分段曲线与参考路径的贴合程度，Rp表征各分段样条曲线连接点与障碍物的排斥程度，这里取值越小，说明优化效果越好。同理，构建-曲线优化目标函数如式（17），Rp、Rs的构建与2.1 节中的障碍车辆风险评价函数的原理类似，不做过多介绍。

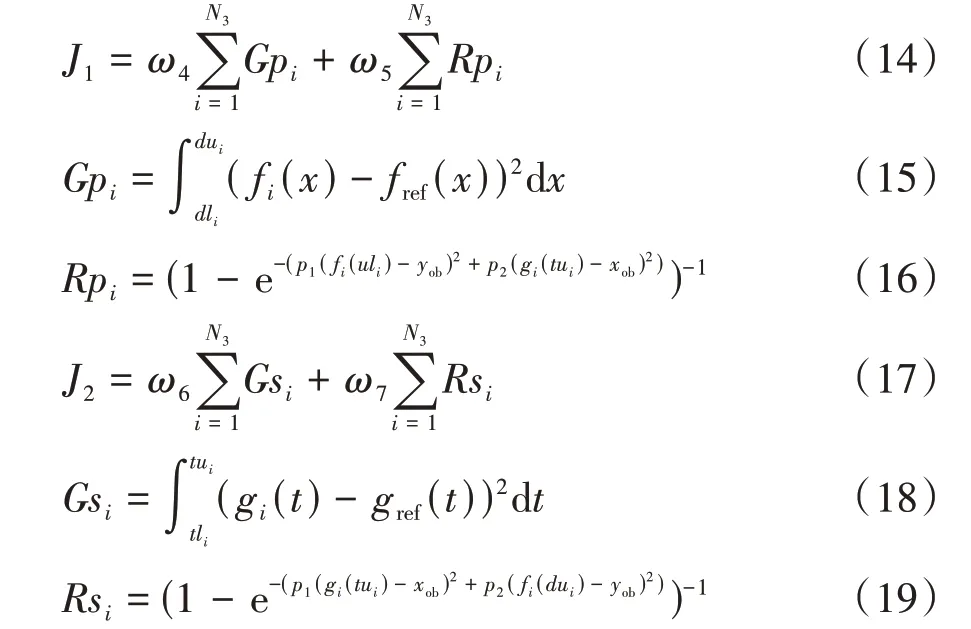
式中：、、、分别为Gp、Rp、Gs、Rs影响系数；为障碍物纵向位置；为障碍物横向位置；与这一对参数组合选取时需要相互协调，如图6 所示。当相对取值较大时，优化后的-曲线与参考-曲线贴合程度较好，而远离障碍物的趋势有所减小。最终取=1、=4 较为合理；同理，对-曲线进行优化时，取=1、=6较为合理。

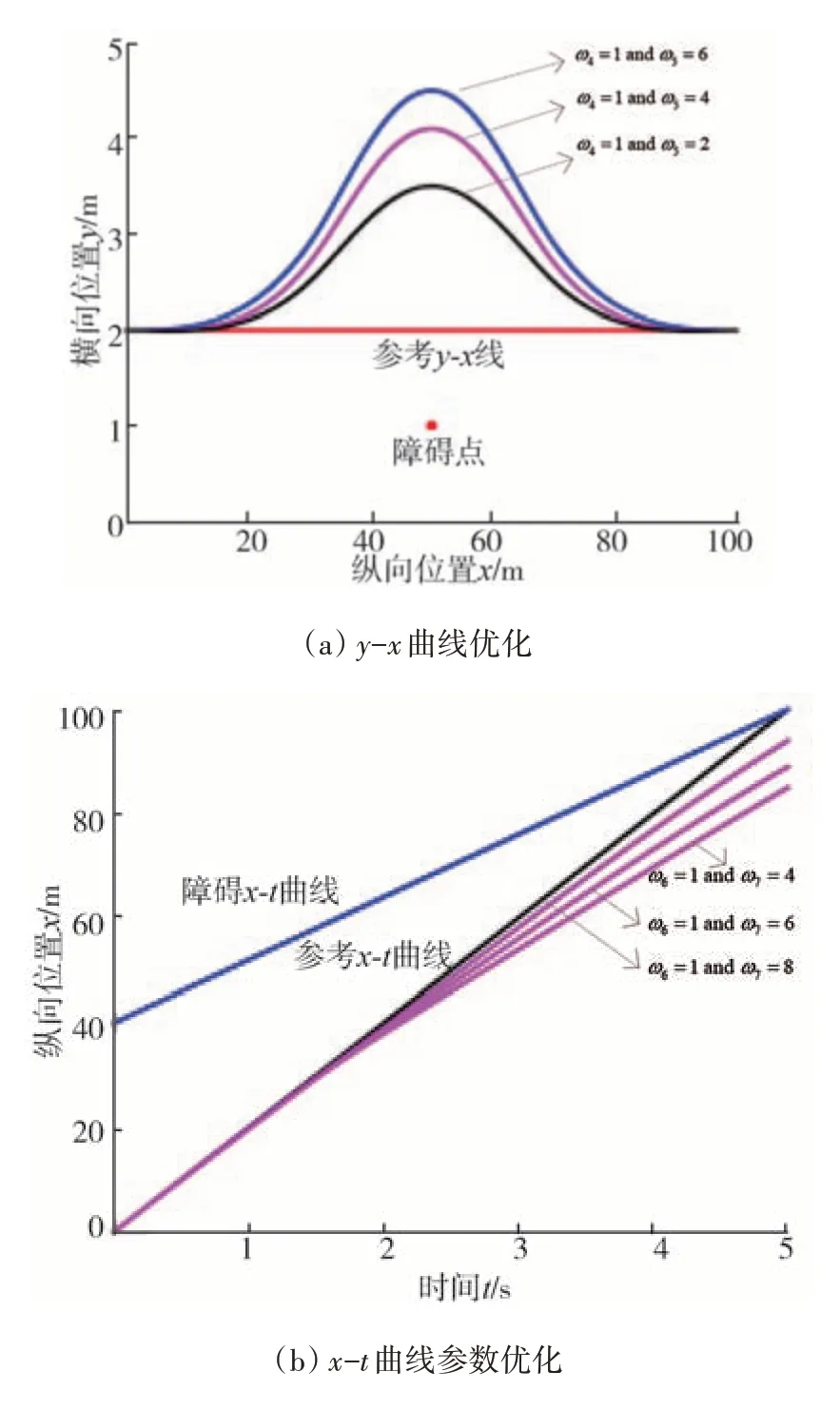
图6 优化参数图

3.3 轨迹约束条件

为使优化求解出的最优轨迹始终是可行的，必须对分段多项式曲线加以约束来满足车辆的行驶条件。-曲线约束包括道路边界约束、最小安全车距约束、最小转弯半径约束和侧向加速度约束，如式（20）。-曲线约束包括最小安全车距约束、路面附着约束、车速约束和车辆加速度约束，如式（21）。取=0.5，=0.8。

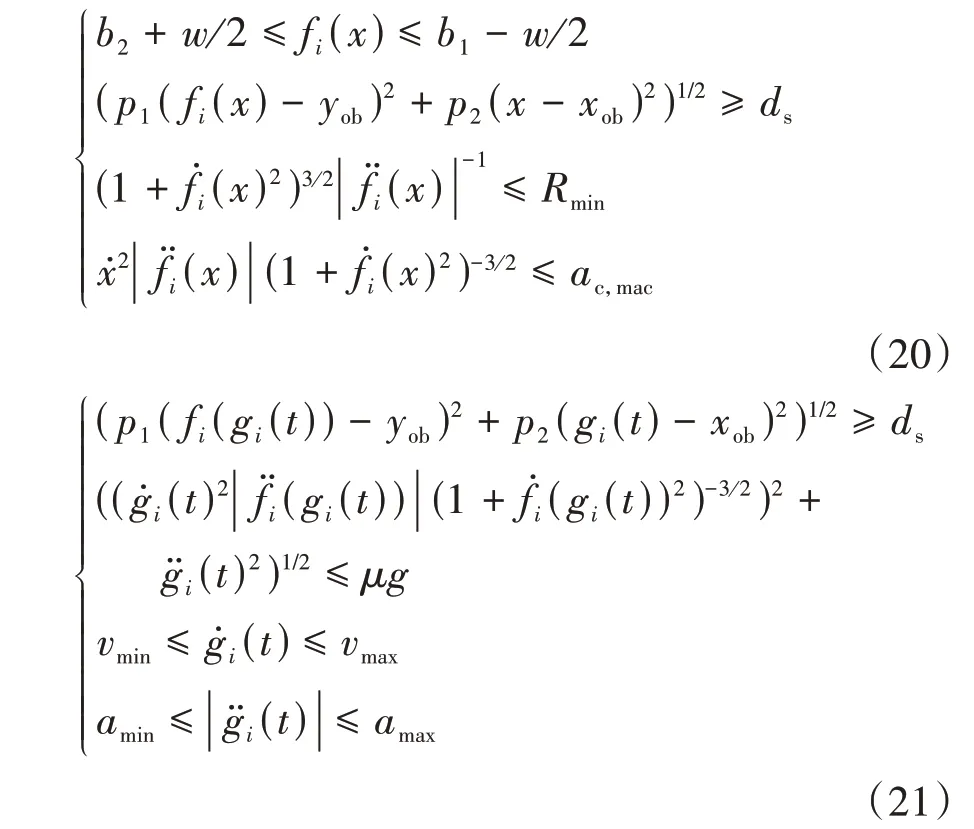
以当前车辆状态为优化初始约束条件如式（2）中=0 时和式（4）中=0 时对应的等式约束，轨迹优化的末端约束与参考轨迹不同，为使轨迹优化效果更好，优化修正能力更强，对优化轨迹的末端位置不加以固定约束，只需满足以下条件即可：

同时，根据车辆的运动学特性，相邻两段多项式曲线必须保证平滑连接，平滑连接条件为

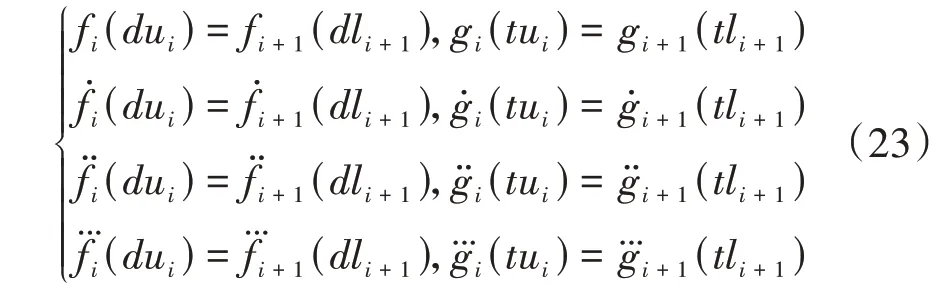
3.4 轨迹优化求解

前述的准备条件完成后，也就将轨迹优化问题转换成带约束的非线性规划求解问题。下一步对轨迹进行实时优化求解，每个采样时刻分别对-曲线和-曲线进行更新一次以满足障碍车辆运动状态实时变化的要求，优化流程见表1。表中，为车辆换道起始时刻，为采样周期，为换道结束时刻，()和()分别为优化后的车辆行驶轨迹。

表1 轨迹优化流程

对于带约束的非线性规划问题简记为式（24）和式（25）的形式，通过罚函数法（外点法）对目标函数与在约束条件下取得最小值时，求解出向量和。向量和分别代表分段-曲线系数，…，和分段-曲线的系数，…，。

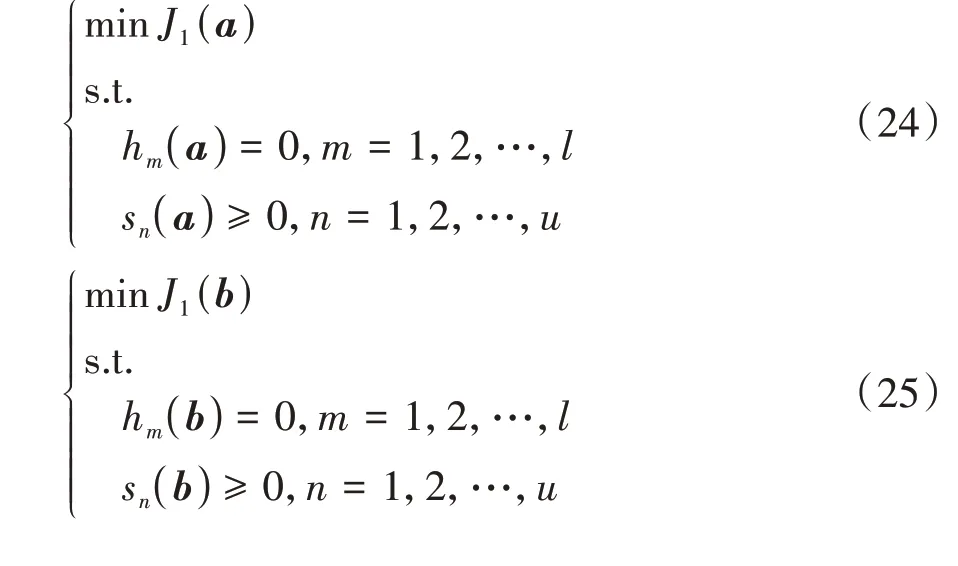
4 结果分析

4.1 场景设定

当上层决策车辆执行换道避障指令时，如车辆状态如第1 节中所述，随后障碍车辆行驶状态发生变化，按照以下A、B 两种情况行驶，通过仿真分析，以验证算法的可行性。

A.车辆V与V按照换道初始时刻的运动状态匀速行驶；

B.车辆V以加速度-1 m/s减速行驶，车辆V以加速度-1 m/s减速至28 m/s，再以加速度0.4 m/s加速至30 m/s。

4.2 仿真结果

应用MATLAB 对文中所设计的算法进行编程，优化采样周期，取为0.1 s。当障碍物的行驶状态按4.1 节中所述的A、B 两种场景变化时，得出优化轨迹分别如图7和图8所示。

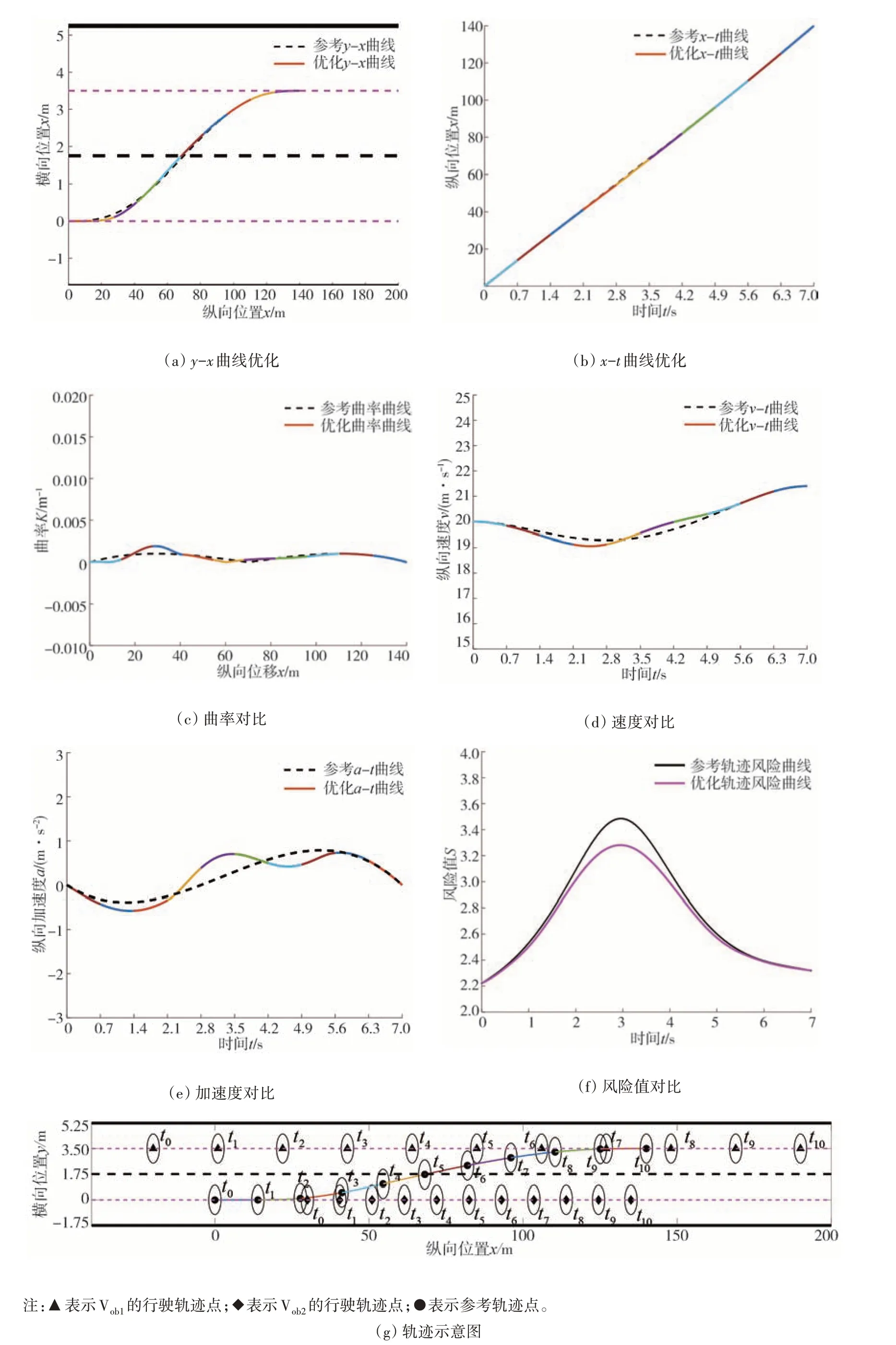
图7 A场景下优化结果

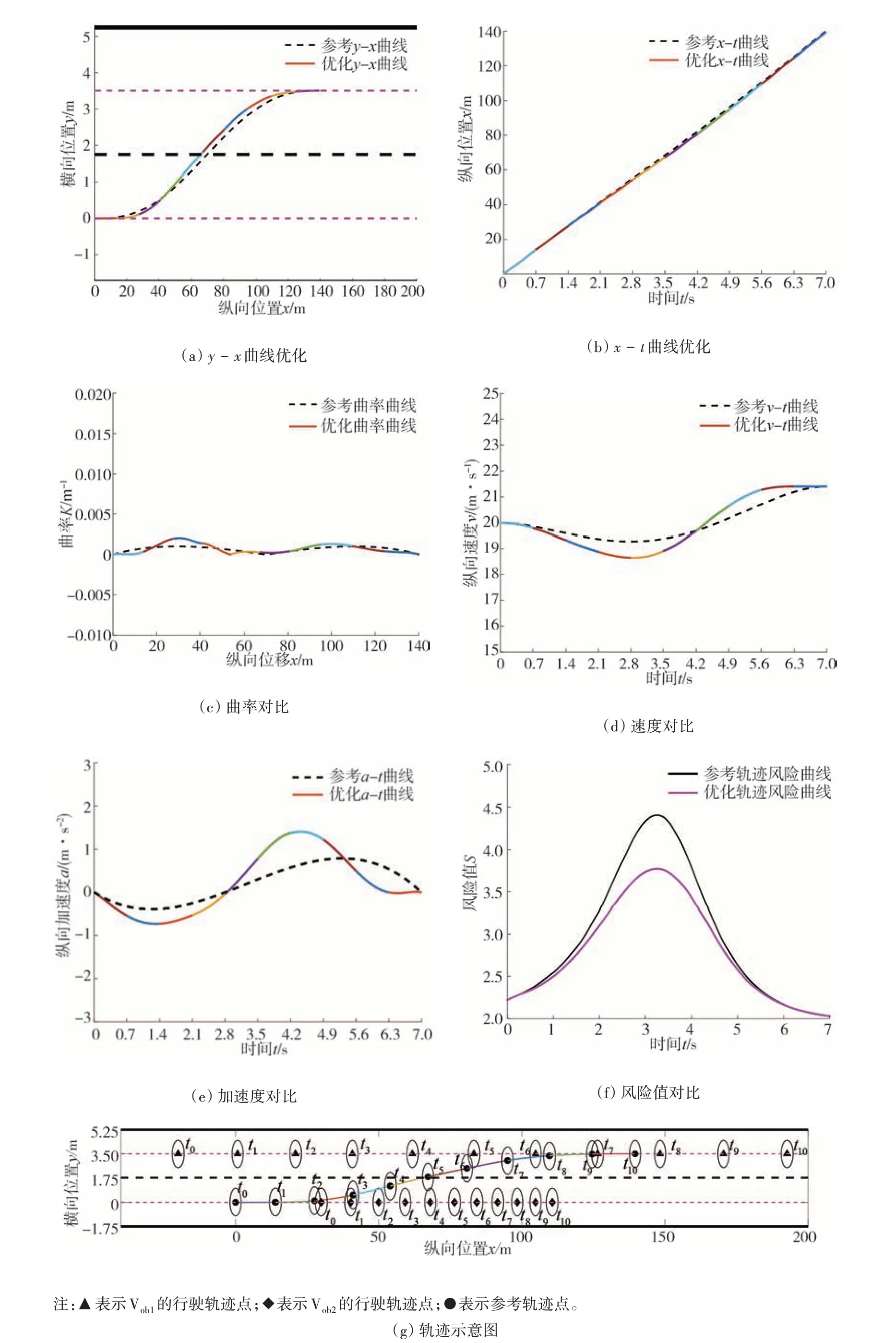
图8 B场景下优化结果

考虑到轨迹的最优性，本车最终所跟踪行驶的轨迹会随障碍车辆的运动变化进行实时的优化调整，从图5（c）中可以看出本车优化后的轨迹会随换道参考轨迹引导换入目标车道障碍车辆V的后方，从而避免优化求解陷入其他非最优的局部空间。

当障碍车辆按A 场景运动时，结合图7（a）和图7（b）可以看出，优化后轨迹相比于换道参考轨迹做了微弱调整，主要调整发生在纵向位置20～80 m 之间，相比于参考-曲线横向调整范围约在±0.1 m之间，相比于参考-曲线纵向调整范围0～0.5 m 以内；同时由图7（c）可以看出，优化后的-曲线的曲率范围在0～2.5 × 10m之间，曲率相对较小说明优化后的-曲线平滑性没有受到太大影响，由曲率和车速可计算得到车辆的侧向加速度不超过1.3 m/s，可以满足车辆行驶的侧向稳定性要求；由图7（d）和图7（e）可以看出，优化后的纵向车速和纵向加速度所在的范围分别为19～22 m/s 和-0.6～0.8 m/s，均可以确保车辆平顺、稳定地行驶；由图7（f）可以看出，优化后的轨迹相比于参考轨迹的风险值有所下降，下降范围在0～0.4。综上可以看出，优化后的轨迹避障灵活度更高，相比参考轨迹舒适度略有下降，但避障风险更低，安全性大大提高。结合图7（g）可以看出，车辆在换道开始阶段先进行轻微减速，以保证与本车到障碍车辆的跟车距离，同时由于目标车道障碍车辆的临近，优化后的-曲线也进行微弱的下调以更小地影响它车的行驶；待到时刻后，车辆所受到的碰撞风险较小，这时车辆开始逐渐加速以跟随参考轨迹的引导换入目标车道。

当障碍车辆按B场景运动时，结合图8（a）和图8（b）可以看出，优化后轨迹相比于换道参考轨迹做了较大调整，主要调整发生在纵向位置20～100 m 之间，相比于参考-曲线调整范围约在-0.1～0.5 m之间，相比于参考-曲线调整范围在0～2.1 m之间；同时由图8（c）可以看出，优化后的-曲线的曲率范围在0～3 × 10m之间，曲率也相对较小，说明优化后的-曲线平滑性没有太大变化，且由车辆车速和曲率峰值可以计算得到车辆的侧向加速度不超过1.6 m/s，可满足车辆的侧向稳定性要求；由图8（d）、图8（e）可以看出，优化后的纵向车速和纵向加速度所在的范围分别为18～22 m/s和-1～2 m/s，由于障碍车辆的运动状态发生了较大变化，这里优化后的轨迹加速度变化也相对较大，但侧向加速度和纵向加速度仍在合理范围内，可以保证车辆的稳定行驶，优化后轨迹相比于参考轨迹舒适性有所降低，但避障风险由参考轨迹的4.5下降至3.7，避障风险大大降低，以使车辆具备较高的行驶安全性；结合图8（f）可以看出，整个换道过程中，车辆在实时调整相对于参考轨迹、本车道障碍和目标车道障碍三者之间的相对距离，以计算出最优的换道轨迹，使车辆相对于障碍车辆的碰撞风险最小且尽可能跟随参考轨迹以保证整个换道过程的平顺性。

5 结论

（1）所提出的换道避障轨迹规划方法，将轨迹规划降维分解成路径规划和速度规划，根据本车状态和多个采样点生成候选-曲线簇和候选-曲线簇，简化了规划难度，且考虑了多种换道可能。

（2）基于指数函数设计了一种障碍风险评价函数，并结合轨迹平顺性、利他性和行驶效率等构建了综合评价体系，选取出一对最优的-曲线和-曲线的组合作为参考轨迹。

（3）以参考轨迹为引导，利用障碍车辆与本车之间的风险关系设计了优化目标函数，并基于分段样条曲线对-曲线和-曲线进行实时优化，通过外点法求解得出最优轨迹，使每个优化周期都会得出一对最优的-曲线和-曲线的最优组合。

（4）结果表明，该算法同时对速度和路径进行规划在满足车辆稳定行驶的前提下，具有更好的平顺性和舒适性，且应对不同障碍车辆运动状态变化时具有较好的适应性和避障调整能力，且该算法中所涉及的障碍风险指标可与决策层进一步交互。