考虑预期功能安全的智能汽车自动紧急制动系统*

谈东奎，胡港君，朱 波，金 来，张 捷

（1.合肥工业大学汽车工程技术研究院，合肥 230009；2.安徽三联交通应用技术股份有限公司，合肥 230081；3.公安部交通管理科学研究所，道路交通安全公安部重点实验室，无锡 214151；4.合肥工业大学智能制造技术研究院，合肥 230051）

前言

传统的自动紧急制动系统一般基于安全距离模型进行避撞决策，但在实际道路中，由于场景的复杂性和自身系统性能受限，自动紧急制动系统依然可能发生失效而导致不安全事故发生，此类在系统内部组件并未发生故障的情况下由外部环境扰动、系统功能局限或人为误操作导致的安全问题被称为预期功能安全。智能汽车作为一个智能个体，内在的复杂性和不确定性决定了它的安全性分析重点不同于传统汽车的质量保障领域，而是非故障安全领域。预期功能安全技术为智能汽车在非故障情况下提供了安全保障，是当前国内外学者重点关注和研究对象。

Mirko在文献［4］中阐述了功能安全和预期功能安全之间的关系，John提出了预期功能安全风险评估框架，丰富和扩展了预期功能安全概念的内涵。BOCH 公司把预期功能安全用于ADAS 系统的开发过程，并利用故障树分析方法来分析DA/AD 系统，但故障树作为传统的安全分析方法，依然是基于可靠性理论分析安全性，无法涵盖预期功能安全领域问题。2011 年，Leveson提出的STPA 方法被开始用于分析汽车预期功能安全问题。Mahajan 等运用STPA对车道保持系统进行安全性分析，提出了系统改进的安全要求。陈君毅等基于STPA 提出了一种面向高等级自动驾驶决策系统的安全性开发方法，对泊车系统进行了系统改进。

上述有关预期功能安全的研究虽取得一定理论性进展，但在运用到ADAS 系统开发过程中依然存在以下不足：预期功能安全性在ADAS 系统开发中如何量化以保证车辆正常安全行驶的问题没有探讨；未能通过试验对比验证考虑预期功能安全的ADAS系统的有效性。

本文针对以上不足，在传统自动紧急制动系统的基础上考虑了预期功能安全，利用STPA对系统进行安全分析，得出了系统的预期功能安全要求。然后围绕感知盲区安全车速，建立车辆与盲区内潜在行人横穿马路的相遇运动学模型，计算出不碰撞行人最高车速，再加入感知盲区面积变化率、城市道路限速与最低车速等因素，综合考虑得出盲区最佳安全车速变化曲线模型，接着设计速度滑模控制器跟踪该速度，最后分别在CarSim 仿真平台和在环仿真台架上验证了该安全策略的有效性。

1 自动紧急制动系统安全分析

1.1 基于STPA的安全分析方法

对于智能汽车而言，与预期功能安全有关的风险，只从独立的组件出发设计系统需求是难以发现解决的。STPA 将重点从可靠性理论转移到系统理论并关注组件交互事故和组件故障，实现安全性和可靠性的分离，既能解决功能安全领域问题，又能处理预期功能安全领域问题。

STPA 将安全定义为一个控制问题，把危害归结为系统设计和运行缺少安全限制的原因，通过控制系统的行为来限制系统的安全。其安全分析流程主要分为4个步骤：

（1）明确系统的功能；

（2）建立系统控制结构；

（3）识别不安全控制行为，确定危险事件；

（4）分析危险事件发生的原因，提出安全要求。

1.2 自动紧急制动系统的安全分析

自动紧急制动系统的功能为减速避障，其输入为车辆当前速度与障碍物位置，输出为目标速度。利用STPA对其进行安全性分析，可以得到自动紧急制动系统的不安全控制行为及其不安全控制行为原因，见表1。前3种均为系统组件因故障而造成的危险，属于功能安全问题，最后一种是由于外部遮挡物的存在和传感器自身性能的限制而产生的感知盲区现象，属于预期功能安全问题。

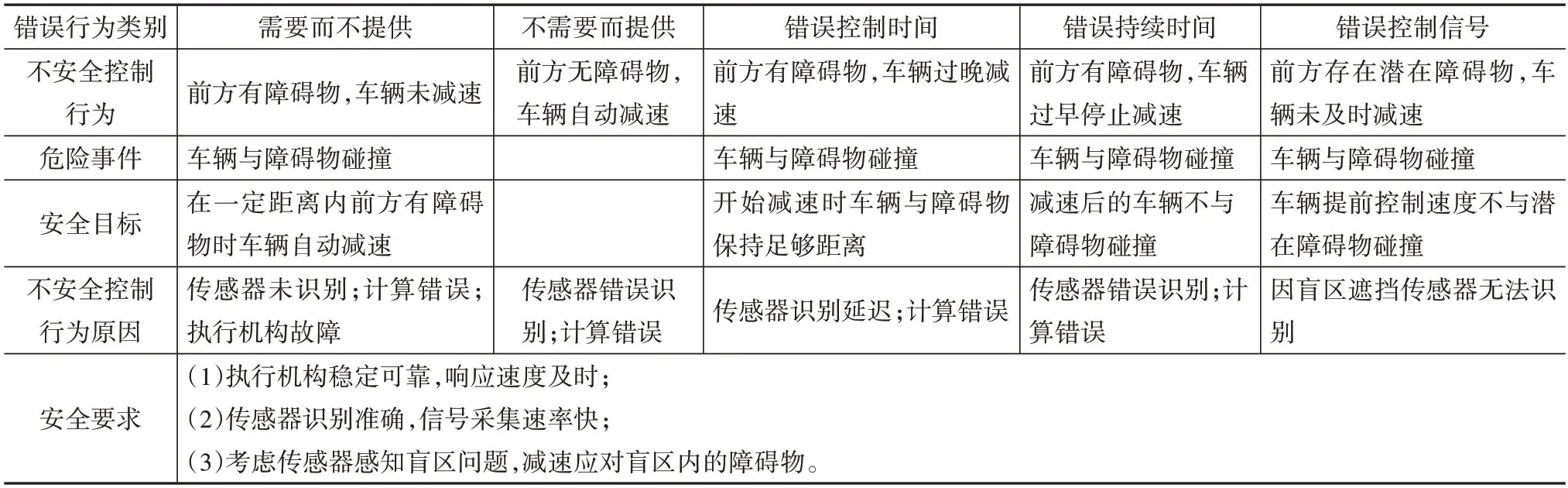
表1 自动紧急制动功能安全分析

安全分析结果表明要想解决感知盲区带来的预期功能安全问题，须在传统的自动紧急制动系统里加入感知盲区车速规划策略，提前减速来应对潜在的障碍物。

2 盲区场景下车辆安全车速决策

针对感知盲区现象，国内外多采用V2X 技术解决传感器性能不足的问题，但成本高昂，短时间难以实现。Yoshihara 等和Morales 等分别提出了基于Frenet 框架的安全驾驶模型和提取人类驾驶特征的强化学习模型，模拟专家驾驶员遇到盲区的行驶速度，但模型过于保守，极大影响车辆在盲区下的通行速度。袁朝春等将传感器感知盲区边缘线作为障碍物，根据边缘线的运动变化，建立安全距离模型避免车辆发生追尾事故，但没有考虑盲区下的人车相遇场景。

基于以上研究的不足，为对突然出现的行人进行安全避撞，考虑盲区对车辆的速度影响，寻求一个紧急制动前的车辆安全车速显得至关重要。

2.1 盲区场景下车辆-行人运动学模型

车辆在与盲区内的行人相遇前，为兼顾安全性和通过时长，车速应尽可能在避免碰撞行人的基础上保证更高；出于对行人发现车辆后可能做出加速向前奔跑的躲避行为的考虑，车辆应优先让行人通过。根据以上两点行车原则，可将车辆在盲区内的运动过程分为两个阶段：

（1）阶段1，车辆没有遇到盲区内行人，保持一个较高车速；

（2）阶段2，车辆感知到行人，进行紧急制动，最后在行人横穿轨迹线前停止，并建立以下模型，如图1所示。

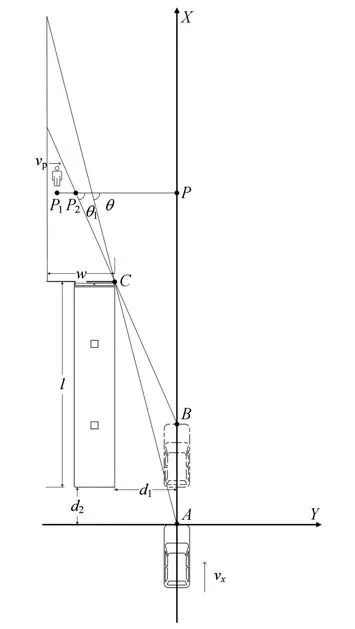
图1 盲区场景下车辆与行人相遇运动学模型

车辆从点匀速沿轴方向运动，同时盲区内处一行人匀速沿轴方向运动，时间后，车辆到达点，行人到达点，车辆传感器刚好检测到行人闯入，自动紧急制动系统触发，车辆以最大加速度紧急制动，在点处前停止运动。人-车相对关系有：

式中：v为车辆行驶速度；a为车辆制动减速度；为车辆从进入盲区到发现行人后经过时间；为行人与车辆的纵向距离。

根据正弦定理有：

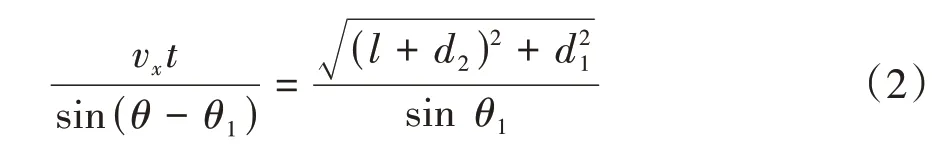
其中：

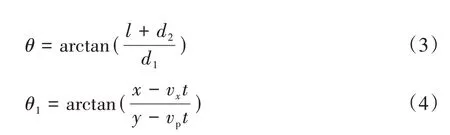
式中：为盲区纵向长度；为车辆传感器与盲区的横向距离；为车辆传感器与盲区的纵向距离；为行人速度，1.5 m/s；为行人与车辆的横向距离。

联立式（1）～式（4），可求得不碰撞行人最高车速为

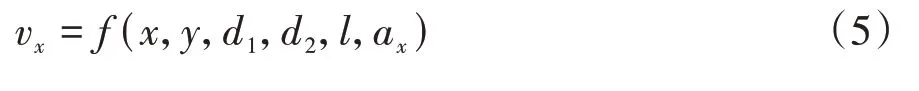
取=4.2 m，=30 m=10 m，a=4 m·s，在Matlab仿真计算得v=(，)，如图2所示。

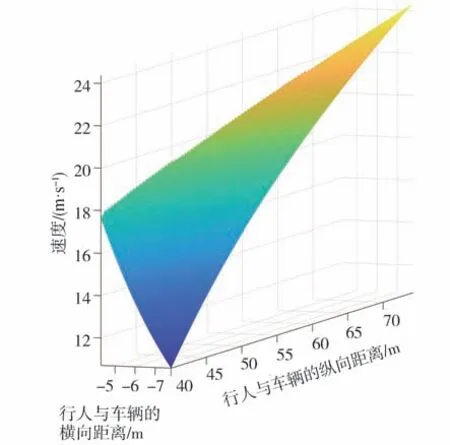
图2 车辆与盲区内行人不碰撞时对应的最高车速

2.2 最佳安全车速

2.1 节中求得的不碰撞行人最高车速是盲区安全车速考量的重要指标，但随着的减小，v也会逐渐减小，发生“死锁”现象。上述模型存在以下问题：

（1）没有考虑到盲区面积的大小，忽略盲区内行人的潜在概率；

（2）模型过于保守，将安全标准严格限制为车速降为零。

为解决上述问题，提高车辆通过盲区速度，利用不碰撞行人最高车速v、盲区面积变化率、城市道路限速与最低车速等因素综合计算盲区的安全车速，构建式（6），且≤。

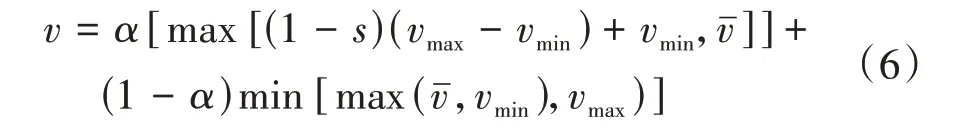
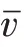
式中为盲区面积，=0.5(+)，为盲区宽度。

盲区面积变化率：

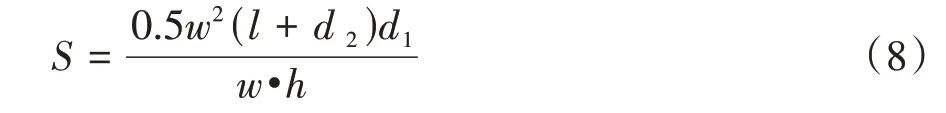
式中为预期功能起作用时的初始盲区长度，由式（9）得到。式（9）中40为车辆百公里制动距离，m。

最后调节求得最佳安全车速。

3 控制系统结构

所设计的控制系统主要由盲区紧急制动决策层、速度跟踪控制层、执行层和传感器组成，如图3所示。决策层根据车辆上的传感器不断检测周边盲区的信息，包括盲区纵向长度、车辆传感器与盲区的横向距离和车辆传感器与盲区的纵向距离，用于计算车辆的最佳安全车速，同时实时采集车辆当前行驶速度v、发动机转矩和制动力矩反馈给非线性观测器和速度控制器。控制层将决策层输出的车辆期望速度和目标加速度经过逆纵向动力学模型转换成期望油门开度和期望制动压力，利用切换控制器输出给执行层中的发动机和制动系统，以实现对期望速度的跟踪控制。

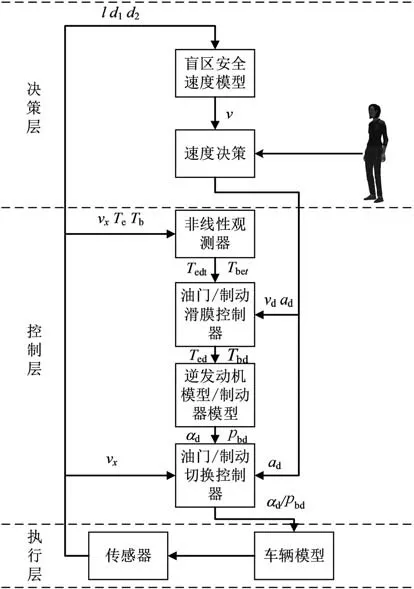
图3 考虑预期功能安全的智能汽车自动紧急制动系统结构

4 车速跟踪控制器设计

车辆本身是一个参数不确定的高度非线性系统，且容易受到外部干扰，本文在滑模控制器基础上加入了非线性干扰观测器，并设计了油门/制动切换控制器完成油门、制动器平稳切换，实现对期望安全车速的良好跟踪。

4.1 车辆纵向动力学模型

整车纵向动力学方程为

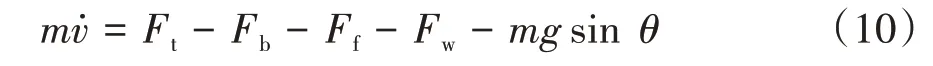
式中：为整车质量；为车速；为驱动力；为地面制动力；为滚动阻力，=sin；为空气阻力，=；为空气阻力系数；为重力加速度；为道路坡度；为滚动阻力系数。

车速与发动机转速的关系为

式中：为车轮半径；为发动机转速；为变速器传动比；为主减速器传动比。

发动机转矩与驱动力矩的关系为

式中：为发动机转动惯量；为发动机转矩；为驱动力矩。

联立式（10）～式（12）得

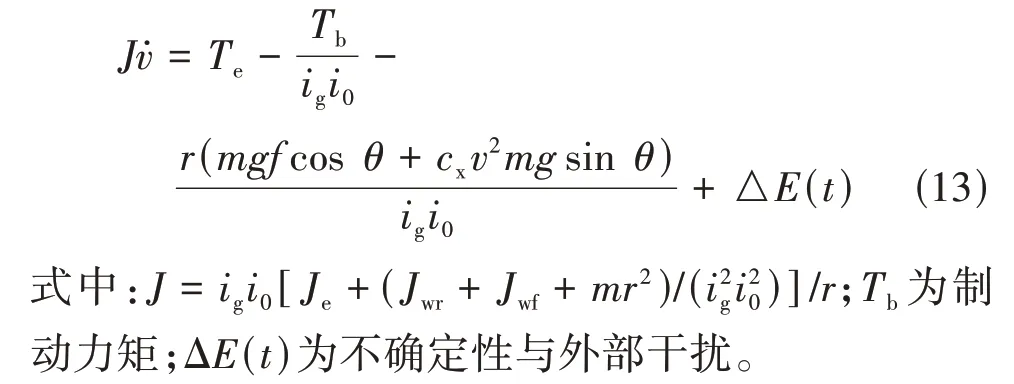
用等效1 阶惯性环节描述发动机和制动系的动态过程，发动机转矩与油门开度和制动力矩与制动压力之间的关系为

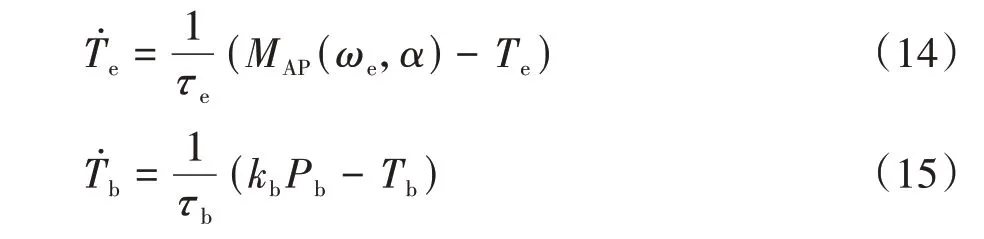
4.2 油门/制动滑模控制器

式（13）可改写为

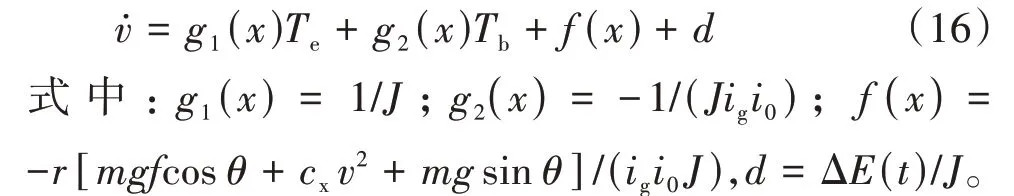
4.2.1 非线性干扰观测器

定义观测误差为

式中：、为滑模控制器的输出；、为非线性干扰观测器的输出。

4.2.2 油门滑模控制器

当采取油门控制时，制动力为0，由式（13）和式（22）得到加入非线性干扰观测器的车辆油门控制模型为

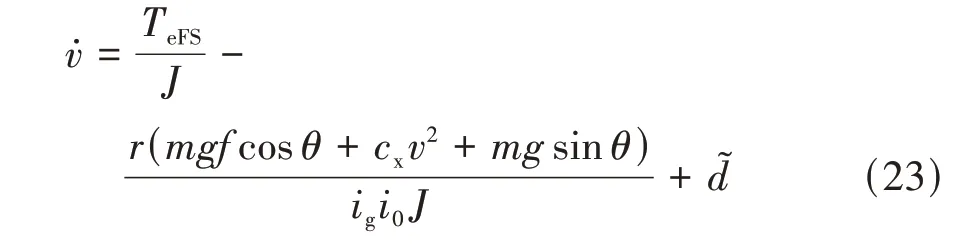
定义第1滑模面为

式中：为滑模面系数；=-。

要想达到理想的滑动模态控制，需满足：

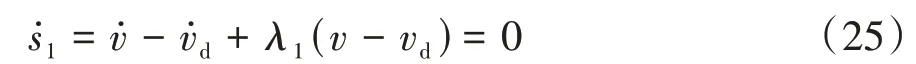
由式（23）和式（25）可得，发动机转矩等效控制律为

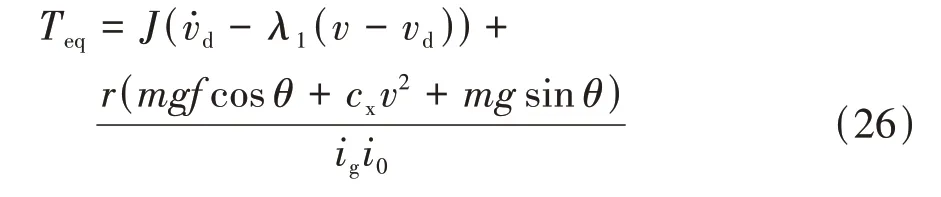
采用等速趋近率，滑模变结构控制律为

式中为反馈增益系数。

则发动机期望转矩为

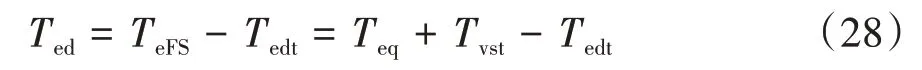
定义第2滑模面为

采用等速趋近率：

式中为反馈增益系数。

由式（14）、式（29）和式（30）得期望油门开度为

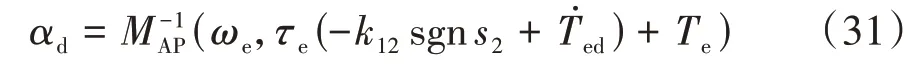
4.2.3 制动滑模控制器

当采取制动控制时，驱动力矩为0，由式（13）和式（22）得加入非线性干扰观测器的车辆制动控制模型为

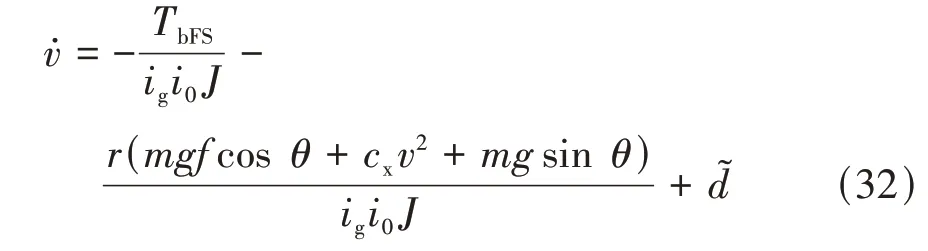
定义第3滑模面为

式中：为滑模面系数；=-。

要想达到理想的滑动模态控制，需满足：

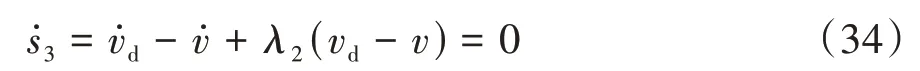
由式（32）和式（34）可得制动力矩等效控制律为

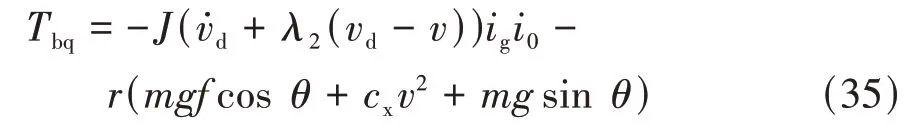
采用等速趋近率，滑模变结构控制律为

式中为反馈增益系数。

则制动期望力矩为

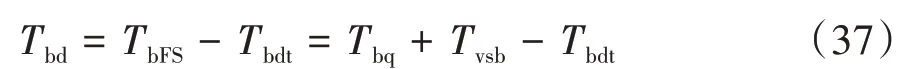
定义第4滑模面为

采用等速趋近率：

式中为反馈增益系数。

由式（15）、式（38）和式（39）得期望制动压力为

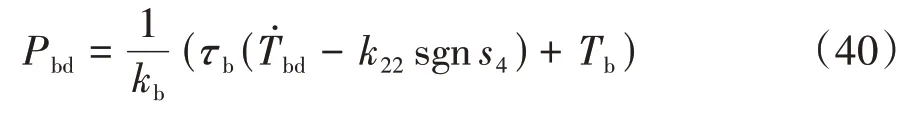
4.3 切换控制器

在进行车速跟踪时，需要油门和制动器联合控制实现。本文设计了节气门/制动控制切换时的加速度基准曲线：

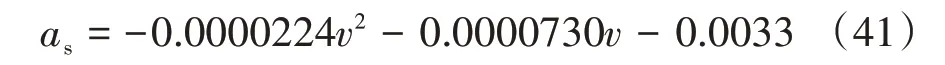
在基准加速度附近设置了切换门限，保证油门/制动较快响应的同时能平稳过渡，如表2所示。

表2 执行器切换策略

5 仿真验证与分析

5.1 感知盲区下最佳安全车速仿真

城市中大货车造成的盲区最为普遍，本文以此确定盲区仿真参数，如表3 所示，进行感知盲区下最佳安全车速仿真，取=0.6，结果如图4所示。

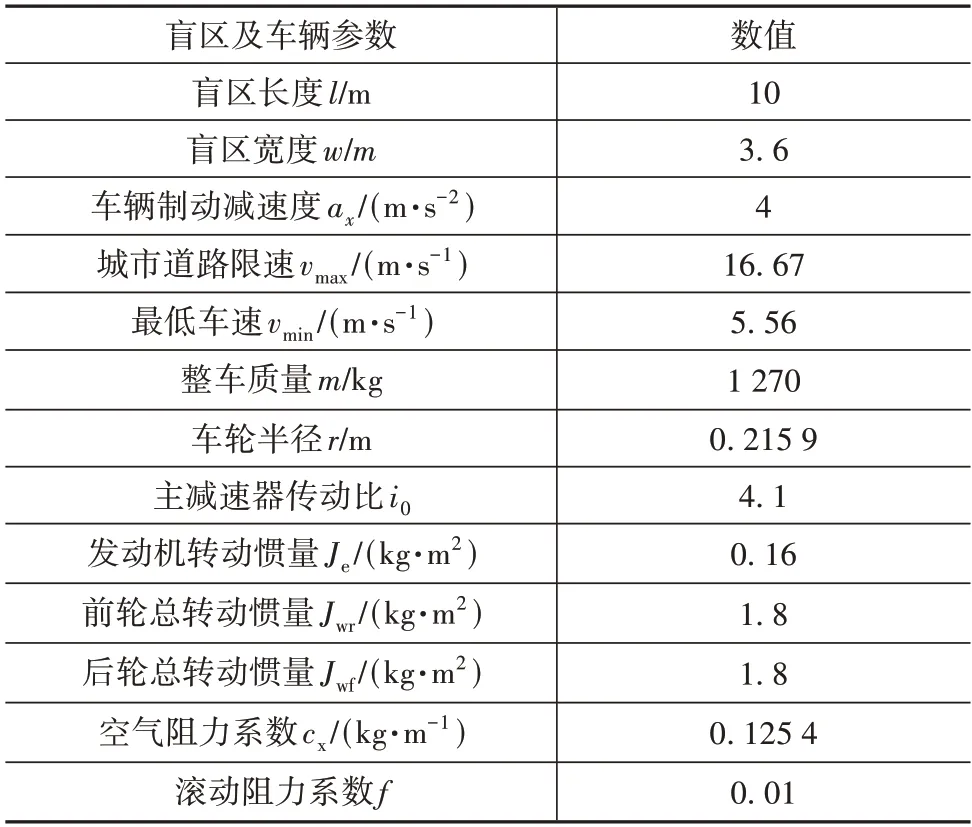
表3 仿真参数

由图4 可见，随着车辆传感器与盲区的纵向距离变化，感知盲区下车辆运动可分为4个过程：

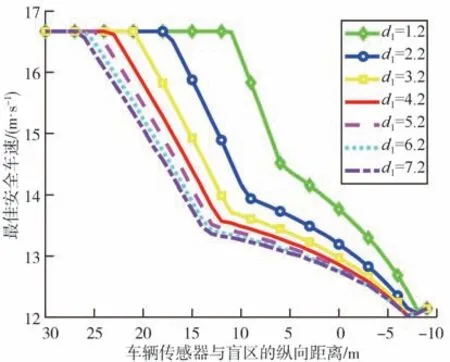
图4 感知盲区下最佳安全车速曲线

（1）匀速运动：车辆距盲区较远，盲区不影响车速；

（2）快减速运动：车辆进入盲区影响范围，车速快速下降；

（3）慢减速运动：车辆进入盲区一段距离，车速下降速率开始缓慢；

（4）加速运动：车辆快驶出盲区，加速离开。

随着传感器与盲区的横向距离的增大，车辆开始减速时刻会提前，车速变化也会趋缓。

5.2 感知盲区下车辆通过仿真

传统的自动紧急制动系统由于无法感知到盲区内的潜在行人，为规避行人碰撞风险，驾驶员在遇到盲区时会采取以下两种操作：

（1）在距离盲区一定距离时先匀减速；

（2）减速至通过盲区前达到安全车速后，保持匀速并通过盲区。

为验证基于感知盲区下最佳安全车速的自动紧急系统的有效性，设计如下两个试验，取=4.2。

试验1：为车辆设置3 种行驶策略，初始速度均设置为城市道路限速=16.67 m/s，并从同一地点出发。策略1：车辆按照盲区下最佳安全车速做减速运动；策略2：车辆以2.5 m/s减速度做匀减速运动减速至最低车速；策略3：车辆做匀速运动。车辆分别按照以上3种策略行驶，直至通过盲区。

试验2：车辆行驶策略、初始速度和出发地点保持不变，但在距离盲区消失30 m 时，盲区区域中线处有一行人在纵向距离盲区2 m 处以1.5 m/s 速度开始横向穿过道路，车辆在检测到行人后做紧急制动，直至停车。

5.3 仿真结果与分析

5.3.1 快速性

图5～图7为试验1下的仿真结果。

由图5 可知，车辆在策略1 下比在策略3 下行驶通过盲区的时刻只晚0.46 s，而车辆在策略2下比在策略3 下行驶通过盲区的时刻晚了1.76 s。由图6和图7 可知，车辆在策略1 下比在策略3 下行驶通过盲区时落后7.64 m，车辆在策略2 下却比在策略3下行驶通过盲区时落后了29.29 m。以上表明，按照感知盲区下最佳安全车速行驶的车辆虽然进行了减速操作，但在没有行人时能快速通过盲区。

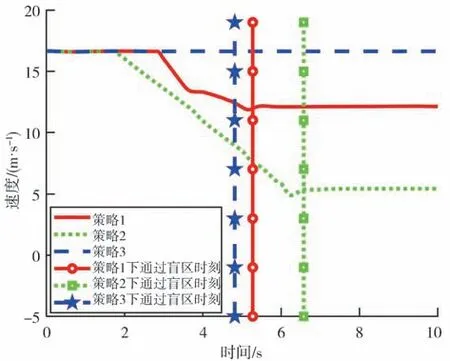
图5 盲区内无行人车速变化图

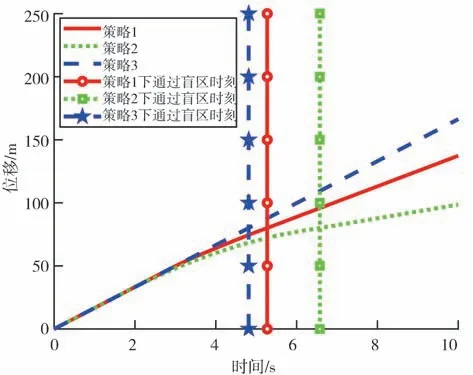
图6 盲区内无行人通过车辆位移变化图

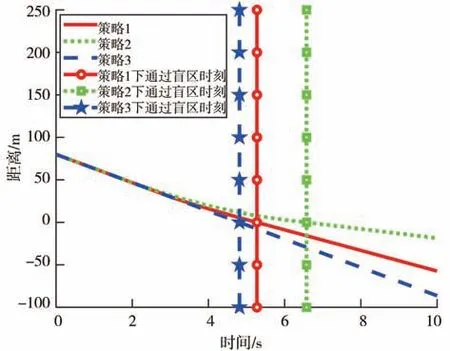
图7 盲区内无行人通过车辆与盲区消失界限距离变化图

5.3.2 安全性

图8～图10为试验2下的仿真结果。

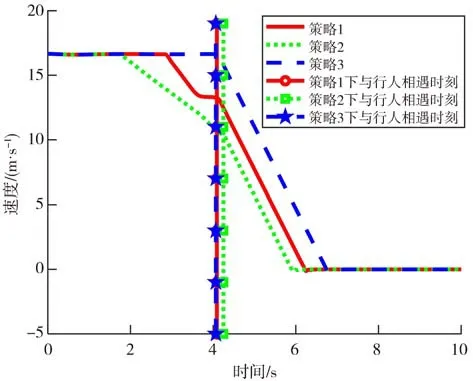
图8 盲区内有行人通过车速变化图

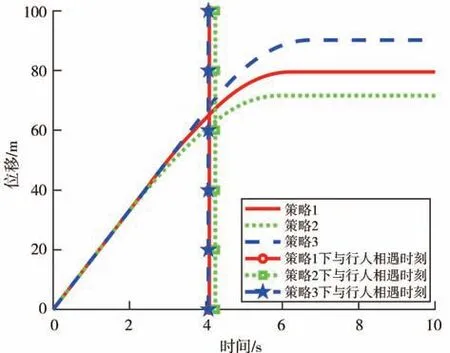
图9 盲区内有行人通过车辆位移变化图

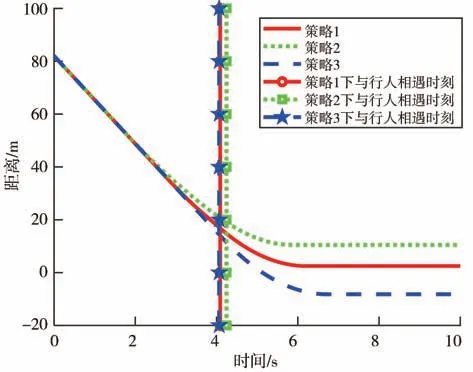
图10 盲区内有行人通过车辆与行人距离变化图

由图8可知，车辆在策略1、策略2和策略3下行驶分别在4.09、4.25、4.07 s后发现行人并进行紧急制动，且车辆分别在6.22、5.90、6.74 s 后速度降为零。由图9 可知，车辆在策略1 下比在策略3 下行驶发现行人时的位移少2.38 m，比在策略2 下行驶发现行人时的位移大2.26 m。

由图10 可知，车辆在策略3 下行驶越过了行人横穿轨迹8.21 m，对行人造成极大威胁，而车辆在策略1 与在策略2 下行驶都能在行人横穿马路的轨迹前及时停住车，保证行人的安全，且车辆在策略1行驶停车时仅仅与行人横穿轨迹距离为2.475 m，车辆在策略2 下行驶达到10.45 m。综上可知，车辆按感知盲区下最佳安全车速曲线行驶能有效利用盲区的长度，在尽量保证行人安全的前提下，快速通过盲区。

6 硬件在环仿真台架试验

为进一步验证该系统的有效性，搭建了硬件在环仿真台架，总体方案如图11所示。

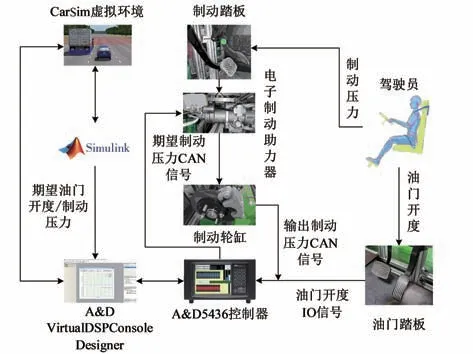
图11 仿真台架方案

试验3：驾驶员控制车辆以车速16.67 m/s 匀速驶入盲区，后自动紧急制动系统介入接管车辆进行制动减速，在距离盲区消失30 m 时，盲区区域中线处一行人在纵向距离盲区2 m 处以1.5 m/s 速度开始横向穿过道路，车辆在检测到行人后做紧急制动，直至停车。试验结果如图12～图15所示。

图12 和图13 表明该系统的硬件在环试验结果与仿真结果基本保持一致，车辆能按照最佳安全车速曲线变化行驶，并能在行人横穿轨迹前1.16 m 停车，保证了感知盲区下车辆行驶的安全性。

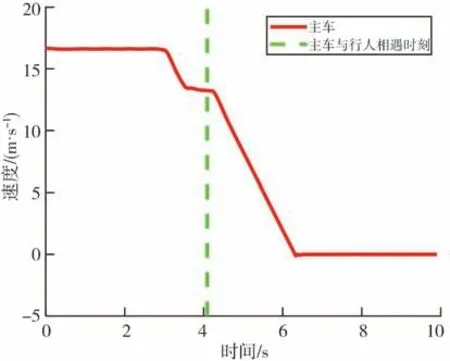
图12 速度变化图

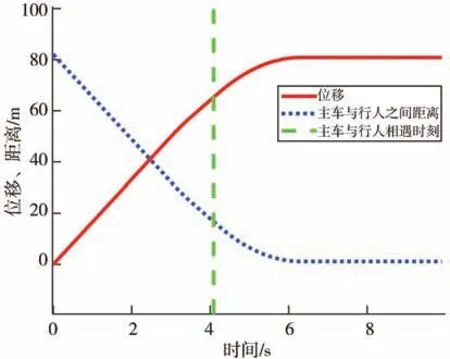
图13 位移、距离变化图

由图14 可知，线控制动系统的制动压力输出存在0.2 s的迟滞，最终导致车辆与行人横穿轨迹线距离较仿真结果缩短了1.315 m，但整体上对安全性影响较小。图15 显示在汽车遇到行人后车辆制动减速度短时间增加到0.74，超过了人体舒适加速度的极限值0.5，会让驾驶员有短暂不适的感觉。可以通过限制紧急制动最大制动压力来改善舒适性，但与此同时也会减低一定的安全性。

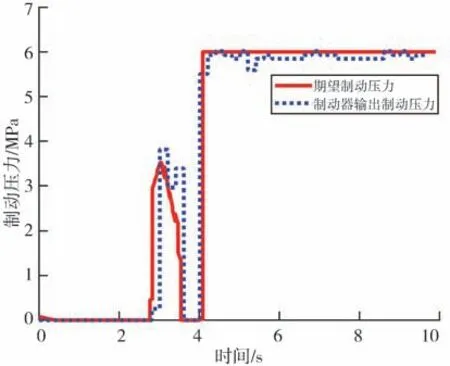
图14 制动压力变化图

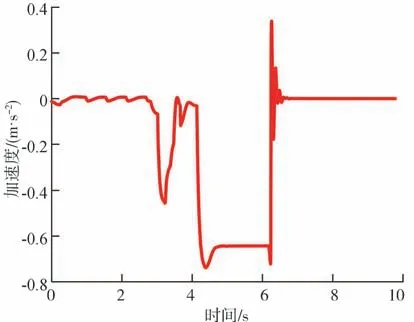
图15 主车加速度变化图

7 结论

（1）从考虑预期功能安全角度出发，在传统的自动紧急制动系统上增加感知盲区场景下安全车速规划，以保证感知盲区下车辆通过安全性；

（2）设计了基于非线性干扰观测器的速度滑模控制器，抵抗外部干扰和车辆本身的不确定性，精确地跟踪感知盲区场景下最佳安全车速；

（3）在CarSim 仿真平台上开展感知盲区内无行人通过与有行人通过两种试验，验证了该系统的快速性和安全性，最后搭建了硬件在环仿真台架，进一步验证了该制动系统的有效性。