基于Payne效应的膜式空气弹簧非线性动刚度模型*

邬明宇，陈志刚，童 浩，王 静，尹 航，郑文博，李 耀，禹 真，危银涛

（1.清华大学车辆与运载学院，北京 100084；2.中国第一汽车股份有限公司研发总院，长春 130013；3.汽车振动噪声与安全控制综合技术国家重点试验室，长春 130013；4.科马智能悬架技术（青岛）有限公司，青岛 266300）

前言

空气弹簧（简称空簧）以其优良的隔振性能，已在车辆和部分精密隔振领域得到了普遍关注和应用。对于乘用车来说，空气弹簧具有可调高度、改善平顺性、质量较轻和可有效抑制噪声等优点。普通乘用车单腔膜式空气弹簧通过管路连接到储气罐、压缩机或排气阀进行充放气操作。精确合理的空气弹簧动力学模型是空气悬架系统设计、建模和控制的基础。但是目前空簧动力学建模存在两个挑战：（1）气囊橡胶的贡献难以从理论和实验上验证；（2）动刚度随振幅的非线性变化难以建模。本文基于实验和理论分析，提出一个一般的非线性动刚度模型以解决这两个难题。

空气弹簧动力学等效模型在诸多论文中已有论述。Li 等利用几何学对铁路用空气弹簧进行非线性建模并通过实验分析了几何特性对垂向刚度的影响。Lee 等在Harris和Bryan工作的基础上，基于热力学建立双腔空气弹簧动力学模型并分析气体的振荡过程及其频率相关性。Docquire 等对动态过程中热交换过程的敏感性进行分析并研究了双腔空气弹簧内部的多变过程，其研究表明空气弹簧的动力学特性与热交换率呈强相关。李芾等对空气弹簧等效力学模型参数进行分析，给出不同参数对空气弹簧动力学特性的影响。陆晓黎等对空气弹簧进行有限元分析，从设计角度对空气弹簧的静刚度和承载力进行了精确预报。陈俊杰基于设计参数对车用空气弹簧的静刚度进行预测并分析了其振幅相关性，通过实验反推出橡胶气囊的影响。陈俊杰等利用线性模型和实验参数辨识方法对空气弹簧静刚度关键参数进行标定。

但上述研究都无法解决气囊橡胶对刚度的贡献度和动刚度随振幅非线性变化建模的难题，故本文中提出了一种考虑气囊橡胶Payne 效应和热力学等效刚度阻尼滞回特性的膜式空气弹簧非线性动刚度模型，以解决空气弹簧动刚度非线性建模难题。

橡胶材料的Payne 效应指的是橡胶材料动刚度随着简谐激励振幅的减小而增大的现象，有诸多学者对这一效应进行了广泛研究。本文中设计的动刚度实验定量表明，空气弹簧动刚度随振幅变化的非线性主要是由于气囊橡胶的Payne 效应引起的，这与Kind 等的定性分析一致，该文献指出膜式空气弹簧的Payne 效应是直接导致声振粗糙度（harshness）的原因。但是目前少见有基于Payne 效应、考虑气囊动力学特性进行膜式空气弹簧的动力学分析，并进行动刚度实部和虚部拟合及解释的方法和理论。本文中首先基于热力学考虑气体刚度、有效面积刚度和热交换等效阻尼和橡胶材料Payne效应理论给出一种解耦的膜式空气弹簧动刚度模型与各贡献量的数学表达与参数辨识方法；其次设计示功实验在不同激励频率和振幅下对其实部和虚部分别进行参数辨识，对动刚度模型进行验证；最后从振幅和频率两个维度给出各贡献量对动刚度的影响及其变化规律和物理解释。实验结果表明，本文提出的考虑Payne 效应的膜式空气弹簧动刚度模型在不同频率和振幅下均可精确反映动刚度的实部和虚部，为膜式空气弹簧的正向开发提供指导，并对膜式空气悬架的动力学行为的精确预报提供基础。

1 膜式空气弹簧动刚度模型

普通乘用车单腔膜式空气弹簧示意图及其参数定义如图1 所示，空气弹簧的垂向刚度主要受内部高压气体和橡胶气囊的影响。本文提出的膜式空气弹簧动刚度模型主要根据热力学和橡胶材料的Payne效应，分别对两部分刚度进行推导并得到最终的一般动刚度公式。其中热力学部分的推导，本文的作者已经在文献［22］中发表，但为了论文的完备性，本文仍简要给出热力学分析的部分。

1.1 热力学方程推导

首先考虑气体刚度。在充放气过程结束后，单腔膜式空气弹簧就成为了一个内部气体定质量工作的系统（见图1）。

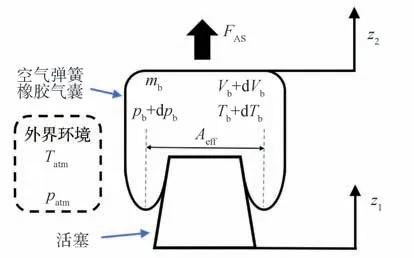
图1 单腔空气弹簧参数定义

首先假设力和位移矢量向上为正；压强、温度、体积和气体质量增大为正；系统从外部吸热、外部对气体做功和气体内能增加为正。表示有效面积。则基于热力学第一定律可以得出方程为

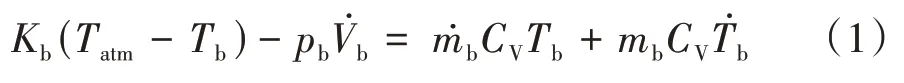
式中：下标b 和atm 分别代表气囊和外界大气；表示空气定容比热容；表示热交换系数。结合理想气体状态方程=和微分形式消去温度对时间的导数。又根据压强表达式和运动学方程，得到空气弹簧体积变化率和力学传递公式：

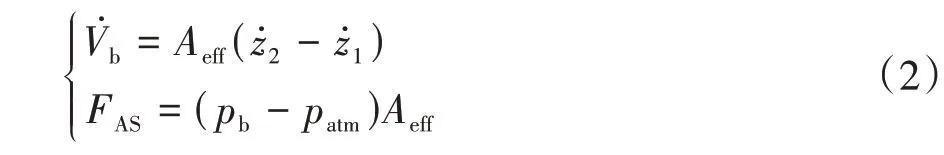
对气囊与外界大气温度差、气囊压强与其速度耦合项和空气悬架系统行程之间做了如下假设：

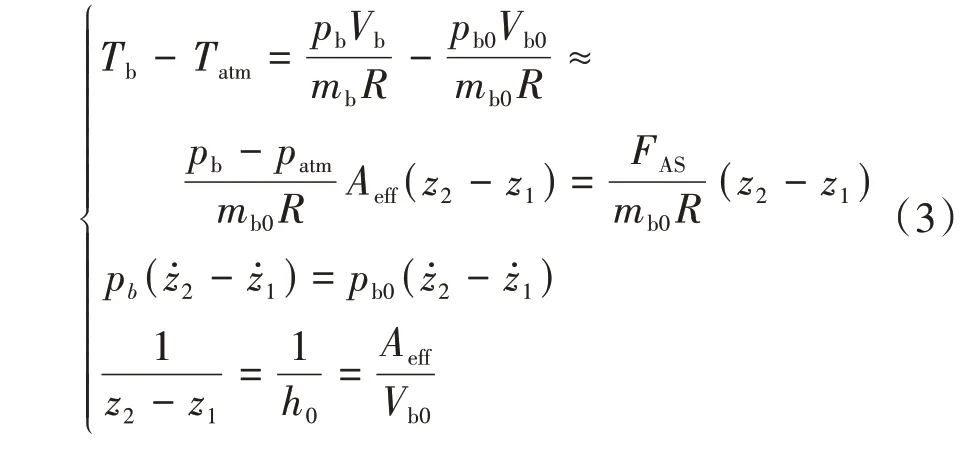
式中下标0 代表初始状态。对空气弹簧传递的力进行全微分，得到关于有效面积变化和压强变化的两部分对刚度的贡献量：

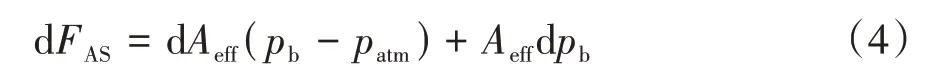
将式（2）～式（4）进行傅里叶变换，并将悬架动行程的傅里叶变换()=()-()代入，则空气弹簧气体产生的动刚度如式（5）所示。

式（5）即为由内部高压气体产生的单腔膜式空气弹簧动刚度公式，各部分具有明确的物理意义。表示由有效面积变化产生的刚度变化，基于实验测得；是由高压气体产生的刚度；是内部气体和气囊与外界热交换产生的等效阻尼。

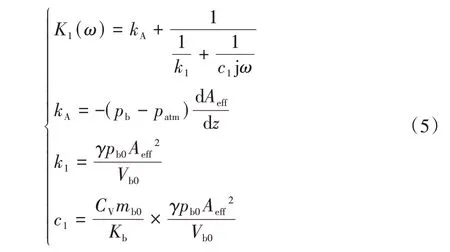
1.2 橡胶Payne效应刚度方程推导

膜式空气弹簧的气囊为橡胶-帘线增强复合材料，在对其垂向刚度计算时主要考虑橡胶动刚度的振幅相关性，即动刚度随振幅下降而急剧上升的Payne效应。为此，本文假设气囊结构动刚度随振幅的变化符合橡胶材料模量的动刚度随应变的变化规律，假设橡胶材料所受的振荡简谐应变为

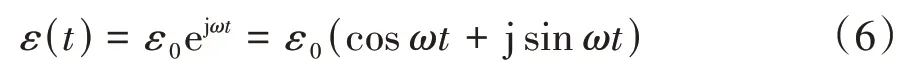
式中：为应变幅；为应变角速度。由于橡胶的黏弹性滞后效应，其复模量（动态模量）可以写为

式中为滞后角。进一步，可以将橡胶材料复模量分解成实部和虚部：

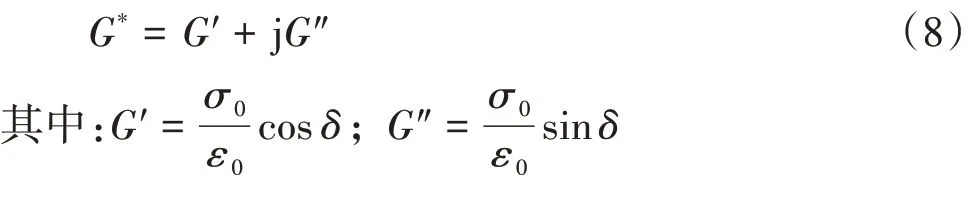
式中：实部称为储能（存储）模量，正比于每循环中单位材料所储存的最大能量；虚部″为损耗模量，表示循环中单位材料由于剪切和摩擦产生的不可逆能量损耗和黏滞损耗的热量。

填充橡胶的动态力学特性幅值相关性是由于填料网络间的van der Waals 键的断裂和重构引起的，且分别是应变幅的指数函数，Kraus假设每个动态循环内断裂的van der Waals 键的总数正比于现存的van der Waals 键总数，网络重构率正比于断裂的键总数，材料处于动态平衡时断裂和重构的速率相等。基于上述假设，则可以得到任意应变幅值下的动态损耗模量和存储模量，这就是著名的橡胶动态模量Kraus模型：

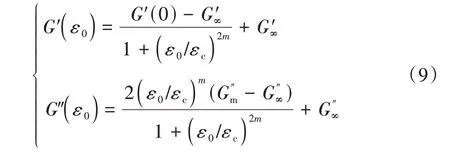
式中：为特征应变（定值）；为与炭黑结构的分维数相关的常数；′和″为无穷大应变下对应的模量。本文的一个创新点是认为空气弹簧动刚度的振幅非线性就是由于气囊橡胶的Payne 效应引起的，并且符合式（9）的物理规律，与式（5）热力学刚度公式结合，提出考虑空簧刚度振幅非线性和频率变化的普适的动刚度模型，并设计系统的动力学实验加以验证。由于膜式空气弹簧在进行示功实验时其宏观位移激励（动行程）幅值并非气囊的应变，假设气囊的应变与位移激励呈正比。进一步，结合橡胶材料的参数，大量实验分析结果表明的值约为0.5，且与炭黑种类无关，考虑实际物理意义与后续计算、参数辨识和实际工程应用等方面，取=0.5，代入式（9），可得空气弹簧气囊结构储能刚度和损耗刚度″与激励振幅关系，将其简化为

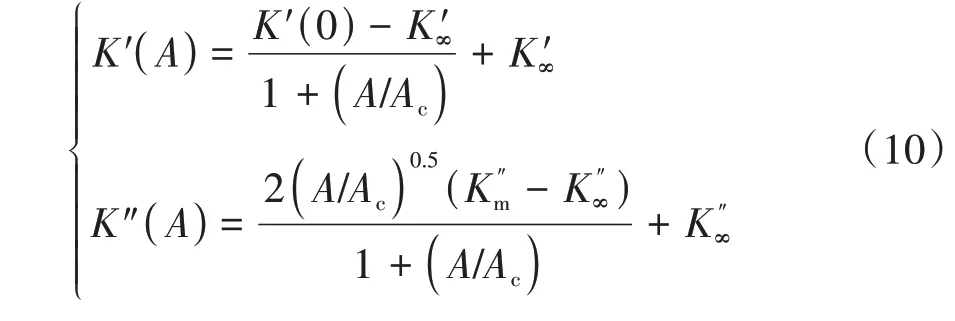
式中为特征振幅（定值）。基于前述模型，可得单腔膜式空气弹簧的动刚度计算方法（包含气体部分产生的动刚度和橡胶气囊产生的动刚度）：

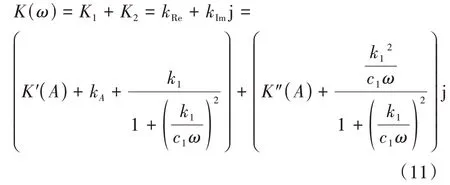
由此可见，膜式空气弹簧的动刚度分为实部（弹性刚度部分）和虚部（滞回损耗部分）。其中实部由橡胶材料刚度、有效面积变化率和气体等效刚度构成；虚部由橡胶材料滞回特性和固气间热交换产生。根据上述理论，可以得出膜式空气弹簧等效力学模型，如图2所示。

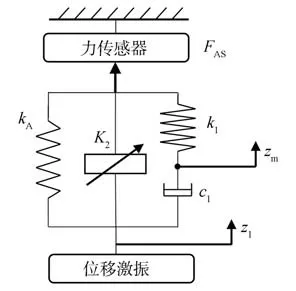
图2 单腔膜式空气弹簧等效力学模型

可以看出，单腔膜式空气弹簧等效力学模型的并联组成部分包括：有效面积变化产生的刚度、高压气体刚度与等效滞回阻尼串联、由橡胶材料产生的与位移相关的储能模量和损耗模量″。需要指出的是，橡胶材料的储能模量可以看做等效弹簧，但是损耗模量不能等效为线性黏性阻尼。虽然其形式上是直接对滞回特性产生影响，但其不随频率发生变化，仅是振幅的函数。

下面给出实验数据处理方法。对有效面积产生的刚度，参考式（5）理论公式，用最小二乘法进行实验数据计算。如上所述，空气弹簧由于滞回特性，其加载和卸载曲线不重合。假设其示功曲线如图3所示，取空气弹簧充放气结束后的静态工作点为基准点进行分析。

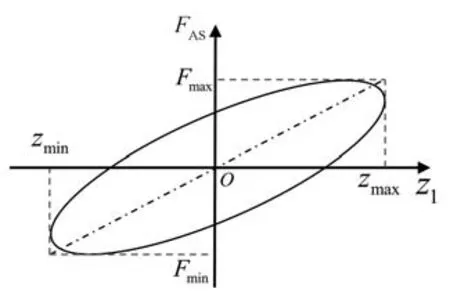
图3 空气弹簧（线性刚度）滞回曲线

根据滞回曲线的一般计算方法，可以列出关于实部和虚部的一般表达式为

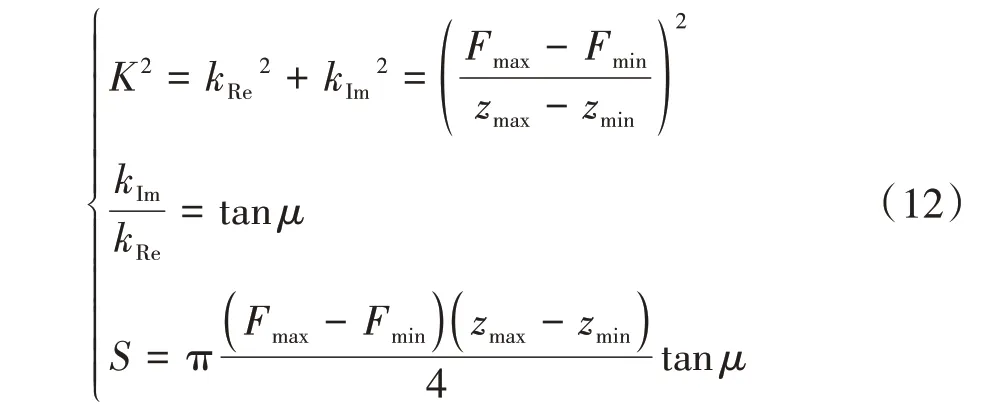
式中：为滞回角；为滞回面积。

基于实验值，通过式（5）和式（12）确定、k和动刚度实部与虚部，进而进行橡胶材料和热交换等效阻尼的参数辨识。下面根据实验进行上述参数的辨识并通过实验值和理论值的比较，验证本文提出的动刚度模型的合理性和正确性。

2 实验与模型验证

2.1 实验台搭建与实验描述

为验证本文中提出的动力学模型的合理性和准确性，本文采用国内某乘用车型后轴单腔膜式空气弹簧搭建了Mechanical Testing &Simulation（MTS）示功实验平台和气动系统。气动系统采用ϕ6 的高压管，并连接了减压阀和压强传感器（如图4所示）；作动器采用MTS 试验机液压正弦激励。利用减压阀控制空气弹簧内部气体压强并通过压强传感器读取绝对压强数值，调整完毕后对管长进行约束以减少由于管内气体带来的误差。在有效面积随高度变化的实验中固定压强为工作压强，改变工作高度（气囊上下端的距离，该距离为体积与有效面积的比值）进行工作高度范围内等分数据采集。示功实验中以空气弹簧初始工作状态（=0.23 m，=8 550 N）为初始状态进行实验分析。实验中选取的振幅和频率值如表1 所示，每个振幅下均进行所有频率的实验，每次实验进行3 个周期激励并取第3 组数据为实验值进行数据分析。

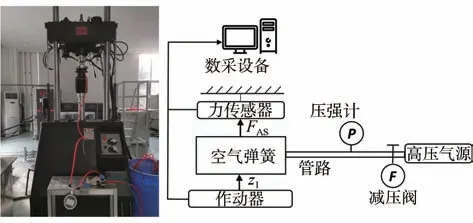
图4 实验平台与原理图

表1 实验振幅和频率

示功实验的初始状态参数如表2所示。其中温度、初始相对压强、初始压力由对应传感器直接测得；有效面积由初始位置处压力与相对压强比值计算。

2.2 参数辨识和模型验证

首先根据实验数据，利用式（12）计算出动刚度的实部和虚部。接着基于实验工况，利用式（5）和表2参数计算出气体产生的刚度和阻尼。然后利用最小二乘法进行橡胶材料Payne 效应相关参数的辨识。理论计算中所取辨识的参数结果如表3所示。

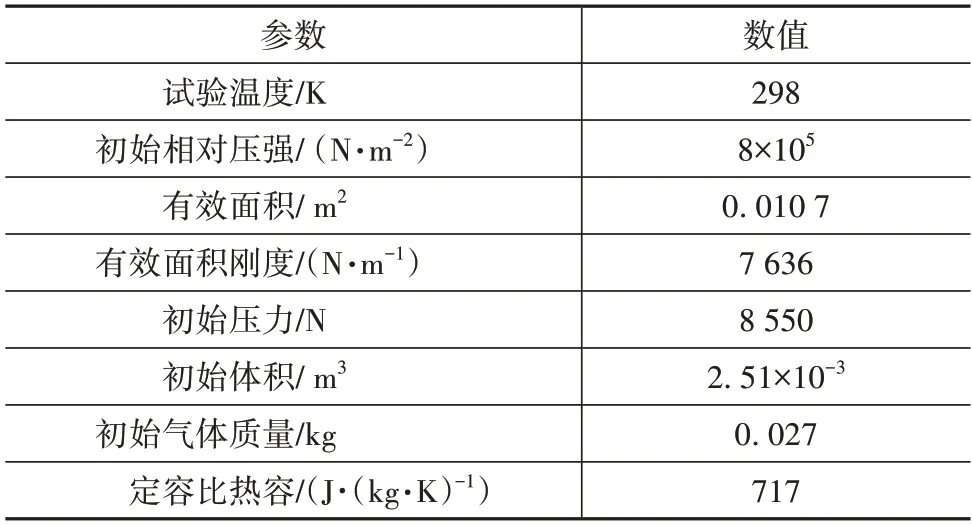
表2 示功实验初始状态及相关参数

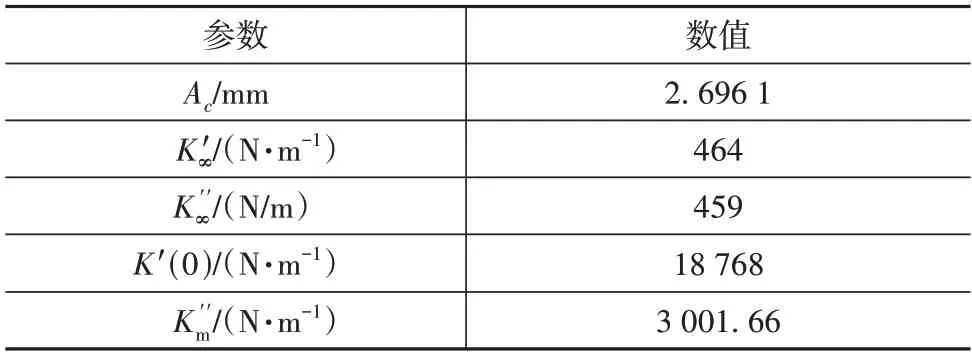
表3 参数辨识结果

后续进行气体相关参数辨识。根据物理变化，气体从低频到中频转换过程为多变过程。结合式（11）和表2 相关参数，可知气体热交换等效阻尼对动刚度实部的影响非常小，故根据不同频率下的动刚度实部平移关系，可以进行气体刚度的识别。同理，最后根据动刚度虚部平移关系和最小二乘法对等效阻尼进行识别。

对动刚度的实部对比结果如图5所示。从固定频率激励结果来看（单条曲线），低振幅下橡胶材料的动刚度实部增加尤其剧烈，即Payne 效应尤为显著。不同激励频率下的曲线呈现平移趋势，表明Payne 效应对频率变化不敏感，无耦合，验证了模型的准确性。从曲线簇随频率变化趋势可以看出，气体的等效阻尼对动刚度实部的影响会使其随频率增大而增大，且在1 Hz 激励频率以上差别不大，存在收敛特性。

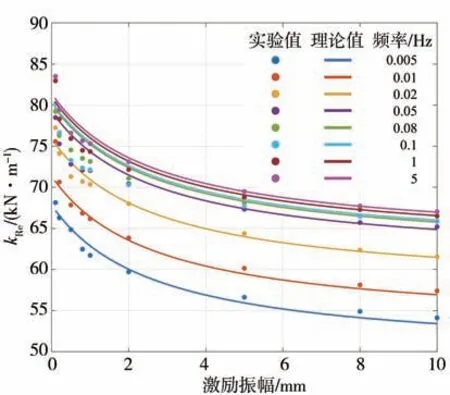
图5 动刚度实部对比结果

动刚度的虚部对比结果如图6所示。从单条曲线来看，在固定频率下由于橡胶材料的Payne 效应会使得动刚度虚部随振幅的增大呈现先升高后平缓下降的趋势。这一点从物理意义可以解释为：当振幅极低时材料的Payne 效应不明显，因为此时橡胶材料仍处于线弹性阶段；随着振幅增大，橡胶材料的弹塑性开始显现，van der Waals 键断裂程度迅速增大导致损耗模量的迅速上升。在超过一定振幅后每个动态循环时van der Waals 键破坏率趋于稳定，故呈现缓慢下降趋势。

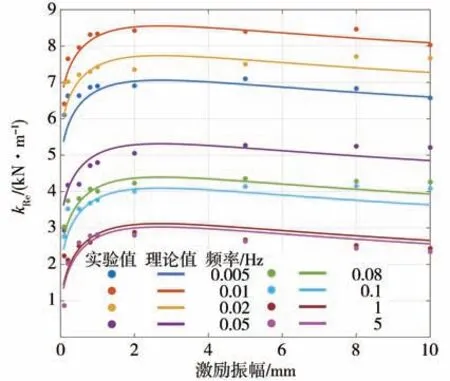
图6 动刚度虚部对比结果

从曲线簇变化趋势可以看出，随着频率增大，动刚度虚部急剧增大，到达峰值（频率约为0.01 Hz时）后逐渐减小的趋势。从物理意义角度解释为：在极低激励频率下气体呈现等温过程变化，加载卸载曲线重合（准静态）；在较高激励频率下气体呈现绝热变化，此时气体与外界热交换极不充分，能量损失极少，故也无热交换造成的滞回特性。最后给出不同频率下辨识的气体刚度对应的多变指数和等效阻尼，如图7 所示。其中多变指数由式（13）（源于式（5））和表2数据计算得出：

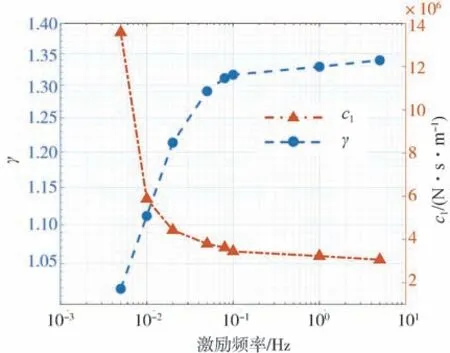
图7 多变指数与等效阻尼辨识结果

可以看出：气体刚度部分的等效多变指数随着激励频率增大而增大，表明气体从等温过程向绝热过程转变；由热交换产生的等效阻尼随着频率增大而减小，尤其在低频下变化尤为剧烈。这一现象的物理意义可以解释为：在极低频下根据式（11）可知，气体部分产生的动刚度趋向于由k+决定；在极高频下由于热交换不充分，故其动刚度仍趋向于由k+决定。但此时由于多变指数变化，导致实际动刚度增加。由气体产生的滞回特性也可由类似分析得出结论：随着频率从零增加，滞回特性先增大后减小。这与Kind等的定性分析一致。

基于上述实验和对比结果，引入气囊对膜式空气弹簧刚度贡献的新评价指标，其定义为在激励频率和振幅下由橡胶材料产生的动刚度模占总刚度模的百分比：

此值直观地反映了空气弹簧橡胶气囊对总刚度贡献的大小，权且称之气囊的刚度贡献率，对实际反映装配空气悬架系统的车辆在铺装路面上行驶的动态响应具有十分重要的作用，也可以直接作为评价气囊质量和动态特性的重要指标。本文选用的空气弹簧的气囊对总刚度的贡献率如图8所示。

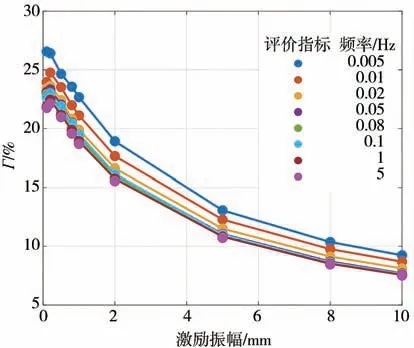
图8 气囊刚度贡献率随振幅和频率的变化

可以看出，空气弹簧气囊对总刚度的贡献率随着振幅增加而明显下降。根据表3 参数辨识结果也可知，当振幅进一步增大到无穷大时，该百分比将降低至1%以下。

3 结论

本文从物理机理出发，综合考虑膜式空气弹簧橡胶材料的Payne 效应、有效面积变化产生的刚度与气体刚度和等效阻尼对最终实验动刚度的影响。对实部和虚部分别进行参数辨识并从振幅和频率两个维度阐述了各因素对最终结果的影响，并给出了针对橡胶气囊的膜式空气弹簧新评价指标，结论如下。

（1）基于热力学和橡胶材料Payne 效应，提出了一种可以反映空气弹簧滞回特性解耦的动力学模型，明确各贡献量的物理意义和数学表达。

（2）证明了由橡胶材料的Payne 效应引起的动刚度增大在小振幅下不可忽视，实验和模型的吻合度验证了本文中的动刚度模型的准确性。

（3）从振幅和频率两个维度给出了各贡献量的变化趋势的物理解释。橡胶材料会使动刚度实部随振幅增大而减小，虚部随振幅增大呈现先急剧增大后逐渐减小的趋势；气体刚度和由热交换产生的等效阻尼使动刚度实部随频率升高逐渐增大且在大于约1 Hz 后变化不大，呈现极限特性，虚部随频率升高先急剧增大后减小。

（4）提出了反映橡胶气囊动刚度贡献率评价指标，该值随振幅增加明显下降，橡胶气囊在低振幅时产生的动刚度不可忽视。

本文提出的空气弹簧动刚度模型可为膜式空气弹簧的理论建模和正向开发提供指导。

附表1 正文中出现的参数及其定义