基于FPSC-FxLMS算法的车内发动机噪声主动控制*

贺岩松，蒋 昊，张志飞，周 桃

（1.重庆大学机械与运载工程学院，重庆 400030；2.重庆市埃库特科技有限责任公司，重庆 400000）

前言

主动噪声控制（active noise control，ANC）通过产生一个与目标噪声幅值相同、相位相反的声音，来达到降噪的效果。诸多研究已经表明ANC 对车内低频噪声有良好的消减效果，但仅仅降低噪声水平，特别是发动机噪声，往往并不能满足驾驶员的听觉感受，因此需要通过主动噪声均衡（active noise equalization，ANE）的方法来调整发动机噪声，以满足驾驶员对于发动机声音的期望。

Kuo 等在陷波FxLMS 系统的基础上引入增益因子来调节噪声中窄带分量的幅值，提出了ANE 系统，并在ANE系统中加入二级自适应滤波器构成滤波误差最小均方根（filtered-error least mean square，FELMS）系统，用以消除噪声中与参考信号无关的随机成分，实现主动声品质控制（active sound quality control，ASQC）。Wang 等将FELMS 算法与EMD 分解和频域块方法相结合，提出了HVA-EMDFELMS算法，在仿真中验证了该方法能对非稳态噪声的响度进行有效控制。为使ANE系统能有更快的收敛速度以适应发动机加速噪声的控制，de Oliveira等提出在ANE 系统上加入归一化滤波的NEX-LMS 系统，该系统能在缓慢加速时取得良好的控制效果。ANE系统虽然能实现噪声的消除、增强和衰减，但在增强模式下却对次级通路模型的准确性非常敏感，因此，Rees 和Elliott 提出Command-FxLMS 系统，它能实现与ANE 系统相同的功能且有更好的系统稳定性，并在该算法的基础上提出能发出更小次级声的PSC-FxLMS（phase scheduled command FxLMS）算法。由于PSC-FxLMS 算法需要对初级噪声的估计值进行傅里叶变换来提取相位，因此，次级通路的估计误差对其控制效果的影响较大，Patel 等提出MPSC-FxLMS（modified PSC-FxLMS）算法，在相位提取部分加入一种具有阈值参数的自适应滞后开关机制，使PSC-FxLMS系统获得了更好的稳定性。

在进行发动机噪声主动控制时，除了要求目标位置处的噪声达到预期的水平以外，还应该确保扬声器发出的次级声对其它位置没有过多的干扰，快速准确地提取初级噪声信号的相位是PSC-FxLMS算法能比Command-FxLMS 算法发出更小次级声的前提，但当前的相位提取方法并不能满足此要求，因此，本文针对PSC-FxLMS算法对次级通路估计偏差敏感的问题，提出改进的PSC-FxLMS 算法，并进一步提出FPSC-FxLMS（filter PSC-FxLMS）算法以解决改进PSC-FxLMS 算法中存在的傅里叶变换无法快速提取各频率相位的问题，通过Simulink仿真和某SUV 内基于DSP 控制系统的实车试验，验证了FPSC-FxLMS 算法能够在与Command-FxLMS算法达到相同控制效果的前提下，发出更小的次级声。

1 PSC-FxLMS算法

发动机噪声具有周期性，并包含有许多谐波分量，从频谱上看属于离散的窄带噪声，因此可以用自适应陷波算法进行消除。发动机各阶次噪声的频率f为

式中：为发动机噪声的阶次；为发动机转速。

自适应陷波算法利用声音在传播过程中的幅值和相位会改变、但频率不会改变的原理，提取发动机转速生成频率为f的参考信号x()，再经过自适应滤波以后生成频率为f的次级声y()，由此实现对发动机第阶噪声的消除。其原理框图如图1所示。

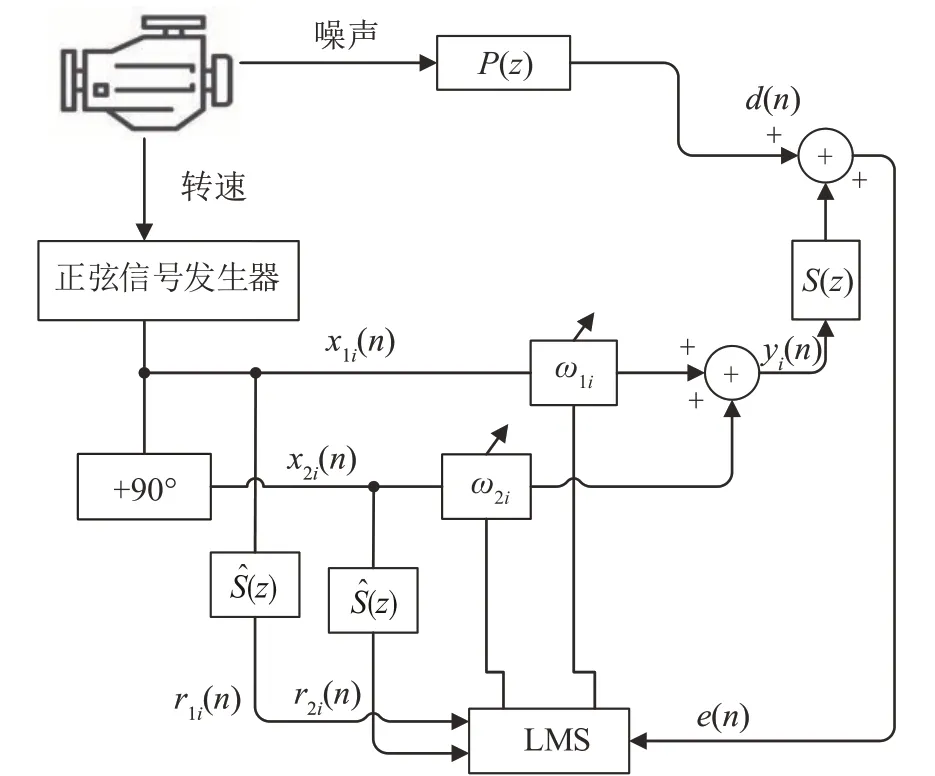
图1 自适应陷波滤波原理框图

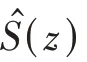
在对发动机噪声进行控制时，往往希望某些阶次得到增强，另一些阶次被衰减，以得到符合声品质控制目标的发动机噪声。Command-FxLMS 算法就可以使发动机噪声控制系统在收敛时，误差信号()中频率为f的分量达到某一特定值c()，而不是衰减为0。其原理框图如图2所示。

图2 Command-FxLMS原理框图

图中：c()为Command 信号；为增益系数；()为伪误差信号；()为实际误差信号。c()由参考信号生成：

伪误差信号()由误差信号()减去c()得到：

当系统收敛时，伪误差信号()中频率为f的分量等于0，()中频率为f的分量等于c()，此时：

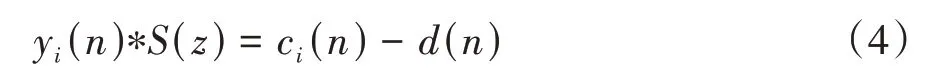
由于()由系统的外部条件决定，因此c()-()就决定了次级声y()的大小。令c()的初相位为ϕ，()中频率为f的分量初相位为ϕ，根据正弦信号的叠加原理，在增益相同的情况下，次级声大小与ϕ-ϕ的关系如图3 所示。可见，如果生成的Command 信号c()与()中频率为f的分量相位相同，即ϕ= ϕ，则y()的幅值最小，次级声源发出的声音最小；如果两者相位相差π，则y()的幅值最大，次级声源发出的声音最大。

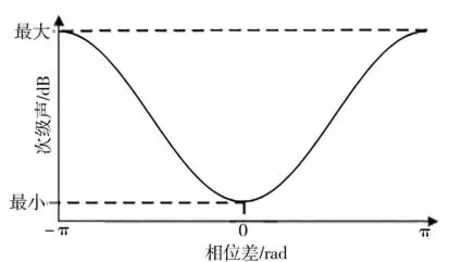
图3 次级声大小与相位差关系示意图

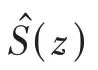
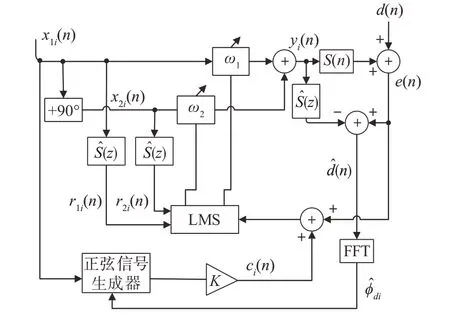
图4 PSC-FxLMS原理框图

式中：f为第阶次的频率；为采样频率。

2 FPSC-FxLMS算法

2.1 改进的PSC-FxLMS算法

初级噪声()中所包含的频率为f的噪声分量d()主要由发动机产生：

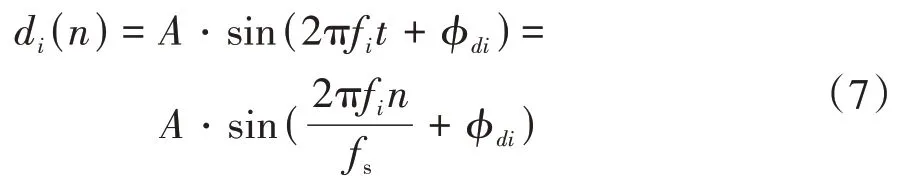
式中：为幅值；为采样频率；ϕ为()中频率为f的分量的初相位。

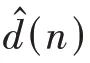
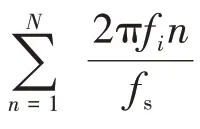
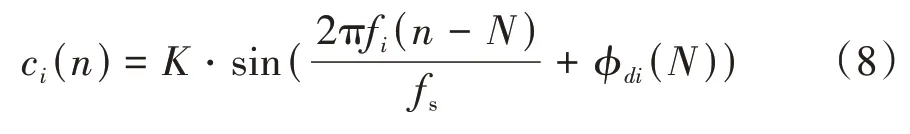
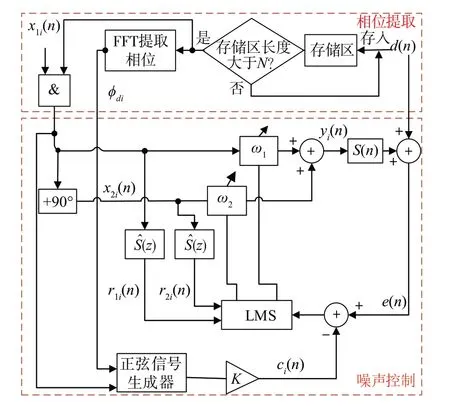
图5 改进的PSC-FxLMS算法原理图

为证明所提改进方法的有效性，将其与PSCFxLMS算法作仿真对比，对一发动机转速为3 000 r/min时的2 阶噪声进行控制，采样频率为2 000 Hz，将误差传声器处接收到的2 阶噪声幅值控制在0.002 V，在运行PSC-FxLMS 算法时，每200 个点，即0.1 s，提取一次相位。仿真结果如图6 所示。从图中可以看出，两种系统的控制效果基本没有差别，但改进的PSC-FxLMS 算法却只须提取一次相位信息，降低了算法的复杂度，且相位信息提取的准确性不会受到次级通路估计准确性的影响。

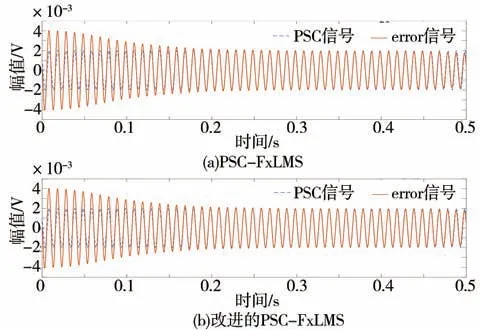
图6 两种系统的控制效果对比

2.2 FPSC-FxLMS算法

改进的PSC-FxLMS 算法虽然能消除次级通路估计误差所带来的影响，且通过减少相位提取的次数降低了计算复杂度，但基于傅里叶变换的相位提取方法存在采样时间与频率分辨率无法兼顾的问题，想要提高频率分辨率，就必须加长采样时间，采样时间与频率分辨率的关系为

以四缸发动机转速在1 575 r/min 时系统对2 阶发动机噪声进行控制为例，由式（1）可得发动机2 阶噪声的频率为52.5 Hz，此时要想利用傅里叶变换的方法提取出该阶噪声的初相位，频率分辨率至少应为0.1 Hz，因此采样时间应至少为10 s，无论是PSC-FxLMS 系统还是改进的PSC-FxLMS 系统，都在系统开启至少10 s 后才能得到c()，显然这不符合实时应用的要求。

因此，需要一种方法能够在各转速下，快速准确地得到特定阶次噪声的相位，以使Command 信号c()与频率为f的阶次噪声保持相位相同，本文中提出FPSC-FxLM 算法来满足上述要求，FPSCFxLMS 算法的噪声控制方法与改进的PSC-FxLMS算法相同，但它是利用FIR 滤波器和反三角函数来提取相位ϕ，其相位提取原理如图7所示，由此就可以直接得到第时刻噪声分量的相位ϕ()并用以生成Command信号c()。

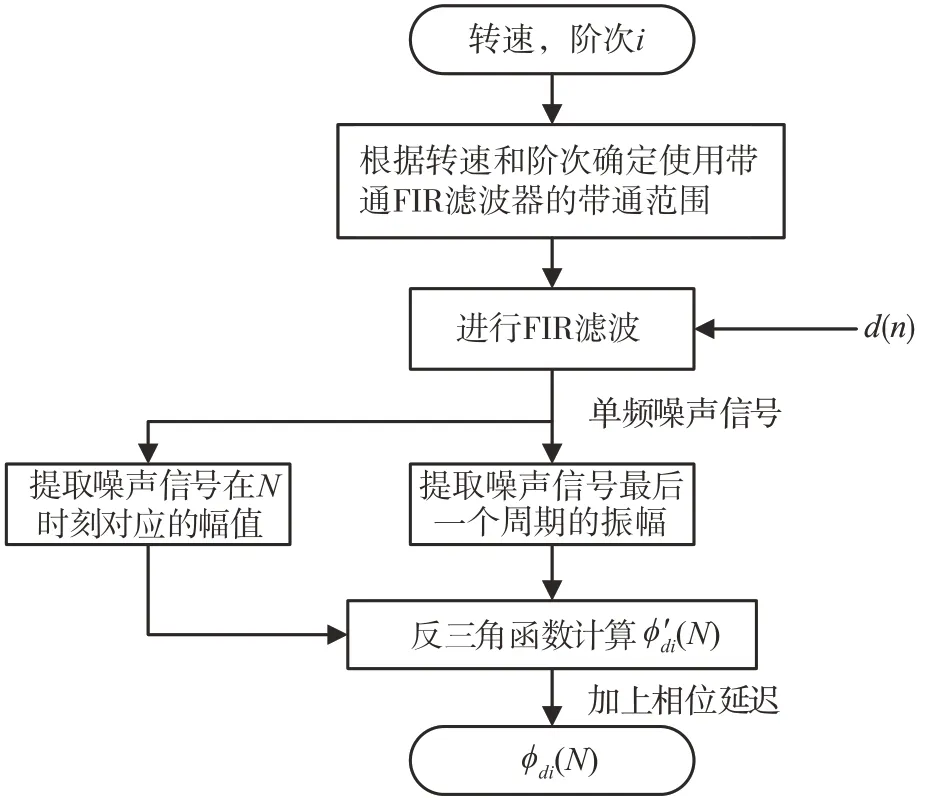
图7 FPSC-FxLMS算法相位提取原理图

FPSC-FxLM 算法的控制效果很大程度上取决于所选用的FIR 滤波器，因此，在设计FIR 带通滤波器时，应该保证所设计的滤波器能够将各个阶次噪声单独分离出来，发动机转速越低，发动机各阶次、半阶次噪声之间的频率越相近，所以FIR 滤波器应该具有较窄的带通范围，但当带通范围变窄时，想要在截止频率处达到相同的衰减率，就必须使长度增加，导致计算量和相位延迟增大。例如，想要控制发动机在1 000 r/min以上的阶次噪声时，FIR滤波器的通带宽度至多为8 Hz，设计一个阶通带为29-37 Hz的带通FIR 滤波器就可以用来提取发动机转速为1 000 r/min时的2阶噪声，得到的滤波器幅频响应曲线如图8所示。

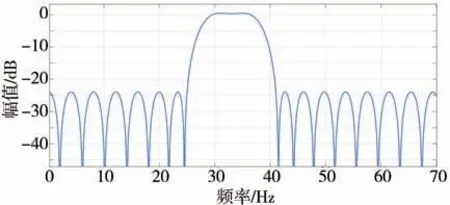
图8 FIR带通滤波器的幅频响应

除了关注FIR 滤波器的滤波范围以外，对初级噪声进行FIR 滤波也会导致相位延迟，但FIR 滤波相位延迟呈线性特性，如图9 所示，因此，可以通过根据阶次频率和所选用的FIR 滤波器阶数的不同来对FIR滤波器造成的相位延迟进行补偿。

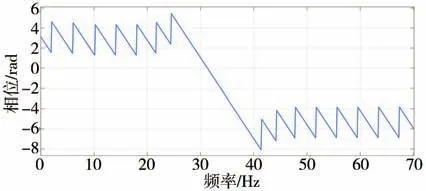
图9 FIR带通滤波器的相频响应

3 多通道FPSC-FxLMS算法仿真

为验证所提算法的有效性，分别搭建多通道FPSC-FxLMS 系统和Command-FxLMS 系统的Simulink 仿真模型，其中包括4 个扬声器和4 个传声器，模型中次级通路的估计值由附加随机噪声法得到。为使仿真更切合实际，采集某SUV 内扬声器到头枕位置处传声器之间的传递函数作为次级通路。主动噪声控制关心的是低频段的噪声，但由于扬声器的低频响应有限，因此依次让4 个扬声器发出50-500 Hz 的扫频信号，由误差传声器接收，由此得到4 × 4 个128 位的FIR 滤波器来模拟次级通路，如图10 所示。需要说明的是，为消除硬件设备所引入的干扰，该次级通路为电通路，即驱动扬声器发声的电信号到误差传声器接收到的电信号之间的通路。

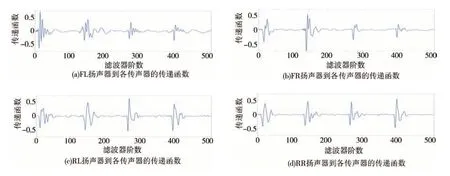
图10 仿真所用次级通路估计

仿真中以某SUV 空挡工况下转速为3 000 r/min时，位于左前（FL）、右前（FR）、左后（RL）、右后（RR）4 个座椅头枕处传声器测得的噪声信号为初级噪声信号，由转速计测得的转速信号用以生成参考信号，在多通道Command-FxLMS 系统和多通道PSCFxLMS 系统中，对2 阶发动机噪声进行消除、3 阶发动机噪声进行增强，4 个位置处的2 阶和3 阶噪声所设定的幅值如表1 所示。在系统收敛后，对仿真得到的误差传声器处的噪声信号和驱动扬声器的电压信号进行频谱分析，并将驱动电压信号的幅值进行对比，如图11、图12和表2所示。

表1 各位置的噪声控制目标幅值 V

结合图11、图12 和表2 可以看出，两个系统都能够将误差噪声控制在给定水平，但多通道PSCFxLMS 系统发出的次级声更小，说明该系统能够在保证达到与多通道Command-FxLMS 系统相同控制效果的前提下，发出更小的次级声，可减小对其它未进行噪声控制区域的干扰。

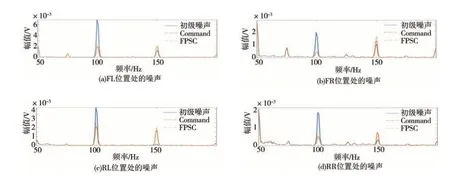
图11 4个位置处的误差信号频谱

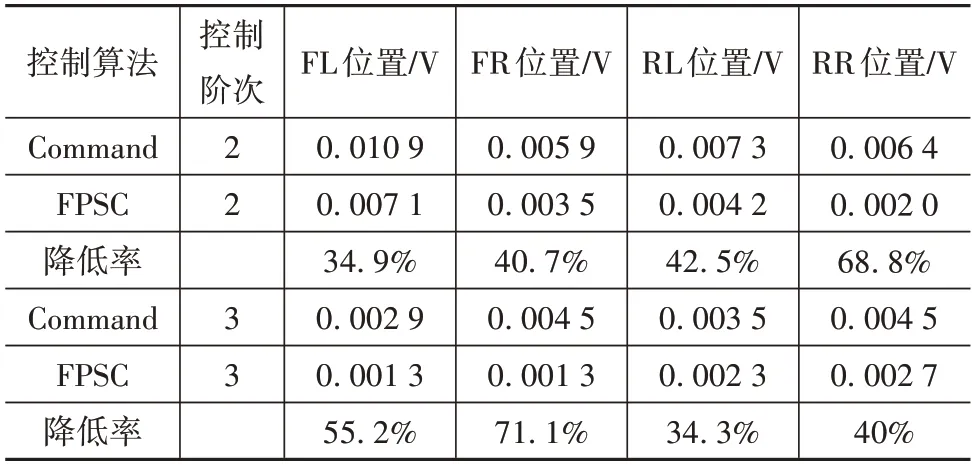
表2 各位置驱动扬声器的电压信号

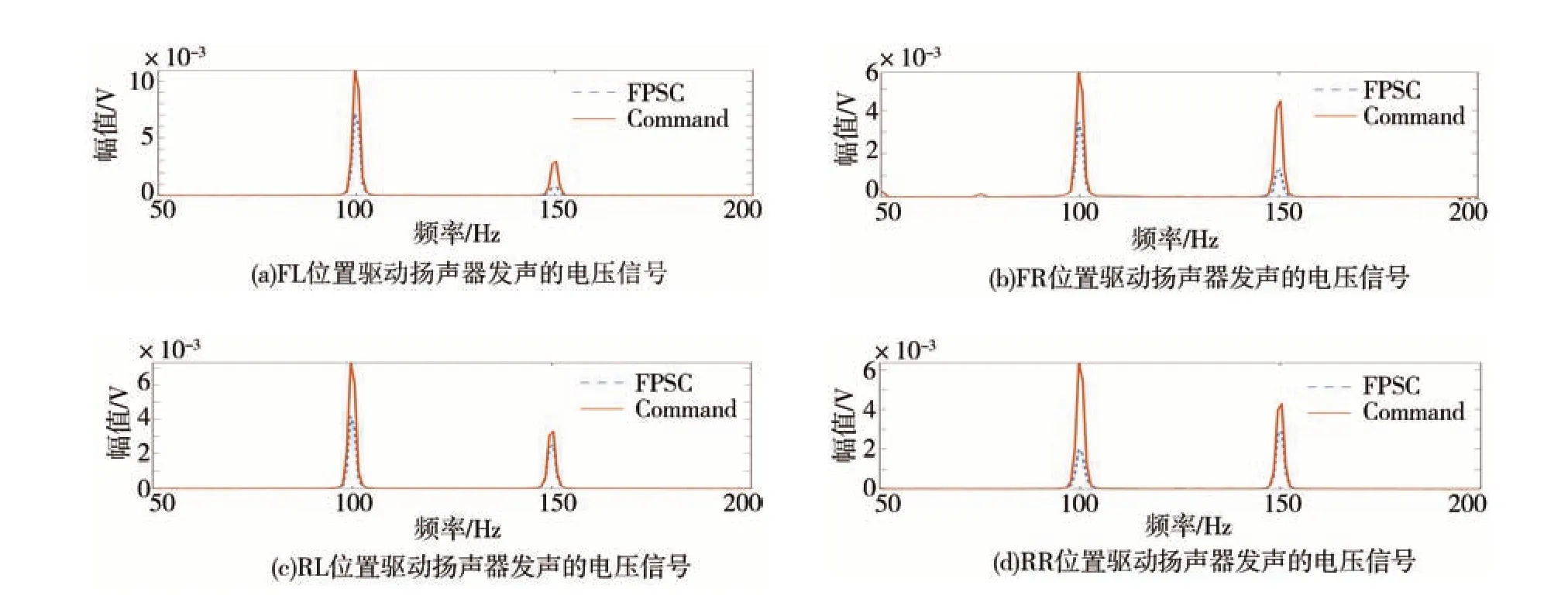
图12 4个位置处的次级声信号频谱

4 FPSC-FxLMS算法实车试验

4.1 试验概况

为进一步验证FPSC-FxLMS 算法在车辆运行过程中的控制效果，在另一辆配备四缸四冲程发动机的SUV 上进行试验，所需设备在表3 中列出。试验车如图13（a）所示，数字传声器位于座椅头枕下方，如图13（b）所示，头枕扬声器通过夹具固定在座椅头枕两侧，如图13（c）所示，DSP 与MCU、AD2428、数字功放都集成于一块PCB 电路板上，如图13（d）所示。

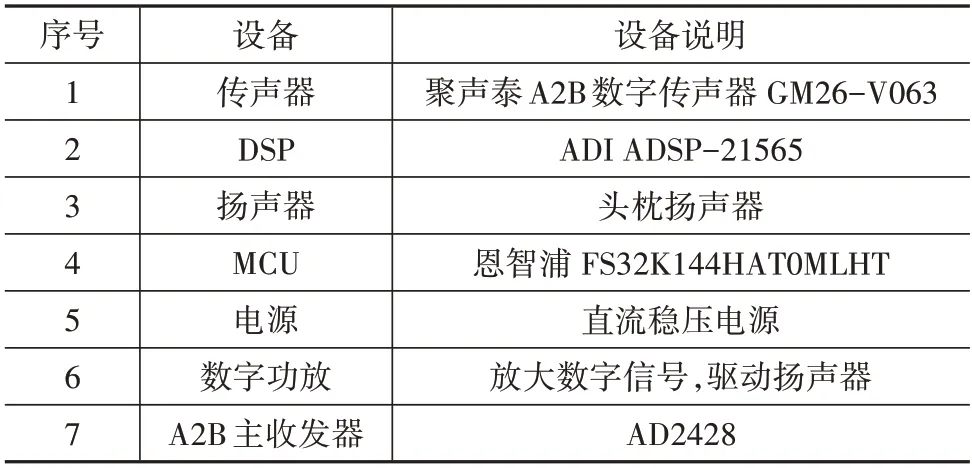
表3 设备说明

图13 试验所用部分设备

4.2 系统原理与试验过程

多通道FPSC-FxLMS 系统的原理框图如图14所示，MCU 解析CAN 信号并从中提取转速信号，上发给DSP 用以生成参考信号和选择带通滤波器，A2B 传声器接收到误差信号后，通过由主收发器AD2428和从收发器AD2426构成的A2B链路将误差信号上传至DSP，DSP 将传声器信号放入一个存储器中，当存储器达到一定长度以后，运行FPSCFxLMS 算法并生成次级声信号，该信号再经过数模转换和功放输出到扬声器，驱动扬声器发声。多通道Command-FxLMS 系统的原理框图与图14 相同，只是写入DSP的算法有所区别。

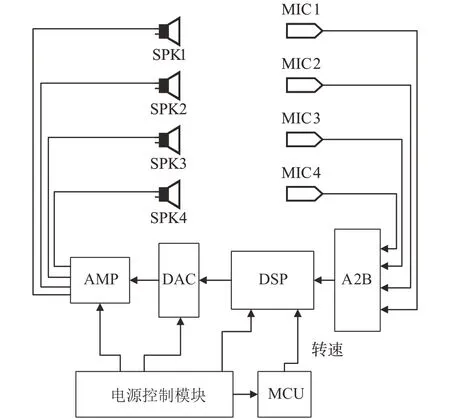
图14 硬件原理框图

为排除其它因素的干扰和保证多次试验的一致性，本次试验在周围环境安静的条件下进行，且该SUV处于原地稳速工况。在确认周围环境达到试验要求后，使发动机处于怠速800 r/min 工况和空挡1 900 r/min 工况，分别对驾驶员和驾驶员后排乘员的左右耳处这4 个位置的发动机4 阶和2 阶噪声进行控制，每个位置放置两个扬声器和传声器，分别位于头枕的两侧，如图13（b）和图13（c）所示，依次将这4 个位置命名为左前（FL）、右前（FR）、左后（RL）、右后（RR）。在发动机转速稳定后，保存多通道FPSC-FxLMS 系统和多通道Command-FxLMS 系统的误差传声器所收集到的数据和驱动扬声器发声的电压信号，验证当发动机处于不同转速时，FPSCFxLMS算法与Command-FxLMS 算法相比，能否在控制车内发动机阶次噪声达到相同水平的前提下，发出更小的次级声。

4.3 试验结果与分析

为了更明显地看出两种系统的噪声信号特点并验证初级噪声的前后一致性，采集两次降噪系统关闭时发动机在怠速800 r/min和空挡1 900 r/min下的噪声信号，进行傅里叶变换并得到其频谱，如图15和图16 所示。根据式（1）可得到怠速工况下的4 阶噪声频率为53.33 Hz，空挡1 900 r/min 工况下的2阶噪声频率为63.33 Hz，从图中可以看出，当发动机转速稳定时，初级噪声的前后一致性较好，并参考图中两转速下的初级噪声幅值，在Command-FxLMS系统和FPSC-FxLMS 系统中，将4 个传声器处接收到的发动机噪声目标幅值设置为表4中的值。

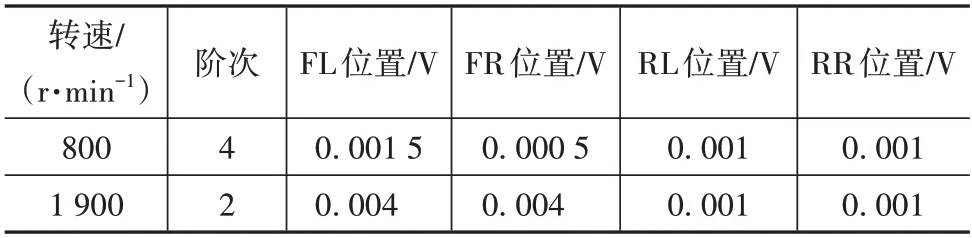
表4 各位置阶次噪声控制目标幅值

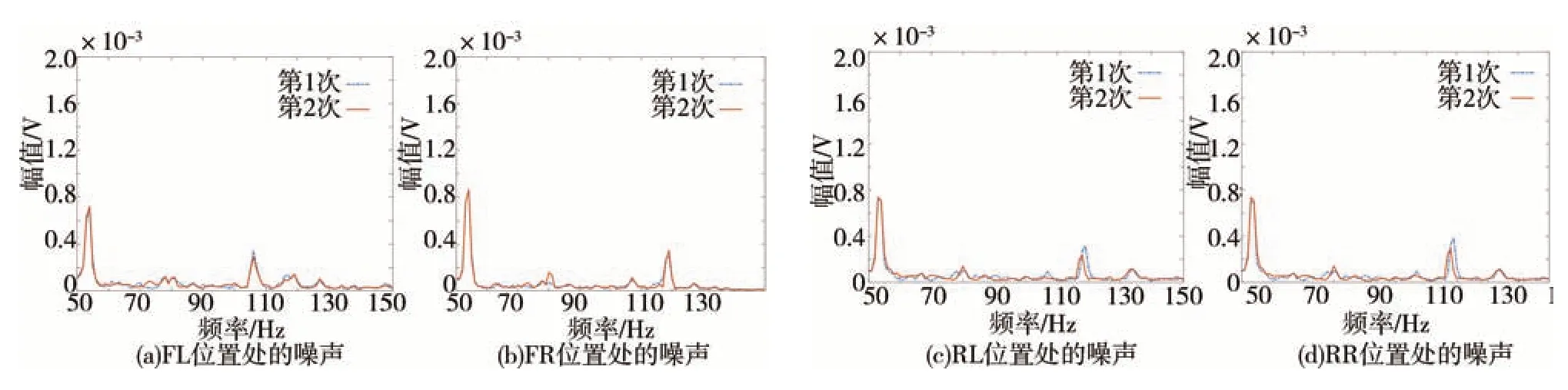
图15 800 r/min噪声频谱

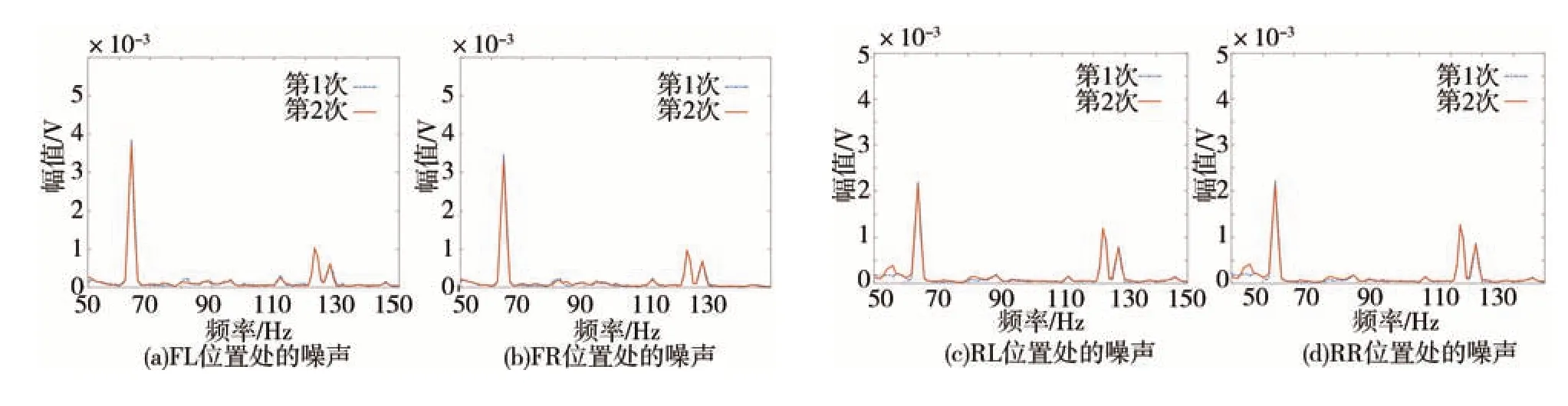
图16 1 900 r/min噪声频谱

在转速达到稳定以后，分别开启多通道Command-FxLMS 系统和多通道FPSC-FxLMS 系统。在系统开启后，DSP 自动同时储存5 s 的误差传声器电压信号和5 s 的驱动扬声器发出次级声的电压信号，在测试结束后，经由串口上发至PC 端。经计算得到在800 和1 900 r/min 转速下，两种系统分别开启时，误差传声器处的噪声信号和驱动扬声器电压信号的频谱，如图17～图20 所示。两系统得到的误差噪声信号幅值和电压信号幅值的对比如表5 和表6 所示。结合图17～图20 及表5 和表6 可以看出，无论发动机转速是在800 还是1 900 r/min，多通道Command-FxLMS 系统和多通道FPSC-FxLMS 系统都可以将发动机阶次噪声控制到给定幅值，但显然多通道FPSC-FxLMS系统驱动扬声器的电压信号更小，即发出的次级声更小。通过实车验证，说明所提出的多通道FPSC-FxLMS 系统能够在保证控制车内发动机噪声达到目标幅值的基础上，发出更小的次级声，减小对其他位置听音感受的干扰。

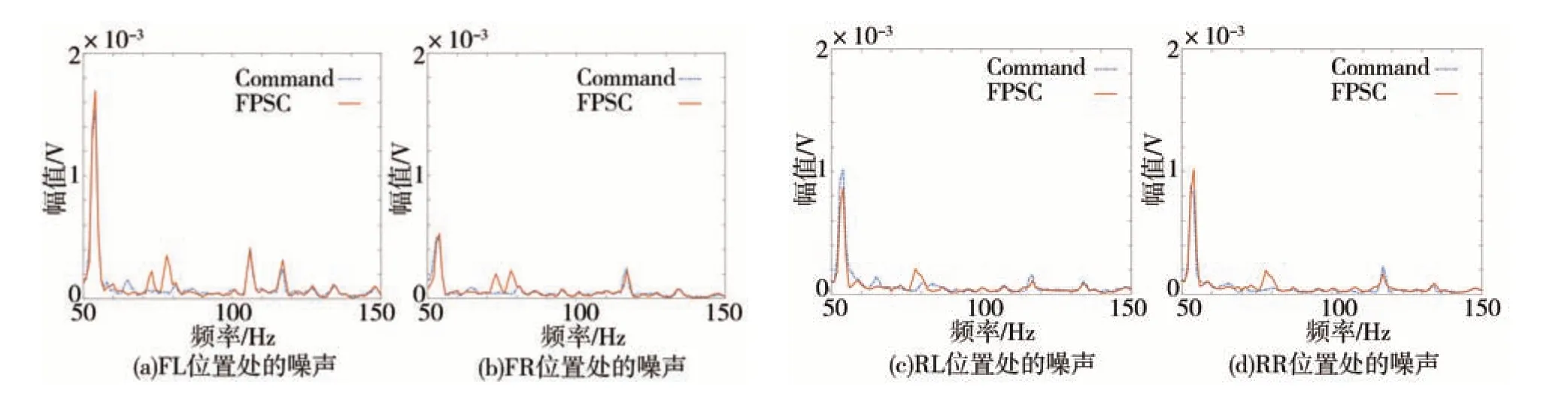
图17 800 r/min误差信号频谱

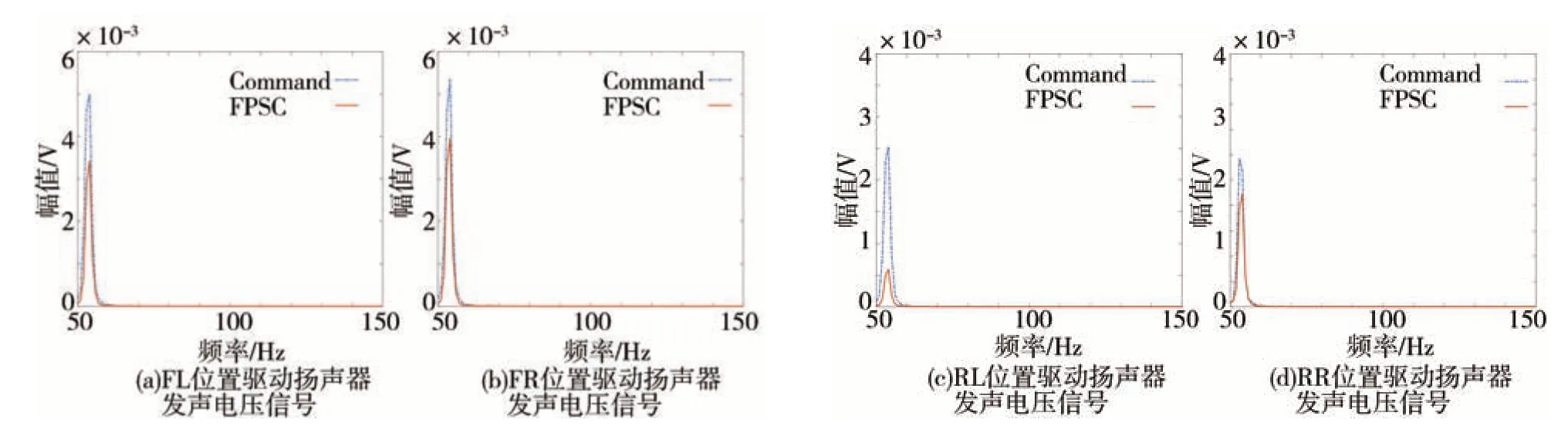
图18 800 r/min驱动扬声器电压信号频谱

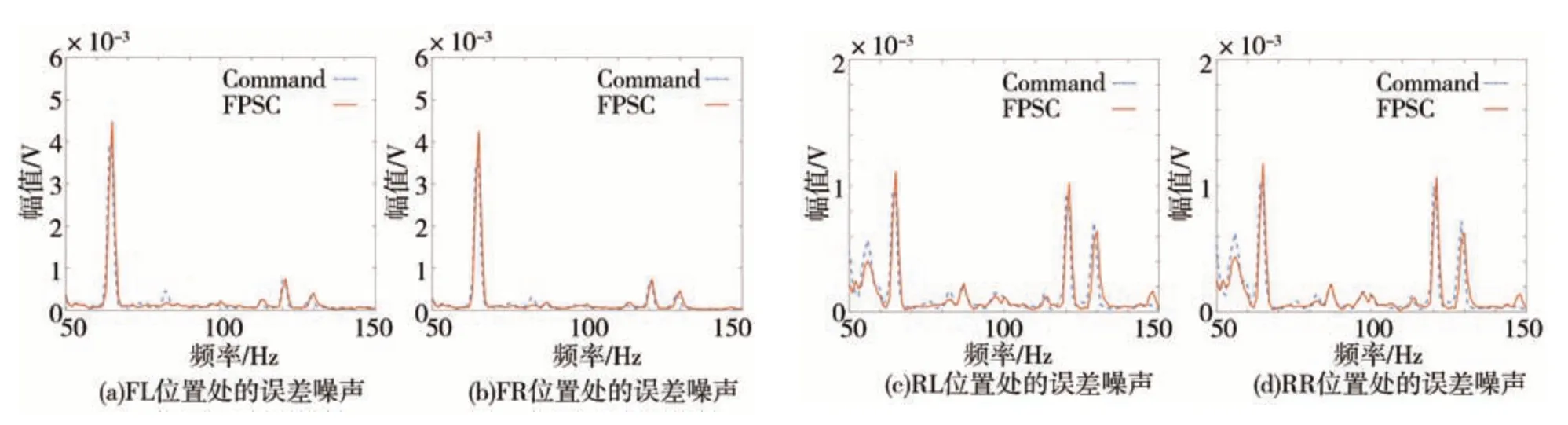
图19 1 900 r/min误差信号频谱

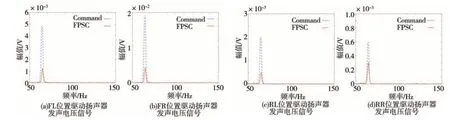
图20 1 900 r/min驱动扬声器电压信号频谱

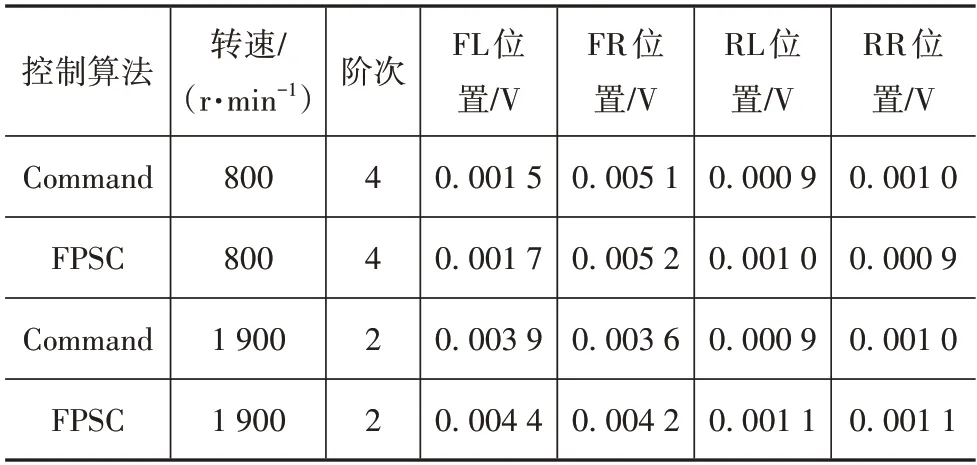
表5 控制后的阶次噪声幅值

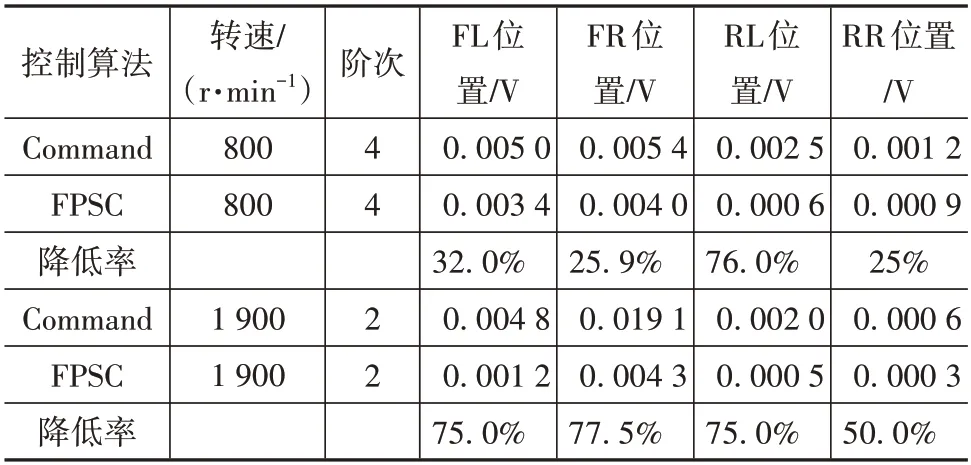
表6 驱动扬声器电压信号幅值

5 结论

（1）在PSC-FxLMS 算法的基础上提出了FPSCFxLMS 算法，通过将系统的相位提取和噪声控制模块进行分离，避免系统多次提取相位和次级通路估计不准确所带来的影响，利用FIR 滤波器和反三角函数提取初级噪声的相位信息，解决了FFT 提取相位所需时间过长的问题。

（2）基于某SUV 4 个座椅头枕位置处测得的噪声信号，建立多通道FPSC-FxLMS 系统和Command-FxLMS系统仿真模型。仿真结果显示，与Command-FxLMS算法相比，所提算法控制2和3阶噪声的次级声幅值降低34.3%以上。

（3）在另一辆SUV 上进行基于DSP 控制器的多通道FPSC-FxLMS 系统和Command-FxLMS 系统的实车对比试验。分别对800 r/min 怠速工况下的4 阶噪声和空挡1 900 r/min 转速的2 阶噪声进行控制，与Command-FxLMS 算法相比，所提算法在4 个位置上发出的次级声幅值降低25%以上。表明所提算法有效可行，能够在不同转速保持同样的控制效果情况下发出比Command-FxLMS算法更小的次级声。